Pemodelan seri waktu

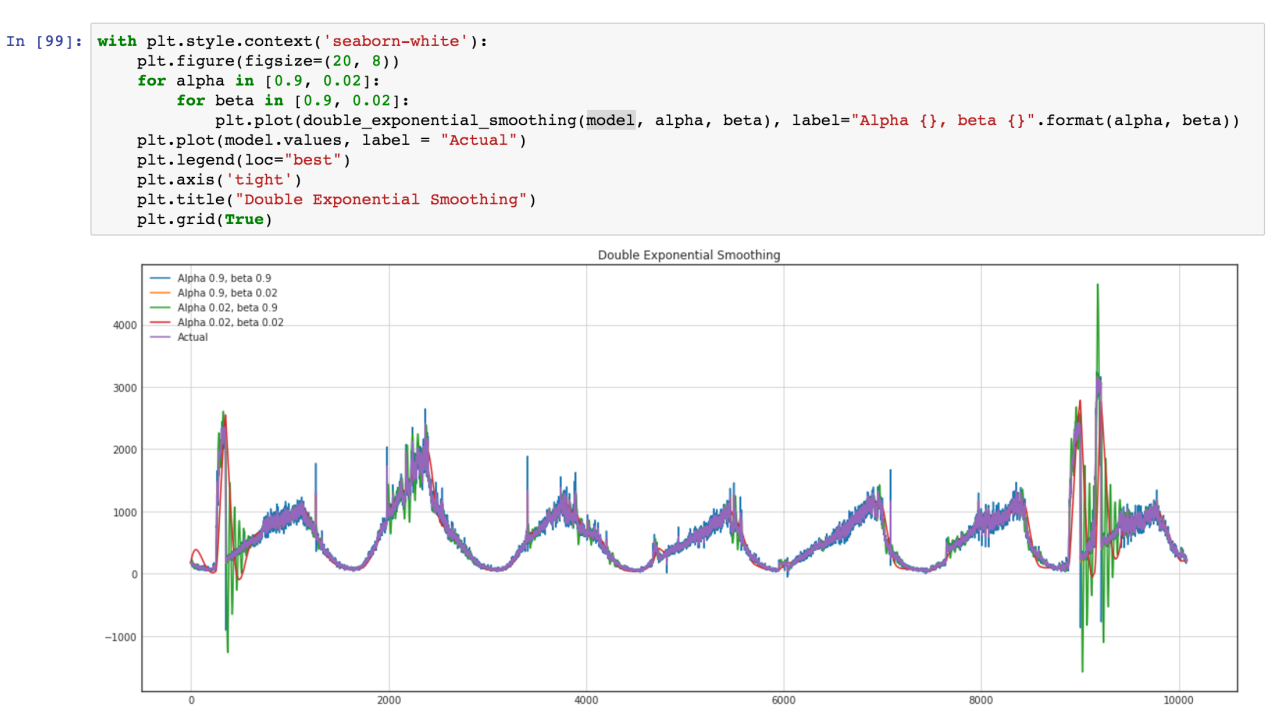
Ini adalah artikel pendek tentang memahami deret waktu dan karakteristik utama di balik itu.

Pernyataan problemm

Kami memiliki data deret waktu dengan keteraturan harian dan mingguan. Kami ingin menemukan cara bagaimana memodelkan data ini secara optimal.

Menganalisis deret waktu

Salah satu karakteristik penting dari deret waktu adalah stasioneritas.

Dalam matematika dan statistik, proses stasioner (alias proses stasioner yang ketat atau proses stasioner yang kuat) adalah proses stokastik yang distribusi probabilitas gabungannya tidak berubah ketika bergeser waktu.

Akibatnya, parameter seperti mean dan varians, jika ada, juga tidak berubah seiring waktu. Karena stasioneritas adalah asumsi yang mendasari banyak prosedur statistik yang digunakan dalam analisis deret waktu, data non-stasioner sering diubah menjadi stasioner.

Penyebab paling umum dari pelanggaran stasioneritas adalah tren dalam mean, yang bisa disebabkan oleh adanya unit root atau tren deterministik. Dalam kasus sebelumnya dari unit root, guncangan stokastik memiliki efek permanen dan prosesnya tidak berarti berbalik. Dalam kasus terakhir dari tren deterministik, proses ini disebut proses stasioner tren, dan guncangan stokastik hanya memiliki efek sementara yang berarti berbalik (yaitu, rata-rata kembali ke rata-rata jangka panjang, yang mengubah deterministik dari waktu ke waktu sesuai dengan tren).

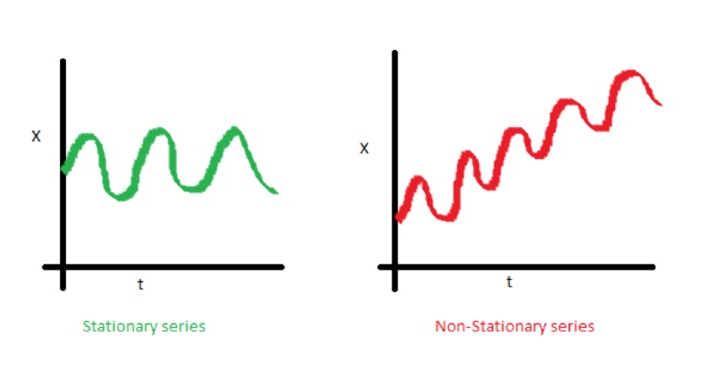
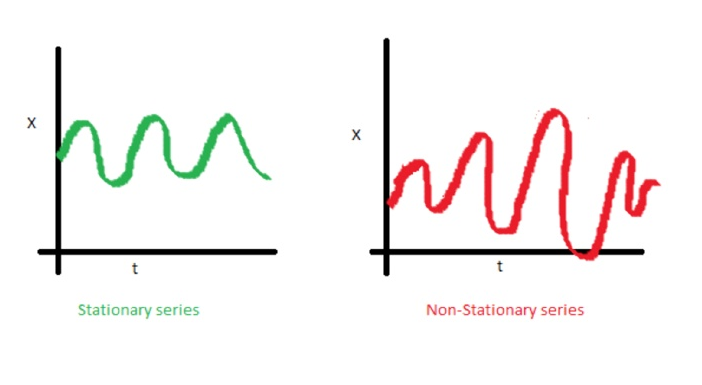
Contoh proses stasioner vs non-stasioner

Garis tren



Dispersi





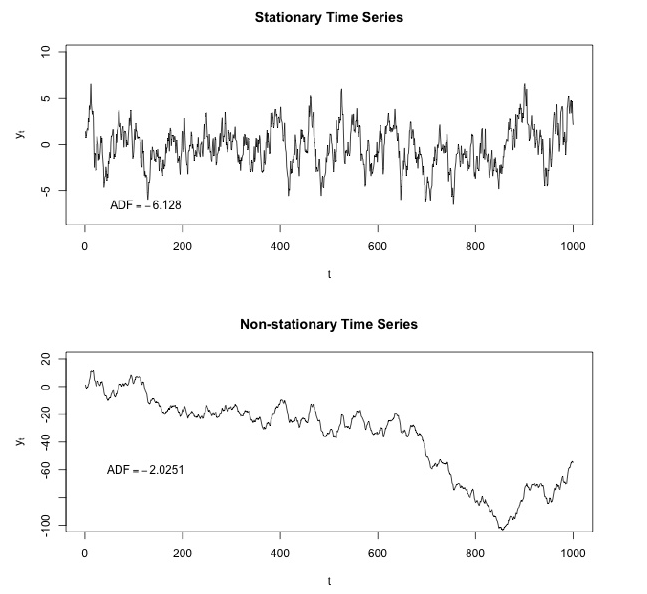
White noise adalah proses statis stokastik yang dapat digambarkan menggunakan dua parameter: rata-rata dan dispersi (varians). Dalam waktu diskrit, white noise adalah sinyal diskrit yang sampelnya dianggap sebagai urutan variabel acak seri tidak berkorelasi dengan nol rata-rata dan varian terbatas.

Jika kita membuat proyeksi ke sumbu y kita dapat melihat distribusi normal. White noise adalah proses gaussian dalam waktu.



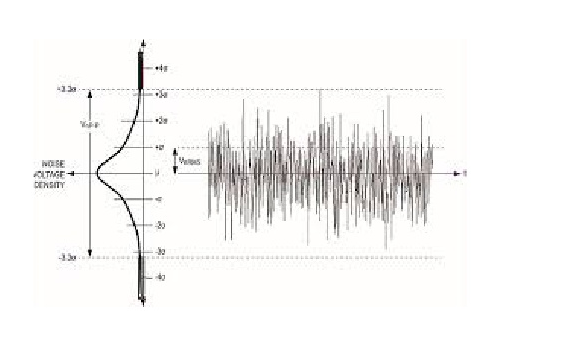
Dalam teori probabilitas, distribusi normal (atau Gaussian) adalah distribusi probabilitas kontinu yang sangat umum. Distribusi normal penting dalam statistik dan sering digunakan dalam ilmu alam dan sosial untuk mewakili variabel acak bernilai nyata yang distribusinya tidak diketahui. Distribusi normal berguna karena teorema limit pusat. Dalam bentuknya yang paling umum, dalam beberapa kondisi (yang termasuk varian terbatas), ia menyatakan bahwa rata-rata sampel pengamatan variabel acak yang diambil secara independen dari distribusi independen bertemu dalam distribusi ke normal, yaitu menjadi terdistribusi normal ketika jumlah pengamatan cukup besar. Kuantitas fisik yang diharapkan merupakan jumlah dari banyak proses independen (seperti kesalahan pengukuran) sering memiliki distribusi yang hampir normal. Selain itu, banyak hasil dan metode (seperti penyebaran ketidakpastian dan pemasangan parameter kuadrat terkecil) dapat diturunkan secara analitis dalam bentuk eksplisit ketika variabel yang relevan terdistribusi secara normal.

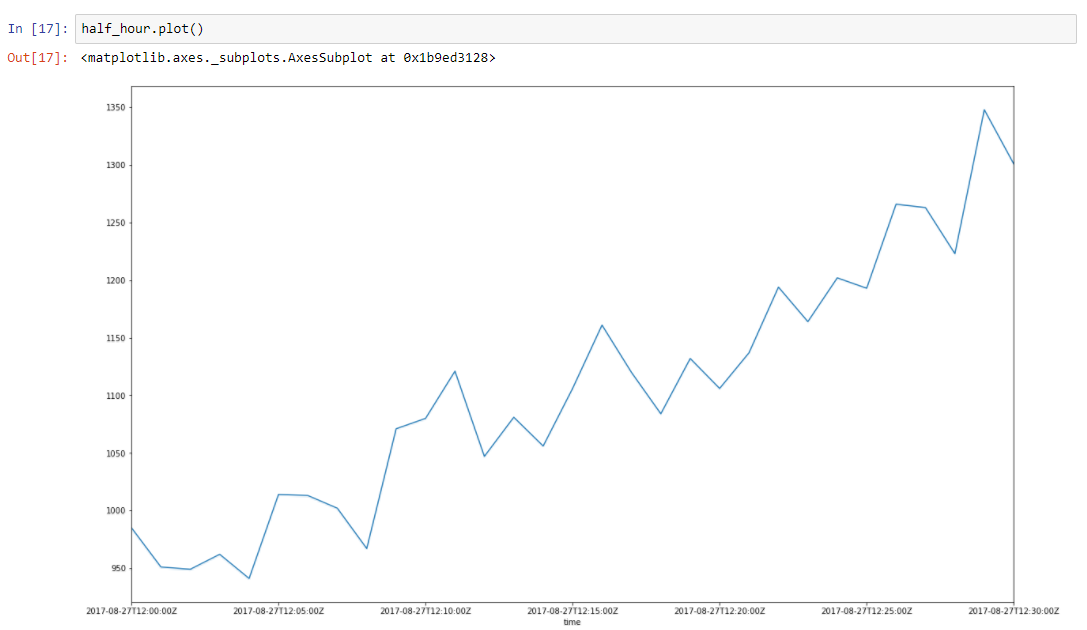
Asumsikan bahwa data kami memiliki tren. Lonjakan di sekitarnya disebabkan oleh banyak faktor acak, yang memengaruhi data kami. Misalnya jumlah permintaan yang dilayani dijelaskan menggunakan pendekatan ini dengan sangat baik. Pengumpulan sampah, kesalahan cache, paging oleh OS, banyak hal mempengaruhi waktu tertentu dari respon yang dilayani. Mari kita ambil setengah jam irisan dari data kami, mulai 2017–08–27 12:00 hingga 12:30. Kita dapat melihat bahwa data ini memiliki tren, dan beberapa osilasi



Mari kita membangun garis regresi untuk menentukan kemiringan garis tren ini.



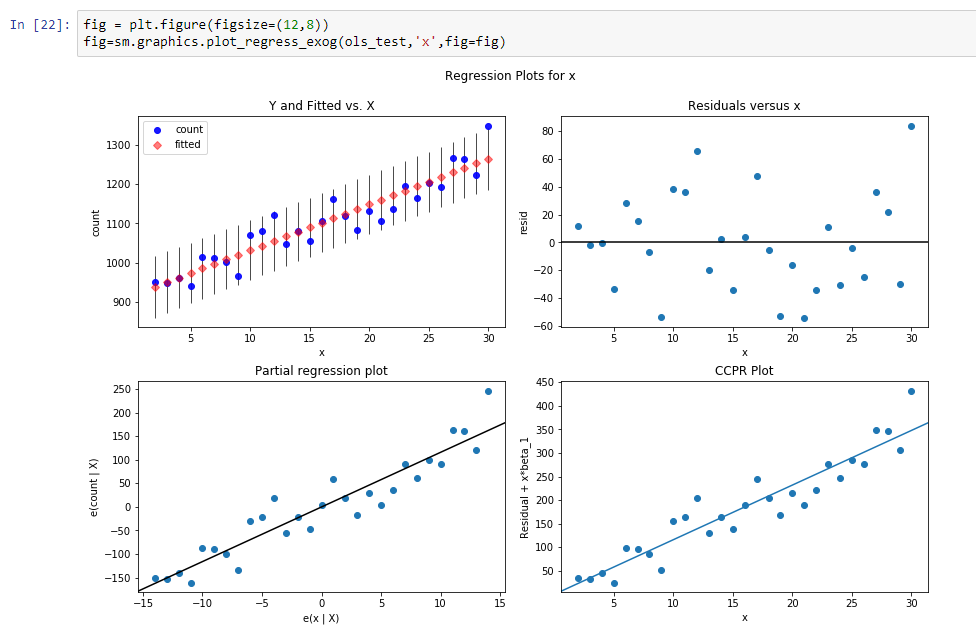
Hasil dari regresi ini adalah:

const 916.269951

dy / dx 11.599507

Hasil berarti, konst tersebut adalah level untuk garis tren ini, dan dy / dx adalah garis kemiringan yang menentukan seberapa cepat level tumbuh sesuai waktu.

Jadi sebenarnya kita mengurangi dimensi data dari 31 parameter menjadi 2 parameter. Jika kita mengurangi dari data awal kita nilai fungsi regresi kita akan melihat proses, yang tampak seperti proses stokastik stasioner.

Jadi setelah pengurangan kita dapat melihat bahwa tren menghilang dan kita dapat mengasumsikan bahwa proses stokastik dalam kisaran ini. Tapi bagaimana kita bisa yakin.



Mari kita membuat Dickey - Tes yang lebih lengkap .

Dickey - Fuller menguji hipotesis nol bahwa deret waktu berakar dan stasioner juga atau menolak hipotesis ini. Jika kita membuat tes Dickey-Fuller pada potongan awal kita, kita akan mendapatkannya



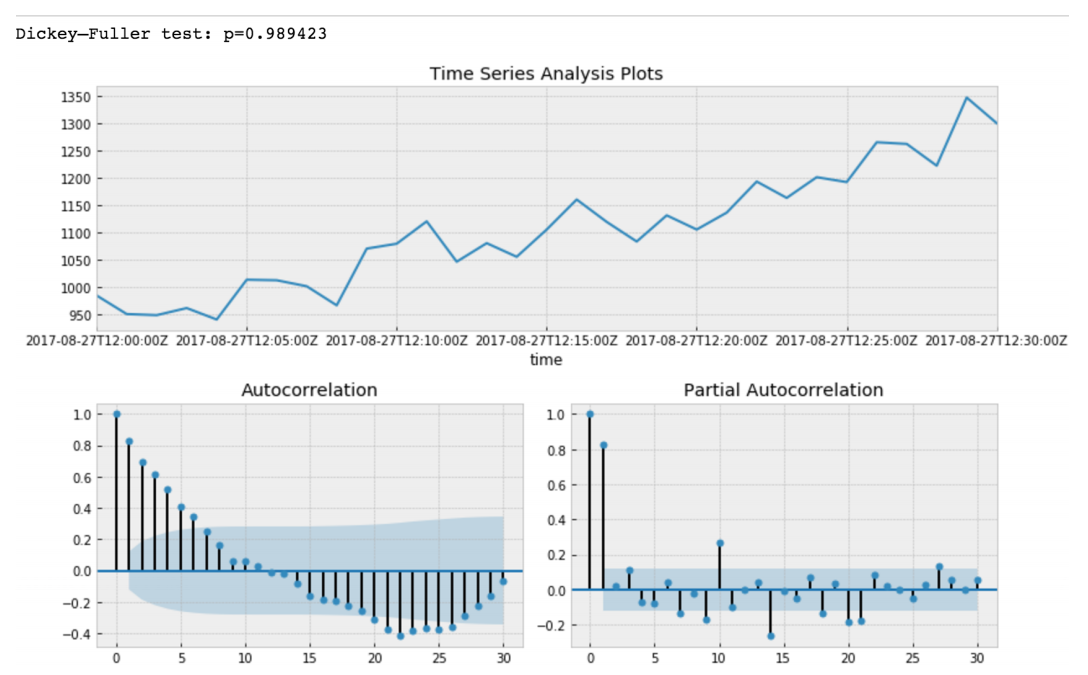
Nilai Tes Dickey-Fuller menolak hipotesis nol dengan keyakinan kuat. Jadi irisan seri waktu kami adalah non-stasioner. Dan kita dapat melihat bahwa Fungsi Autokorelasi menunjukkan autokorelasi tersembunyi.

Setelah pengurangan model regresi kami dari data awal.



Di sini kita dapat melihat bahwa nilai Uji Dickey-Fuller benar-benar kecil dan tidak menolak hipotesis nol tentang tidak stasioneritas pada irisan seri waktu kami. Juga fungsi autokorelasi terlihat baik.

Dengan demikian kami telah melakukan beberapa transformasi data kami dan kami dapat memutar data kami sesuai dengan kemiringan garis tren kami.

Regresi data tersegmentasi

Regresi tersegmentasi , juga dikenal sebagai regresi satu demi satu atau "regresi stick-stick", adalah metode dalam analisis regresi di mana variabel independen dipartisi ke dalam interval dan segmen garis yang terpisah sesuai untuk setiap interval. Analisis regresi tersegmentasi juga dapat dilakukan pada data multivariat dengan mempartisi berbagai variabel independen. Regresi tersegmentasi berguna ketika variabel independen, dikelompokkan ke dalam kelompok yang berbeda, menunjukkan hubungan yang berbeda antara variabel di wilayah ini. Batas antara segmen adalah breakpoints.

Sebenarnya kemiringan kami adalah turunan tersendiri dari deret waktu non stasioner kami karena interval titik metrik kami yang konstan, kami tidak dapat memperhitungkannya dx. Oleh karena itu kami dapat memperkirakan data kami sebagai fungsi piecewise yang dihitung dengan menggunakan turunan diskrit dari tren regresi deret waktu.



Di atas adalah potongan data dari 26–08-2017 00.00 hingga 08.00

Sepertinya ada autokorelasi linier untuk setiap irisan dan jika kami menemukan garis regresi untuk setiap irisan, kami dapat membuat model irisan waktu kami menggunakan asumsi yang kami buat.

Sebagai hasilnya, kita akan memiliki data yang digambarkan menggunakan jumlah parameter minimum yang menguntungkan karena generalisasi yang lebih baik. Vapnik - Dimensi Chervonenkis harus sekecil mungkin untuk generalisasi yang baik.

Dalam teori Vapnik - Chervonenkis, dimensi VC (untuk dimensi Vapnik - Chervonenkis) adalah ukuran kapasitas (kompleksitas, daya ekspresif, kekayaan, atau fleksibilitas) dari ruang fungsi yang dapat dipelajari oleh algoritma klasifikasi statistik. Ini didefinisikan sebagai kardinalitas set poin terbesar yang dapat dihancurkan algoritma. Ini awalnya didefinisikan oleh Vladimir Vapnik dan Alexey Chervonenkis.

Secara formal, kapasitas model klasifikasi terkait dengan seberapa rumitnya itu. Misalnya, perhatikan ambang batas polinomial tingkat tinggi: jika polinomial mengevaluasi di atas nol, titik itu diklasifikasikan sebagai positif, atau negatif. Polinomial tingkat tinggi bisa berubah-ubah, sehingga bisa cocok dengan serangkaian poin pelatihan yang diberikan dengan baik. Tetapi orang dapat berharap bahwa classifier akan membuat kesalahan pada poin lain, karena terlalu goyah. Polinomial semacam itu memiliki kapasitas tinggi. Alternatif yang jauh lebih sederhana adalah dengan threshold fungsi linear. Fungsi ini mungkin tidak sesuai dengan pelatihan yang ditetapkan, karena memiliki kapasitas rendah.

Jadi sebagai hasilnya, kami telah memperkirakan irisan jam kami menggunakan regresi tersegmentasi.



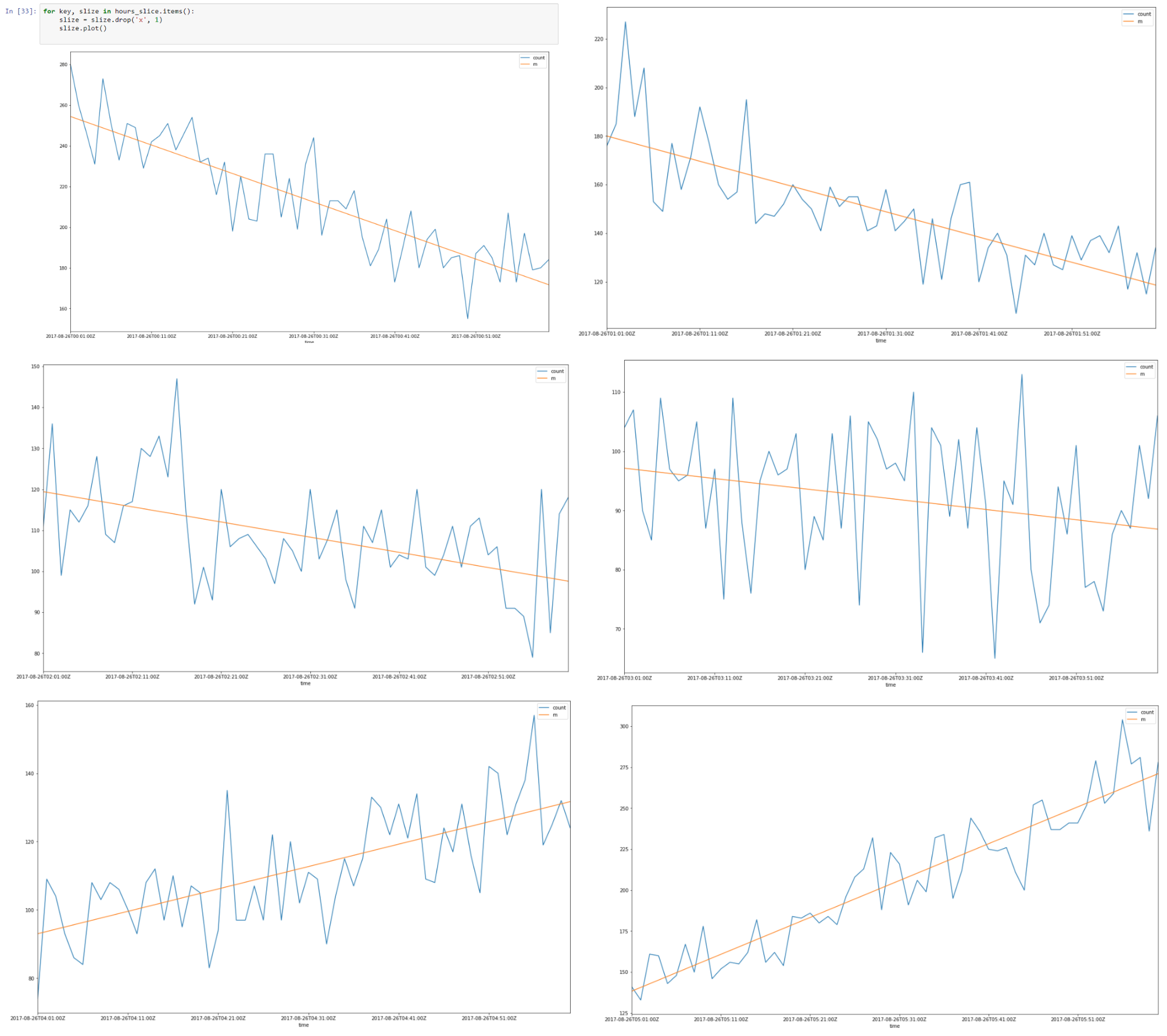
Menyatukan semua irisan 8 jam



Dan menjadikannya stochastic stasioner dengan mengurangkan model regresi.



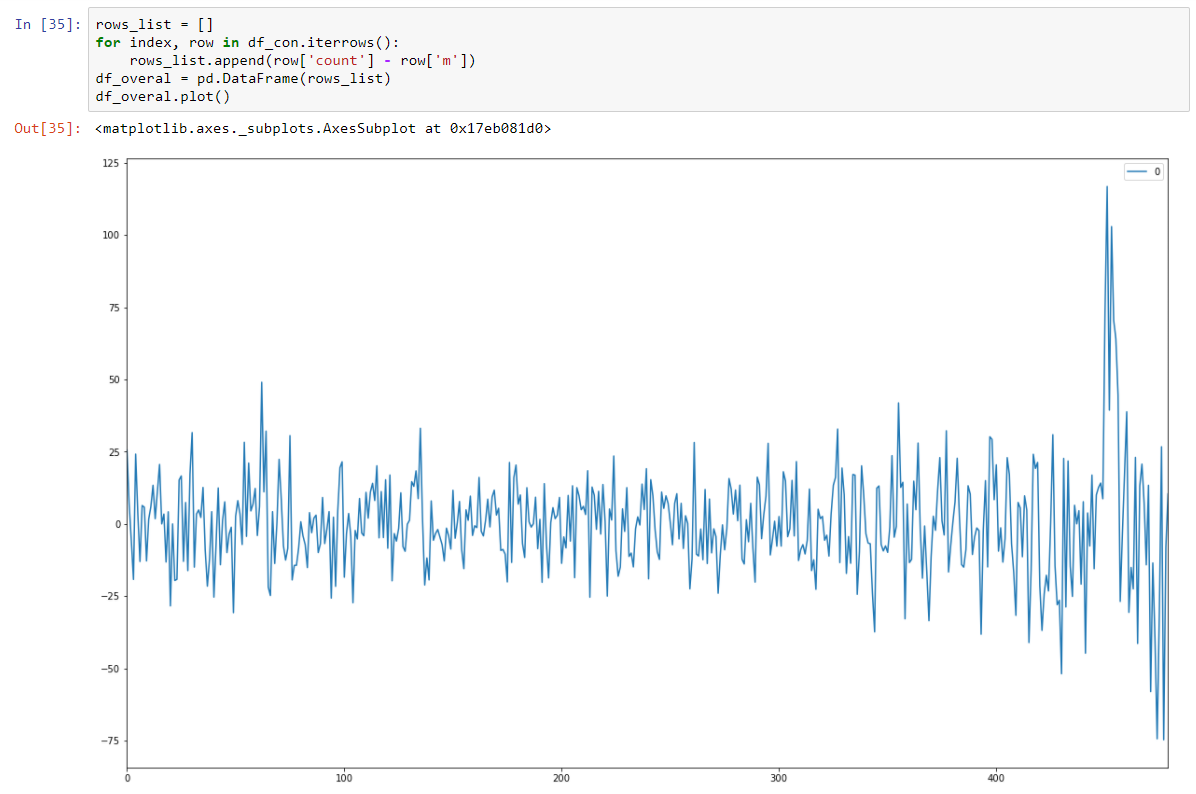
Dan tes Dickey-Fuller kami pada alat tulis ditampilkan dengan keyakinan kuat bahwa kami mengubah data kami menjadi seri alat tulis.



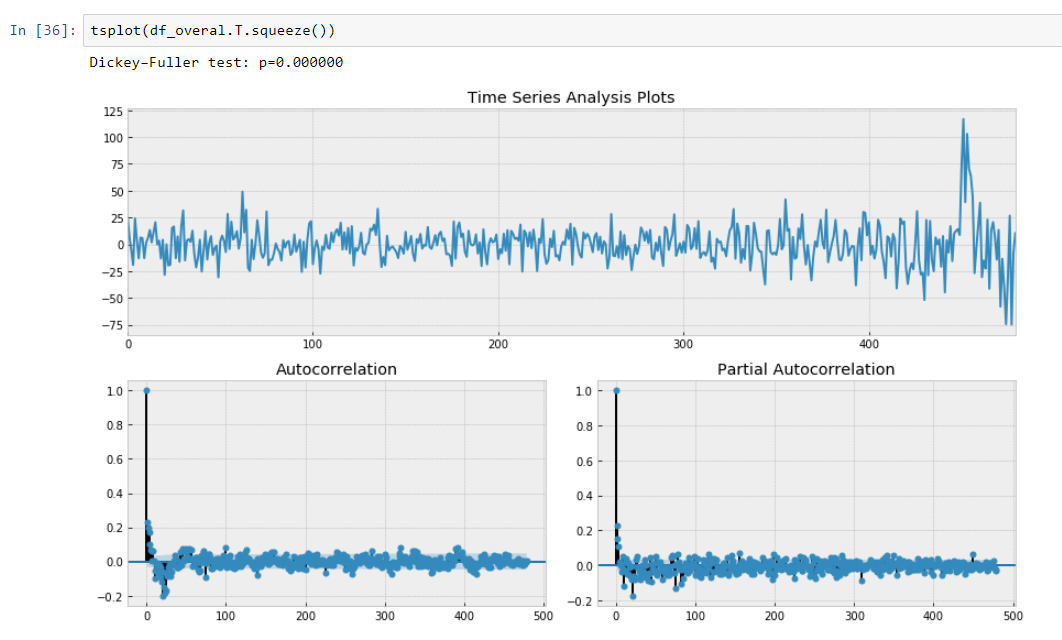
Jadi kami memiliki model prediksi yang menggambarkan data deret waktu kami. Kami telah mengurangi dimensi data kami 15/30 kali lebih kecil!

Sebenarnya kita harus mengembalikan mean prediksi model kita dan mengubahnya kembali menggunakan level dan slope untuk slice tertentu. Ini akan meminimalkan jumlah kesalahan kuadrat untuk prediksi model kami.

Tetapi kita harus menyimpan varians juga karena peningkatan varians dapat menyebabkan adanya faktor-faktor baru yang tidak diketahui dan seperti yang kita ketahui dari pengetahuan domain, memang demikian adanya.

Jadi perubahan varian yang cepat harus diperingatkan juga.

Kami ingin menggunakan model ARIMA juga, tetapi pendekatan yang lebih umum lebih baik, dan kami berencana untuk membandingkan model ini, dan ARIMA standar untuk hasil yang lebih baik. Mari kita lihat seri waktu kami (Hijau adalah semburan varian pada outlier)