🙋🏿 👚 🔥 Mengembangkan hexapod dari awal (bagian 3)

Halo semuanya! Perkembangan hexapod semakin maju dan akhirnya bagian matematika dasar telah diuji dan siap untuk didokumentasikan. Agar proyek bertahan sampai akhir dan tidak mengumpulkan debu di rak, Anda perlu melihat perubahan positifnya, bahkan jika itu tidak signifikan. Pada artikel ini, saya akan berbicara tentang algoritma untuk menyelesaikan masalah kinematika terbalik dan menunjukkannya dalam tindakan. Saya harap ini akan menarik.

Tahapan pengembangan:
Bagian 1 - Desain
Bagian 2 - perakitan
Bagian 3 - Kinematika
Bagian 4 - lintasan dan urutan matematika
Bagian 5 - Elektronik
Bagian 6 - transisi ke pencetakan 3D
Bagian 7 - perumahan baru, perangkat lunak aplikasi, dan protokol komunikasi

Sistem koordinat

Untuk memulainya, perlu untuk menentukan sistem koordinat robot - ada sebanyak tiga dari mereka:

Pada kenyataannya, mereka tidak berbeda satu sama lain, tetapi terletak di tempat yang berbeda dari kasus ini dan dapat diputar relatif satu sama lain di beberapa sudut. Jika dilihat dari atas, lokasi sumbu akan sebagai berikut (parameter coxa_zero_rotate akan dijelaskan sedikit kemudian):

Seperti yang mungkin sudah Anda perhatikan, sistem koordinat di sisi kiri dan kanan terletak secara simetris relatif terhadap pusat tubuh. Bagi saya tampaknya akan lebih mudah.

Koordinat setiap titik diatur relatif terhadap ekstremitas yang dimaksudkan titik ini. Pendekatan ini memungkinkan Anda untuk memindahkan anggota badan ke mana saja tanpa mengganggu konfigurasi.

Dan karena itu mereka berada relatif terhadap anggota tubuh:

Koordinat titik target relatif terhadap SISTEM KOORDINAT UTAMA. Awalnya, saya ingin mengatur koordinat relatif ke pusat kasing, tetapi ini ternyata tidak terlalu nyaman dan memerlukan penyimpanan sejumlah parameter tambahan.

Selanjutnya, notasi X *, X **, dll. akan diganti oleh X ′, X ′ ′.

Memecahkan masalah kinematika terbalik

Mari kita mulai dengan momen paling sulit dan menarik bagi saya - kinematika. Saya menemukan algoritma sendiri, kadang-kadang melirik sifat-sifat segitiga dan fungsi trigonometri. Dengan mekanik, itu sulit bagi saya, dan dengan trigonometri itu bahkan lebih buruk, jadi mungkin di suatu tempat saya tidak dapat memperhitungkan sesuatu, tetapi algoritma ini berfungsi (video pada akhirnya).

1. Pernyataan masalah

Misalkan kita memerlukan tungkai kanan depan untuk mencapai titik A dengan koordinat (150; -20; 100). Diketahui juga bahwa ekstremitas diputar relatif terhadap tubuh sebesar 45 derajat (parameter coxa_zero_rotate):

Anggota gerak itu sendiri memiliki parameter berikut:

Saya pikir Anda tidak perlu menjelaskan apa arti parameter ini, nama-nama berbicara sendiri. Anda hanya dapat menambahkan bahwa semua parameter ini ditentukan oleh konfigurasi case, permanen dan disimpan dalam memori FLASH dengan kemampuan untuk mengedit dari luar (untuk fleksibilitas).

Itu sebabnya kamu membutuhkannya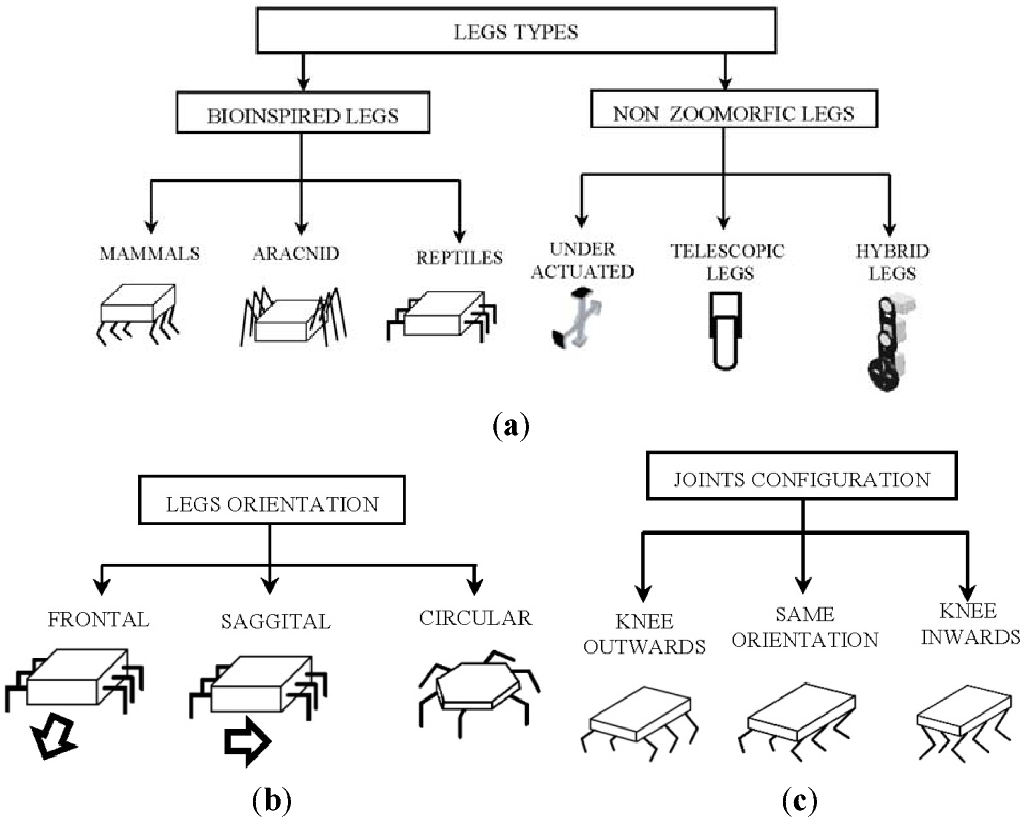

Gambar menunjukkan berbagai variasi lambung dan lokasi kaki-kaki hexapod. Sekarang cocok dengan konfigurasi ARACNID. Misalkan terpikir oleh saya untuk mengubah case menjadi REPTILES, dan untuk ini akan cukup sederhana untuk mengubah nilai-nilai parameter tanpa pengukuran dalam program itu sendiri, bahkan titik-titik target tidak harus diubah (kecuali tentu saja dengan benar mendekati ini).

Semua parameter di atas sudah cukup untuk menyelesaikan masalah.

2. Solusi untuk masalah tersebut

2.1 Menemukan sudut rotasi COXA

Tahap ini adalah yang paling sederhana. Pertama, Anda perlu menghitung ulang koordinat titik A relatif terhadap SISTEM KOORDINAT LIMB. Jelas, Anda perlu memutar sudut coxa_zero_rotate, Anda dapat melakukan ini menggunakan rumus berikut:

$$ menampilkan $$ x ′ = x ⋅ cos (α) + z ⋅ sin (α) = 150 ⋅ cos (45) + 100 ⋅ sin (45) = 176.78 $$ menampilkan $$

$y ′ = y = -20$

$$ menampilkan $$ z ′ = -x ⋅ sin (α) + z ⋅ cos (α) = -150 ⋅ sin (45) + 100 ⋅ cos (45) = -35,36 $$ menampilkan $$

Dengan demikian, kami mendapat koordinat titik target A (176,78; -20; -35,36) relatif terhadap LIMB COORDINATE SYSTEM.

Sekarang Anda dapat menemukan sudut COXA menggunakan fungsi atan2:

$COXA = atan2 (z ′, x ′) = atan2 (-35.36, 176.78) = -11.30 °$

Jadi, kita mendapatkan sudut di mana Anda perlu memutar servo COXA sehingga titik A berada di bidang X′Y ′. Sekarang mari kita periksa perhitungan kita dalam KOMPAS 3D:

Baiklah

2.2 Menemukan sudut rotasi FEMUR dan TIBIA
Untuk menemukan sudut-sudut ini, perlu untuk pergi ke pesawat X′Y ′. Untuk pergi ke pesawat, Anda perlu memutar titik dengan sudut COXA, yang sudah kita hitung sebelumnya.

$$ menampilkan $$ x ′ = x ′ ⋅ cos (α) + y ′ ⋅ sin (α) = 176,78 ⋅ cos (-11) + -20 ⋅ sin (-11) = 180,28 $$ menampilkan $$

$y ′ = y = -20$

Koordinat y ′ tidak berubah, karena kami berputar di sepanjang sumbu Y ′.

Selanjutnya, Anda perlu menghapus panjang COXA dari perhitungan, mis. kami melewati ke pesawat X′′Y ′ ′, untuk ini kami melakukan pergeseran koordinat x ′ dari titik dengan panjang COXA:

$x ′ ′ = x ′ - coxaLength = 180.28 - 40 = 140.28$

$y ′ ′ = y ′$

Setelah semua manipulasi ini, solusi lebih lanjut dari masalah dikurangi untuk menemukan sudut a dan b dari segitiga:

Sebelum menemukan sudut, Anda harus menemukan sisi ketiga C dari segitiga ini. Jarak ini tidak lain adalah panjang vektor dan dihitung dengan rumus:

$$ tampilkan $$ C = \ sqrt {x ′ ′ ^ 2 + y ′ ′ ^ 2} = \ sqrt {140.28 ^ 2 + (-20) ^ 2} = 141.70 $$ tampilkan $$

Sekarang Anda perlu memeriksa apakah anggota badan dapat mencapai titik ini. Jika C lebih besar dari jumlah panjang FEMUR dan TIBIA, maka titik tersebut tidak dapat dijangkau. Dalam kasus kami, 141,70 <141 + 85 - intinya dapat dicapai.

Sekarang kita tahu semua sisi segitiga dan kita dapat menemukan sudut a dan b yang kita butuhkan menggunakan teorema kosinus:

$a = acos ({A ^ 2 + C ^ 2 - B ^ 2 \ lebih dari 2AC}) = 72,05 °$

$b = acos ({B ^ 2 + A ^ 2 - C ^ 2 \ lebih dari 2BA}) = 72,95 °$

Sudut yang diperoleh tidak berlaku untuk mengumpankan mereka ke servos, karena posisi awal dan sudut kemiringan garis lurus C ke sumbu X tidak diperhitungkan di sini. Jika kita tahu sudut awal FEMUR dan TIBIA (135 ° dan 45 °), maka sudut kemiringan C ke sumbu X tidak dikenal. Anda dapat menemukannya menggunakan fungsi atan2 (y ′ ′, x ′ ′):

$$ tampilan $$ φ = atan2 (y ′ ′, x ′ ′) = atan2 (-20, 140,28) = -8,11 ° $$ display $$

Akhirnya, Anda dapat menghitung sudut rotasi servos FEMUR dan TIBIA:

$FEMUR = femurZeroRotate - a - φ = 135 - 72.05 + 8.11 = 71.06 °$

$FEMUR = b - tibiaZeroRotate = 45 - 72.95 = 27.95 °$

Mari kita periksa perhitungan kita:

Sepertinya kebenaran.

Ringkasan

Sudut terhitung COXA, FEMUR dan TIBIA cocok untuk memberi makan servos mereka. Anda mungkin memperhatikan bahwa sudut COXA negatif dan, oleh karena itu, muncul pertanyaan: "Bagaimana cara memutar drive dengan -11,3 derajat?". Kuncinya adalah bahwa saya menggunakan posisi netral servo COXA sebagai nol logis, ini memungkinkan drive untuk memutar sudut positif dan negatif. Ini tentu saja jelas, tetapi saya pikir tidak akan salah menyebutkan hal ini. Saya akan membicarakan hal ini lebih terinci dalam artikel-artikel berikut ketika saya berbicara tentang implementasi semua hal di atas.

Kode sumber

Cukup kata-kata, biarkan saya melihat kode

#define RAD_TO_DEG(rad) ((rad) * 180.0 / M_PI) #define DEG_TO_RAD(deg) ((deg) * M_PI / 180.0) typedef enum { LINK_COXA, LINK_FEMUR, LINK_TIBIA } link_id_t; typedef struct { // Current link state float angle; // Link configuration uint32_t length; int32_t zero_rotate; int32_t min_angle; int32_t max_angle; } link_info_t; typedef struct { point_3d_t position; path_3d_t movement_path; link_info_t links[3]; } limb_info_t; // *************************************************************************** /// @brief Calculate angles /// @param info: limb info @ref limb_info_t /// @return true - calculation success, false - no // *************************************************************************** static bool kinematic_calculate_angles(limb_info_t* info) { int32_t coxa_zero_rotate_deg = info->links[LINK_COXA].zero_rotate; int32_t femur_zero_rotate_deg = info->links[LINK_FEMUR].zero_rotate; int32_t tibia_zero_rotate_deg = info->links[LINK_TIBIA].zero_rotate; uint32_t coxa_length = info->links[LINK_COXA].length; uint32_t femur_length = info->links[LINK_FEMUR].length; uint32_t tibia_length = info->links[LINK_TIBIA].length; float x = info->position.x; float y = info->position.y; float z = info->position.z; // Move to (X*, Y*, Z*) coordinate system - rotate float coxa_zero_rotate_rad = DEG_TO_RAD(coxa_zero_rotate_deg); float x1 = x * cos(coxa_zero_rotate_rad) + z * sin(coxa_zero_rotate_rad); float y1 = y; float z1 = -x * sin(coxa_zero_rotate_rad) + z * cos(coxa_zero_rotate_rad); // // Calculate COXA angle // float coxa_angle_rad = atan2(z1, x1); info->links[LINK_COXA].angle = RAD_TO_DEG(coxa_angle_rad); // // Prepare for calculation FEMUR and TIBIA angles // // Move to (X*, Y*) coordinate system (rotate on axis Y) x1 = x1 * cos(coxa_angle_rad) + z1 * sin(coxa_angle_rad); // Move to (X**, Y**) coordinate system (remove coxa from calculations) x1 = x1 - coxa_length; // Calculate angle between axis X and destination point float fi = atan2(y1, x1); // Calculate distance to destination point float d = sqrt(x1 * x1 + y1 * y1); if (d > femur_length + tibia_length) { return false; // Point not attainable } // // Calculate triangle angles // float a = tibia_length; float b = femur_length; float c = d; float alpha = acos( (b * b + c * c - a * a) / (2 * b * c) ); float gamma = acos( (a * a + b * b - c * c) / (2 * a * b) ); // // Calculate FEMUR and TIBIA angle // info->links[LINK_FEMUR].angle = femur_zero_rotate_deg - RAD_TO_DEG(alpha) - RAD_TO_DEG(fi); info->links[LINK_TIBIA].angle = RAD_TO_DEG(gamma) - tibia_zero_rotate_deg; // // Check angles // if (info->links[LINK_COXA].angle < info->links[LINK_COXA].min_angle || info->links[LINK_COXA].angle > info->links[LINK_COXA].max_angle) { return false; } if (info->links[LINK_FEMUR].angle < info->links[LINK_FEMUR].min_angle || info->links[LINK_FEMUR].angle > info->links[LINK_FEMUR].max_angle) { return false; } if (info->links[LINK_TIBIA].angle < info->links[LINK_TIBIA].min_angle || info->links[LINK_TIBIA].angle > info->links[LINK_TIBIA].max_angle) { return false; } return true; }

Algoritma dalam aksi

Kemudian, secara kebetulan, urutan muncul yang agak mengingatkan pada tarian

PS

Saya akan senang jika ada yang bisa menyederhanakan algoritma ini. Saya membuatnya sehingga saya bisa memahaminya setelah, katakanlah, setengah tahun.

Mengembangkan hexapod dari awal (bagian 3) - kinematika