Pernyataan masalah

Saya berselancar di Internet tempo hari dan ada sesuatu yang agak aneh yang menarik perhatian saya: motor Mendocino . Ini adalah rotor bantalan gesekan sangat rendah: yang asli memiliki silinder kaca tergantung pada dua jarum, tetapi yang modern menggunakan suspensi magnetik. Ini adalah mesin tanpa sikat: rotor memiliki baterai surya yang terpasang padanya, yang menghasilkan arus untuk gulungan yang melilit rotor. Rotor berputar di medan magnet tetap, baterai surya terkena sumber cahaya satu demi satu. Ini adalah solusi yang agak elegan yang sangat mungkin untuk dibuat ulang di rumah.

Inilah video yang menjelaskan cara kerjanya (dalam bahasa Rusia):


Tetapi video ini memiliki rasa ingin tahu lain yang bahkan lebih kuat dari mesin itu sendiri. Dalam deskripsi video, Dmitry Korzhevsky menulis: "Anda TIDAK BISA mengganti dukungan sisi dengan magnet! Jangan tanya aku lagi tentang ini! ”

DIsclaimer: Saya bukan ahli fisika dan mungkin sangat keliru dalam beberapa hal, jadi koreksi dipersilahkan.



Mari kita bahas sekali lagi bagaimana sistem suspensi magnetik rotor bekerja. Jika kita mengambil dua magnet, maka isolin potensial terlihat seperti ini, tergantung pada jarak antara magnet:



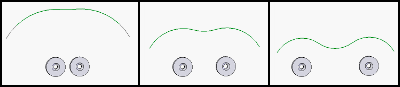
Jadi, kami menempatkan dua magnet tetap pada stator. Magnet yang diletakkan pada poros rotor tidak akan mau bergerak ke samping, karena isolin potensial memiliki titik minimum lokal tertentu. Sebagai gantinya, ia ingin meletus sepanjang sumbu rotor. Kami membuat dua dari sistem ini dan pada akhirnya, sumbu rotor stabil secara radial, tetapi tidak stabil secara lateral. Kami memperbaikinya dengan mengarahkan rotor ke dinding kaca dan voila - kami memiliki bantalan gesekan rendah.

Tapi dinding kacanya sedikit ... tidak menyenangkan secara estetika, bukan? Hanya logis kami ingin menangguhkan rotor di udara sepenuhnya, tanpa kruk mekanik seperti ini. Dan ternyata, Dmitry juga dibombardir dengan pertanyaan yang sama, oleh karena itu ia harus mencatat tepat dalam deskripsi bahwa itu tidak mungkin. Dan saya yakin Dmitry bukan satu-satunya yang bosan dengan ini.

Mari kita lihat ini, saya kutip:

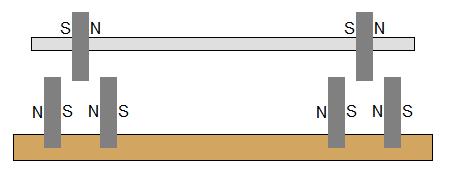
Apa yang akan terjadi jika magnet dasar ditempatkan dan diorientasikan seperti pada gambar ini? Apakah ini akan memberikan stabilitas di bidang aksial, dan menghilangkan persyaratan cermin?

Atau di sini , saya kutip:

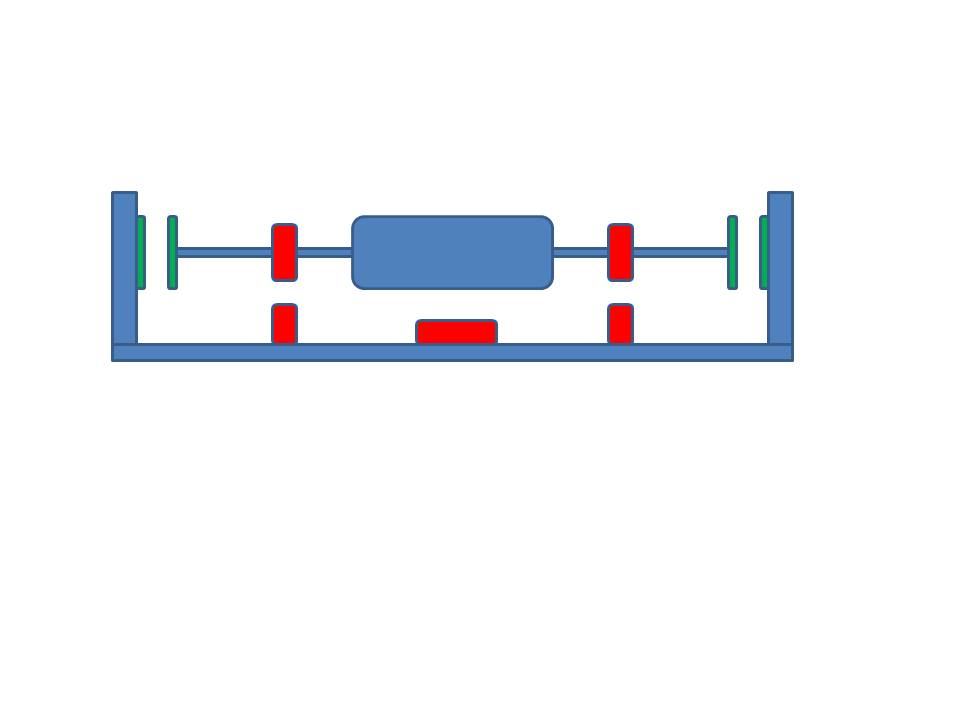
Pada Mendocino Motor mengapa satu sisi mengambang bebas sementara yang lain memiliki ujung ke dinding? Saya tahu pertanyaannya mungkin terdengar sepele, tetapi saya telah memikirkan mengapa tidak menggunakan magnet yang sama yang digunakan untuk melayang sebagai kekuatan pengimbang di kedua sisi poros? Saya memasang jpg yang sangat kasar dari apa yang saya maksud. magnet hijau di ujung poros adalah apa yang saya maksudkan. Adakah teori atau hukum yang mencegah hal ini?

Kita dapat melihat bahwa banyak orang di seluruh dunia ingin menyingkirkan bagian mekanis yang tidak pantas ini. Saya tidak menaruh banyak perhatian di masa sekolah saya, jadi sama sekali tidak jelas bagi saya mengapa sistem suspensi magnetik yang sepenuhnya stabil tidak mungkin dilakukan. Suatu hari saat makan siang saya menanyakan pertanyaan itu kepada penyelia saya, seorang ilmuwan terkenal di dunia (dalam matematika terapan, bukan fisika): "Mengapa tidak mungkin?". Dan Anda tahu, dia juga tidak tahu!

Forum yang diposting di atas juga tidak memberikan jawaban yang tepat untuk pertanyaan itu. Best-case, seseorang merujuk pada sesuatu yang disebut teorema Earnshaw , yang tidak cocok untuk dipahami pada pandangan pertama. Ini menyatakan bahwa: kumpulan muatan titik tidak dapat dipertahankan dalam konfigurasi kesetimbangan stasioner yang stabil semata-mata oleh interaksi elektrostatik dari muatan tersebut. Apakah kamu mengerti? Tentu saja tidak. Katakanlah saya dapat menerima kenyataan bahwa kita sedang membicarakan tuduhan dan bukan magnet. Lalu apa?

Ilustrasi pertama

Ketika saya tidak bisa membungkus kepala saya dengan sesuatu, saya cenderung menggambarnya. Mari kita ilustrasikan ini dalam 2D, untuk kesederhanaan. Bayangkan empat biaya tetap, ditempatkan dalam pola persegi, ditambah biaya gratis di tengah. Seperti ini:



Bukankah biaya gratis dalam keseimbangan? Ke mana pun ia bergerak, ia akan semakin mendekati salah satu muatan tetap, yang meningkatkan daya dorong! Mari kita coba menggambar peta energi potensial biaya gratis. Saya melewatkan banyak kelas fisika di sekolah, jadi repositori pengetahuan saya ada Wikipedia. Jadi, jika Anda hanya memiliki satu muatan tetap, maka itu menciptakan potensi elektrostatik di bidang di sekitarnya:

Persamaan untuk potensial elektrostatik (atau potensial Coulomb) dari muatan titik dalam ruang hampa:

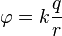
Dalam semua eksperimen pemikiran saya, semua koefisien adalah 0 atau 1. Jadi muatan q adalah 1, dan k yang tidak diketahui juga 1. Itu berarti bahwa satu muatan tetap menciptakan energi potensial yang diukur sebagai 1 / r, di mana r adalah jarak ke biaya.

Dalam kasus kami, energi potensial dari muatan gratis dalam bidang muatan tetap juga sama dengan 1 / r. (Agar adil, energinya sama dengan k * q1 * q2 / r, tapi kami memilih koefisien untuk mempermudah perhitungan). Untuk beberapa tagihan, kami cukup menambahkan semua potensi.

Mari kita menggambar peta energi potensial dari biaya gratis kami. Saya menggunakan bijak untuk ini:

var('x,y') def unit_potential(a,b,x,y): return 1/(sqrt((xa)^2 + (yb)^2)) def system_potential(x,y): return unit_potential(1,1,x,y)+unit_potential(-1,1,x,y)+unit_potential(1,-1,x,y)+unit_potential(-1,-1,x,y) contour_plot(system_potential(x,y), (x, -2, 2), (y, -2, 2), cmap='hsv', contours=30, region=5-system_potential(x,y), figsize=12, colorbar=True) 

Ini peta kita. Titik putih (tertusuk) adalah di mana energi potensial menjadi tak terbatas:



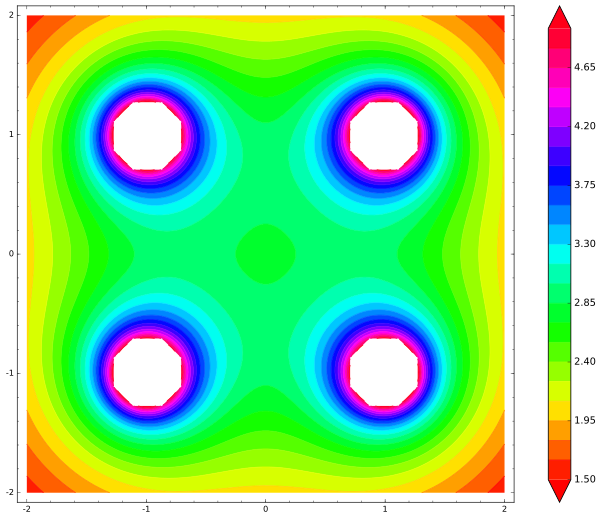
Kami jelas melihat minimum energi lokal di pusat. Di mana pun muatan pusat ingin bergerak, energi akan meningkat, sehingga gangguan kecil akan memaksanya kembali ke pusat - titik keseimbangan stabil. Apakah Earnshaw salah, kalau begitu? Tidak, dia tidak, saya hanya menggambar ilustrasinya dengan tidak benar. Dan itu adalah kesalahan umum di antara orang-orang yang mengajukan pertanyaan itu. Berhentilah selama beberapa menit sekarang dan tebak: apa yang saya lewatkan?

Bahkan, dalam kasus ini, kesalahannya adalah bahwa dalam ruang dua dimensi, muatan tetap menciptakan energi potensial yang diukur sebagai -ln r, di mana r adalah jarak ke muatan, dan bukan 1 / r. Ambil saja kata-kata saya untuk saat ini dan biarkan saya memperbaiki persamaannya tanpa menjelaskan banyak hal. Kode yang benar terlihat seperti ini:

 var('x,y') def unit_potential(a,b,x,y): return -ln(sqrt((xa)^2 + (yb)^2)) def system_potential(x,y): return unit_potential(1,1,x,y)+unit_potential(-1,1,x,y)+unit_potential(1,-1,x,y)+unit_potential(-1,-1,x,y) contour_plot(system_potential(x,y), (x, -2, 2), (y, -2, 2), cmap='hsv', contours=30, region=5-system_potential(x,y), figsize=12, colorbar=True) 

Dan ini adalah peta yang dihasilkannya:



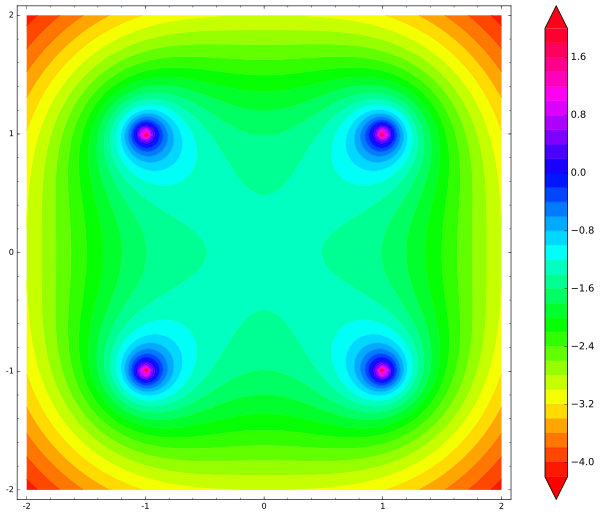
Perhatikan bahwa tidak ada minimum lokal di mana pun. Pusat adalah titik pelana, atau titik keseimbangan yang tidak stabil . Begitu muatan gratis bergerak bahkan satu mikron menjauh dari pusat, itu pasti akan terbang keluar dari sistem, mempercepat di sepanjang jalan,

Tunggu sebentar, apa yang baru saja Anda lakukan untuk persamaan?

Awalnya, ketika saya menyadari bahwa perhitungan saya benar-benar bertentangan dengan teorema Earnshaw, saya menyadari bahwa saya membuat kesalahan di suatu tempat. Paling mudah untuk melacak langkah-langkah saya dari awal. Aku menghela nafas panjang dan membaca persamaan Maxwell . Sekali lagi, saya tidak terlalu bagus di sekolah: tidak di kelas (ini sangat bagus), tetapi dalam jumlah pengetahuan yang saya ambil darinya. Misalnya, saya langsung lupa dengan persamaan Maxwell, karena di universitas dan seterusnya saya tidak perlu bekerja dengan mereka.

Ternyata itu cukup sederhana, terutama jika kita berbicara tentang hukum elektrostatik saja! Ada empat persamaan Maxwell, satu untuk masing-masing hukum ini:

• Hukum Gauss, kita akan membutuhkannya nanti. Singkatnya, ini adalah hukum konservasi: energi tidak dapat diciptakan dari ketiadaan, juga tidak dapat dihancurkan.
• Hukum Gauss untuk medan magnet, yang pada dasarnya adalah hal yang sama. Dan kita belum masuk ke medan magnet, karena kita hanya berbicara tentang partikel bermuatan. Lewati hukum itu.
• Hukum Faraday: magnet yang bergerak menciptakan medan listrik. Itu menarik, kita akan melihatnya nanti.
• Hukum Amper: menggerakkan medan listrik menciptakan medan magnet. Tidak berguna untuk tujuan kita.

Jadi, keempat hukum ini mengikat dua vektor E dan B, medan listrik dan magnet. Vektor ini adalah fungsi dengan empat argumen (x, y, z, t) dan masing-masing empat argumen akan disandingkan dengan satu vektor tiga dimensi. Kita tidak begitu tertarik pada medan magnet, jadi mari kita lihat medan listrik, atau E (x, y, z, t). Jangan lupa kita berada di dunia elektrostatik, jadi E konstan sepanjang waktu. Anda dapat membayangkan vektor ini sebagai sungai, di mana pada setiap titik kami mengatakan di mana dan seberapa cepat air mengalir.

Hukum Faraday menyatakan bahwa bidang E waktu-konstan (kita berbicara elektrostatik di sana) tidak memiliki ikal .

Bagaimana potensi elektrostatik terhubung ke medan listrik? Sederhana: jika bidang E-curl-kurang (seperti halnya di sana), maka kita dapat membuat Anda dengan cara itu (kembali ke contoh sungai), ditutupi oleh lapisan air 1 meter (di semua ketinggian! ) dan “melepaskan: itu, kecepatan dan arah aliran air akan menciptakan bidang E. Atau, dalam istilah matematika, dimungkinkan untuk menemukan fungsi skalar u, gradien yang sama dengan bidang E.

Hukum Gauss menyatakan: ambil lingkungan kecil. Jika kami tidak sengaja memasukkan biaya, maka jumlah "air" yang mengalir ke lingkungan sama dengan jumlah yang mengalir keluar. Jika kita ingin terdengar pintar, divergensi bidang E adalah nol.

Ingat: bidang E adalah turunan dari fungsi skalar u. Jika perbedaannya adalah nol, maka itu berarti laplacian dari Anda adalah nol. Laplacian adalah kata yang cerdas untuk "kelengkungan" fungsi. Jika kita berbicara tentang fungsi satu variabel, laplacian hanyalah turunan kedua. Dalam fungsi dua variabel, laplacian adalah jumlah dari dua turunan. Jika sama dengan nol, maka lengkungan di satu arah harus dibatalkan oleh lengkungan di arah lain. Artinya, keripik bisa ada:



Tetapi fungsi zero-laplacian tidak memiliki minimum lokal (atau maksimum), yang berarti keripik diperbolehkan, tetapi bukit tidak:



Bayangkan mencelupkan lingkaran kawat ke air sabun. Film sabun kemudian membentuk permukaan zero-laplacian:



Itu akan disebut "permukaan minimal". Film sabun berusaha sekecil mungkin, jadi masuk akal jika memiliki maksimum lokal tertentu, kita akan memiliki film yang lebih kecil dengan menghaluskannya, jadi tidak ada. Jadi, potensi elektrostatik adalah semacam permukaan minimal yang tidak memiliki maksimum lokal (selama kami tidak menempatkan muatan di sana dengan sengaja).

Fungsi 1 / r memiliki nol laplacian dalam tiga dimensi, tetapi tidak dalam dua! Jika kita ingin menggambar contoh dua dimensi, kita perlu menyelesaikan masalah Dirichlet - untuk 2D, itu -ln r.

Menggunakan rumus kuadrat terbalik dalam ruang 1 atau 2 dimensi berhubungan dengan membatasi pergerakan muatan sepanjang sumbu yang tersisa dengan cara lain. Dalam hal ini, jelas bahwa memungkinkan untuk membuat konfigurasi yang stabil - cukup ambil tabung kardus, letakkan secara vertikal dan letakkan magnetnya. Maka dimungkinkan untuk menempatkan ada satu magnet lagi yang akan seimbang - secara horizontal dibatasi oleh tabung (yaitu dalam ruang satu dimensi), dan pada gaya gravitasi gravitasi vertikal dan tolakan magnet diimbangi. Teorema Earnshaw perlu diterapkan dengan hukum kuadrat terbalik - tetapi dalam 3d, atau dalam ruang dimensi apa pun, tetapi dengan potensi yang sesuai. "Corresponding" berarti yang diperoleh dari persamaan Maxwell.

Teorema Earnshaw dan konsekuensinya

Jadi, kembali ke contoh kita dengan satu partikel bermuatan gratis. Potensi medan elektrostatik tidak memiliki minimum lokal dan, sebagai hasilnya, energi potensial partikel tidak memiliki minimum lokal. Jadi satu partikel tidak dapat mencapai kesetimbangan stabil dalam medan statis. Selamat, kami baru saja membuktikan teorema Earnshaw. Tetapi bagaimana dengan sistem yang lebih rumit? Bagaimana cara menerapkan teorema di sana?

Berikut ini contoh lain yang, menurut bos saya, seharusnya tidak membuktikan teorema Earnshaw. Mari kita perbaiki dua muatan dan membuat benda bergerak yang terdiri dari tongkat yang beratnya tak terukur dengan muatan di kedua ujungnya:



Secara intuitif, jika kita memindahkan tongkat sedikit ke kiri atau ke kanan, maka salah satu ujungnya akan semakin mendekati muatan yang ditetapkan, yang akan mendorongnya menjauh dan mengembalikan tongkat ke posisi semula. Jadi, apa masalahnya? Mari kita menggambar peta potensi elektrostatik dari dua muatan tetap:

 var('x,y') def unit_potential(a,b,x,y): return -ln(sqrt((xa)^2 + (yb)^2)) def system_potential(x,y): return unit_potential(0,1,x,y)+unit_potential(0,-1,x,y) contour_plot(system_potential(x,y), (x, -2, 2), (y, -2, 2), cmap='hsv', contours=30, figsize=12, colorbar=True) 

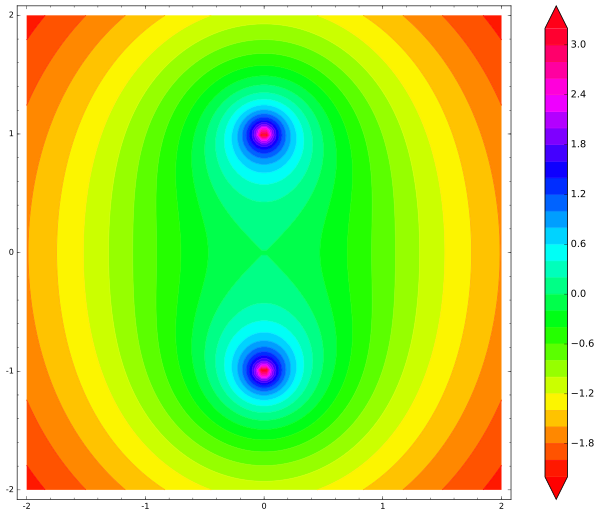
Bagaimana kita menggambarkan energi potensial tongkat kita? Tongkat memiliki tiga derajat kebebasan (dua untuk gerakan dan satu untuk rotasi), sehingga grafik akan empat dimensi. Mari kita abaikan rotasi untuk saat ini dan biarkan tongkat bergerak dari sisi ke sisi. Kami memperbaiki titik pada tongkat (misalnya, pusatnya) dan menggambar peta energi potensial tongkat untuk pusatnya. Dalam hal ini, energi potensial total tongkat adalah jumlah energi potensial dari muatannya pada kedua ujungnya:

 var('x,y') def unit_potential(a,b,x,y): return -ln(sqrt((xa)^2 + (yb)^2)) def system_potential(x,y): return unit_potential(0,1,x,y)+unit_potential(0,-1,x,y) def energy(x,y): return system_potential(x+2,y)+system_potential(x-2,y) contour_plot(energy(x,y), (x, -3, 3), (y, -2, 2), cmap='hsv', contours=30, figsize=12, colorbar=True) 

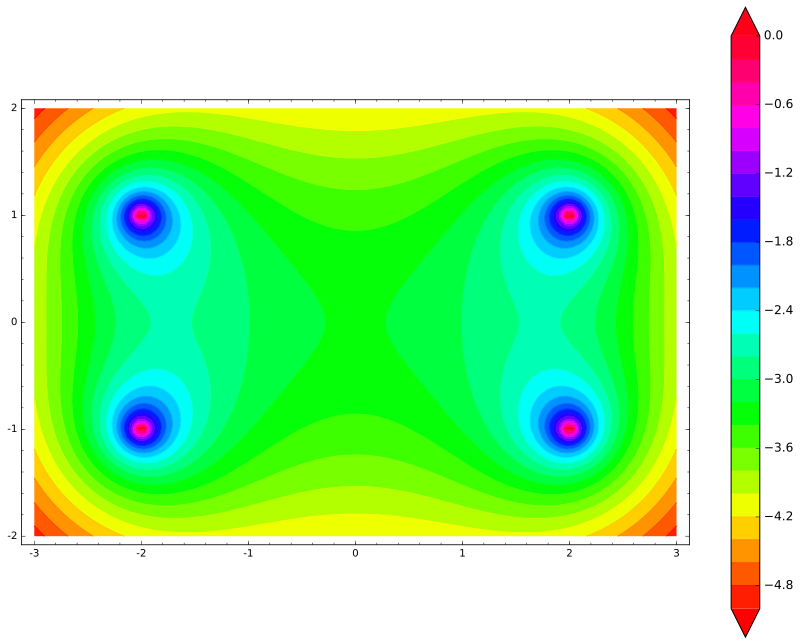
Jadi, energi tongkat memiliki empat puncak (masing-masing ujung dapat mengenai masing-masing dari dua muatan). Seperti yang diharapkan, tongkat tidak akan bergerak secara horizontal - sebagai gantinya, tongkat akan bergerak secara vertikal!

Itu hanya logis, karena bagaimana kita mendapatkan energi? Kami menambahkan energi potensial dari setiap pengisian daya. Kita tahu bahwa energi potensial dari setiap muatan adalah fungsi nol-laplacian. Jumlahnya, karenanya, juga memiliki nol laplacian. Oleh karena itu, energi potensial dari setiap benda yang dibebankan (bukan hanya tongkat kita!) Tidak dapat memiliki minimum dalam medan listrik statis!

Kesimpulan

Gambar intuitif medan magnet dan listrik dari orang-orang yang tidak bekerja dalam fisika bisa menyesatkan. Otak kita membodohi kita dengan membuat gambar energi minimum. Sayangnya, tidak demikian halnya, dan membuat motor Mendocino tanpa dukungan mekanik sangat sulit, jika bukan tidak mungkin.

Celah apa yang ada untuk dieksploitasi? Teorema Earnshaw (jika kita menerapkannya pada magnet) hanya berlaku untuk sistem magnet statis yang tetap .

1. Kita dapat membuat medan magnet dinamis.
2. Diamagnetisme dan superkonduktor juga tidak termasuk dalam teorema Earnshaw.
3. Memindahkan (dan secara khusus, memutar) benda sama sekali tidak dibahas di sana, dengan levitron menjadi contoh paling terkenal.

Tidak, ini bukan tanpa harapan. Tentu saja, menggunakan celah ini akan membunuh estetika motor Mendocino, tetapi keajaiban benda logam yang melayang bebas akan mengalahkan semua itu!

Catatan terakhir: teorema Earnshaw-lah yang membuktikan tidak adanya zat padat, oleh karena itu membantah model atom yang diterima, yang mengarah pada model atom "planet".