Tingkat kesulitan membaca
Pengantar dan aturan main
Beberapa tahun yang lalu saya membeli game Dobble ( Dobble , nama aslinya adalah "Spot It!"). Ini adalah gim yang sangat sederhana, cepat dan menyenangkan, yang saya anggap sebagai salah satu gim papan terbaik pada umumnya.
Ada 55 kartu di set permainan dengan 8 simbol yang berbeda pada masing-masing. Seperti apa bentuknya kartu-kartu ini:

Fig. 1. Contoh kartu permainan.
Pada masing-masing dua kartu satu dan hanya satu simbol yang cocok. Pada gambar di atas, ini adalah simbol pensil:

Fig. 2. Mencocokkan karakter pada kartu.
Pemain yang pertama kali melihat pertandingan melakukan aksi pada salah satu kartu, tergantung pada putaran permainan. Misalnya, bawa ke dirinya sendiri atau lemparkan ke lawan.
Seringkali ini mengarah pada fakta bahwa salah satu kartu yang dicari pemainnya sedang berubah. Karena itu, Anda harus mencari pasangan baru, yang mungkin merupakan simbol yang sama sekali berbeda:


Fig. 3, 4. Kartu pertama diganti dengan yang baru. Sekarang ada kebetulan baru di antara mereka - simbol badut.
Bagaimana mereka melakukannya?
Pada pandangan pertama, tampaknya sulit dipercaya bahwa pada dua kartu tepat satu kebetulan, tidak lebih, tidak kurang. Pertanyaan segera muncul - berapa banyak karakter yang ada dalam permainan? Mereka tidak boleh terlalu sedikit (maka akan ada lebih dari satu kecocokan pada kartu) atau terlalu banyak (maka mungkin tidak ada kecocokan pada kartu).
Selain itu, jelas bahwa simbol-simbol tersebut terletak pada kartu dalam urutan khusus, yang menjamin satu-satunya yang cocok untuk dua kartu.
Keterampilan dasar Google membawa kami ke situs web stackoverflow, yang menjelaskan mengapa hal ini terjadi: http://stackoverflow.com/questions/6240113/what-are-the-mathematical-computational-principles-behind-this-game
Permainan menggunakan prinsip-prinsip geometri terbatas . Meskipun ada kata "geometri" dalam frasa ini, konsep ini lebih mengacu pada kombinatorik daripada geometri. Ini beroperasi dengan sejumlah titik yang terbatas yang dapat ditemukan, khususnya, dalam bentuk bidang proyektif .
Kartu dan simbol dalam permainan adalah elemen dari bidang proyektif urutan ke-7. Ini berarti bahwa pada setiap kartu ada simbol n + 1 , dan jumlah total simbol unik dalam permainan adalah n ^ 2 + n +1 , yaitu 57 karakter.
Ada pesawat pesanan baik yang lebih rendah dan lebih tinggi. Misalnya, ada pesawat pesanan ke-5. Baginya, 6 simbol ditampilkan pada kartu, dan jumlah total simbol unik dalam permainan adalah 5 ^ 2 + 5 + 1 = 31. Pesawat proyektif dari konfigurasi ini digunakan dalam versi yang lebih sederhana dari permainan Doble yang disebut “Doble 1,2,3” .
Koneksi antara titik dan garis untuk bidang proyektif diatur menggunakan matriks kejadian . Penampilannya disajikan di bagian “Incidence matrix for the game Dobble”.
Geometri final untuk bayi
Jauh setelah menulis artikel asli, saya menghadiri kuliah oleh Alexei Savvateev , di mana ia berbicara tentang geometri projektif yang jauh lebih pendek dan lebih mudah dimengerti. Tetapi karena saya tidak memiliki kekuatan atau keinginan untuk menulis ulang setengah dari artikel karena hal ini, saya hanya merekomendasikan bukunya "Matematika untuk Kemanusiaan," jika upaya saya oleh orang biadab untuk menjelaskan perangkat mobil dengan jari tidak akan dapat dipahami atau membosankan.
Pertama, buka Wikipedia dan baca beberapa artikel. Artikel pertama menjelaskan konsep geometri terbatas:
Geometri terbatas adalah setiap sistem geometrik yang memiliki jumlah titik terbatas . [1]
Sejauh ini, semuanya sederhana. Jika Anda menggambar beberapa titik dengan pena di atas kertas, maka mereka akan membuat semacam geometri terbatas.
Kejutan menunggu lebih banyak lagi:
Sebagai contoh, geometri Euclidean tidak terbatas, karena garis Euclidean mengandung jumlah poin yang tidak terbatas, atau lebih tepatnya, mengandung poin yang persis sama banyaknya dengan bilangan real . [1]
Bagi kami, ini berarti bahwa selembar kertas di mana titik-titik kami digambar bukan bidang dalam hal geometri terbatas . Itu hanya pembawa titik.
Ada dua jenis geometri di pesawat: affine dan projective . Dalam geometri affine, gagasan paralelisme garis yang biasa digunakan. [1]
Ingat apa aksioma yang menggambarkan geometri affine:
Affine geometry pada pesawat adalah himpunan nonempty X (yang elemennya disebut "poin"), dengan koleksi himpunan bagian subset L yang kosong dari X (yang elemennya disebut "langsung"), sehingga:
- Untuk dua titik berbeda, hanya ada satu garis yang berisi kedua titik.
- Untuk garis ℓ dan titik p yang bukan milik ℓ , terdapat satu dan hanya satu garis ℓ ′ yang mengandung p sedemikian rupa sehingga ℓ ∩ ℓ ′ = ∅.
- Ada banyak dari empat poin, tidak ada yang terletak pada garis yang sama. [1]
Aksioma-aksioma ini memberi kita kesempatan untuk memahami seperti apa bentuk affine paling sederhana dalam geometri terbatas:
Pesawat affine paling sederhana hanya berisi 4 poin, dan disebut pesawat affine orde kedua . Setiap pasangan poin mendefinisikan garis yang unik, oleh karena itu bidang yang ditunjukkan berisi 6 garis. [1]
Tidak terlalu jelas? Benar juga. Jika Anda melihat dekat pada definisi geometri affine, Anda dapat melihat bahwa itu beroperasi dengan konsep teori himpunan (elemen, set, subset).
Ini berarti bahwa garis-garis mungkin tidak terlihat sama sekali seperti garis geometri Euclidean yang biasa.
Faktanya, itu benar. Jika Anda melihat gambar pesawat affine orde dua, kita akan melihat gambar berikut:

Fig. 5. Pesawat Athena orde kedua. (Sumber ru.wikipedia.org )
Titik-titik di sini terlihat seperti titik hitam biasa, tetapi garis lurus adalah segmen multi-warna. Garis dengan warna yang sama dianggap paralel.
Seperti yang Anda lihat, garis-garis di sini tidak panjangnya tak terbatas. Secara rahasia, saya akan mengatakan bahwa tidak ada konsep panjang sama sekali di sini, dan garis lurus dapat memiliki bentuk apa pun, seperti yang akan segera kita lihat.
Tentunya% username% masih ragu bahwa gambar dari pesawat ini memenuhi aksioma geometri affine. Mari kita periksa:
- Kami mengambil 2 poin, misalnya, kiri atas dan kiri bawah.
Kedua titik ini hanya mengandung satu garis merah kiri.
Garis merah kanan tidak mengandung salah satu dari titik-titik ini, dan garis yang tersisa hanya mengandung satu dari mereka. - Ambil garis lurus merah kiri dan titik kanan atas. Jelas, hanya satu garis lurus (merah kanan) yang sejajar dengan garis merah kiri, karena melewati titik kanan atas, tetapi tidak melewati salah satu dari dua titik kiri.
- Gambar tersebut dengan jelas menunjukkan bahwa tidak peduli apa pun 3 poin yang kita ambil, salah satunya terletak pada garis yang berbeda dari garis di mana kedua titik lainnya terletak.
Dua garis yang membentuk diagonal kotak tidak berpotongan, karena mereka tidak memiliki titik yang sama.
Jika Anda memahami dengan baik isi dari gambar sebelumnya, maka gambar itu lebih rumit:
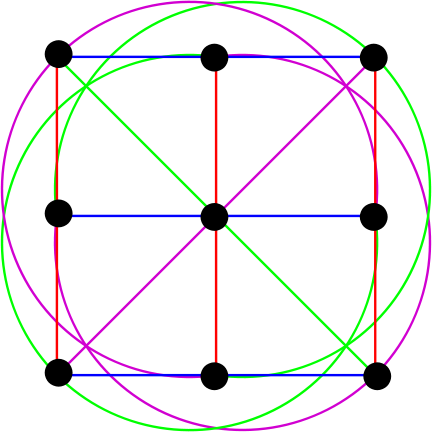
Fig. 6. Pesawat Athena dari urutan ketiga. (Sumber ru.wikipedia.org )
Di sini kita melihat 9 poin dan 12 garis. Ya,% nama pengguna%, elips ini sebenarnya garis lurus dalam hal geometri terbatas.
Bentuk warna yang sama adalah garis paralel. Sulit untuk diperhatikan, jadi kami membagi gambar menjadi beberapa:
| Pesawat nomor 1 | Nomor pesawat 2 | Pesawat nomor 3 | Nomor pesawat 4 |
|---|
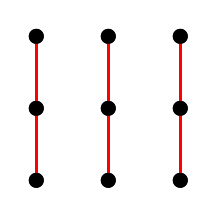 | 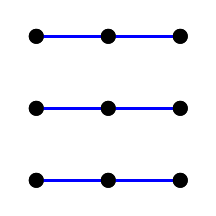 |  |  |
Fig. 7. Garis lurus paralel dari bidang affine orde ketiga.
Di sini, memeriksa eksekusi aksioma akan memakan waktu sedikit lebih lama:
- Kami mengambil 2 poin, misalnya, tengah atas dan kanan bawah. Melalui mereka hanya melewati salah satu garis ungu.
- Ambil garis merah kiri dan titik kanan bawah. Sama halnya dengan pesawat orde kedua, hanya satu garis merah kanan melewati titik ini, tetapi tidak melewati salah satu dari tiga titik kiri.
- Ini sedikit lebih rumit daripada dalam kasus pesawat orde ke-2. Pernyataan aksioma mengatakan bahwa Anda perlu menemukan setidaknya satu set empat poin (tidak kosong), di mana tidak ada tiga terletak pada lebih dari satu baris.
Jelas, 12 set dengan tiga titik di mana garis-garis dalam gambar melewati tidak memenuhi kondisi ini. Tapi itu memuaskan, misalnya, satu set empat titik sudut.
Dalam kasus yang lebih umum, bidang hubungan berhingga terbatas n memiliki n ^ 2 poin dan n ^ 2 + n garis; setiap baris berisi n poin, dan setiap titik milik n +1 baris. [1]
Dengan geometri affine selesai, kita beralih ke tipe geometri kedua pada bidang - proyektif.
Dalam geometri projektif, sebaliknya, dua garis berpotongan pada satu-satunya titik yang mungkin, dan oleh karena itu garis paralel tidak ada. [1]
Kalimat sebelumnya menjelaskan aksioma kedua geometri projektif. Yang pertama dan ketiga sama dengan di Athena.
Karena aksioma ketiga membutuhkan keberadaan setidaknya empat titik, bidang harus mengandung setidaknya 7 poin untuk memenuhi kondisi dari dua aksioma pertama. Dalam pesawat proyektif paling sederhana ini ada juga 7 garis; setiap titik memiliki tiga garis, dan setiap garis berisi tiga titik. Pesawat proyektif semacam itu sering disebut "pesawat Fano . " [1]
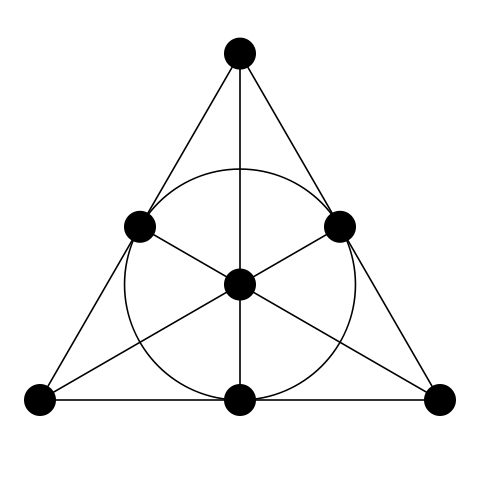
Fig. 8. Pesawat Fano. (Sumber en.wikipedia.org )
Dalam gambar ini, sulit untuk segera memahami semua 7 baris, jadi di sini adalah versi kuda dari bidang yang sama:
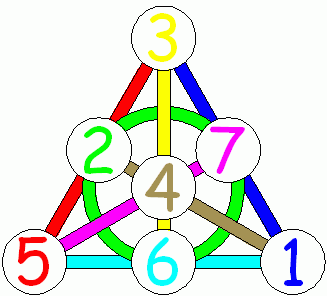
Fig. 9. Pesawat Fano dengan garis-garis berwarna. (Sumber mathpuzzle.com . Digunakan dengan izin dari Ed Pegg Jr. )
Jadi, pesawat Fano adalah pesawat proyektif 2-urutan dengan 7 poin dan 7 garis.
Apa hubungannya dengan kartu itu?
Apa yang terjadi jika kita merumuskan 2 aksioma geometri terbatas , mengganti "garis" dengan "simbol" dan "titik" dengan "kartu"?
Hasilnya adalah ini:
- Untuk dua kartu yang berbeda, hanya ada satu simbol, yang ditunjukkan pada kedua kartu.
- Untuk dua simbol berbeda, hanya ada satu kartu yang berisi kedua simbol ini.
Sekarang, berdasarkan pengetahuan ini, mari kita lihat seperti apa Dobble dalam kasus yang paling sederhana. Ini akan memiliki 7 kartu dan 7 karakter, masing-masing kartu akan memiliki 3 karakter (karena 3 garis berpotongan pada satu titik):
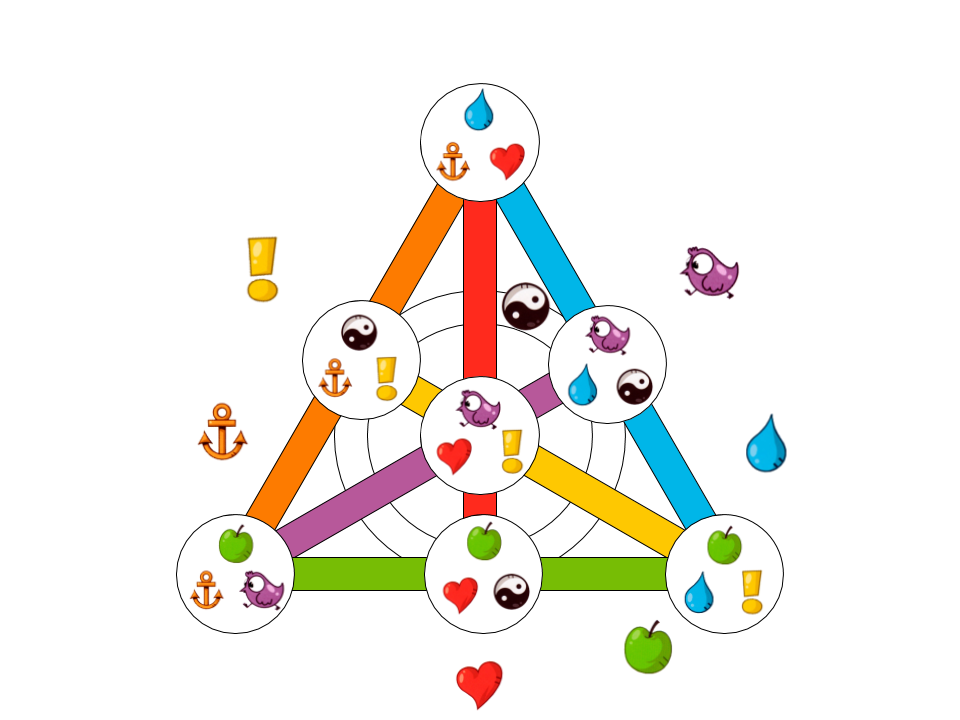
Fig. 10. Contoh set kartu sekecil mungkin untuk Dobble.
7 karakter berikut digunakan di sini:
 ,
,  ,
,  ,
,  ,
,  ,
,  ,
, 
Tidak peduli apa pun 2 kartu yang kita ambil, mereka akan memiliki simbol yang sama, digambarkan di sebelah garis di mana kedua kartu terletak.
Misalnya, kartu di sudut kiri bawah dan kartu di tengah sisi kanan memiliki simbol yang sama  . Ditampilkan di sebelah baris.
. Ditampilkan di sebelah baris.  .
.
Pesawat projektif pesanan kecil
Pada Wolfram Anda dapat menemukan demonstrasi visual dari pesawat proyektif pesanan kecil: http://demonstrations.wolfram.com/ProjectivePlanesOfLowOrder/
Ini dirancang sebagai dokumen dalam format CDF (Computable Document Format), untuk itu Anda perlu menginstal CDF Player .
Berikut adalah contoh bidang proyektif pesanan 3:
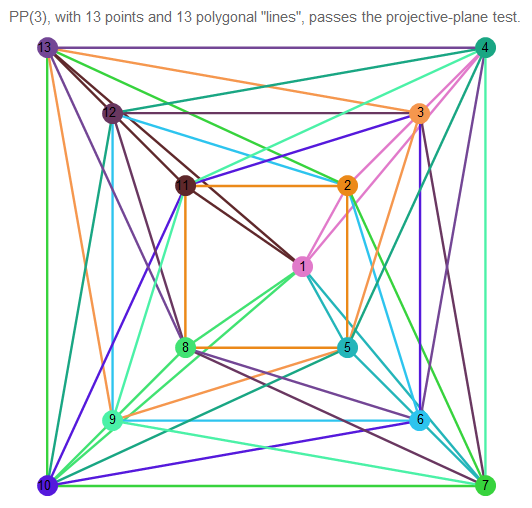
Fig. 11. Gambar bidang proyektif dari 3 pesanan.
Sulit untuk memahami apa yang terjadi, jadi ambil 2 garis arbitrer:
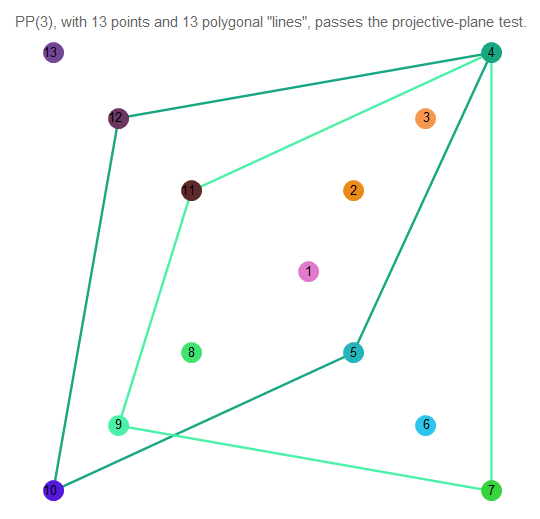
Fig. 12. Perpotongan dua garis bidang proyektif orde ke-3.
Seperti yang kita lihat, mereka berpotongan tepat pada satu titik. Garis itu sendiri mengandung 4 poin.
Untuk memastikan bahwa 4 baris melewati setiap titik, Anda harus mengganti pasangan garis yang ditampilkan dalam dokumen interaktif dan fokus pada beberapa titik.
Pesawat projektif dengan pesanan lebih tinggi ditunjukkan pada gambar di bawah ini.
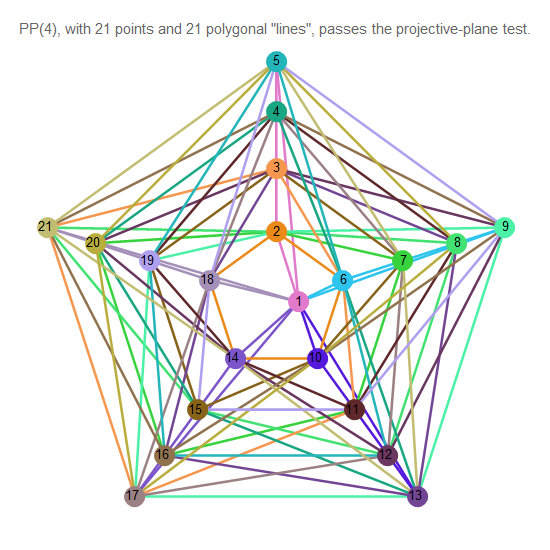
Fig. 13. Pesawat proyektif pesanan 4
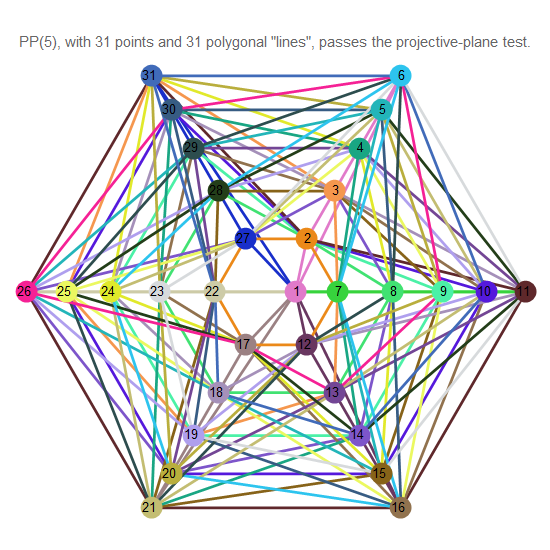
Fig. 14. Bidang proyektif pesanan 5

Fig. 15. Pesawat proyeksi 7
Dalam urutan di atas, tidak ada gambar untuk bidang proyektif urutan ke-6. Ini bukan kesalahan.
Meskipun Wolfram menghasilkan representasi grafis dari struktur seperti itu, itu tidak memuaskan aksioma geometri projektif, dan bukan bidang proyektif.
Diasumsikan, tetapi masih belum terbukti, bahwa urutan pesawat hingga selalu merupakan kekuatan utama . [1]
Bagaimana cara membangun pesawat proyektif?
Representasi grafis dari bidang proyektif terlihat menarik dan jelas, tetapi bagaimana menemukan kombinasi titik sehingga memiliki properti di atas?
Cara termudah adalah dengan mengunjungi situs-situs yang menampung data pra-perhitungan untuk pesawat projektif berbagai pesanan.
Misalnya, untuk bidang proyektif pesanan 7, Anda dapat mengunjungi halaman berikut: https://web.archive.org/web/20170619110638/https://www.uwyo.edu/moorhouse/pub/planes/pg27.txt
Matriks angka disajikan di sana. Garis adalah kartu (titik) dalam hal Dobble. Angka-angka dalam garis adalah nomor seri karakter (garis), mulai dari nol, yang digambarkan pada setiap kartu (melewati titik ini).
Anda juga dapat menggunakan layanan paket matematika, seperti Matlab, untuk membangun matriks kejadian dari bidang proyektif. [2] [3]
Matriks insiden
Matriks kejadian adalah salah satu representasi grafik yang menunjukkan hubungan antara elemen-elemen insiden dari grafik (edge (arc) dan vertex). Kolom matriks berhubungan dengan tepi, baris ke simpul. Nilai bukan nol dalam sel matriks menunjukkan hubungan antara titik dan tepi ( kejadiannya ). [2]
Salah satu contoh paling sederhana dari matriks kejadian dapat berupa matriks 2x1 untuk grafik dua arah yang tidak terhubung yang dihubungkan oleh satu sisi:

Fig. 16. Grafik dua arah yang tidak terhubung yang dihubungkan oleh satu sisi, dan matriks kejadiannya.
Contoh grafik dan matriks insiden yang lebih kompleks:
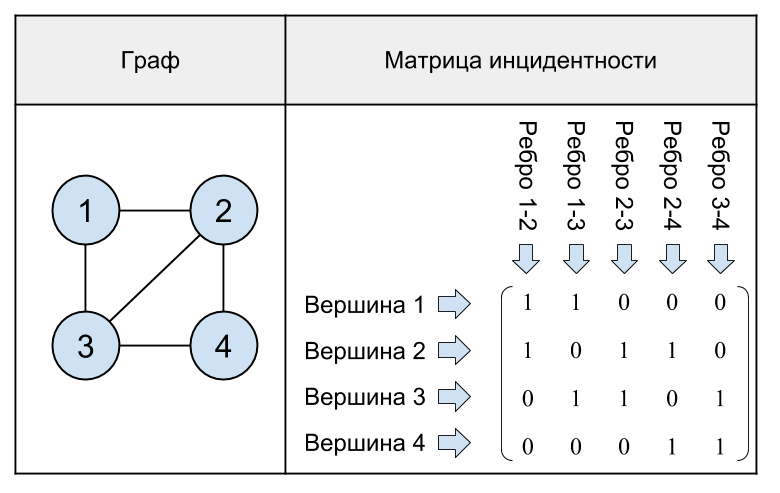
Fig. 17. Grafik tidak berarah dengan 4 simpul dan matriks kejadiannya.
Seperti yang dapat dilihat dari contoh terakhir, dalam matriks kejadian grafik di setiap kolom ada tepat dua unit, karena satu sisi menghubungkan dua simpul.
Bidang projektif adalah hypergraph , karena satu garis (tepi) menghubungkan beberapa titik (simpul). Oleh karena itu, dalam matriks kejadian bidang proyektif, unit di setiap kolom terjadi n + 1 kali, di mana n adalah urutan bidang proyektif.
Untuk bidang Fano ditunjukkan pada Gambar. 9, matriks kejadian adalah sebagai berikut:

Fig. 18. Matriks kejadian pesawat Fano.
Untuk menyederhanakan persepsi, nol tidak ditampilkan, dan unit digantikan oleh simbol X.
Dalam representasi bidang proyektif ini, prinsip dualitas titik dan garis terlihat jelas - garis melewati tepat 3 titik, dan, pada saat yang sama, titik tersebut memiliki tepat tiga garis.
Membangun pesawat proyektif dengan kekerasan
Pengetahuan saat ini tentang sifat-sifat matriks kejadian cukup untuk membangunnya untuk bidang proyektif dari setiap urutan n. Untuk melakukan ini, Anda dapat menggunakan pseudocode berikut:
n+1 , n+1 , ,
Dengan mengikuti algoritma ini, kami memperoleh matriks simetris untuk bidang Fano:

Fig. 19. Matriks insiden bidang Fano dibangun oleh algoritma pseudo-code.
Matriks ini tidak cocok dengan yang sebelumnya. Faktanya, itu tidak masalah.
Permutasi dari dua baris matriks kejadian sama dengan memberi nama baru pada simpul grafik.
Permutasi dari dua kolom matriks kejadian sama dengan memberi nomor baru pada tepi grafik (jika diberi nomor terlebih dahulu).
Matriks Insiden untuk Dobble
Untuk permainan Dobble dalam matriks kejadian, baris bertanggung jawab atas kartu, dan kolom bertanggung jawab atas karakter pada kartu tersebut.
Dengan demikian, permutasi dari dua kolom dari matriks kejadian sama dengan perubahan urutan karakter pada kartu. Namun, simbol pada kartu tidak terurut, sehingga operasi ini tidak mempengaruhi tampilan kartu.
Pengaturan ulang dua garis berarti bahwa pada semua kartu dua simbol yang sesuai saling menggantikan.
Operasi terakhir mengubah tampilan kartu, yang berarti bahwa rangkaian karakter yang kita lihat dalam permainan hanyalah salah satu dari kombinasi yang mungkin.
Jumlah set karakter untuk kartu yang diberikan adalah kombinasi dari 57 elemen dan 8 elemen tanpa pengulangan. Itu dihitung dengan rumus 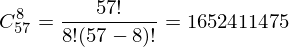
Matriks kejadian untuk Dobble ditunjukkan pada tabel di bawah ini. Ditransposisikan, mis. baris adalah simbol, dan kolom adalah kartu (gambar dapat diklik). Habr tidak memungkinkan Anda untuk menyisipkan gambar dengan ukuran dan kualitas yang diinginkan, sehingga opsi ukuran penuh adalah tautan terpisah: https://github.com/Skybladev2/DobbleMathModel/blob/master/images/Dobble%20incidence%20matrix.png

Fig. 20. Matriks kejadian dari permainan Dobble.
Dua kartu apa yang hilang dalam game?
Secara total, tabel dengan matriks kejadian permainan memiliki 57 baris dan 55 kolom. Ini berarti bahwa permainan dapat memiliki 2 kartu lagi.
Ini berarti bahwa karakter yang ada pada kartu-kartu ini kurang umum dalam permainan daripada yang lain. Jumlah karakter dalam game ditampilkan di kolom terakhir dari tabel.
Jumlah karakter dari kartu yang hilang adalah sebagai berikut:
 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  dan
dan 
(Total 14 karakter) terjadi 7 kali. terjadi 6 kali.
terjadi 6 kali.
Seperti apa kartu yang hilang itu? Untuk menjawab pertanyaan ini, ambil salah satu karakter di atas dalam matriks kejadian (kecuali untuk manusia salju), dan letakkan di kartu yang hilang (misalnya, kolom kedua dari belakang).
Kemudian kami menemukan semua kartu (kolom) di mana simbol ini digambarkan. Ini berarti bahwa pada semua kartu ini simbolnya bertepatan, dan tidak ada kecocokan lainnya.
Karena kartu-kartu ini sudah memiliki kecocokan dengan karakter yang dipilih, coret dari kolom kedua dari belakang semua karakter yang muncul di kartu lain.
Karakter yang hilang yang belum ditemukan, dan membentuk karakter dari salah satu kartu yang tersisa. Karena mereka ternyata persis 8, jenis kartu kedua yang hilang ditentukan secara unik.
Inilah 2 kartu ini:


Fig. 21. Jenis kartu yang mungkin hilang adalah No. 56 dan No. 57.
Tetap menjawab pertanyaan terakhir - apakah tidak adanya kartu ini memengaruhi properti kebetulan satu simbol antara dua kartu (mis. Tiba-tiba tidak ada kecocokan antara kartu apa pun)?
Jawabannya jelas, jika Anda masih melihat matriks kejadian permainan - tidak, tidak. Antara dua kartu (kolom) masih merupakan satu-satunya kebetulan.
Mengapa ada 2 kartu yang kurang dari jumlah maksimum yang dimungkinkan dalam permainan?
Awalnya, aturan untuk lima mini-game tidak ada dalam buklet, tetapi pada lima kartu terpisah. Pada saat yang sama, hanya 60 kartu yang dapat dicetak. Oleh karena itu, penulis permainan memutuskan untuk mengeluarkan 2 kartu, sehingga pada akhirnya ternyata 55 kartu dengan simbol + 5 kartu dengan aturan. (Terima kasih khusus kepada Guillaume Gille-Naves untuk klarifikasi.)
Ucapan Terima Kasih
Saya mengucapkan terima kasih kepada jaringan toko permainan papan “Igroved” atas bantuan mereka dalam menulis artikel.
Terima kasih kepada Ed Pegg Jr karena memberikan gambar pesawat Fano.
Secara terpisah, saya ingin menyebutkan satu anonim dan Guru untuk bantuan dalam memeriksa artikel.
Saya berterima kasih kepada toko "Table City" atas bantuan mereka dalam mempersiapkan publikasi artikel.
Dengan sepenuh hati saya berterima kasih kepada penulis game Igor Polouchine, Denis Blanchot, Guillaume Gille-Naves, serta Asmodee untuk hak menggunakan gambar dari game.