Terner seimbang
Saya sedang mengerjakan kuliah prinsip arsitektur komputer untuk universitas kami; dan sebagai tugas saya ingin mengusulkan kepada siswa saya untuk membangun mesin yang dapat diprogram sederhana yang bekerja di
ternary . Alasan utamanya adalah menyenangkan: sebagai dosen saya harus membawa sedikit hiburan, kalau tidak saya tidak akan didengarkan. Selain itu, penting untuk alasan historis. Lebih jauh "mengapa?!" pertanyaan akan dijawab "Karena saya bisa."
Halaman ini menjelaskan dasar-dasar yang sangat mendasar, ia tidak akan melampaui pengiklan ternary sederhana (dan implementasi perangkat kerasnya). Nantikan lebih lanjut.
Saya memilih sistem terner seimbang: setiap trit mewakili satu dari tiga kemungkinan keadaan, -1, 0 atau 1. Deskripsi yang sangat luas dari sistem ini dapat ditemukan di
sini .

Blok bangunan dasar: multiplexer ternary
Abstraksi
Satu-satunya blok yang akan digunakan di komputer saya adalah multiplexer ternary.
Itu dapat dilihat sebagai kotak hitam dengan lima pin: pin pemilih menerima sinyal ternary (baik -1, 0 atau 1), dan kemudian ada sedikit saklar di dalam kotak yang menghubungkan pin output dengan salah satu dari tiga pin input inN, inO atau inP.
Biasanya digambarkan seperti yang ditunjukkan di sini:
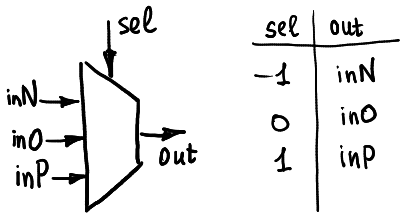
Demultiplexer ternary bekerja dengan cara yang sama: tergantung pada pin pemilih satu input terhubung dengan salah satu dari tiga pin output yang mungkin. Perhatikan bahwa di perangkat keras saya, saya menggunakan switch analog CMOS. Itu adalah dua arah, sehingga perangkat keras dapat digunakan baik sebagai multiplexer dan demultiplexer. Tapi bagaimanapun, untuk saat ini saya tidak menggunakan kemungkinan demultiplexing.
Implementasi perangkat keras
Desain dasar diusulkan oleh
Shaos .
Satu-satunya hal yang saya lakukan adalah membuat versi SMD dari TRIMUX. Sakelar dg403 permukaan mount dapat dibeli seharga 50 p per buah di Cina.
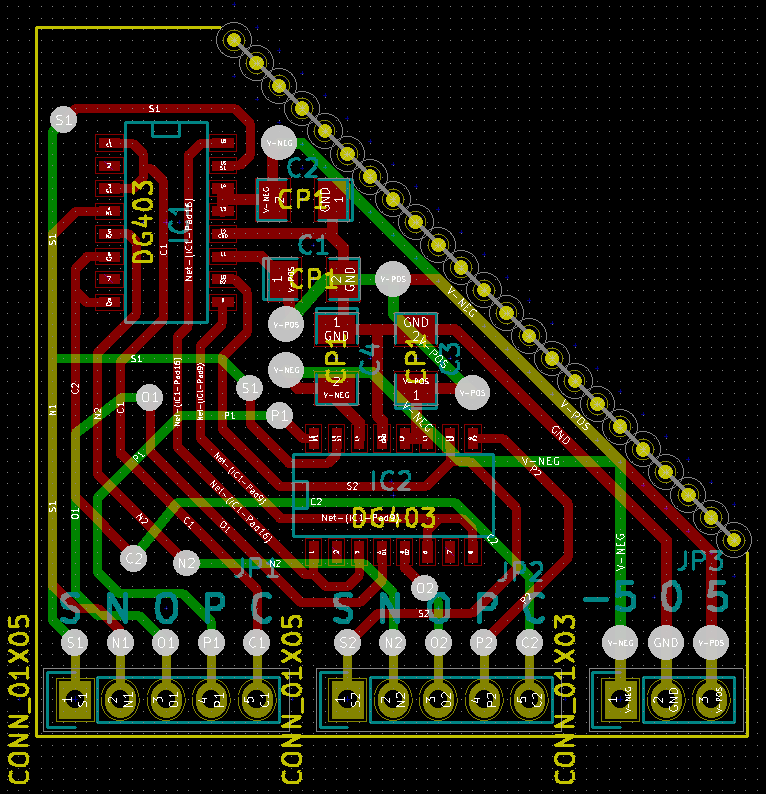
Sebelum saya menemukan desain ini saya mencoba menggunakan kombinasi cd4007 dan cd4016. Itu bekerja, tetapi perangkat kerasnya rumit dan jelek. Switch DG403 menyediakan kemungkinan komputasi terner sejati tanpa redundansi seperti menggunakan biner dua bit dan melarang salah satu dari empat konfigurasi.
Satu multiplexer ternary dapat dibuat dengan dua DG403: salah satu IC menerima input daya -5V ke 0V, sedangkan yang lain diberdayakan dengan 0V hingga 5V, dan memungkinkan penggunaan sinyal ternary yang diwakili oleh tiga tegangan -5V, 0V dan 5V, masing-masing. Desain ini hanya menggunakan setengah dari pin dg403, oleh karena itu wajar untuk membuat papan dengan dua multiplexer.
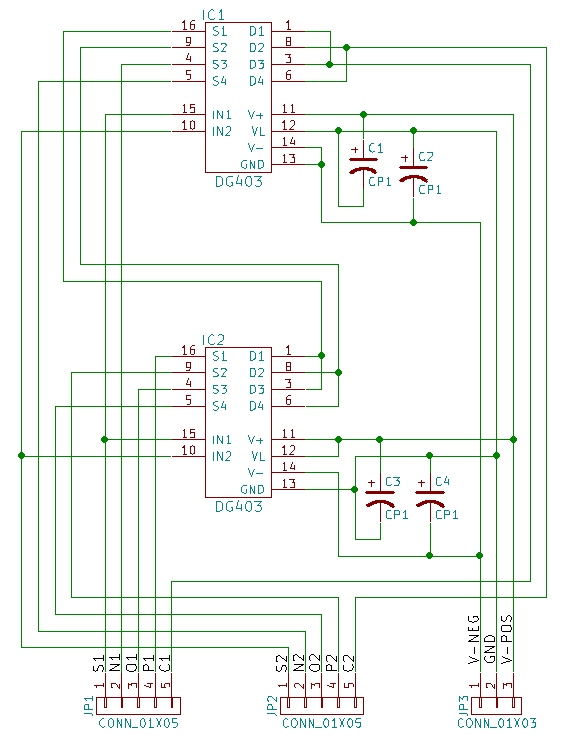
Jangan ragu untuk menghubungi Shaos di
sini . Pria yang luar biasa, alih-alih berspekulasi tentang manfaat ternary, ia merancang dan membuat IC ternarynya sendiri!

Bagaimana cara menggunakannya? Fungsi unary
Mari kita hilangkan fungsi identitas yang bisa kita peroleh dengan memberikan -1.0 dan 1 ke pin input yang sesuai dari multiplexer.
Untuk permulaan, mari kita tambahkan sinyal input A dengan menghitung A +1 (tentu saja, pada cincin -1,0,1):
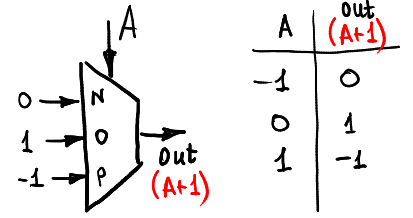
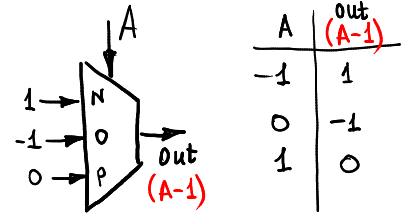
Berikut ini cara mengurangi input:
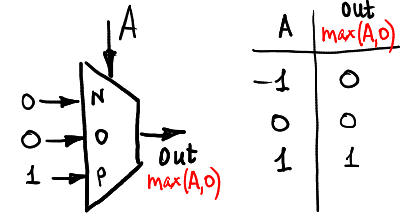
Mari kita hitung maks (A, 0):
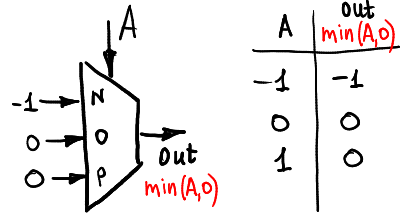
Dan min (A, 0):
Fungsi dua argumen: setengah penambah
A + B
Jadi, satu multiplexer memungkinkan kita untuk menghitung fungsi unary. Untuk menghitung fungsi dari dua argumen, kita perlu menggunakan tiga atau empat multiplexer. Misalnya, jika kita ingin menghitung jumlah dua sinyal A dan B (masih di ring -1,0,1), maka kita dapat menggunakan skema ini:
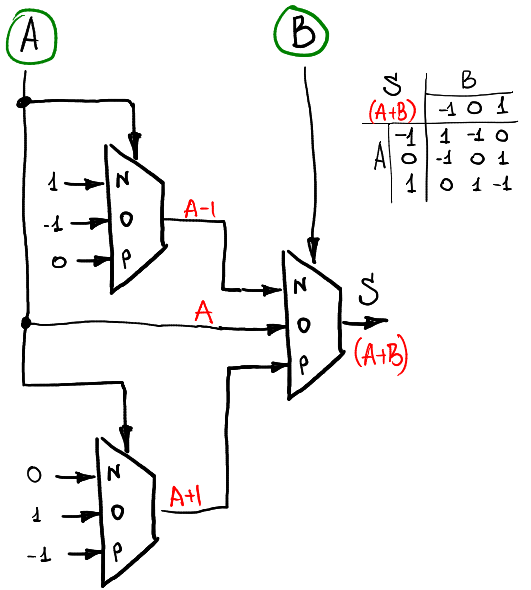
Ada dua lapisan multiplexer: yang pertama menghitung fungsi unary dari A, dan lapisan kedua menggabungkannya sesuai dengan B.
Konsensus
Jika kita ingin menghitung fungsi konsensus dari dua sinyal ternary (konsensus sama dengan -1 jika A = B = -1, sama dengan 1 jika A = B = 1 dan nol sebaliknya), maka kita dapat melakukannya seperti ini:
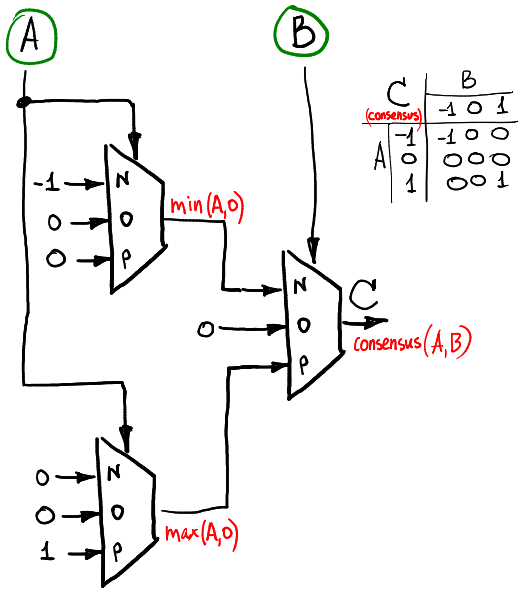
Implementasi perangkat keras
Bahkan, kami baru saja membuat
setengah penambah . Untuk dua input A dan B menghitung dua output S dan C terkait sebagai A + B = S + 3 * C. S adalah jumlah dan C adalah bendera carry.
Mari kita uji desainnya! LED Merah berarti -1, mati berarti 0, LED hijau berarti 1. Jadi, foto ini memberi tahu kita bahwa S = -1, C = 1, atau, dengan kata lain, 1 + 1 = -1 + 3 * 1:

Ini adalah tabel yang mencantumkan kesembilan kemungkinan status setengah penambah kami. Setiap sel memberikan nilai yang sesuai untuk S dan C. Tautan ke foto disediakan untuk setiap sel.
Tiga argumen: penambah lengkap
Berbeda dengan half-adder,
full-adder menerima tiga input A, B, Cin dan menghitung dua output S dan Cout terkait sebagai A + B + Cin = S + 3 * Cout.
Jumlah tiga trit
Jika kita ingin menghitung jumlah A + B + Cin, idenya sama dengan sebelumnya: kita menggunakan persiapan input lapis demi lapis. Lapisan pertama menerima A sebagai input, yang kedua menggunakan B dan lapisan multiplexer tunggal terakhir menggunakan Cin. Berikut adalah salah satu cara yang mungkin untuk menghitung output S:
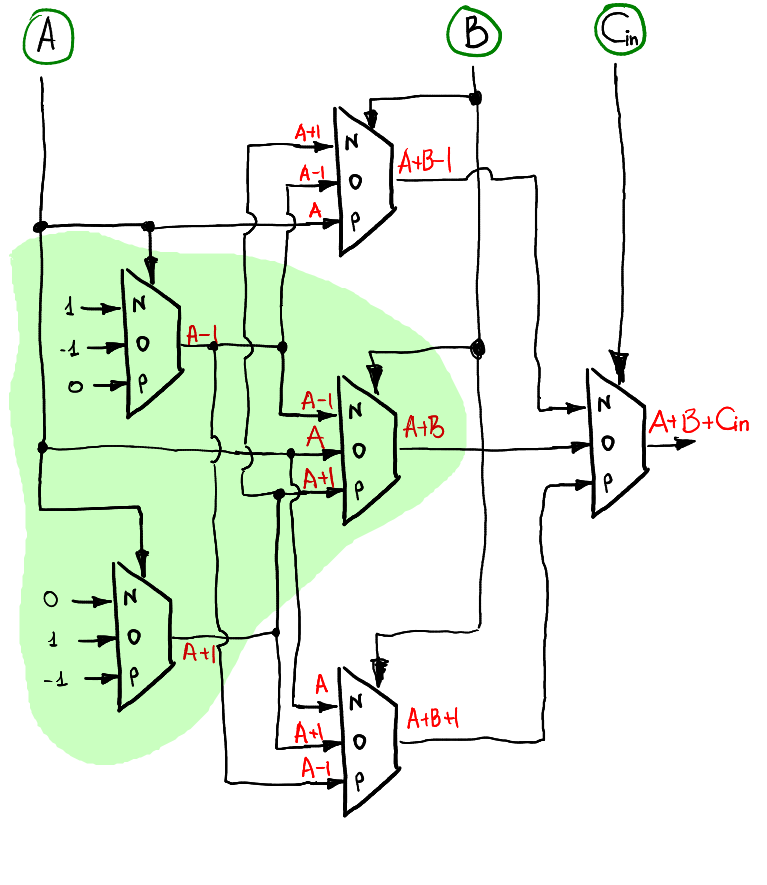
Perhatikan bahwa ketika Cin = 0, ia berperilaku persis dengan cara yang sama seperti half-adder, oleh karena itu wajar untuk melihat inklusi (disorot dengan warna hijau) dari skema half-adder di full-adder.
Overflow (carry flag)
Trit overflow dapat dihitung dengan cara lapis demi lapis yang sama. Ini juga termasuk setengah penambah!
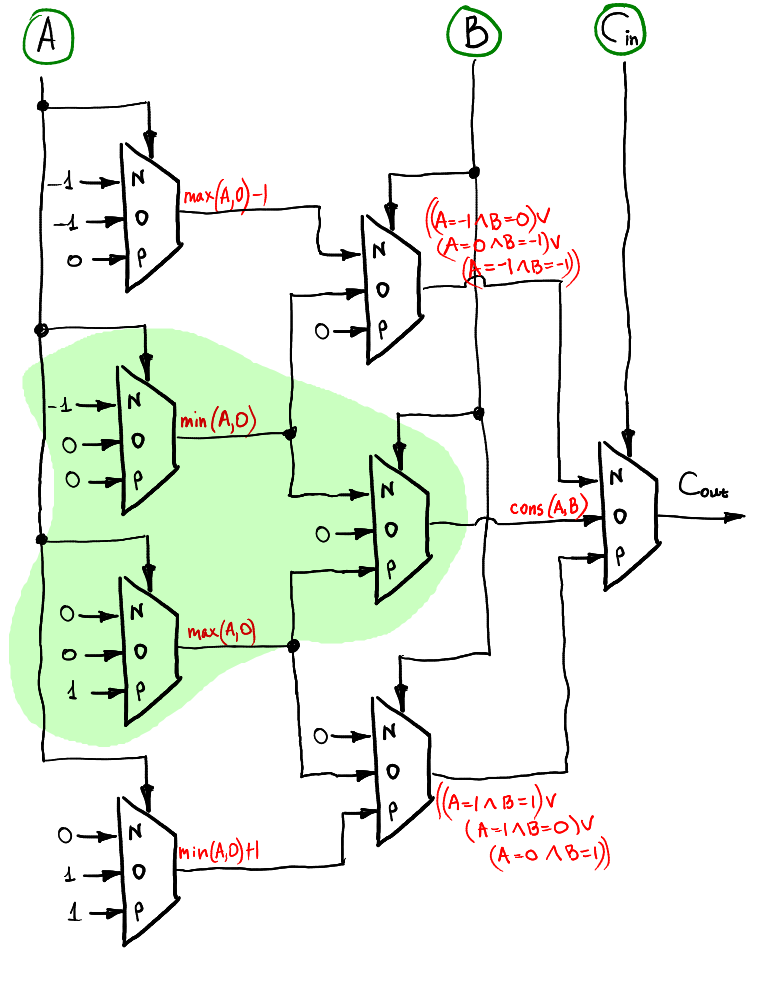
Validasi perangkat keras
Kali ini saya terlalu malas untuk menggunakan papan tempat memotong roti untuk menguji penambah penuh, jadi saya membuat PCB satu lapis ini:

Ini dia setelah tembaga terukir:

Tiga tabel berikut mencantumkan ke-27 kemungkinan status penambah lengkap. Seperti sebelumnya, foto-foto tersedia untuk setiap negara. Perhatikan bahwa tabel tengah (Cin = 0) persis sama dengan setengah penambah.
Keuntungan dari penambah penuh sehubungan dengan penambah setengah adalah kemungkinan untuk menumpuk banyak adders sampai kita mendapatkan cukup trit untuk mewakili jumlah yang kita inginkan.
Berikut ini adalah tumpukan dua adders:

Dan di sini cara memecahkan -4 + 2 (trit paling signifikan ada di sebelah kiri):

Tentu saja, kita tidak memerlukan papan penambah penuh untuk trit yang paling tidak signifikan (kita tidak perlu membawa bendera untuk input trit yang paling tidak signifikan), setengah penambah akan cukup.
Kesimpulan
Ini adalah akhir dari pengantar komputasi terner. Nantikan jam, penghitung, memori, dan lainnya!