Jadwal harian kebanyakan dari kita terbatas pada perjalanan dari rumah ke kantor dan kembali. Dan halangan paling sulit yang bisa memperlambat pergerakan kita adalah kemacetan lalu lintas. Tetapi di negara kita ada sejumlah besar tempat di mana Anda hanya bisa menggunakan kendaraan khusus.
Transportasi seperti itu baik jika Anda tidak perlu membawa kargo dalam volume besar atau bepergian ke daerah-daerah yang tidak dapat diakses seperti itu secara teratur. Maka kita harus sudah memikirkan membangun infrastruktur, pergerakan yang mungkin dilakukan pada angkutan sipil biasa.
Dan bagus jika seluruh kerumitan merancang rute masa depan terletak pada menemukan penggaris dan pensil untuk menggambar garis lurus pada peta yang menghubungkan beberapa objek. Tetapi, sayangnya, kenyataan kami sangat berbeda dari ini. Bagaimana jika medan yang terbang di atasnya menyerupai sepotong keju Swiss yang enak?

Selama lebih dari setahun, kami telah bekerja dengan rekan-rekan dari laboratorium penelitian Desain Digital untuk membuat alat yang dapat membangun berbagai jaringan komunikasi dalam mode otomatis. Untuk detailnya, selamat datang di kucing.
Bagaimana semuanya dimulai
Biasanya, perjalanan ke tempat-tempat terpencil seperti itu karena keuntungan finansial tertentu. Dan meskipun sering diketahui sebelumnya bahwa pengembangan daerah-daerah ini akan mendatangkan keuntungan yang baik, mengapa tidak menghemat uang untuk hal-hal yang dapat dilakukan tanpa kesulitan khusus? Bagaimana jika rute yang dirancang lebih kompeten memungkinkan kita untuk tidak membangun beberapa kilometer ekstra dari jalan raya?
Tetapi hanya ketersediaan jalan untuk menerima keuntungan yang signifikan jelas tidak cukup. Dan pada dasarnya itu hanya dibawa oleh deposit mineral. Oleh karena itu, selain jalan, perlu dirancang jaringan berbagai pipa, jaringan pipa air, jaringan saluran listrik dengan gardu listrik yang ditempatkan dengan benar. Semua infrastruktur ini dapat ditetapkan sebagai objek linear.

Dan ketika seorang insinyur dihadapkan dengan tugas mendesain jaringan komunikasi di lapangan dengan kondisi teknik dan geologi yang kompleks, tugas analitis yang sangat kompleks menjadi tanggung jawabnya.
Bagaimana tidak masuk ke zona banjir sungai? Bagaimana cara meminimalkan lintasan pada tanah permafrost? Bagaimana cara menghemat jumlah bantal pasir saat meletakkan jalan melalui rawa? Di mana mendapatkan pasir untuk bantal ini?
Ini hanya sebagian kecil dari pertanyaan yang diajukan seorang insinyur pada dirinya sendiri selama bekerja, namun Anda masih perlu mempertimbangkan berbagai GOST dan SNIP. Dan yah, jika Anda ingin menghubungkan hanya dua objek, dan jika ada beberapa lusin objek?
Oleh karena itu, industri desain sangat membutuhkan alat yang dapat menghitung biaya objek linear yang dirancang oleh seorang insinyur dan kemampuan untuk membangunnya dalam mode otomatis.
Data
Hal pertama yang harus kami tangani saat memulai tugas adalah pencarian data. Data apa yang dibutuhkan? Di mana mendapatkannya? Dan jika pertanyaan kedua dapat diselesaikan dengan bantuan pengguna, maka untuk memahami pertanyaan pertama kami membutuhkan analitik yang serius.
Dan data untuk perhitungan yang benar sangat membutuhkan banyak hal - mulai dari penandaan yang paling dangkal dari daerah di mana danau dan sungai ditandai, berbagai rawa, serta daerah karst, di mana sangat disarankan untuk tidak membangun karena ancaman kehancuran. Oleh karena itu, selain area yang dapat dilihat dari satelit, data dari studi geologi area juga diperlukan di sini.
Tetapi tidak semua data terbatas pada benda-benda alami di negara kita. Ada juga banyak hal yang diciptakan oleh manusia. Misalnya, dalam hal pembangunan jalan, kita dapat menggunakan jalan yang dibangun sebelumnya. Namun dalam pembangunan jaringan pipa, penggunaan infrastruktur yang ada jauh dari selalu mungkin. Karena koneksi pipa baru ke jaringan yang ada mungkin tidak lulus perhitungan hidrolik.
Selain menggunakan kembali apa yang sebelumnya dibuat oleh manusia, kita juga harus mempertimbangkan berbagai pembatasan pada konstruksi di dekat benda apa pun. Misalnya, untuk pembangunan saluran listrik, Anda perlu memperhitungkan indentasi dari tempat tinggal manusia tergantung pada tegangan pada saluran listrik itu sendiri.
Tetapi tidak sepenuhnya benar untuk mempertimbangkan perhitungan masalah hanya pada pesawat, karena selain dataran datar, ada daerah dengan perbedaan besar dalam ketinggian, di mana konstruksi juga tidak dapat dilakukan.
Mendapatkan data di medan adalah proses yang jauh lebih sederhana daripada data tentang penandaan area dan infrastruktur yang ada. Untuk menyederhanakan pengembangan, kami menggunakan data elevasi SRTM (Shuttle Radar Topography) terbuka yang dapat diperoleh siapa saja.

Jadi, kami memiliki data, kami tahu di mana kami bisa membangun, di mana kami tidak bisa membangun, ada biaya konstruksi untuk berbagai bidang medan. Kami memiliki kawasan, ia memiliki serangkaian objek yang ingin kami sambungkan ke jaringan komunikasi tunggal. Dalam istilah matematika, ini akan terdengar seperti pencarian solusi untuk masalah Steiner.
Sedikit matematika
Diketahui bahwa setiap formula membagi dua jumlah pembaca, jadi kami secara dramatis mengurangi bagian ini ...
Untuk mengoptimalkan rute fasilitas linier yang dirancang, perlu untuk dapat menghitung biaya konstruksinya. Setiap objek linier dapat direpresentasikan sebagai polyline L = \ {A_i, B_i \} _ {i = 0} ^ nL = \ {A_i, B_i \} _ {i = 0} ^ n terdiri dari segmen-segmen ABi .
Biaya konstruksi setiap bagian lurus dapat direpresentasikan sebagai nilai fungsi CABi , di mana setiap segmen ditentukan secara parametrik:
$$ display $$ {\ displaystyle AB_i \ colon \ left \ {{\ begin {align}} & s = s \ kiri (t \ kanan) - \ mbox {kurva parameter}, \\ & h = h \ kiri (s (t ) \ kanan) - \ mbox {fungsi ketinggian ketinggian}, \\ & c = c \ kiri (s (t) \ kanan) - \ mbox {fungsi biaya unit konstruksi pada suatu titik}, \\ \ end {sejajar}} \ kanan .} $$ tampilkan $$
dimana
t di kiri[0,1 kanan] - parameterisasi segmen.
CABi= int limitABic kiri(s(t) kanan) sqrt kiri[gxy(s(t))+ frac partialh partialsx cdot frac partialh partialsy kanan] dotsx dotsydt dimana g - tensor metrik permukaan Bumi tanpa memperhitungkan kelegaannya, yaitu, dengan kata-kata sederhana, fungsi mengukur jarak pada permukaan Bumi.
Karena fakta bahwa planet kita memiliki bentuk geoid, maka perlu menggunakan formula khusus untuk mengukur jarak. Untuk ini kami menggunakan rumus Haversinus. Di dalamnya, bentuk planet ini terlihat seperti bola, tetapi ini cukup untuk tujuan kita, karena kesalahan pengukuran sekitar 0,3% , dan kecepatan jarak perhitungan dengan metode ini tetap tinggi.
Pendekatan untuk Menemukan Cara Terbaik

Tetapi sebelum pindah ke bergabung dengan sekelompok objek, Anda perlu belajar bagaimana menemukan jalur optimal antara keduanya. Dua cara untuk melakukan ini segera muncul dalam pikiran:
- buat grafik, lalu terapkan metode pencarian jalur terpendek;
- gunakan solusi berdasarkan metode optimasi.
Saat menerapkan metode pertama, kami memiliki masalah yang terkait dengan metode pembuatan grafik untuk mendapatkan akurasi setinggi mungkin dari solusi. Penting untuk menemukan keseimbangan antara jumlah simpul dan tepi pada grafik, kualitas solusi, dan waktu yang dibutuhkan untuk menghitungnya.
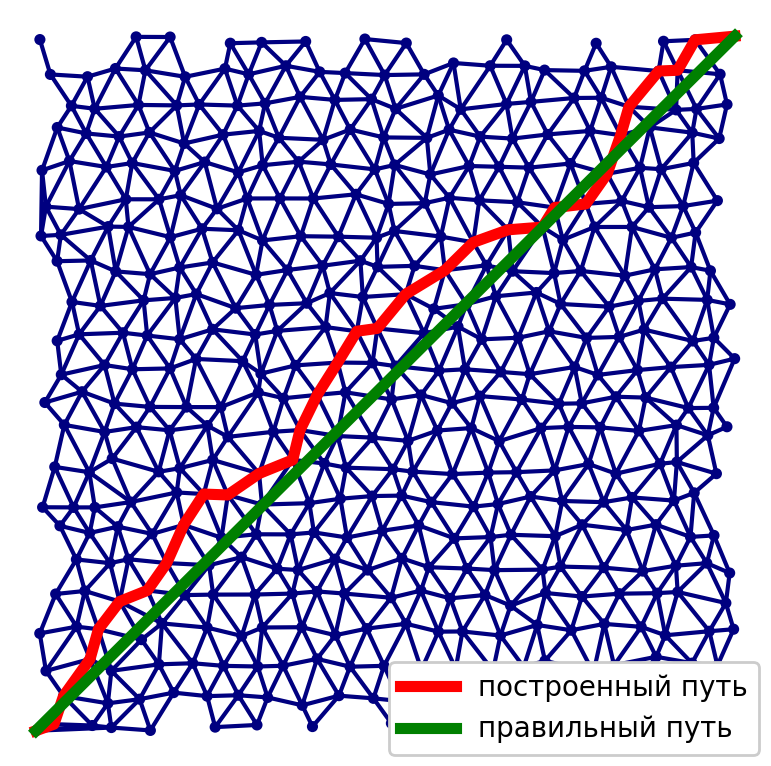
Dalam kasus kedua, masalah utama adalah minimum lokal. Sangat mudah untuk memilih kasus di mana solusinya mungkin tidak menyatu atau jauh dari optimal. Karena solusi yang diperoleh dengan metode ini sangat tergantung pada perkiraan awal. Jika kita memiliki perkiraan awal yang baik, maka hasilnya akan berkualitas tinggi.
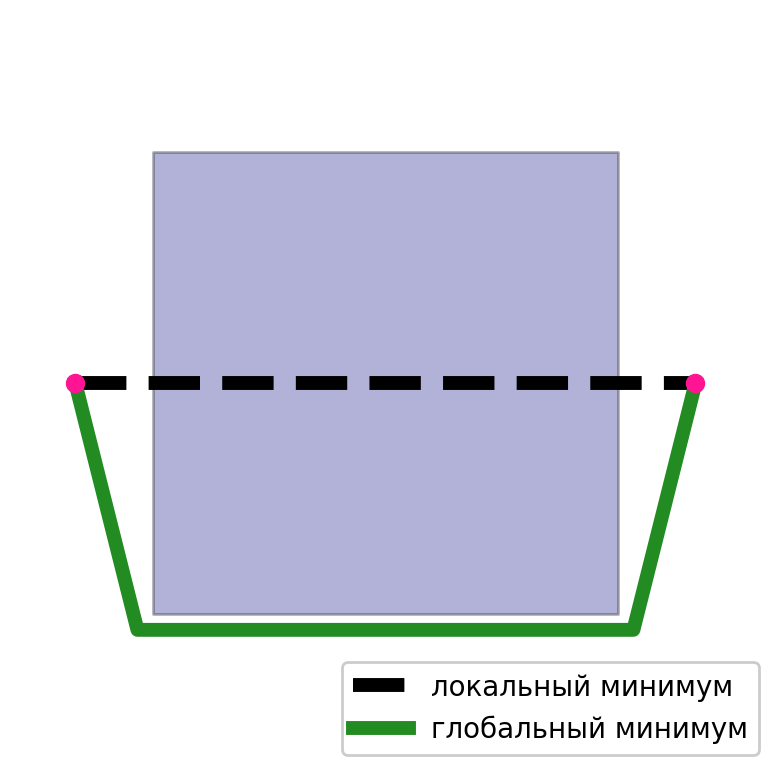
Jadi, kami memiliki dua pendekatan untuk menyelesaikan masalah ini. Yang pertama memiliki kualitas yang agak rendah, tetapi tidak ada masalah minimum lokal. Yang kedua memiliki masalah minimum lokal, tetapi solusi berkualitas tinggi. Dan jika Anda menggabungkan dua pendekatan ini dengan benar, maka kekurangan masing-masing akan hilang. Kami mengambil solusi yang diperoleh pada grafik sebagai perkiraan awal, dan kemudian menerapkan metode optimasi untuk itu.
Pada bagian artikel ini, kami akan mempertimbangkan dengan tepat solusi yang diusulkan untuk masalah ini pada grafik.
Pemilihan alat
Sebuah rencana aksi telah diuraikan, hanya tinggal "kode" saja. Karena pada tahap awal penulisan aplikasi, kami hanya memiliki sedikit pengetahuan tentang bidang subjek, kami membutuhkan bahasa yang fleksibel sehingga dalam kasus beberapa kesalahan perhitungan arsitektur, kami akan menulis ulang seluruh kode untuk beberapa kaleng bir malam. Saya juga secara opsional menginginkan perpustakaan untuk semua kesempatan, agar tidak menggunakan penemuan sepeda. Oleh karena itu, Python dipilih sebagai bahasa pemrograman utama.
Dalam aplikasi, kami menggunakan tumpukan teknologi yang mengesankan, yang tidak terbatas pada yang berikut:
- rupanya untuk bekerja dengan data geometris seperti poligon dan polyline;
- geopanda untuk pekerjaan yang nyaman dengan rupawan ;
- Scipy untuk menyimpan grafik yang dihitung dan menemukan jalur terpendek di atasnya, serta menemukan pohon rentang minimum;
- PyTorch untuk bekerja dengan fungsi biaya;
- bantal untuk bekerja dengan gambar.
Implementasi
Modul ini dapat dibagi menjadi beberapa tahap:
- generasi fungsi biaya;
- generasi grid komputasi;
- membangun grafik berdasarkan kisi;
- bobot grafik;
- perhitungan jalur terpendek pada grafik.
Karena tepi grafik adalah segmen, kita dapat menimbang sisi ini dengan menghitung nilai integral tertentu, yang disajikan di atas. Tetapi ada banyak sisi dalam grafik, dan, karenanya, nilai-nilai biaya dan ketinggian perlu diperoleh untuk sejumlah besar poin, yang bisa memakan banyak waktu.
Awalnya, idenya adalah untuk menemukan biaya satuan konstruksi dengan menentukan apakah suatu titik termasuk dalam poligon. Tetapi ide ini dicatat karena kompleksitas algoritmik yang tinggi dari pendekatan ini, karena mungkin ada banyak poligon, dan masing-masing dari mereka memiliki sejumlah besar simpul.
Oleh karena itu, untuk mengatasi masalah ini, kita dapat mewakili semua poligon yang kita miliki dalam bentuk gambar, yang dalam bentuk matematika adalah sebuah matriks. Dengan demikian, kita bisa mendapatkan biaya unit konstruksi pada titik di luar O (1) , dan oleh karena itu kita bisa mendapatkan biaya membangun tulang rusuk tertentu dengan akurasi tinggi.
Sekarang kita siap untuk membuat grafik, tetapi tidak ada cara unik yang benar untuk membangunnya untuk mendapatkan solusi presisi tinggi. Untuk membangun grafik, perlu untuk menghasilkan grid komputasi, yaitu, satu set titik di wilayah yang dipertimbangkan, terhubung dalam urutan yang sesuai dengan segmen yang membentuk wajah sel. Kisi dapat dibagi menjadi dua jenis: seragam dan tidak rata.


Model grid seragam menggambarkan koordinat masing-masing titik, sehingga jarak antara node grid sama. Kisi yang tidak rata muncul sebagai kumpulan poin individual secara acak .
Menggunakan kisi yang seragam tidak akan selalu memberikan hasil berkualitas tinggi untuk menemukan jalur terpendek, oleh karena itu, perlu untuk menguji pendekatan ini pada kisi yang tidak rata. Yang paling serbaguna adalah mesh segitiga.
Grid dihasilkan dengan memasukkan noise dengan koefisien tertentu ke dalam grid persegi panjang yang seragam, dan kemudian menerapkan poin triangulasi Delaunay untuk set poin ini.
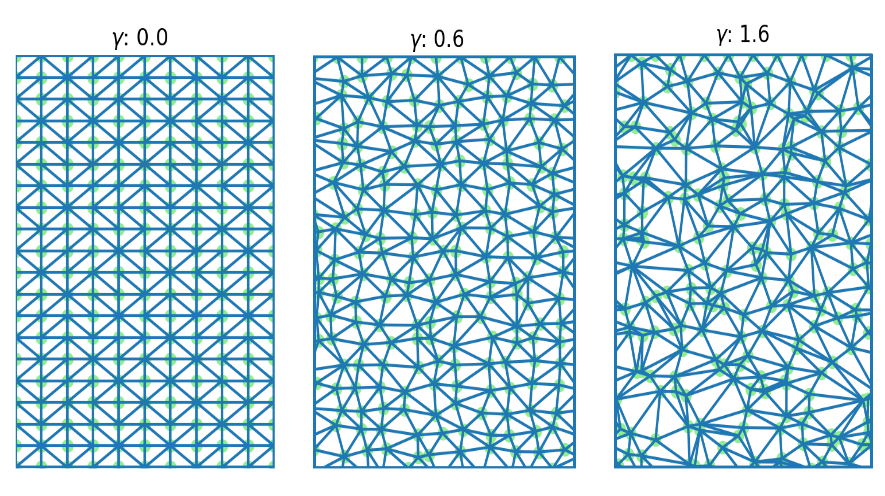
Efektivitas kisi-kisi yang dibangun diuji pada berbagai model peta wilayah, yang memperhitungkan berbagai biaya daerah dan bantuan, dan kemudian dilakukan perbandingan dengan solusi yang diperoleh secara analitik. Dengan mencari panjang tepi grafik dan koefisien memasukkan noise ke dalam grid yang seragam, parameter optimal ditemukan untuk membangun jalur optimal antara dua titik.
Masalah besar
Pada awalnya semuanya berjalan dengan baik, algoritma menghitung jaringan optimal, tetapi begitu ada masalah dengan kualitas jalur yang dibangun. Kasingnya cukup sederhana: Anda harus menghubungkan dua objek pada peta yang cukup panjang. Algoritma tidak ingin membangun rute yang jelas benar.
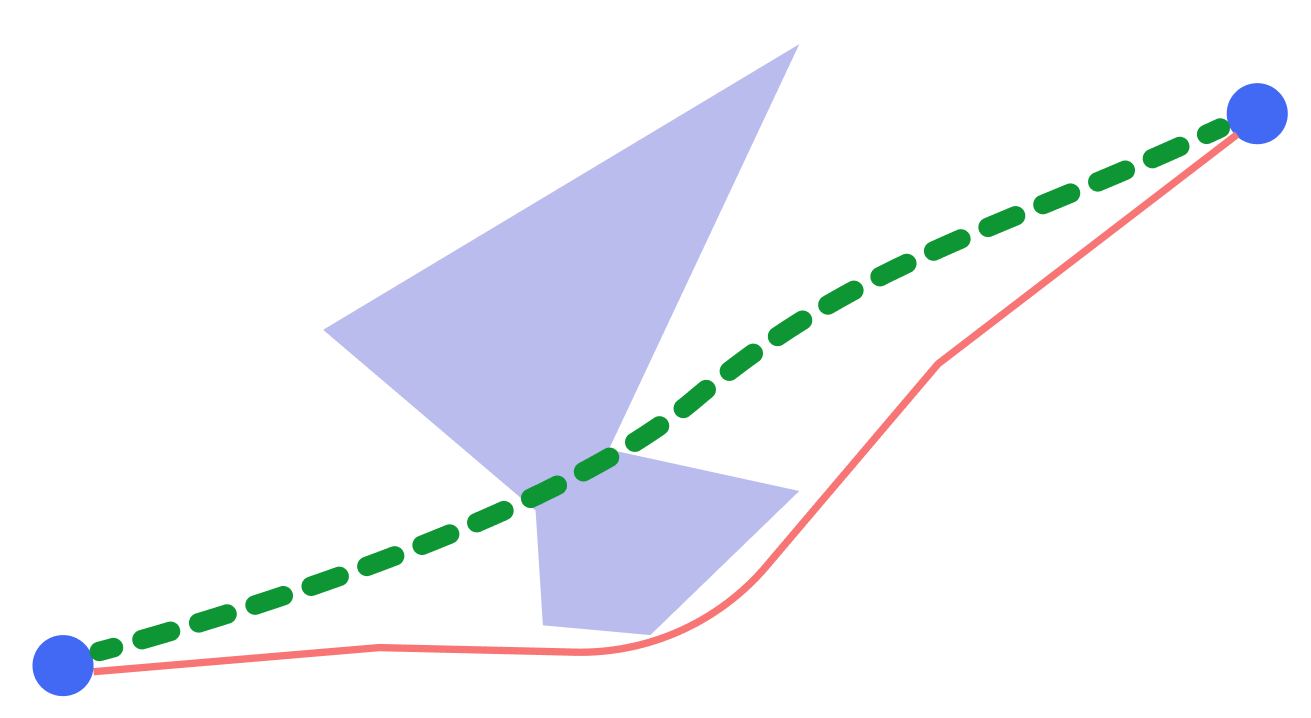
Masalahnya, seperti biasa, adalah dengan grid komputasi. Kami melanjutkan percobaan kami dengan tampilan kisi-kisi dan sampai pada kesimpulan bahwa menghubungkan simpul ke grafik, di mana setiap simpul terhubung ke tetangga terdekat, adalah solusi untuk masalah kami.
Jaringan
Setelah kami belajar bagaimana menemukan jalur optimal antara dua titik, langkah selanjutnya adalah memecahkan masalah membangun jaringan objek linear yang optimal. Algoritma yang ditemukan dalam literatur untuk membangun pohon Steiner pada grafik berorientasi pada masalah yang lebih umum, dan oleh karena itu tidak akan efektif dalam kasus kami. Grafik kami sangat jarang, dengan sejumlah kecil simpul terminal, relatif terhadap jumlah total simpul dalam grafik, dan tugas kami juga diterapkan. Oleh karena itu, untuk sejumlah alasan lain, diputuskan untuk mengembangkan algoritma kami sendiri yang menggunakan heuristik tertentu untuk secara efektif membangun jaringan yang optimal.
Deskripsi algoritma untuk membangun jaringan optimal pada grafik untuk kasus kami adalah topik untuk publikasi terpisah, kami tidak akan mempertimbangkannya di sini. Karena ketika menghitung tugas nyata, perlu memperhitungkan banyak kondisi tambahan dari industri konstruksi yang relevan bagi pengguna akhir, yang memberlakukan batasan tertentu pada algoritma yang digunakan.
Kasus nyata
Jadi, sekarang kita beralih ke hasil algoritma. Tugas kita adalah menghubungkan satu set objek tertentu dengan jaringan komunikasi. Perbandingan hasil algoritma terjadi dengan jaringan jalan yang dibangun sebelumnya. Total panjang jaringan yang ada adalah 153,5 km versus 122,6 km untuk yang dihitung. Ini memberikan pengurangan sekitar 25% dalam panjang jaringan jalan, yang pada akhirnya akan menghemat sekitar 5-15% pada biaya konstruksi modal.
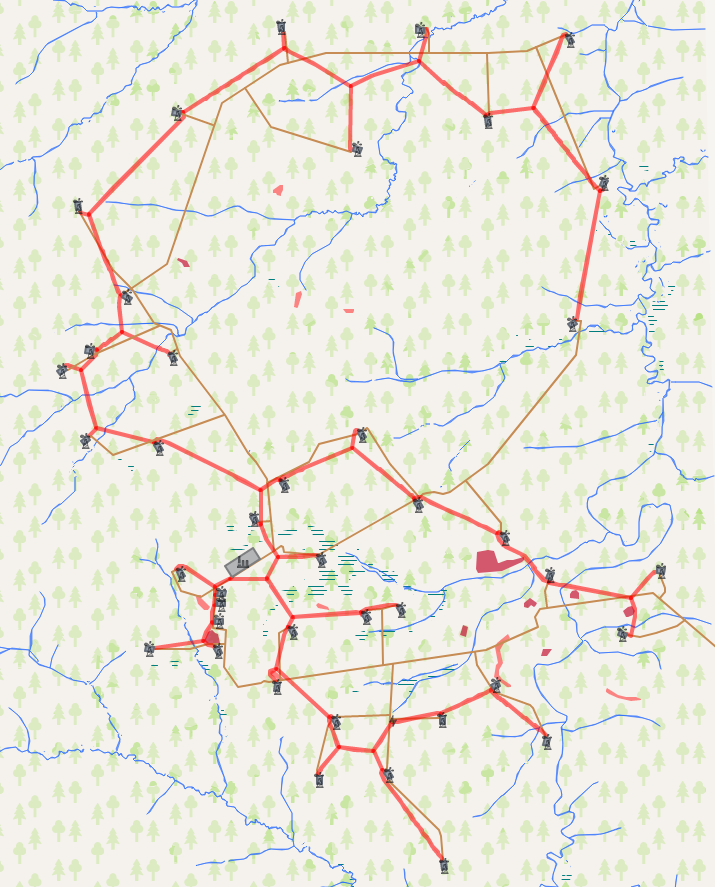
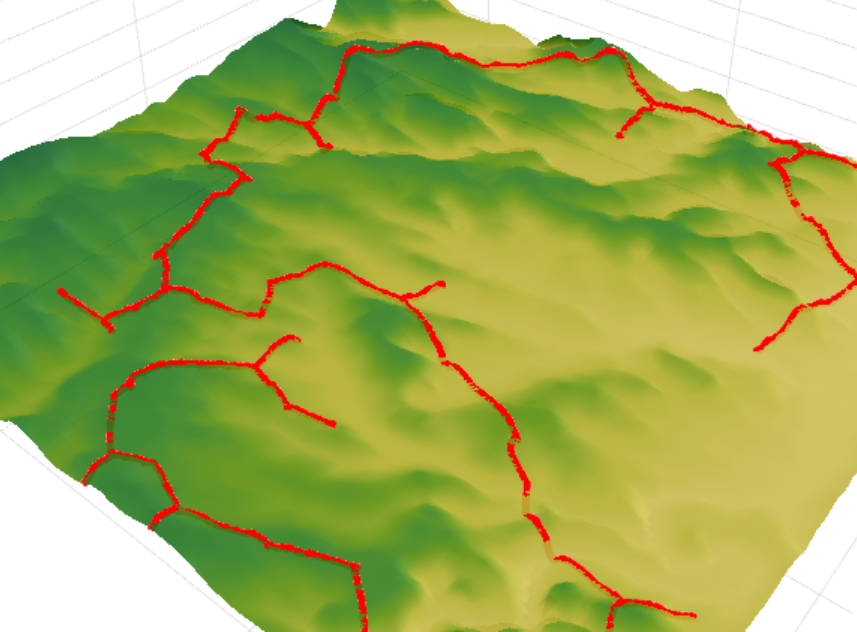
Anda dapat melihat lebih dekat hasil perhitungan di
sini .
Deskripsi metode pengoptimalan yang digunakan akan ada di bagian artikel selanjutnya.