Paku di mana-mana
Kami memanggilnya Spikey, dan dalam hidup saya hari ini saya bertemu dengannya terus-menerus:
Itu berasal dari objek tiga dimensi, sebuah polyhedron yang disebut "rhombic sixtieth."
Tapi apa sejarahnya dan mengapa kita menjadikannya simbol kita?
The Origin of Thorn
Pada tahun 1987, ketika kami mengembangkan versi pertama Mathematica, salah satu inovasinya adalah kemungkinan menghasilkan grafis tiga dimensi resolusi-independen berdasarkan deskripsi simbolis. Dalam demonstrasi awal, ini memungkinkan kami untuk menghasilkan gambar polihedra biasa yang sangat jelas. Tetapi, mendekati rilis Mathematica 1.0, kami ingin menggunakan beberapa contoh yang lebih mengesankan. Oleh karena itu, kami memutuskan untuk mengambil polyhedron reguler terakhir -
icosahedron - dan membuat sesuatu yang lebih rumit darinya dengan memberinya bentuk bintang, atau, lebih tepatnya, akumulasi. Ya, seperti itulah tampilan antarmuka notebook pertama 30 tahun yang lalu.
Pada awalnya itu hanya demonstrasi yang bagus yang bekerja cukup cepat di komputer kita saat itu. Tetapi segera objek tiga dimensi yang dihasilkannya mulai de facto digunakan sebagai logo untuk Mathematica. Dan pada saat versi 1.0 dirilis pada tahun 1988, icosahedron yang terkenal ada di mana-mana:
Seiring waktu, berbagai dedikasi untuk polyhedron bintang kami mulai muncul - dibuat dalam berbagai bahan dan ukuran:
Tetapi, hanya setahun setelah Mathematica 1.0 dirilis, kami siap untuk merilis Mathematica 1.2, dan untuk menyampaikan kompleksitas produk, kami membutuhkan logo yang canggih. Salah satu pengembang kami, Igor Rivin, mempertahankan tesis doktoralnya tentang polyhedra di ruang hiperbolik - dan berkat usahanya, bahan untuk versi 1.2 dihiasi dengan icosahedron hiperbolik:
Karyawan saya memberi saya sebuah T-shirt dengan Shipastik modern untuk ulang tahun saya yang ke-30 pada tahun 1989, dan kutipan yang saya dukung bahkan setelah bertahun-tahun:
“Perusahaan itu menyenangkan”Setelah rilis Mathematica 1.2, dalam materi pemasaran kami, orang dapat menemukan seluruh koleksi polyhedra reguler hiperbolik, tetapi dengan munculnya versi 2.0 pada tahun 1991, kami memutuskan bahwa kami paling menyukai icosahedron hiperbolik:
Tapi kami terus mengeksplorasi bentuk berduri lainnya. Terinspirasi oleh gambar Leonardo da Vinci tentang "model kayu" dari icosahedron bintang (dibuat dengan perspektif yang sangat tepat) untuk buku
Luke Pacioli "Pada Proporsi Ilahi", kami memesan poster versi 2.0 di mana lima tetrahedron berpotongan disusun sedemikian rupa sehingga simpul luarnya membentuk dodecahedron:
Hari ini, melihat arsip saya dari tahun 1991, saya menemukan kode "jelas", dan senang melihat bahwa itu mudah dieksekusi dalam versi terbaru bahasa Wolfram kami (meskipun hari ini dapat ditulis sedikit lebih elegan):
Selama bertahun-tahun, ini telah menjadi ritual aneh - dalam persiapan untuk peluncuran versi utama Mathematica berikutnya, kami akan mengadakan pertemuan serius di mana kami terlibat dalam “memilih Shipastik baru”. Terkadang Anda harus memilih dari ratusan opsi berbeda yang dibuat menggunakan algoritma yang sama sekali berbeda:
Tetapi, meskipun palet warna bermutasi, dan Shipastik sering mencerminkan kehadiran fitur baru dalam sistem (walaupun agak tersirat), kami memiliki tradisi 30 tahun dalam memilih opsi untuk dodecahedron hiperbolik:
Baru-baru ini, sudah menjadi kebiasaan untuk mempelajari ruang parametrik - meskipun sekarang kami telah mengumpulkan ratusan parameter:
Dodecahedron hiperbolik memiliki 20 puncak - itu ideal untuk merayakan peringatan 20 tahun Mathematica pada 2008. Tetapi ketika kami ingin melakukan sesuatu yang serupa untuk peringatan 25 tahun 2013, kami dihadapkan dengan masalah kurangnya polyhedra reguler dengan 25 simpul. Tetapi (pada kenyataannya, menggunakan fungsi
SpherePoints [25]), kami dapat membuat
angka perkiraan , dan mencetaknya pada printer 3D untuk semua karyawan perusahaan, dengan ukuran yang sesuai dengan panjang layanan karyawan.
Keluar dari Wolfram | Alpha
Pada tahun 2009, kami bersiap-siap untuk merilis Wolfram | Alpha, dan sistem membutuhkan logo. Ada banyak konsep:
Kami ingin menekankan bahwa Wolfram | Alpha bekerja dengan perhitungan, dan bukan, katakanlah, sebagai mesin pencari. Dan untuk beberapa waktu kami ingin menggunakan sesuatu dengan roda gigi. Tapi kami juga ingin logo itu menyerupai logo Mathematica yang sudah lama ada. Ini memunculkan salah satu proyek seperti "jenderal kami menjadi gila": penciptaan mekanisme roda gigi dari bentuk berduri.
Seorang pengguna lama Mathematica dan Wolfram Language, seorang insinyur mesin dari Hongaria, Sandor Kabai, membantu kami dengan mengusulkan "gigi berduri":
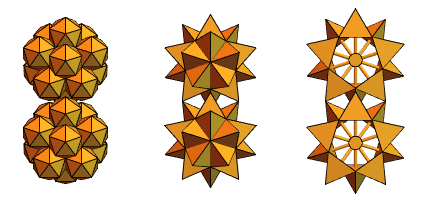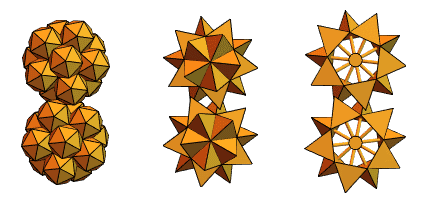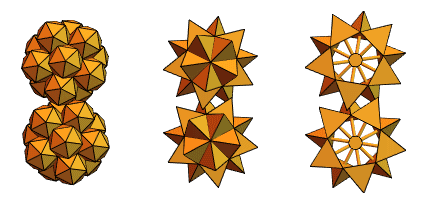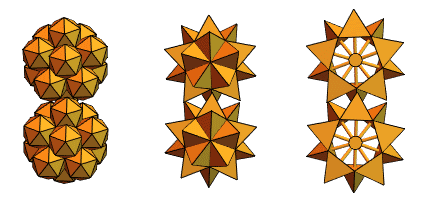
Kembali ke tetrahedron berpotongan dari versi 2, ia menciptakan sesuatu seperti ini:
Pada tahun 2009, printer 3D menjadi sangat populer, dan kami pikir akan menyenangkan untuk membuat logo untuk Wolfram | Alpha yang dapat dicetak. Polyhedron hiperbolik tidak cocok - paku bisa putus dan menimbulkan ancaman. Bentuk seperti paku dari versi ke-4, dengan "paku aman", tidak memiliki keanggunan.
Untuk sementara kami menempel ide dengan roda gigi. Tetapi pada akhirnya, mereka memutuskan bahwa ada baiknya melihat polihedron biasa. Tapi polyhedron mana yang bisa kita pilih?
Tentu saja, ada kemungkinan polyhedra yang tak terbatas. Tetapi untuk logo kami, kami ingin memilih polyhedron yang simetris dan, sampai batas tertentu. Lima polihedra biasa (atau "padatan Platonis") - yang wajahnya adalah poligon reguler yang sama - dapat dianggap sebagai "paling teratur" dari semua:
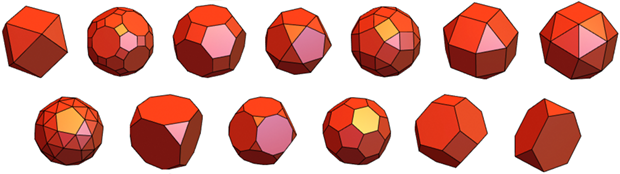
Ada 13 badan Archimedean lebih - mereka memiliki simpul identik, dan poligon reguler, meskipun dari berbagai jenis, bertindak sebagai wajah:
Ada banyak jenis "kebenaran" polyhedra. Salah satu contoh adalah "polyhedra homogen" yang ditunjukkan oleh sebuah
poster dari The Mathematica Journal dari tahun 1993:
Selama bertahun-tahun Eric Weinstein mengumpulkan koleksi itu, yang pada tahun 1999 berubah menjadi MathWorld, ia mencoba memasukkan artikel tentang sebanyak mungkin poligon. Pada tahun 2006, sebagai bagian dari pencantuman berbagai data sistematis dalam Mathematica dan Bahasa Wolfram, kami mulai memasukkan data poligon dengan MathWorld. Akibatnya, setelah rilis versi 6.0 pada 2007, fungsi
PolyhedronData muncul di dalamnya, yang berisi data komprehensif tentang 187 poligon luar biasa:
Dalam Mathematica dan Wolfram Language, Anda selalu bisa menghasilkan poligon reguler, tetapi sekarang sudah lebih mudah dilakukan. Dengan versi 6.0, kami juga merilis Proyek Demonstrasi Wolfram, yang dengan cepat mulai mengisi kembali dengan berbagai demo yang terkait dengan polyhedra.
Salah satunya dibuat oleh putri saya Katerina ketika ia berusia 10 tahun (hari ini ia terus berkembang di bidang geometri): ini adalah "koala polihedral", dirinci oleh semua polihedron dari PolyhedronData [] digunakan:
Terhadap latar belakang seperti itu, pada tahun 2009 kami ingin "memilih polyhedron" untuk Wolfram | Alpha. Semuanya diputuskan pada hari Jumat, 6 Februari, ketika saya mulai bekerja sendiri.
Saya telah menyimpan notebook itu, dan itu menunjukkan bahwa saya pertama kali mencoba menerapkan gagasan yang meragukan menempatkan bola di simpul polyhedra:
Tetapi, seperti yang dicatat dalam
Sejarah Notebook , hanya dua menit kemudian, saya beralih ke polyhedron murni - semuanya berwarna oranye, yang kemudian ingin kami gunakan untuk logo:
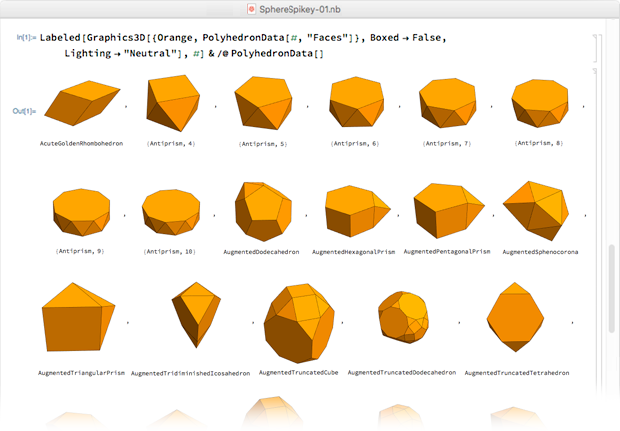
Polyhedra disusun dalam urutan abjad dengan nama, dan pada baris ke-28 ia muncul - hahahedron belah ketupat.
Beberapa menit kemudian, pada pukul 00:24:24, 7 Februari 2009, saya menemukan heksahedron belah ketupat ini dan mengubahnya menjadi posisi simetris, yang kami gunakan sekarang:
Saya ingin melihat bagaimana tampilannya menjadi abu-abu dan siluet, dan empat menit kemudian saya menggunakan
ColorSeparate untuk mencari tahu:
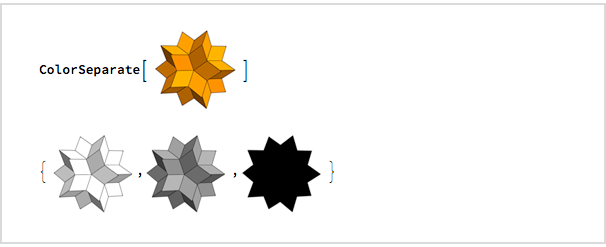
Saya segera mulai menulis email, yang saya kirim pukul 00:32:
Saya sangat suka RhombicHexecontahedron. Ini memiliki bentuk yang menarik dan sangat simetris. Menurut saya keakuratannya cocok untuk kita, dan siluetnya terlihat cukup masuk akal.
Jelas, saya hanya menyalin RhombicHexecontahedron dari notebook (saya ragu bahwa saya bisa menulis hexagon [hexecontahedron] tanpa kesalahan). Dari arsip saya, saya tahu bahwa ini adalah pertama kalinya saya menulis nama polyhedron, yang ditakdirkan untuk menjadi favorit saya.
Dalam Bahasa Wolfram, sangat mudah untuk mendapatkan gambar heksahedron belah ketupat, dan bermain dengannya:
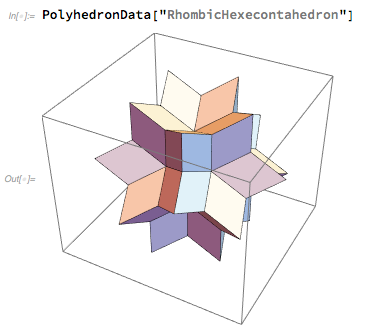
Pada hari Senin, sudah jelas bahwa hexahedron belah ketupat telah menang - dan departemen visual kami sibuk menggambarkannya sebagai logo untuk Wolfram | Alpha. Kami mencoba berbagai orientasi itu, tetapi pada akhirnya kami menentukan posisi simetris “dalam tampilan penuh” yang saya pilih. (Kami juga harus memilih "focal length" terbaik untuk sudut yang paling cocok).
Seperti icosahedron bintang kami dari versi 1.0, hexahedron rhombic memiliki 60 wajah. Tetapi entah bagaimana, berkat kombinasi "lima kelopak", tampilannya jauh lebih elegan. Cukup banyak upaya dihabiskan untuk memilih bayangan wajah sedemikian rupa sehingga gambar dua dimensi dengan benar mencerminkan objek tiga dimensi. Namun segera kami memperkenalkan versi resmi pertama logo kami:
Dia dengan cepat mulai muncul di mana-mana, dan, sebagai penghormatan terhadap ide awal kami, seringkali dengan latar belakang yang dihiasi dengan roda gigi:
Beberapa tahun kemudian, kami sedikit memperbaiki bayangan tepian, yang mengarah pada pembuatan logo Wolfram | Alpha, yang masih digunakan:
Segi enam belah ketupat
Apakah hexahedron rhombic? Dalam bahasa Inggris, ini disebut hexecontahedron, karena memiliki 60 wajah, dan ἑξηκοντα (hexekont) adalah kata Yunani untuk “60”. Wajahnya adalah
belah ketupat emas , yang dinamai demikian karena diagonal mereka berhubungan satu sama lain sesuai dengan rasio emas: φ = (1 + √5) / 2 & sime; 1,618:
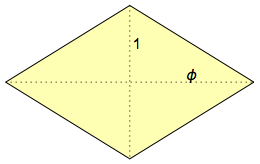
Hexahedron belah ketupat adalah benda antara yang menarik antara icosahedron dan dodecahedron (dengan icosododecahedron di antara mereka). 12 simpul bagian dalam hexahedron belah ketupat membentuk icosahedron biasa, dan 20 simpul luar membentuk dodecahedron biasa. 30 "puncak menengah" membentuk icosododecahedron, dengan facet 32 (memiliki 20 wajah segitiga dan 12 segi lima):
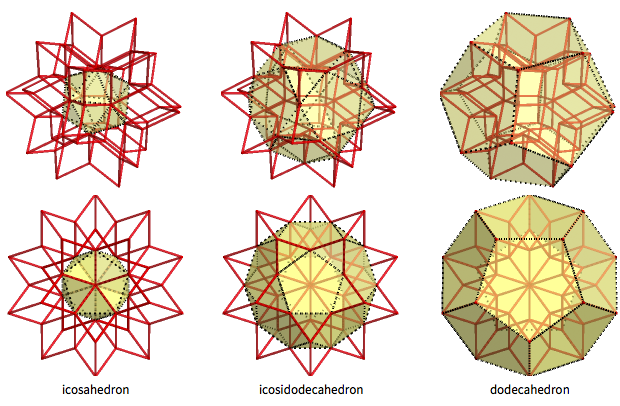
Secara total, hexahedron rhombic memiliki 62 simpul dan 120 tepi (serta 120-62 + 2 = 60 wajah). Ini memiliki tiga jenis simpul ("internal", "tengah" dan "eksternal"), sesuai dengan 12 + 30 + 20 simpul dari icosahedron, icosododecahedron dan dodecahedron. Pada simpul-simpul ini, masing-masing 3, 4, dan 5 sisi saling bertemu. Setiap wajah memiliki satu "internal" titik di mana 5 sisi bertemu, satu titik eksternal di mana tiga sisi bertemu, dan dua "menengah" di mana 4 sisi bertemu. Vertikal luar dan dalam adalah sudut siku-siku dari belah ketupat emas, dan yang menengah adalah sudut tumpul.
Sudut di puncak runcing dari belah ketupat emas adalah 2 tan
−1 (φ
−1 ) ≈ 63.43 °, dan pada puncak runcing tumpul adalah 2 tan
−1 (φ) ≈ 116.57 °. Sudut semacam itu memungkinkan Anda untuk merakit
hahahedron belah ketupat dari konstruktor
Zometool hanya dengan menggunakan penyangga merah (seperti dalam kasus dodecahedron):
Dari 120 tepi heksahedron belah ketupat dari 60 "engsel internal", sudut dihedral adalah 4π / 5 = 144 °, dan untuk 60 yang eksternal adalah 2π / 5 = 72 °. Sudut-sudut yang dikontrak oleh simpul luar dan dalam adalah π / 5 dan 3π / 5.
Untuk menggambar heksahedron belah ketupat, Anda perlu mengetahui koordinat tiga dimensi dari simpulnya. Mereka dengan mudah diperoleh dengan menggunakan fakta bahwa hexahedron belah ketupat adalah invarian terhadap kelompok icosahedron, sehingga Anda dapat mulai dengan satu belah ketupat emas dan cukup menambahkan 60 matriks yang membentuk representasi tiga dimensi dari kelompok icosahedron. Ini, misalnya, memberikan koordinat akhir dari simpul dalam {± φ, ± 1.0}, {± 1, ± φ, ± (1 + φ)}, {± 2φ, 0,0}, {± φ, ± ( 1 + 2φ), 0}, {± (1 + φ), ± (1 + φ), ± (1 + φ)} dan permutasi sikliknya dengan semua tanda yang mungkin.
Selain fakta bahwa wajah heksahedron belah ketupat adalah rhombus emas, heksahedron belah ketupat dapat dibangun dari 20
rhombohedron emas (di mana semua enam wajah adalah rhombus emas):
Ada cara-cara lain untuk membuat hexahedron belah ketupat dari polyhedra lainnya. Ini dapat diperoleh dari lima kubus berpotongan dan dari 182 dodecahedron yang bersentuhan dengan wajah:
Anda tidak dapat membuat mosaik rhombic enam puluh heksahedron terus menerus, tetapi mereka saling menyatu dengan baik (dan, ya, saya melihat lusinan kertas Shipastik melipat dengan cara ini):
Anda juga dapat membuat semua jenis dering dan konfigurasi lainnya:
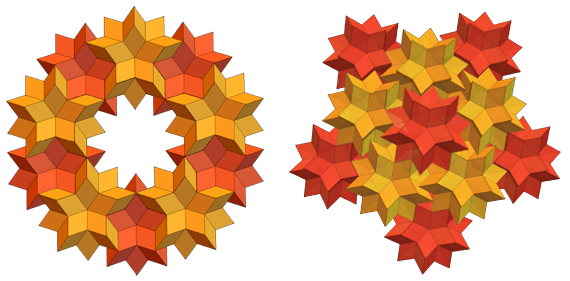
Kerabat dekat hexahedron belah ketupat (RS) adalah tiga puluh tetrahedron belah ketupat (RT). RS dan RT memiliki wajah yang merupakan belah ketupat emas. Tetapi RS memiliki 60 di antaranya, dan RT memiliki 30. Inilah yang terlihat seperti RT yang terpisah:
Beberapa RT benar-benar diinvestasikan dalam kantong RS, dan hal-hal serupa terjadi:
Sandor Kabay, yang disebutkan sebelumnya, menjadi tertarik pada RSh dan RT sekitar tahun 2002. Dan setelah peluncuran Proyek Demonstrasi Wolfram, ia, bersama dengan ahli matematika Slovenia, Isidor Hafner, menambahkan lebih dari seratus demonstrasi ke proyek yang berkaitan dengan RS, RT dan banyak properti mereka:
Model kertas runcing
Segera setelah kami memutuskan bahwa Shipastik akan menjadi RS, kami mulai membuat model 3D-nya. Sekarang sangat mudah untuk melakukan ini menggunakan fungsi Printout3D [PolyhedronData [...]], dan
model yang sudah
dihitung dapat ditemukan pada
sumber daya pihak ketiga .
Pada bulan Mei 2009, ketika Wolfram | Alpha diluncurkan, kami sudah memiliki banyak Paku 3D:
Tetapi, bersiap untuk musim liburan pertama setelah acara ini, kami memutuskan untuk memberikan semua orang kesempatan untuk membuat Shipastik tiga dimensi mereka sendiri. Pertama, kami mempertimbangkan opsi dengan 20 magnet rhombohedral yang dilapisi plastik. Tapi mereka keluar mahal, dan tidak saling menempel dengan baik.
Ini membawa kami pada ide membuat Shipastik dari kertas atau karton tipis. Karena itu, pada awalnya kami ingin membuat diagram yang dapat dimasukkan ke dalam Shipastika:
Anak perempuan saya, Katerina, berperan sebagai penguji (dan ia masih memiliki sampel uji), tetapi menjadi jelas bahwa banyak situasi tidak nyaman muncul dalam proses pelipatan, di mana tidak jelas bagaimana cara berpindah dari satu posisi ke posisi lain. Anda dapat membuat sejumlah besar tata letak (ada 43.380 di antaranya hanya untuk dodecahedron dan icosahedron) - dan kami berpikir bahwa mungkin mungkin untuk memilih sesuatu yang lebih baik dari mereka:
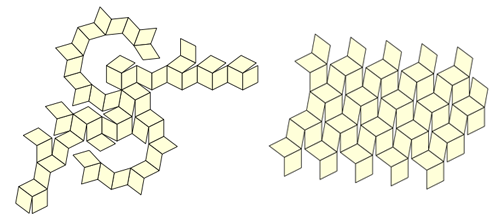
Tetapi, ketika kami tidak dapat menemukan skema seperti itu, kami memiliki ide baru (walaupun jelas): jika model itu akan bertahan di telinga, mengapa tidak membuatnya dari beberapa potong? Kami dengan cepat menyadari bahwa untuk ini, Anda hanya perlu mengambil 12 potong yang identik dari jenis ini:
Dengan bantuan mereka, kami menciptakan "
set untuk patung kertas ":
Tugas yang menarik adalah menulis instruksi yang mudah dimengerti, tetapi setelah beberapa kali pengulangan, instruksi menjadi berkembang dengan baik dan sederhana:
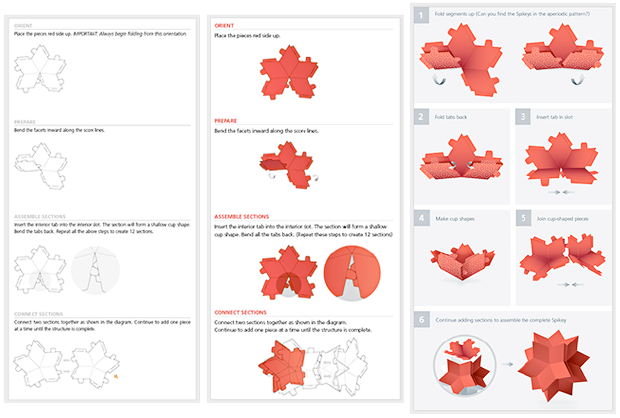
Dan setelah kertas yang dikirimkan Shipastik kepada orang-orang, pengguna kami mulai mengirimi kami semua jenis gambar Shipastik "di darat":
Jalan menuju segi enam belah ketupat
Kubus banyak sisi dari Mesir kunoTidak diketahui siapa yang pertama kali menggambarkan padatan Platonis. Mungkin ini dilakukan oleh
Pythagoras (yang tinggal di dekat endapan besar kristal pirit beraneka segi). Mungkin seseorang melakukan ini jauh sebelum mereka. Mungkin itu sezaman dengan Plato,
Teetet of Athens . Namun, dalam hal apa pun, pada saat Plato (sekitar 400 SM), lima padatan Platonik diketahui. Dan ketika Euclid menulis Elemen-nya (sekitar 300 g SM), salah satu pilar dari karya ini adalah bukti tidak adanya polyhedra biasa lainnya. Bukti ini dikenal untuk mengambil jumlah langkah terbesar dari aksioma Euclidean asli - 32.
Padatan platonis digunakan untuk dadu dan ornamen. Tetapi dia juga ditugaskan peran sentral dalam berpikir tentang alam - misalnya, Plato menyarankan bahwa dalam arti semuanya bisa terdiri dari mereka: bumi dari kubus, udara dari segi delapan, air dari icosahedron, api dari tetrahedron, dan surga ("eter" ) dari dodecahedron.
Bagaimana dengan polyhedron lainnya? Pada abad ke-4 M.
Papp dari Aleksandria menulis bahwa beberapa abad sebelum Archimedes menemukan 13 "polyhedra biasa" lainnya - rupanya, apa yang sekarang disebut badan Archimedean - walaupun rinciannya hilang. Dan selama seribu tahun, sedikit yang terjadi pada polyhedra. Tetapi pada abad ke-15, dengan dimulainya Renaissance, polihedron tiba-tiba menjadi modis kembali. Leonardo da Vinci dan Albrecht Durer secara teratur menggunakannya dalam seni dan desain, menemukan kembali beberapa tubuh Archimedean - serta menemukan polyhedra baru, misalnya, icodosodecahedron.
Tetapi langkah maju terbesar untuk polyhedra adalah
karya Johannes Kepler pada awal abad XVII. Semuanya dimulai dengan teori yang elegan, meskipun sepenuhnya salah. Kepler, berdasarkan asumsi teologis, percaya bahwa Semesta harus dibuat dengan ketepatan matematis, dan menyarankan bahwa keenam planet yang diketahui pada waktu itu bergerak di sepanjang bulatan bersarang yang tertulis dan dijelaskan di sekitar lima benda padat Platonis:
Dalam 1619 bukunya Harmonices mundi, Harmony of the World, Kepler berpendapat bahwa banyak fitur musik, planet, dan jiwa bekerja sesuai dengan hubungan dan prinsip geometris yang sama. Untuk mengkonfirmasi argumen, Kepler mempelajari poligon dan polyhedra, terutama yang tertarik pada objek yang membentuk set lengkap, seperti padatan Platonis.
Dia mempelajari "polyhedra kontak" yang digunakan untuk membuka pesawat - dan menemukan, misalnya, "
ubin mengerikan ", sebagaimana ia menyebutnya (terdiri dari pentagon, pentagram, dan decagon). Dia mempelajari "polyhedron stellate" dan menemukan berbagai versi bintang padatan Platonis (dan
tubuh Kepler - Poinsot ). Pada tahun 1611, ia menerbitkan sebuah buku kecil mengenai struktur kepingan salju heksagonal, yang ditulis sebagai hadiah untuk tahun baru kepada salah satu pelanggannya. Dalam buku ini, ia membahas kemasan tiga dimensi bola (dan atom bola), mengusulkan
hipotesis bahwa kemasan bola terpadat dalam ruang tiga dimensi (kami secara teratur mengamati implementasinya dalam kemasan buah di toko-toko) adalah kemasan kubik berpusat pada wajah (hipotesis ini secara formal terbukti hanya setelah tahun 2000 tahun - menggunakan Mathematica).
Dalam berbagai paket Kepler, berbagai polihedron disembunyikan. Mari kita mulai dari bidang apa pun, bawa tetangga-tetangganya dan hubungkan pusat-pusat mereka untuk membuat simpul-simpul polyhedron. Dalam pengemasan ketat Kepler, 12 lainnya menyentuh bola apa pun, dan dari pusatnya sebuah cuboctahedron dengan 12 simpul dan 14 wajah diperoleh. Tapi Kepler juga menggambarkan paket lain, 8% lebih sedikit padat, di mana masing-masing lingkup ditutupi oleh 8 lainnya, dan 6 lainnya sangat dekat. Jika kita menghubungkan pusat mereka, kita mendapatkan dodecahedron belah ketupat, dengan 14 simpul dan 12 wajah:
Setelah menemukan ini, Kepler mulai mencari "rhombic polyhedra" lainnya. Dalam dodecahedron belah ketupat yang ia temukan, belah ketupat terdiri dari pasangan segitiga sama sisi. Tetapi pada tahun 1619 Kepler juga mempelajari belah ketupat emas - dan menemukan belah ketupat belah ketiganya, setelah itu ia melukis dalam bukunya gambar indahnya, di samping dodecahedron belah ketupat:
Kepler segera menemukan aplikasi untuk poligon belah ketupat: dia ingin menggunakannya dan sebuah kubus untuk membangun model bola bersarang yang cocok untuk orbit empat bulan Jupiter, ditemukan oleh Galileo pada tahun 1610.
Mengapa Kepler tidak membuka hexahedron belah ketupat? Saya pikir dia datang cukup dekat dengannya. Dia mempelajari polihedron bintang non-cembung. Dia melihat polyhedra belah ketupat. Tetapi, tampaknya, untuk teori astronomisnya, tiga puluh sisi belah ketupat sudah cukup, setelah itu ia berhenti mencari.
Akibatnya, tentu saja, hukum Kepler, tidak terkait dengan polyhedron, menjadi kontribusi utama bagi astronomi yang selamat. Tetapi pekerjaan Kepler pada polyhedron - meskipun dilakukan dalam kerangka teori fisik yang salah - tetap merupakan kontribusi abadi untuk matematika.
Selama tiga abad berikutnya, lebih banyak polihedron dari berbagai kebenaran ditemukan - dan pada awal XX matematikawan sudah tahu banyak dari tipenya:
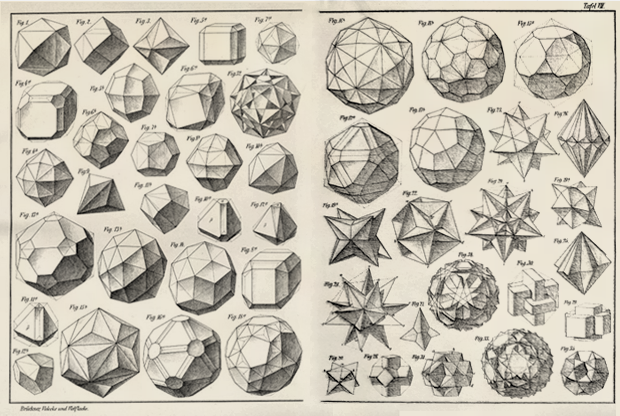
Tapi, sejauh yang saya tahu, tidak ada RS di antara mereka. Penemuannya menunggu karya
Helmut Unkelbach . Lahir pada tahun 1910, ia mempertahankan gelar doktor dalam bidang matematika di Universitas Munich pada tahun 1937 (meskipun ia pertama kali belajar fisika). Dia menulis beberapa karya tentang pemetaan konformal, dan - mungkin karena studi tentang pemetaan polyhedra - pada tahun 1940 menerbitkan karya "Edge-Symmetric Polyhedra" dalam bahasa Jerman.
Dia menjelaskan bahwa tujuannya adalah studi komprehensif dari semua kemungkinan polihedra yang memenuhi definisi baru yang benar tentang kebenaran: semua sisi memiliki panjang yang sama dan berada dalam bidang simetri polihedron. Hasil utama dari karya ini adalah sebuah tabel dengan 20 polyhedra berbeda dari properti ini:
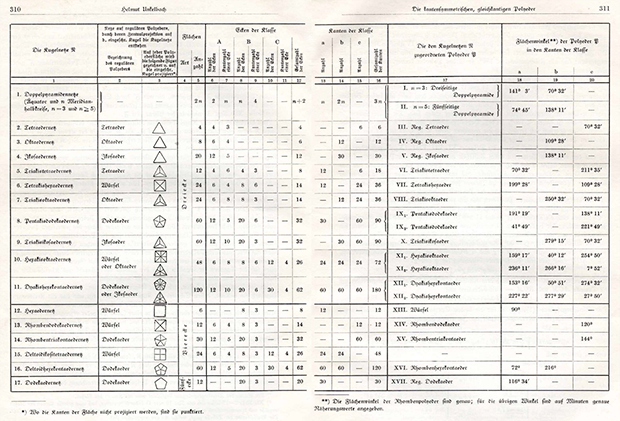DiklikKebanyakan dari mereka sudah terkenal. Tetapi Unkelbach memilih tiga dari mereka yang dianggapnya baru: dua
hexaciscosahedra (atau disdakis dodecahedron), dua
hexacisicosahedra (atau disdacystriacontahedron) dan apa yang disebutnya Rhombenhexekontaeder, atau hexahedron rombomb. Dan dia jelas menganggap RSh pencapaian utama, dan termasuk foto modelnya yang dibuat oleh dirinya sendiri:
Bagaimana dia membawa RS? Dia mulai dengan dodecahedron, dan mendefinisikan dua bidang simetri:
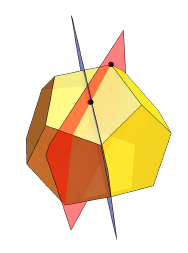
Kemudian dibagi masing-masing wajahnya:
Kemudian, pada intinya, dia memeras bagian tengah dari masing-masing wajah dengan jarak yang sama dengan jarak yang biasa ke pusat dikalikan dengan α tertentu:
Untuk α <1, wajah yang dihasilkan tidak berpotongan. Tetapi untuk sebagian besar nilai α, sisi-sisinya tidak sama. Ini hanya terjadi dalam kasus tertentu - ketika polihedron yang dihasilkan tepat bertepatan dengan RS.
Unkelbach menganggap karyanya pada tahun 1940 sebagai "pemanasan" untuk studi yang lebih luas tentang "k-symmetric polyhedra" dengan persyaratan simetri yang kurang ketat. Tetapi tentu saja sudah merupakan keajaiban bahwa setelah dimulainya
Perang Dunia II , sebuah jurnal matematika diterbitkan di Jerman - tidak lama setelah publikasi ini, Unkelbach dipanggil ke depan, di mana ia mengembangkan torpedo akustik untuk armada Jerman selama beberapa tahun.
Dia tidak menerbitkan lebih banyak karya tentang polyhedra, dan meninggal pada tahun 1968. Setelah bertahun-tahun, dia kembali ke pemetaan konformal, dan juga mulai menerbitkan
teori pemilihan , menganggapnya sebagai kunci untuk menciptakan demokrasi yang berfungsi dengan baik, dan berpikir bahwa matematikawan berkewajiban membuat orang mulai menggunakannya.
Tetapi, bahkan muncul dalam sebuah karya tahun 1940, RS dapat tinggal di sana selamanya jika pada tahun 1946 seseorang
Harold Scott MacDonald Coxeter tidak menulis ulasan singkat tentang karya ini untuk jurnal yang relatif baru, American Mathematical Reviews. Ulasannya mencantumkan polyhedron yang disebutkan dalam penelitian ini, karena seorang naturalis dapat membuat daftar spesies baru yang ditemukan olehnya dalam ekspedisi. Hal utama adalah bahwa ia menggambarkan di sana "hexahedron rhombic yang luar biasa", dan menyebutkan bahwa "bentuk wajahnya bertepatan dengan bentuk wajah sisi tiga puluh, dari mana diperoleh dengan memberikan bentuk bintang".
Polyhedron bukan topik populer dalam matematika pada pertengahan abad ke-20, tetapi Coxeter adalah pendukung utama mereka - dan entah bagaimana terhubung dengan semua orang yang mempelajarinya. Pada 1948, ia menerbitkan buku The Right Political Scientists. Ini secara sistematis menggambarkan berbagai keluarga polihedra biasa, khususnya, dan polihedron bersisi
tiga puluh bintang yang besar - pada kenyataannya, mengandung RS:
Namun dalam bukunya, Coxeter tidak secara eksplisit menyebutkan RS, dan meskipun ia merasa terhormat dengan referensi dari beberapa pecinta polyhedron, RS terus sedikit diketahui.
Kristal kuasi
Kristal selalu menjadi contoh penting polihedra di alam. Tetapi pada abad ke-19, ketika teori atom memperoleh pengakuan yang semakin banyak, para ilmuwan mulai melakukan penelitian yang lebih dan lebih serius di bidang kristalografi dan pengaturan atom dalam kristal. Polyhedra mulai sering muncul, khususnya, dalam representasi geometri blok berulang atom ("sel") dalam kristal.
Pada 1850, diketahui bahwa hanya ada 14 geometri seperti itu - di antara mereka ada juga yang didasarkan pada dodecahedron belah ketupat. Mereka penting untuk kehadiran simetri urutan kedua, ketiga, keempat atau keenam - yang, pada dasarnya, adalah konsekuensi dari kenyataan bahwa ruang hanya dapat diisi dengan polyhedra tertentu, sama seperti hanya poligon biasa seperti kotak dapat mengisi bidang dua dimensi, segitiga dan segi enam.
Bagaimana dengan bahan non-kristal lainnya - seperti cairan atau gelas? Sejak awal abad ke-20, orang-orang telah tertarik pada kemungkinan kehadiran setidaknya simetri urutan kelima di sana. Tidak mungkin untuk mengisi ruang dengan icosahedron yang benar, tetapi dimungkinkan untuk membuat bagian ruang dua sisi dengan celah kecil di antaranya.
Pertanyaan ini tetap tidak terselesaikan sampai tahun 1980-an, ketika kristalografi difraksi elektron menggunakan paduan aluminium dan mangan yang didinginkan dengan cepat menunjukkan adanya simetri berlipat lima. Teori-teori untuk mencapai simetri seperti itu sudah ada, dan setelah beberapa tahun, gambar-gambar yang dibuat oleh mikroskop elektron juga muncul, di mana partikel-partikel yang memiliki bentuk belah ketupat belah ketupat terlihat:
Dan, sementara orang-orang membayangkan bagaimana tiga puluh heptahedron ini dapat digabungkan satu sama lain, sebuah sixta-hexa belah ketupat muncul - dalam bentuk "lubang" dalam kelompok 12 trihedra rhombik:
Pada awalnya itu disebut bintang berujung 20. Tapi kemudian dikaitkan dengan deskripsi dalam literatur pada polyhedron, dan diidentifikasi sebagai RS.
Sementara itu, gagasan untuk membuat objek dari elemen belah ketupat semakin populer. Michael Longe Higgins, seorang ahli kelautan dan ahli dalam pembentukan gelombang laut, bergabung dengan hobi massa, dan pada tahun 1987 ia mematenkan mainan berdasarkan elemen rhombohedral, dari mana dimungkinkan untuk merakit "bintang Kepler" (RS) atau "bola Kepler" (tiga puluh belah ketupat) ):
Dan - walaupun saya baru mengetahuinya sekarang - blok rhombohedral, yang kami pertimbangkan pada tahun 2009 sebagai pilihan untuk membuat "Shipastiks," sebenarnya diproduksi oleh perusahaan Dextro Mathematical Toys (Rhombo.com), yang bekerja di pangkalan Longge-Higgins di San Diego
Masalah berhasil mengisi ruang dengan angka tiga dimensi - atau bahkan pesawat dengan angka dua dimensi - agak rumit. Telah diketahui sejak tahun 1960-an bahwa dalam kasus umum, masalah apakah satu set formulir tertentu dapat mengisi pesawat tidak dapat dipecahkan. (Pada prinsipnya, dapat diperiksa apakah 1000 formulir ini dapat dikomposisikan satu sama lain, tetapi semakin banyak formulir yang kami pertimbangkan, semakin banyak sumber daya komputasi yang diperlukan).
Orang-orang seperti Kepler mungkin berasumsi bahwa jika satu set bentuk dapat mengisi bidang, maka ini dapat dilakukan sebagai pola berulang. Namun, setelah menjadi jelas bahwa dalam kasus umum masalah ini tidak diselesaikan,
Roger Penrose pada tahun 1974 muncul dengan dua bentuk yang dapat mengisi pesawat tanpa mengulangi pola. Pada tahun 1976, Penrose (dan Robert Ammann) muncul dengan versi sederhana dari bentuk-bentuk ini:
Dan, ya, bentuk-bentuk ini terlihat seperti belah ketupat, meskipun bukan emas. Tetapi dengan sudut 36 °, 144 ° dan 72 °, 108 °, mereka memiliki simetri 5 kali lipat dan 10 kali lipat.
Rhombus ini tidak bisa mengeluarkan pola berulang. Tetapi ternyata mereka dapat menyusun pola yang dibangun secara sistematis:
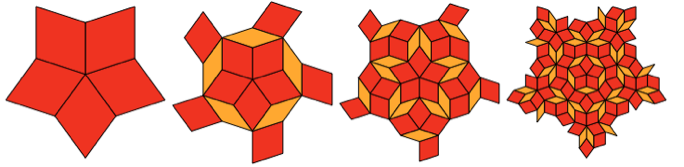
Dan, ya, bagian tengah dari langkah ke-3 sangat mirip dengan Shipastik yang rata. Tapi itu tidak sepenuhnya bertepatan dengan itu, belah ketupat eksternal memiliki format yang sedikit berbeda.
Namun, hubungan dekat di antara mereka masih ada. Bayangkan bahwa kita akan mulai bukan dari pesawat, tetapi dari setengah dari tiga dimensi belah ketupat tiga dimensi persegi, yang terdiri dari belah ketupat emas:
Dari atas, terlihat persis seperti awal desain mosaik Penrose bersarang. Jika kami melanjutkan proses ini, kami mendapatkan mosaik ini:
Jika Anda melihatnya "dari samping", Anda dapat melihat bahwa ini masih merupakan rhombus emas yang sama:
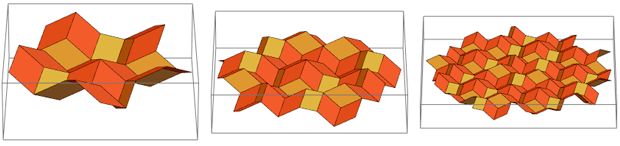
Setelah mengompilasi empat "atap Wieringa" ini, Anda hanya bisa mendapatkan RS:
Apa hubungan antara struktur tertanam ini dan cara nyata pembentukan quasicrystals fisik? Belum jelas. Tapi itu cukup menarik untuk melihat bagaimana petunjuk RS muncul di alam.
Secara historis, itu berkat diskusi tentang quasicrystals bahwa Sandor Kabaei mulai belajar RS menggunakan Mathematica, yang membuat Eric Weinstein menemukan mereka, yang menyebabkan mereka dimasukkan ke dalam Mathematica dan Wolfram Language, yang membuat saya memilih salah satu dari mereka untuk logo kami. Untuk menghormati ini, kami mencetak mosaik Penrose di dalam Paper Shipastik kami:
Meratakan Duri
Shipastik kami untuk Wolfram | Alpha meledak ke dunia pada tahun 2009 dengan merilis Wolfram | Alpha. Tetapi kami juga memiliki Shipastik kami untuk Mathematica, yang telah berkembang dan berkembang untuk waktu yang lama. Karena itu, ketika kami membangun kantor pusat Eropa kami yang baru di tahun 2011, dua Shipastik berkompetisi untuk hadir di dalamnya.
Direktur seni lama kami Jeremy Davis datang dengan yang berikut: ambil salah satu Shipastiks dan "jadikan ideal" dia hanya menggunakan "kerangka" -nya. Keputusan untuk memulai dengan RS adalah keputusan yang sederhana. Tapi kemudian kami meratakannya, dan versi pertama dari logo yang sekarang dikenal muncul:
Kejutan Brasil
Ketika saya memulai artikel ini, saya pikir keseluruhan cerita akan berakhir di sana. Lagipula, saya telah menjelaskan bagaimana kami memilih RS untuk diri kami sendiri, dan bagaimana ahli matematika datang dengan itu. Tetapi sebelum saya selesai menulis, saya memutuskan: "Saya akan memeriksa semua surat tentang Shipastik selama bertahun-tahun, hanya untuk memastikan bahwa saya tidak melewatkan apa pun."
Dan kemudian saya melihat email dari Juni 2009 dari artis Brasil Yolanda Kipriano. Dia menulis bahwa dia melihat artikel tentang Wolfram | Alpha di majalah berita Brasil, menarik perhatian ke Shipastika, dan memberikan tautan ke situsnya. Lebih dari 9 tahun telah berlalu sejak itu, tetapi saya masih mengikuti tautan ini, dan kagum melihat yang berikut:
Saya terus membaca suratnya: "Di Brasil, objek ini disebut Giramundos atau" bunga Mandakaru "dan terbuat dari serbet sebagai ornamen artistik."
Apa? Di Brasil ada tradisi yang terkait dengan Shipastik, dan selama bertahun-tahun kita belum pernah mendengarnya? Segera saya menemukan gambarnya di internet. Sebagian kecil model terbuat dari kertas, sebagian besar terbuat dari kain - tetapi ada banyak dari mereka:
Saya menulis kepada teman saya dari Brazil yang mengerjakan versi pertama Wolfram | Alpha. Dia dengan cepat menjawab: "Benda-benda ini benar-benar tampak akrab. Sayangnya, saya tidak punya keinginan yang cukup untuk membandingkan dua dan dua, "dan mengirimi saya foto-foto dari katalog lokal karya seni dan kerajinan:
Perburuan dimulai: apa benda-benda ini dan dari mana asalnya? Seseorang dari perusahaan kami mengatakan bahwa nenek buyutnya dari Chili merajut hal-hal seperti itu, dan selalu membuat mereka membuntuti. Kami mulai berhubungan dengan orang-orang yang memposting gambar "folk shipastiks" di internet. Cukup sering ternyata mereka membeli salinan mereka di toko. Tetapi kadang-kadang orang mengatakan bahwa mereka tahu cara membuatnya. Dan setiap orang memiliki kisah yang hampir sama: mereka belajar ini dari nenek mereka.
Cara khas untuk mengumpulkan paku rakyat - setidaknya di zaman kita - adalah memotong 60 berlian dari kardus. Maka semua orang perlu dibungkus kain, dan menjahitnya bersama:
Namun kemudian masalah matematika segera muncul. Apakah orang-orang ini menandai dengan benar dan mengukir belah ketupat emas dengan sudut 63 °? Biasanya tidak. Mereka membuat belah ketupat dengan 60 ° dari pasangan segitiga sama sisi - ini adalah bentuk belah ketupat standar yang digunakan dalam pembuatan selimut. Jadi bagaimana Thornies terjadi? Nah, perbedaan antara 60 ° dan 63 ° kecil, dan jika Anda menjahit wajah bersama-sama, maka akan ada cukup ruang di antara mereka untuk bermanuver, jadi cukup sederhana untuk membuat polyhedron tanpa mencapai sudut yang benar-benar akurat. (Ada juga quasi-Shipastiks, di mana, seperti dalam pembangunan Unkelbach, bukannya wajah tidak ada belah ketupat, tetapi "segitiga eksternal" yang tajam).
Paku di Internet ditetapkan secara berbeda. Paling sering - Giramundos. Seringkali mereka disebut Estrelas da Felicidade ("bintang kebahagiaan"). Fakta bahwa mereka kadang-kadang disebut "bintang-bintang Moravian" membingungkan, tetapi pada kenyataannya,
bintang -
bintang Moravia adalah polihedron yang jauh lebih tajam (paling sering terbuat dari rhombocubooctahedron), yang baru-baru ini mendapatkan popularitas sebagai luminer.
Meskipun penyelidikan panjang, saya masih tidak tahu seluruh sejarah paku rakyat. Inilah yang saya temukan. -, ( ). -, , XX , , , . , , , .
, , , ---. , , , - « 50».
( «») , , , , . – , – , ( - ), , 15 .
? . , , , 1900 . , 80- , , 200- , , , .
, , , . , . , – - , , .
Namun, twist lain ditemukan dengan paku rakyat: sering sebelum menjahit mainan, sang ibu memasukkan uang yang bisa digunakan putrinya dalam kasus-kasus kritis. Dan putrinya menyimpan shipastiknya bersama dengan perlengkapan menjahitnya, di mana suaminya tidak akan menemukannya. Beberapa paku digunakan sebagai peniti bantal - yang mungkin menjadi penghambat tambahan bagi suami.Keluarga mana yang mendukung tradisi membuat paku rakyat? Sejak sekitar 1750, ada banyak perkebunan kopi dan gula di daerah pedesaan Brasil, jauh dari kota. Sampai sekitar abad ke-20, petani sering membawa gadis-gadis ke pengantin mereka - sering sangat muda, hingga 13 tahun - dari kota-kota terpencil. Mungkin pengantin perempuan ini - biasanya berasal dari keluarga baik keturunan Portugis, dengan pendidikan yang relatif baik - membawa duri rakyat., , . - XX – , , , – . 1950- .
. ( ) , « . » ( – ) - (.. «»), .
Di bagian lain Brasil, mainan sering disebut nama bunga dan buah yang sedikit mirip dengannya. Di timur laut - Flor Mandacarú (dengan nama bunga kaktus). Di lahan basah tropis - Carambola (untuk menghormati buah-buahan carambola, kadang-kadang disebut "bintang tropis"). Di daerah berhutan tengah - Pindaíva (untuk menghormati buah runcing merah).
Tetapi lebih sering daripada tidak, shipastika populer disebut Giramundo, kata Portugis yang agak lama yang secara harfiah berarti "dunia yang berputar-putar". Rupanya, mainan itu digunakan sebagai jimat yang membawa keberuntungan dengan rotasi angin. Ekor mulai melekat pada mereka baru-baru ini, tetapi, tampaknya, itu adalah kebiasaan untuk menggantung mereka di rumah, mungkin pada hari libur., , , , .
( — « ») --- – , , , .
, . , 1963 , - , . , , 1997 :
Jadi dari mana paku rakyat itu berasal? Saya masih belum tahu ini. Mereka dapat muncul di Brasil, mereka dapat berasal dari Portugal atau bagian lain dari Eropa. Fakta bahwa mereka menggunakan potongan-potongan kain dan menjahit untuk pembuatan mereka mungkin merupakan argumen yang mendukung asal mereka dari Afrika atau penduduk asli Amerika., , , – , XIX – ( , , ). , , - , , . , ( ).
, . .
, . (
) – , , , XIII .
– , , , .
, . – :
Wolfram|Alpha . – , , π :
blog.stephenwolfram.com/data/uploads/2018/12/spikey-lives-happy-pi-day-video.mp4Polihedra bersifat abadi. Mereka dapat dilihat pada gambar 500 tahun yang lalu, yang terlihat sejernih dan se modern polyhedron di komputer saya.Saya menghabiskan cukup banyak waktu untuk mencari hal-hal komputasi abstrak (misalnya, automata seluler). Mereka juga memiliki keabadian. Tetapi bagi mereka saya tidak menemukan bukti sejarah. Seperti objek abstrak, mereka dapat dibuat kapan saja. Tetapi mereka muncul hari ini berkat platform dan alat konseptual kami - dan tidak ada yang pernah melihatnya sebelumnya.. . – , .
– , , , . – , , , .
? , , , . , , . .