Peradaban Musim Semi, 1/5

### Bagian 1. Emas "Ku"

Sekitar enam tahun saya jatuh ke tangan pemandu kakek ^[50] di truk-truk pada pertengahan abad ke-20. Padat, dicetak pada buku langka kertas tebal yang halus. Satu-satunya hal yang tersisa dalam ingatan kakek saya setelah runtuhnya negara, perang dan perjalanan.



Buku referensi berisi banyak karakteristik kinerja yang menarik, sehingga kata "kapasitas muat" menjadi akrab bagi saya sejak usia dini. Dan ketika ayah saya berjalan-jalan menyebutkan bahwa truk apa pun memiliki bobot sebanyak yang dibutuhkan, saya ingat itu. Dia ingat dan, lama kemudian, menjadi tertarik.

Ayah benar. Untuk truk tahun 60-an, aturan ini diterapkan dengan akurasi yang agak mengejutkan:



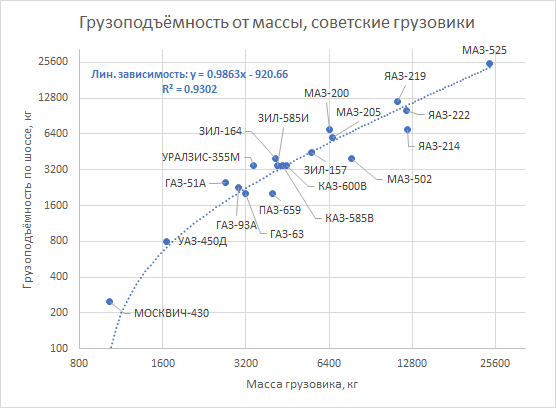
Jauh lebih aneh bahwa pola ini juga diamati untuk kendaraan yang sama sekali tidak seperti truk.

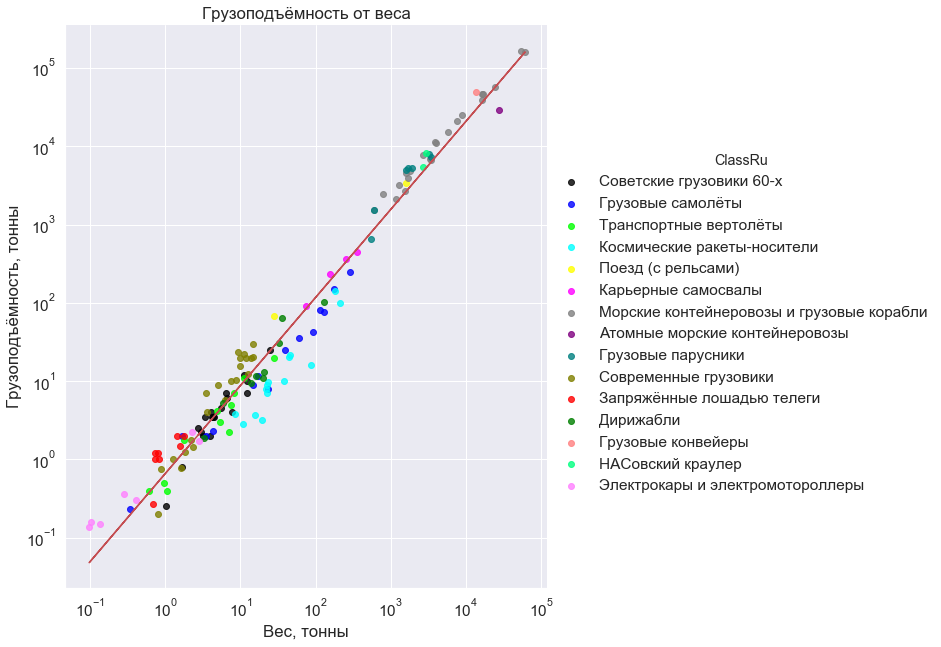
Pada awalnya, untuk bersenang-senang, saya memasukkan pesawat kargo sesuai jadwal. Dan terkejut. Saya mulai menambahkan kendaraan lain. Berkuda, mengambang, dan terbang, dibangun pada abad ke-19, 20, dan 21, bekerja pada energi termal, atom, angin, dan bahkan kuda. Hasil? Daya lemah (indikator 1.125), jika bukan hanya linear, ketergantungan. Pada massa dari ratusan kilogram menjadi enam puluh ribu ton. Dengan penyimpangan, tentu saja, di mana orang bisa pergi tanpa mereka, hingga 10 kali kadang-kadang, tetapi pada enam ordo massa ini jelas merupakan hal yang sepele.

Ini dia, ketergantungan ini, meremas ke diagonal bidang kosong yang luas:


Pada grafik dicatat: pesawat kargo; helikopter pengangkut; kapal udara, abad modern dan awal; kendaraan peluncuran ruang angkasa (dalam orbit rendah); Truk Soviet tahun 60-an; truk pertambangan modern; truk modern Rusia, AS, Cina, dan India; mobil listrik dan skuter; kereta api (dengan rel); kapal kontainer nuklir; kapal kontainer dan kapal kargo (bukan tanker); kapal kargo berlayar 17-20 abad; ban berjalan untuk transfer bijih; Traktor Nassovsky untuk mengekspor rudal ke awal; dan akhirnya gerobak yang ditarik kuda.

Jika Anda memasukkan nilai Q , yang didefinisikan sebagai massa kargo yang diangkut terkait dengan massa kering kendaraan, maka inilah yang terlihat untuk masing-masing kelompok:



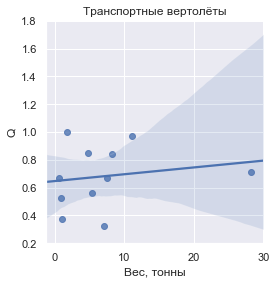
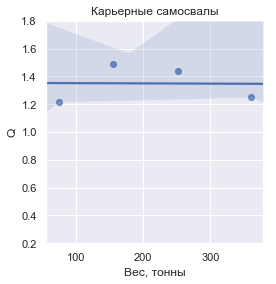
Dalam angka, nilai Q adalah:

Kelas aset	Q rata-rata	Simpangan baku Q
Pesawat kargo	0,667091	± 0,206162
Helikopter Transportasi	0,681605	± 0,225062
Kapal udara, abad modern dan awal	0.842673	± 0,374622
Kendaraan peluncuran luar angkasa (orbit rendah)	0,372446	± 0,155810
Truk Soviet tahun 60-an	0,777435	± 0,232425
Truk penambangan modern	1.349610	± 0,136840
Truk modern Rusia, AS, India, Cina	1.293679	± 0,604313
Kartu dan skuter listrik	1.098433	± 0,343791
Kereta api (dengan rel)	2.275989	± 0,205999
Kapal Kontainer Nuklir	1.035233	± NA
Kapal kontainer laut dan kapal barang (bukan kapal tanker)	2.556004	± 0,378040
Kapal kargo berlayar 17-20 abad	2.488461	± 0,671785
Sabuk pengangkut barang	3.703704	± NA
Traktor Nasovsky untuk peluncuran rudal	2.355919	± 0,525174
Gerobak yang ditarik kuda	1.203061	± 0,389183

Seperti yang dapat dilihat, Q, meskipun tidak di mana-mana benar-benar tunggal, tetapi dalam setiap kelompok cenderung memiliki nilai bersama yang dekat dengan persatuan.


Bagiku ... misterius. Mengapa perahu layar kayu, mobil listrik aluminium, dan kapal kontainer atom yang menampung seratus ribu mobil listrik semuanya menaikkan beratnya kurang lebih? Apa yang membuat kami membuat kendaraan dengan kualitas Q ≈ 1 pada massa yang berbeda ribuan kali? Apakah ini merupakan manifestasi dari sifat-sifat fisika dunia, ekonomi terestrial, apakah ini merupakan keterbatasan kecerdasan manusia? Seberapa universal hukum ini, apakah akan diterapkan untuk peradaban dari bintang lain? Masalah global. Mereka tidak mungkin diselesaikan di sini dan sekarang. Tetapi di sini adalah mungkin dan perlu untuk mempertimbangkan dan menggigit berapa banyak hasilnya. Ini yang akan kita lakukan.

Rekor dunia ^{[ 180 ]} mengangkat barbel oleh orang dengan berat rata-rata melebihi 200 kg. Secara teoritis, ini berarti bahwa tubuh kita memiliki batas keselamatan untuk beban brengsek setidaknya hingga Q = 2,5. Namun, ini membutuhkan kekuatan dan pelatihan yang terlalu tinggi sehingga tidak pernah digunakan dalam kegiatan sehari-hari. Lebih disarankan untuk mengemas gula dalam kantong 50 kilogram, meskipun ini membutuhkan empat kali lebih banyak pemuat atau alat bantu jalan. Perhatikan bahwa situasi ini adalah hasil dari evolusi biologis, di mana kecerdasan manusia tidak (hampir) mengambil bagian, dan karenanya memiliki "alibi" di dalamnya.

Fisika dan teknik saja tidak melarang Qs tinggi. Ada pompa turbo hidrogen untuk mesin mid-flight Shuttle, hal kecil di sebelah kanan dalam gambar yang mengembangkan daya 54 megawatt ^{[ 60 ]} dengan berat total kendaraan 350 kg:

[Kredit gambar: [ 10 ]]

Jika, menyederhanakan, mengevaluasi Q dengan daya per kilogram massa, maka ini 100 kali lebih tinggi daripada mobil yang layak. Tapi benda ini hampir seperti roket! Lebih murah membuat 100 mobil dengan Q = 1 dan mengangkut kargo bersamanya, daripada mencoba "memanfaatkan" unit ini ke troli beroda.

Pertimbangan semacam itu menunjukkan bahwa alasannya di sini bersifat ekonomis. Selain itu, tidak dalam arti sempit ekonomi dan negara tertentu (karena perangkat kami dihasilkan oleh orang-orang dan sistem yang sangat berbeda), tetapi lebih dalam arti "kemanfaatan upaya." Kesesuaiannya cukup universal untuk, tampaknya, berlaku untuk produk yang sangat berbeda dan di suatu tempat bahkan untuk hewan.

_{Artikel ini ditulis untuk situs https://habr.com . Saat menyalin, silakan merujuk ke sumbernya. Penulis artikel ini adalah Evgeny Bobukh .}

Mari kita coba selidiki batas-batas kemanfaatan ini secara kuantitatif. Kami mengajukan pertanyaan: bagaimana biaya perangkat massa tetap tergantung pada Q ? Di sini, misalnya, ada dump truck seberat 10 ton, butuh 10 ton kargo. Kami juga ingin membuat 10-ton, tetapi mengambil 20 ton ( Q = 2) atau bahkan 50 ( Q = 5). Pada tingkat pengembangan teknologi yang sama, volume output yang sama. Jelas bahwa beban yang lebih tinggi akan meningkatkan persyaratan untuk bahan (baja -> titanium?), Dan untuk mesin (suhu lain, tekanan), dan untuk rekayasa (toleransi toleransi lebih sedikit, desain lebih rumit). Jelas, ketika Q tumbuh, semuanya akan menjadi lebih mahal. Tapi berapa kali, dibandingkan dengan sepuluh ton?

Tugas ini, tentu saja, tidak sepele. Namun demikian, beberapa perkiraan untuk itu dapat diperoleh dari pertimbangan paling umum. Apa yang akan kita lakukan sekarang.

Kami memperkenalkan fungsi C ( Q ). Ini menggambarkan biaya serendah mungkin dari perangkat dengan efisiensi Q , dinyatakan dalam biaya perangkat serupa dengan massa yang sama pada Q = 1. Apa yang diketahui tentang itu?

1. C (1) = 1, menurut definisi.

2. C ( Q ) adalah fungsi kontinu, setidaknya sampai selisih massa diukur dengan potongan atom. Secara intuitif, tampaknya cukup lancar untuk memiliki beberapa turunan pertama. Saya pikir kita dapat mengakui (seperti kebanyakan fungsi fisik) bahwa ini umumnya analitis.

3. C ( Q ) adalah fungsi yang sangat meningkat. Semakin tinggi kualitas Q , semakin sulit membuat struktur, dan semakin mahal. Yaitu dC ( Q ) / dQ > 0 setidaknya untuk Q > 0.

4. Dengan Q lebih besar dari sekitar 3, C ( Q ) mulai meningkat lebih cepat daripada linear. Mengapa Karena kami melihat bahwa lebih murah bagi orang untuk membuat tiga truk untuk sepuluh ton dengan Q = 1 dari satu untuk tiga puluh dengan Q = 3. Ringkasnya, kami menulis: k * C (1) < C ( k ) untuk k > ≈3 - lainnya dalam kata-kata, C ( k ) tumbuh lebih cepat dari k , untuk k > ≈3.

5. Demikian pula, karena sepuluh pesawat dengan Q = 0,1 jelas tidak ekonomis daripada satu dengan Q = 1 (karena mereka membangun yang kedua, bukan yang pertama), untuk k > ≈3 kita memiliki: k * C (1 / k )> C (1), atau C (1 / k )> 1 / k .

6. Biaya pompa dari Shuttle mengisyaratkan bahwa setidaknya hingga Q ~ 100 nilai C ( Q ) tidak meningkat sebagai eksponen dengan indikator yang signifikan. Kalau tidak, TNA ini biayanya bukan jutaan dolar, tetapi semacam $ 10 ²⁰ , dan kita hampir tidak akan berhasil sama sekali. Yaitu C (100) berada di suatu tempat sekitar 10 ³ - 10 ⁸ , tetapi tidak semuanya 10 ¹⁵ .

7. Berapakah C (0)? Ini adalah biaya perangkat, yang masih dapat bergerak sendiri, tetapi tidak dapat mengambil kargo apa pun. Jelas, "truk" semacam itu lebih murah daripada truk penuh. Tetapi berapa kali? Sejarah menunjukkan bahwa kadang-kadang daripada puluhan atau ratusan. Sekitar 15 tahun telah berlalu dari pesawat pertama yang hanya mampu bergerak sendiri ( Q = 0) ke pengangkutan barang melalui udara. Dari mobil bensin pertama hingga truk yang cukup baik dengan Q = 1,5 ([ 120 ] + [ 130 ]), sedikit lebih. Jika perkembangan ini adalah kompleksitas yang luar biasa, itu hampir tidak akan selesai dengan cepat. Akibatnya, kesulitan pembuatan dan biaya kendaraan dengan Q = 0 seharusnya tidak sepenuhnya berbeda secara radikal dari yang di Q = 1. Oleh karena itu, kami berharap bahwa C ( 0 ) berada di suatu tempat sekitar 0,1 - 0,5.

8. Apakah fungsi ini masuk akal untuk Q negatif? Cukup! Sebuah truk dengan Q = -0,5 adalah truk yang hanya akan bergerak jika Anda melepaskan setengah dari beratnya dari menara crane. Dan Q = -1 - ini adalah troli yang mengembangkan nol traksi. Mampu mengangkut kargo hanya jika Anda membawanya. Artinya, umumnya tanpa mesin. Jelas, biayanya, jika bukan bukan nol, sangat kecil. Karena itu, tuliskan C (-1) ≈ 0.

9. Dan apa itu C (-2)? Ini adalah biaya perangkat yang perlu ditarik dengan setidaknya dua kali beratnya untuk bergerak! Ya, area Q <-1 adalah jangkar, fondasi, tiang pancang, rem. Perangkat yang menghambat gerakan. Di sana, tentu saja, ada dinamika yang sangat berbeda dan hukumnya sendiri, tetapi setidaknya kita melihat bahwa C ( Q ) tidak berakhir dengan singularitas pada Q <-1, dan bahwa di wilayah Q = -1 memiliki minimum, dan oleh karena itu, setidaknya pada Lingkungan kecil dari titik C ( Q ) ini harus berperilaku seperti parabola.

Jadi, sketsa C ( Q ) terlihat seperti ini:


Kami memperluas C ( Q ) dalam seri Taylor pada titik Q = -1:



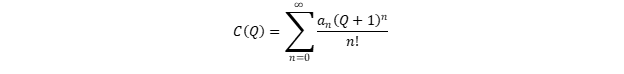
Ini mengikuti dari properti (8) bahwa ₀ = 0. Properti (4), (5) dan sebagian (9) mengisyaratkan bahwa ₁ mendekati nol, atau dalam hal apa pun, bahwa kontribusinya tidak mendominasi dalam kisaran 0 .. .3.

Dan kemudian ternyata bahwa istilah bukan nol pertama dalam ekspansi C ( Q ) parabola, dan untuk Q di wilayah unit C ( Q ) berperilaku kira-kira seperti fungsi kuadrat atau sedikit lebih cepat:

C ( Q ) ≈ a ₂ * ( Q +1) 2/2 + O (( Q + 1 ) ³ )

Dan dari [1] berarti ₂ ≈ 1/2.

Akhirnya, karena setidaknya hingga Q ~ 100 fungsi C ( Q ) masih tidak eksponensial (properti (6)), kita dapat meletakkannya di sana sama dengan Qp dengan p eksponen di suatu tempat di wilayah 2 ... 4. Lebih sulit lagi.

Kesimpulan: Untuk massa tetap, biaya perangkat C (Q) tidak meningkat lebih lemah dari (Q + 1) 2/4, tetapi tidak lebih cepat dari sekitar O (Q ⁴ ) [1]

Apakah mungkin untuk melihat ketergantungan nyata C ( Q ) untuk memahami seberapa benar kesimpulan ini? Itu sulit. Sebagian besar mekanisme yang dibuat oleh manusia adalah massa yang berbeda, tetapi tetap Q di wilayah persatuan. Kita membutuhkan yang sebaliknya: kira-kira massa yang sama, tetapi berbeda Q. Awalnya saya berharap untuk data pada mesin pesawat ... tetapi pekerjaan ^{[ 70 ] [ 80 ]} pada harga mereka sangat lucu. Harga mesin diklasifikasikan di sana, dan hanya rumus untuk prediksi dan kesalahan rata-rata yang dipublikasikan.

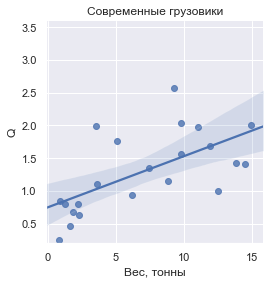
Untungnya, bantuan datang dari mobil ^{[ 150 ]} . Bersama mereka, dengan massa yang kira-kira sama, mesin dari berbagai kapasitas ditemukan. Dan meskipun daya belum merupakan muatan yang dapat diangkut, dengan beberapa upaya rekayasa, jumlahnya relatif sebanding dengan itu. Yang memungkinkan kita untuk memperkirakan apakah formula kita dekat dengan kenyataan.

Sepertinya ya:

[Sumber: [ 150 ]]

Titik biru adalah mobil sungguhan. Dalam perkiraan pertama, harga mereka naik karena kepadatan daya di tingkat 2.3.

Titik merah - harga yang dihitung dengan rumus [1], berdasarkan asumsi bahwa Q = 1 sesuai dengan mobil termurah per kilogram di kisaran $ 20-30 ribu. Dapat dilihat bahwa rumus tersebut benar-benar memberikan perkiraan C ( Q ) yang baik dari bawah (ke mana kami bertujuan).

Ketika melihat massa dari titik-titik lezat ini, ada godaan yang kuat: untuk menggambar C ( Q ) melalui mereka dan, dengan demikian, untuk mempelajari ketergantungan secara langsung. Ini tidak bisa dilakukan. Terutama karena harga mobil penumpang ditentukan tidak hanya oleh karakteristik traksinya. Sulit membayangkan sebuah mobil untuk seratus kilobaxes yang tidak memiliki AC terbaik, kursi paling nyaman, dan "asbak platinum dengan bezel berlapis rhodium". Dan semua ini membutuhkan uang yang tidak ada hubungannya dengan C ( Q ) kami. Namun, di sini “cabang” mobil yang lebih rendah, melewati hampir persis sesuai dengan perhitungan C ( Q ), terlihat menarik. Saya berani mengakui bahwa ini hanya mobil tanpa embel-embel. Di mana "tidak biji, tapi pergi." Tetapi lebih dari sekitar $ 100K untuk mobil, ini sudah tidak ada lagi.

_{Artikel ini ditulis untuk situs https://habr.com . Saat menyalin, silakan merujuk ke sumbernya. Penulis artikel ini adalah Evgeny Bobukh .}

Jadi, kami dapat memperkirakan biaya perangkat dengan Q tinggi, setidaknya dalam urutan besarnya. Mengapa ini perlu?

Tapi kenapa. Lihatlah langkah pertama dari pesawat ruang angkasa. Ya, setidaknya Proton-M ^{[ 110 ]} , untuk konkret. Dia adalah kendaraan yang hampir lengkap, dengan mesin, sistem kontrol, margin keselamatan yang layak dan berat kering 31 ton. Pada saat yang sama, pada awal roket, roket itu menyeret pada punuknya tidak hanya muatan, tetapi juga semua bahan bakar, semua tahap atas, dan, tentu saja, itu sendiri. Total - 683 ton. Ditambah mulai kelebihan beban, total (efektif) 1068 ton beban! Dari sudut pandang tahap pertama, ia bekerja dalam mode mengerikan Q = (1068/31) = 34,4! Ini setara dengan 50 ton kargo yang menumpuk di mobil penumpang.

Dan kita tahu bahwa biaya perangkat dengan Q tinggi setidaknya (Q + 1) 2/4 kali lebih tinggi daripada yang serupa dengan Q ≈ 1. Untuk Proton, ini berjumlah ... 313 kali.

Artinya, Proton seharusnya berharga 300 kali lebih banyak daripada perangkat serupa dengan Q = 1. Dan angka ini sedikit tergantung pada kemajuan dan teknologi. Karena segera setelah "ilmuwan Inggris" menemukan paduan super yang membuat roket lebih murah, maka mesin darat juga menjadi lebih murah. Karena itu, roket kimia, bahkan dapat digunakan kembali, akan selalu sangat mahal. Suka atau tidak.

Bagus Katakanlah 300 kali. Tetapi dibandingkan dengan apa ? Apakah lebih baik membandingkan perhitungan kami dengan beberapa perangkat yang ada secara objektif untuk menghilangkan kesalahan kotor?

Sayangnya, tidak ada rudal tiga puluh ton dengan Q = 1. Tetapi ada perkiraan analog yang cocok untuk perbandingan:

• Yang pertama adalah truk penambangan. Ya, bukan roket. Tapi tetap saja, itu juga mesin panas, tidak sepenuhnya rekayasa sepele, dan salah satu cara termurah untuk mengangkut barang. Dan jika kita sudah berbicara tentang eksplorasi ruang angkasa, bukankah seharusnya truk itu menjadi prototipe model bisnis pesawat ruang angkasa? Jadi mari kita coba, setidaknya untuk perkiraan umum. Berikut adalah 30 ton Belaz-7540. Harga pasar ^{[ 140 ]} adalah 3,7 juta rubel, mis. $ 62rb Untuk Proton, ini dikonversi ke biaya tahap pertama di wilayah $ 19 juta. Wikipedia adalah singkatan dari ^{[ 100 ]} biaya startup sebagai $ 65 juta. Cukup dekat, mengingat jumlah ini termasuk jauh lebih banyak, kecuali untuk harga langkah pertama.
• Pada [ 160 ] dijelaskan sebuah platform roket eksperimental pada rel. Massa 10 ton, lima langkah, berakselerasi ke 4 km / s. Harganya 750 kilobax. Dilihat oleh gambar-gambar dan parameter yang diterbitkan, perangkat ini bekerja di suatu tempat dengan Q = 10. Bukan unit, tetapi masih belum 34. Jika Anda mulai dari angka-angka ini, langkah pertama Proton akan menelan biaya $ 23 juta.
• Secara umum, ketika saya mencoba membayangkan roket dengan Q = 1, di mata pikiran saya ada semacam kekar kosong dengan takik kecil diisi dengan bubuk mesiu. Bubuk mesiu terbakar dan mendorong yang kosong ke depan. Cukup sedikit, Anda tidak akan terlalu cepat. Saya menunda gambar ini selama dua hari, sampai saya menyadari bahwa itu mengingatkan saya. Ini ... palu pneumatik! Di mana gas mengembang dan mendorong yang kosong. Bastardisasi pamungkas ide mesin jet, masih mempertahankan semacam kekerabatan. Ya, kami sedang mencari. Ya, inilah palu pneumatik Stanko M212 ^{[ 170 ]} . Berat disc adalah 2 ton, keseluruhan struktur adalah 58,3 ton. Sistem Q , oleh karena itu, adalah 0,034 sederhana. Dijual seharga 40 ribu euro. Jika kita memperkirakan biaya lelucon ini hingga Q = 34,4 sesuai dengan rumus [1], kita mendapat ... 47 juta euro. Atau 24 juta dalam proporsi lebih dari 30 ton.

Tampaknya kita tidak benar-benar bercerai dari kenyataan.

Untuk meringkas. Karena roket, bahkan yang dapat digunakan kembali, harganya 2–3 kali lipat lebih mahal daripada truk, setiap penyelesaian ruang yang terbuat dari bahan-bahan berbasis darat juga akan menelan biaya 100–1.000 kali lebih banyak daripada rekan-rekan dari darat. Ini adalah hambatan yang sangat tinggi untuk pembangunan.

Rudal itu mahal karena mereka sangat berat dan dipaksa untuk bekerja ketika mereka tidak sehat pada Q. Tapi mengapa roketnya berat? Jawabannya (yang agak lebih dalam dari rumus Tsiolkovsky) akan kita bahas di bagian kedua.

Untuk dilanjutkan .

Pembaruan: beberapa orang mencoba menunjukkan ambiguitas mengenai bahan bakar ketika mempertimbangkan rudal. Saya memikirkannya. Dan saya menyadari bahwa sebenarnya ada beberapa ketidakakuratan dalam artikel tersebut. Dilihat di komentar di sini .