Filter Kalman untuk meminimalkan nilai entropi dari kesalahan acak dengan distribusi non-Gaussian

Pendahuluan

Di Habr, deskripsi matematis tentang pengoperasian filter Kalman dan fitur penerapannya dipertimbangkan dalam publikasi berikut [1 ÷ 10]. Dalam publikasi [2], algoritma dari filter Kalman (FC) dalam model "state space" dianggap dalam bentuk yang sederhana dan dapat dimengerti. Perlu dicatat bahwa studi tentang sistem kontrol dan manajemen dalam domain waktu menggunakan variabel status telah banyak digunakan baru-baru ini karena kemudahan analisis [11]

Publikasi [8] sangat menarik minat khusus untuk pelatihan. Teknik metodis penulis sangat efektif, ia memulai artikelnya dengan mempertimbangkan distribusi kesalahan Gaussian acak, mempertimbangkan algoritma FC, dan berakhir dengan formula iteratif sederhana untuk memilih perolehan FC. Penulis membatasi dirinya pada pertimbangan distribusi Gaussian, mengutip fakta bahwa cukup besar $$$n$ (Pengukuran berganda) hukum distribusi dari jumlah variabel acak cenderung ke distribusi Gaussian.

Secara teoritis, pernyataan seperti itu tentu benar, tetapi dalam praktiknya jumlah pengukuran pada setiap titik dalam rentang tidak bisa sangat besar. Kalman RE sendiri memperoleh hasil pada kovarians minimum filter berdasarkan proyeksi ortogonal, tanpa mengasumsikan bahwa kesalahan pengukuran adalah Gaussian [12].

Tujuan dari publikasi ini adalah untuk mempelajari kemampuan filter Kalman untuk meminimalkan nilai entropi kesalahan acak dengan distribusi non-Gaussian.
Untuk mengevaluasi efektivitas filter Kalman dalam mengidentifikasi hukum distribusi atau superposisi hukum dari data eksperimen, kami menggunakan teori informasi pengukuran berdasarkan teori informasi C. Shannon, yang menurutnya informasi, seperti kuantitas fisik, dapat diukur dan dievaluasi.

Keuntungan utama dari pendekatan informasi untuk deskripsi pengukuran adalah bahwa ukuran interval entropi ketidakpastian dapat ditemukan secara matematis untuk setiap hukum distribusi. Ini menghilangkan kesewenang-wenangan yang dikembangkan secara historis yang tidak terhindarkan dengan penugasan sukarela dari berbagai nilai probabilitas kepercayaan.Hal ini sangat penting dalam proses pendidikan, ketika siswa dapat mengamati penurunan ketidakpastian pengukuran ketika menerapkan penyaringan Kalman pada sampel numerik yang diberikan [13,14].

Selain itu, kombinasi karakteristik probabilistik dan informasi sampel dapat lebih akurat menentukan sifat distribusi kesalahan acak. Ini dijelaskan oleh database ekstensif nilai numerik dari parameter seperti koefisien entropi dan counterexcess untuk berbagai undang-undang distribusi dan superposisi mereka.

Evaluasi superposisi undang-undang distribusi variabel acak dengan koefisien entropi dan counterexcess (diperoleh dari data eksperimental)

Kepadatan distribusi probabilitas untuk setiap kolom lebar histogram [14] $$$d$ sama dengan $$$p_ {i} (x_ {i}) = n_ {i} / (n \ cdot d)$ , maka estimasi probabilitas entropi didefinisikan sebagai $$$H \ kiri (x \ kanan) = \ int _ {- \ infty} ^ {+ \ infty} p \ kiri (x \ kanan) \ ln p \ kiri (x \ kanan) dx$ ketika menemukan entropi dengan histogram dari $$$m$ kolom kami mendapatkan rasio:

$$$\ displaystyle H \ kiri (x \ kanan) = - \ sum_ {i = 1} ^ {m} \ int _ {\ tilde {x_ {i}} - \ frac {d} {2}} ^ {\ tilde { x_ {i}} + \ frac {d} {2}} \ frac {n_ {i}} {nd} \ ln \ frac {n_ {i}} {nd} = \ sum_ {i = 1} ^ {m } \ frac {n_ {i}} {n} \ ln \ frac {n} {n_ {i}} + \ ln d$

Kami menyajikan ekspresi untuk memperkirakan entropi dalam bentuk:

$$$H \ kiri (x \ kanan) = \ ln \ kiri [d \ prod_ {i = 1} ^ {m} \ kiri (\ frac {n} {n_ {i}} \ kanan) ^ {\ frac {n_ {i}} {n}} \ kanan]$

Kami memperoleh ekspresi untuk memperkirakan nilai entropi dari variabel acak:

$$$\ Delta _ {e} = \ frac {1} {2} e ^ {H \ kiri (x \ kanan)} = \ frac {dn} {2} 10 ^ {- \ frac {1} {n} \ sum_ {1} ^ {m} n_ {i} \ lg n_ {i}}$

Klasifikasi undang-undang distribusi dilakukan di pesawat dalam koordinat koefisien entropi $$$k = \ frac {\ Delta _ {e}} {\ sigma}$ dan counterexcess $$$\ psi = \ frac {\ sigma ^ {2}} {\ sqrt {\ mu _ {4}}}$ dimana $$$\ mu _ {4} = \ frac {1} {n} \ sum_ {1} ^ {n} \ kiri (x_ {i} - \ bar {X} \ kanan) ^ {4}$ .

Untuk semua undang-undang distribusi yang mungkin, \ psi bervariasi dari 0 hingga 1, dan k dari 0 hingga 2.066, sehingga setiap hukum dapat dikarakteristikkan dengan titik tertentu. Kami menunjukkan ini menggunakan program berikut:




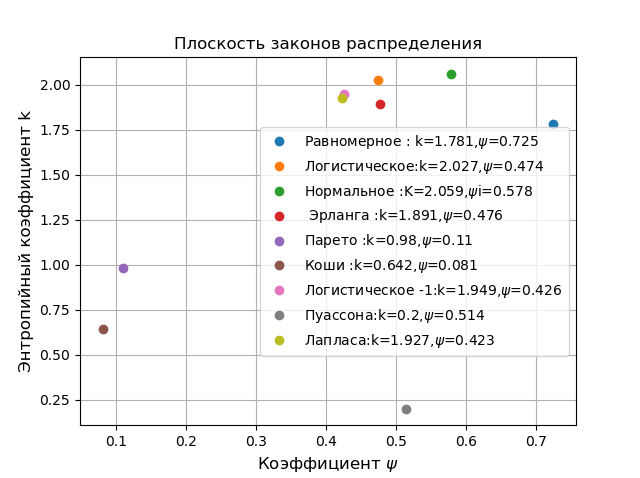
Di pesawat dalam koordinat $$$k, \ psi$ dihapus dari sisa distribusi, Pareto, distribusi Cauchy, meskipun mereka milik berbagai bidang aplikasi, yang pertama dalam fisika dan yang kedua di bidang ekonomi. Sebagai perbandingan, pilih distribusi Gaussian normal di bagian atas klasifikasi. Semua perbandingan di bawah ini dilakukan pada sampel terbatas dan sifat menunjukkan kemampuan kristal fotonik menggunakan contoh penentuan numerik dari kesalahan entropi.

Memilih Algoritma Filter Kalman

Pada setiap titik yang dipilih dalam rentang pengukuran, beberapa pengukuran dilakukan dan hasilnya dibandingkan dengan ukuran yang FC “tidak tahu”. Karena itu, Anda harus memilih FC, misalnya Kalman Filter untuk Memperkirakan Konstan [16]. Namun, saya lebih suka Python dan memilih opsi [16] dengan dokumentasi yang luas. Saya akan memberikan deskripsi algoritma:

Karena konstanta selalu satu model sistem dapat direpresentasikan sebagai:

$$$x_ {k} = x_ {k-1} + w_ {k}$ , (1)

Untuk model, matriks transisi merosot menjadi satu, dan matriks kontrol menjadi nol. Model pengukuran berupa:

$$$y_ {k} = y_ {k-1} + v_ {k}$ , (2)

Untuk model (2), matriks pengukuran dikonversi menjadi satu, dan matriks kovarians $$$P, Q, R$ berubah menjadi dispersi. Selanjutnya $$$k$ Langkah ke-2, sebelum hasil pengukuran tiba, filter skalar Kalman mencoba untuk mengevaluasi keadaan baru sistem menggunakan rumus (1):

$$$\ hat {x} _ {k / (k-1)} = \ hat {x} _ {(k-1) / (k-1)}$ , (3)

Persamaan (3) menunjukkan bahwa estimasi a priori pada langkah berikutnya sama dengan estimasi posterior yang dibuat pada langkah sebelumnya. Perkiraan apriori dari varian kesalahan:

$$$P_ {k / (k-1)} = P _ {(k-1) / (k-1)} + Q_ {k}$ , (4)

Menurut penilaian negara apriori $$$\ hat {x} _ {k / (k-1)}$ adalah mungkin untuk menghitung perkiraan pengukuran:

$$$\ hat {y} _ {k} = \ hat {x} _ {k / (k-1)}$ , (5)

Setelah pengukuran selanjutnya diterima $$$y_ {k}$ , filter menghitung kesalahan perkiraannya $$$k$ pengukuran th:

$$$e_ {k} = y_ {k} - \ hat {y} _ {k} = y_ {k} - \ hat {x} _ {k / (k-1)}$ , (6)

Filter menyesuaikan penilaiannya tentang kondisi sistem, memilih titik yang terletak di suatu tempat di antara penilaian awal $$$\ hat {x} _ {k / (k-1)}$ dan titik yang sesuai dengan dimensi baru $$$y_ {k}$ :

$$$e_ {k} = y_ {k} - \ hat {y} _ {k} = y_ {k} - \ hat {x} _ {k / (k-1)}$ , (7)

dimana $$$G _ {k}$ - gain filter.

Perkiraan varians kesalahan juga diperbaiki:

$$$P_ {k / (k)} = (1-G_ {k}) \ cdot P_ {k / (k-1)}$ , (8)

Dapat dibuktikan bahwa varians kesalahan $$$e_ {k}$ sama dengan:

$$$S_ {k} = P_ {k / (k-1)} + R_ {k}$ , (9)

Gain dari filter, di mana kesalahan minimum dalam menilai keadaan sistem dicapai, ditentukan dari hubungan:

$$$G_ {k} = P_ {k / (k-1)} / S_ {k}$ , (10)

Minimalisasi kesalahan entropi FC untuk kebisingan dengan distribusi Cauchy, Pareto, dan Gaussian

1. Dalam teori probabilitas, kepadatan distribusi Cauchy ditentukan dari hubungan:

$$$f (x) = \ frac {b} {\ pi \ cdot (1-x ^ {2})}$

Untuk distribusi ini, tidak mungkin untuk memperkirakan kesalahan dengan metode teori probabilitas ( $$$\ sigma = \ infty$ ) tetapi teori informasi memungkinkan Anda melakukan ini:




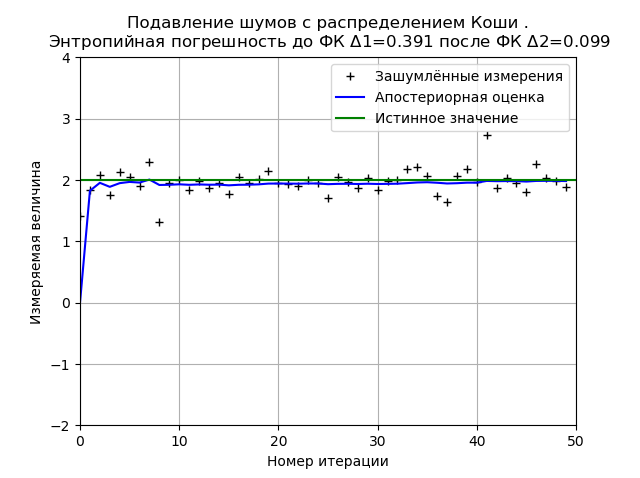
Jenis grafik dapat berubah baik ketika program dimulai kembali (generasi baru dari sampel distribusi), dan tergantung pada jumlah pengukuran dan parameter distribusi, tetapi satu tetap tidak berubah. FC meminimalkan nilai kesalahan entropi yang dihitung berdasarkan teori informasi pengukuran. Untuk grafik yang diberikan, FC mengurangi kesalahan entropi sebesar 3,9 kali.

2. Dalam teori probabilitas, kepadatan distribusi Pareto dengan parameter $$$x_ {m}$ dan $$$k$ ditentukan dari rasio:

$$

$$f_ {X} (x) = \ kiri \ {\ begin {matrix} \ frac {kx_ {k} ^ {m}} {x ^ {k + 1}}, & x \ geq x_ {m} \\ 0, & x <x_ {m} \ end {matrix} \ benar.$$

Perlu dicatat bahwa distribusi Pareto ditemukan tidak hanya dalam perekonomian. Anda dapat memberikan contoh distribusi ukuran file berikut dalam lalu lintas Internet melalui protokol TCP.

3. Dalam teori probabilitas, kepadatan distribusi normal (Gaussian) dengan ekspektasi matematis $$$\ mu$ dan standar deviasi $$$\ sigma$ ditentukan dari rasio:

$$$f (x) = \ frac {1} {\ sigma \ sqrt {2 \ pi}} \ cdot e ^ {- \ frac {(x- \ mu) ^ {2}} {2 \ sigma ^ {2} }}$

Penentuan minimalisasi kesalahan entropi FC dari kebisingan dengan distribusi Gaussian diberikan untuk perbandingan dengan distribusi non-Gaussian Cauchy dan Pareto.




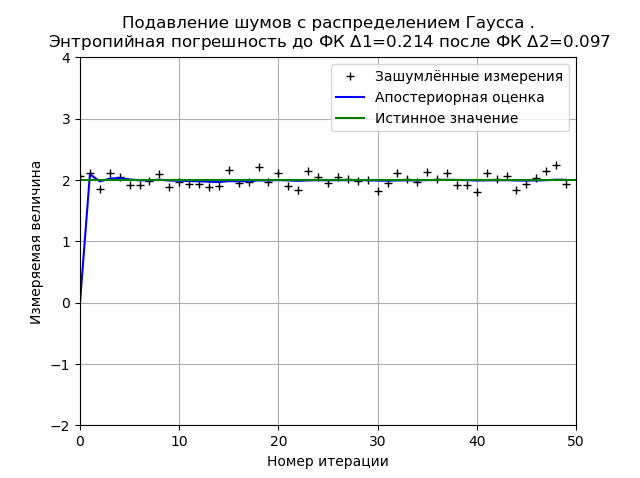
Distribusi Gaussian memberikan stabilitas hasil yang lebih tinggi untuk 50 pengukuran dan untuk grafik yang ditunjukkan, kesalahan entropi berkurang sebesar 2,2 kali.

Meminimalkan kesalahan entropi FC dari sampel data eksperimental dengan undang-undang distribusi kebisingan yang tidak diketahui




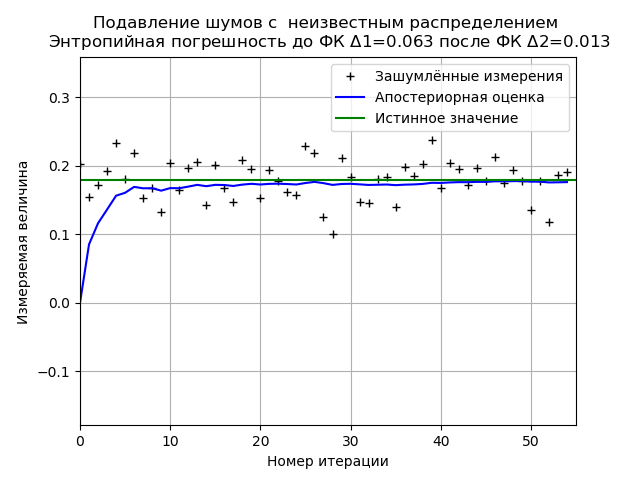
Saat menganalisis sampel data eksperimental, kami memperoleh hasil yang stabil untuk meminimalkan kesalahan entropi FC. Untuk sampel ini, FC mengurangi kesalahan entropi sebesar 4,85 kali.

Kesimpulan

Semua perbandingan dalam artikel ini dilakukan pada sampel data yang terbatas, oleh karena itu, kesimpulan mendasar harus dipertahankan, namun, penggunaan kesalahan entropi memungkinkan kami untuk mengukur efektivitas filter Kalman dalam implementasi yang diberikan, oleh karena itu, tugas pelatihan artikel ini dapat dianggap selesai.