Estimasi orientasi spasial, atau Bagaimana tidak perlu takut dengan filter Mahoney dan Majwik

Apa yang kita bicarakan

Munculnya Habre di sebuah pos tentang filter Majwik adalah peristiwa simbolis dengan caranya sendiri. Rupanya, antusiasme umum untuk drone menghidupkan kembali minat dalam tugas menilai orientasi tubuh dengan pengukuran inersia. Pada saat yang sama, metode tradisional berdasarkan filter Kalman berhenti memuaskan publik - baik karena persyaratan tinggi untuk sumber daya komputasi yang tidak dapat diterima untuk drone, atau karena pengaturan yang kompleks dan tidak intuitif.

Pos disertai dengan implementasi yang sangat kompak dan efisien dari filter pada C. Namun, dilihat dari komentar, makna fisik dari kode ini, serta seluruh artikel, tetap samar bagi seseorang. Yah, kami dengan jujur ​​mengakui: filter Majwik adalah yang paling rumit dari grup filter berdasarkan pada prinsip yang sangat sederhana dan elegan. Saya akan mempertimbangkan prinsip-prinsip ini dalam posting saya. Kode tidak akan ada di sini. Posting saya bukan cerita tentang implementasi spesifik dari algoritma estimasi orientasi, melainkan undangan untuk menemukan variasi Anda sendiri pada topik tertentu, yang bisa sangat banyak.

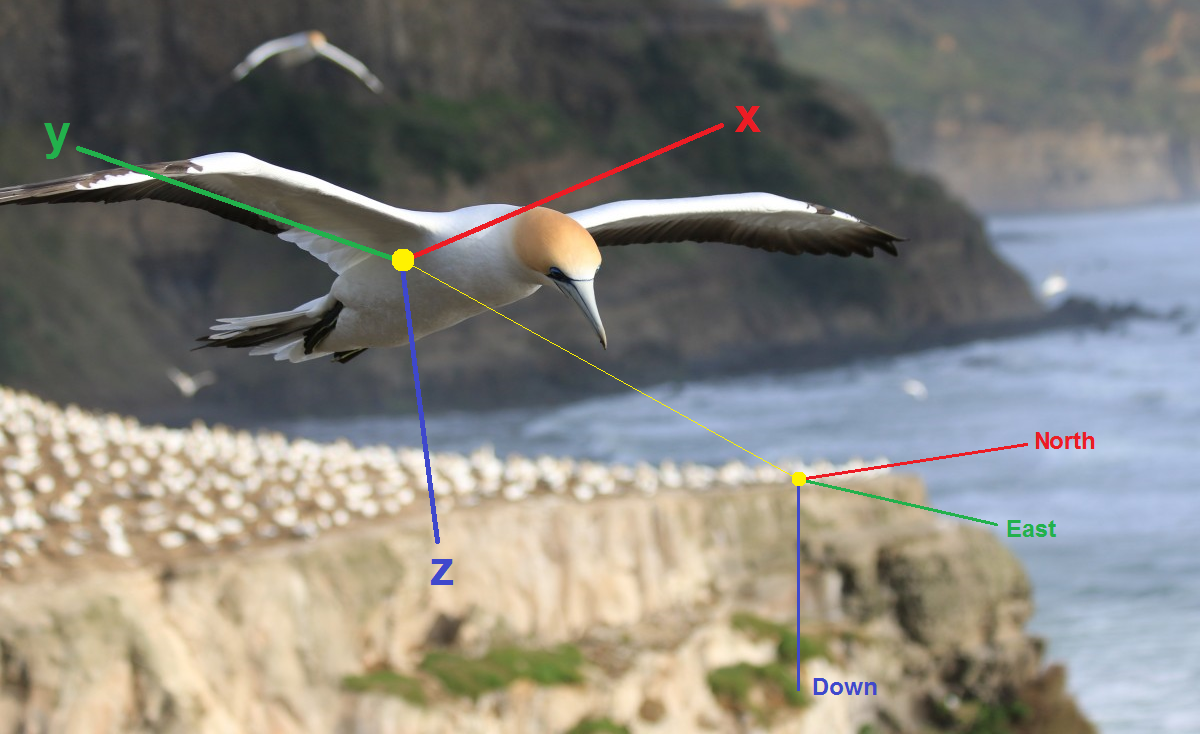
Tampilan orientasi

Ingat kembali dasar-dasarnya. Untuk menilai orientasi benda di ruang, pertama-tama Anda harus memilih beberapa parameter yang bersama-sama menentukan orientasi ini, mis. pada dasarnya orientasi sistem koordinat terkait $$$xyz$ sistem yang relatif bersyarat tetap - misalnya, sistem geografis NED (Utara, Timur, Bawah). Maka Anda perlu membuat persamaan kinematik, mis. menyatakan laju perubahan parameter ini melalui kecepatan sudut dari giroskop. Akhirnya, kita perlu memasukkan pengukuran vektor dari accelerometer, magnetometer, dll ke dalam perhitungan. Berikut adalah cara paling umum untuk mewakili orientasi:

Sudut Euler - roll (roll, $$$\ phi$ ), pitch (pitch, $$$\ theta$ ), tentu saja (pos, $$$\ psi$ ) Ini adalah set parameter orientasi yang paling intuitif dan paling ringkas: jumlah parameter persis sama dengan jumlah derajat kebebasan rotasi. Untuk sudut-sudut ini, kita dapat menulis persamaan kinematik Euler . Mereka sangat menyukai mekanika teoretis, tetapi dalam masalah navigasi mereka jarang digunakan. Pertama, mengetahui sudut tidak memungkinkan mengkonversi secara langsung komponen dari vektor apa pun dari yang terhubung ke sistem koordinat geografis atau sebaliknya. Kedua, pada nada ± 90 derajat, persamaan kinematik merosot, gulungan dan arah menjadi tidak terbatas.

Rotation Matrix - Matrix $$$\ mathbf {C}$ Ukuran 3 × 3, dengan mana Anda perlu melipatgandakan vektor apa pun dalam sistem koordinat terkait untuk mendapatkan vektor yang sama dalam sistem geografis: $$$\ mathbf {r} _ {NED} = \ mathbf {C} \ mathbf {r} _ {xyz}$ . Matriks selalu ortogonal, mis. $$$\ mathbf {C} = \ mathbf {C} ^ {T}$ . Persamaan kinematik untuk itu memiliki bentuk $$$\ dot {\ mathbf {C}} = \ mathbf {C} \ mathbf {\ Omega}$ .
Di sini $$$\ mathbf {\ Omega}$ - matriks komponen kecepatan sudut yang diukur oleh giroskop dalam sistem koordinat yang terhubung:

$$

$$\ mathbf {\ Omega} = \ begin {bmatrix} 0 & - \ omega_ {z} & \ omega_ {y} \\ \ omega_ {z} & 0 & - \ omega_ {x} \\ - \ omega_ {y } & \ omega_ {x} & 0 \\ \ end {bmatrix}$$

Matriks rotasi sedikit kurang jelas dari sudut Euler, tetapi tidak seperti mereka, ini memungkinkan Anda untuk secara langsung mengkonversi vektor dan tidak kehilangan makna pada posisi sudut mana pun. Dari sudut pandang komputasi, kelemahan utamanya adalah redundansi: demi tiga derajat kebebasan, sembilan parameter diperkenalkan sekaligus, dan semuanya perlu diperbarui sesuai dengan persamaan kinematik. Masalahnya dapat sedikit disederhanakan dengan menggunakan ortogonalitas dari matriks.

Angka empat rotasi adalah obat radikal tetapi sangat tidak intuitif terhadap redundansi dan degenerasi. Ini adalah objek empat komponen. $$$\ mathbf {q} = q_ {0} + q_ {1} \ mathbf {i} + q_ {2} \ mathbf {j} + q_ {3} \ mathbf {k}$ - bukan angka, bukan vektor, dan bukan matriks. Angka empat dapat dilihat dari dua sudut. Pertama, bagaimana dengan jumlah formal skalar $$$q_ {0}$ dan vektor $$$q_ {1} \ mathbf {i} + q_ {2} \ mathbf {j} + q_ {3} \ mathbf {k}$ dimana $$$\ mathbf {i}, \ mathbf {j}, \ mathbf {k}$ - vektor sumbu satuan (yang, tentu saja, terdengar tidak masuk akal). Kedua, sebagai generalisasi bilangan kompleks, di mana sekarang kita menggunakan bukan hanya satu, tetapi tiga unit imajiner yang berbeda $$$\ mathbf {i}, \ mathbf {j}, \ mathbf {k}$ (yang terdengar tidak kalah absurd). Bagaimana angka empat terkait dengan belokan? Melalui teorema Euler: sebuah benda selalu dapat ditransfer dari satu orientasi yang diberikan ke yang lain dengan satu rotasi terbatas pada beberapa sudut $$$\ alpha$ sekitar beberapa sumbu dengan vektor panduan $$$\ mathbf {u}$ . Sudut dan sumbu ini dapat dikombinasikan menjadi angka empat: $$$\ mathbf {q} = \ mathrm {cos} (\ alpha / 2) + \ mathbf {u} \ mathrm {sin} (\ alpha / 2)$ . Seperti sebuah matriks, angka empat dapat digunakan untuk secara langsung mengkonversi vektor dari satu sistem koordinat ke yang lain: $$$\ mathbf {r} _ {NED} = \ mathbf {q} \ mathbf {r} _ {xyz} {\ mathbf {q}} ^ {- 1}$ . Seperti yang Anda lihat, representasi orientasi angka empat juga menderita redundansi, tetapi jauh lebih sedikit daripada matriks: parameter tambahan hanya satu. Tinjauan komprehensif angka empat sudah ada di Habré . Mereka berbicara tentang geometri dan grafik 3D. Kami juga tertarik pada kinematika, karena laju perubahan angka empat harus terkait dengan kecepatan sudut yang diukur. Persamaan kinematik yang sesuai memiliki bentuk $$$\ dot {\ mathbf {q}} = 1/2 \ mathbf {q} \ mathbf {\ omega}$ dimana vektornya $$$\ mathbf {\ omega}$ juga dianggap sebagai angka empat dengan bagian skalar nol.

Skema Filter

Pendekatan yang paling naif untuk menghitung orientasi adalah mempersenjatai diri Anda dengan persamaan kinematik dan memperbarui sesuai dengan itu setiap set parameter yang kita suka. Misalnya, jika kita memilih matriks rotasi, kita dapat menulis siklus dengan sesuatu dalam semangat C += * Omega * dt . Hasilnya akan mengecewakan. Giroskop, terutama MEMS, memiliki offset nol yang besar dan tidak stabil - sebagai hasilnya, bahkan dalam keadaan istirahat penuh, orientasi yang dihitung akan memiliki kesalahan akumulasi tak terbatas (drift). Semua trik yang ditemukan oleh Mahoney, Majwick, dan banyak lainnya, tidak termasuk saya, ditujukan untuk mengkompensasi penyimpangan ini dengan melibatkan pengukuran dari akselerometer, magnetometer, penerima GNSS, lag, dll. Maka lahirlah seluruh keluarga filter orientasi, berdasarkan prinsip dasar yang sederhana.

Prinsip dasar. Untuk mengimbangi penyimpangan orientasi, perlu untuk menambah kecepatan sudut yang diukur oleh giroskop, kontrol tambahan kecepatan sudut yang dibangun berdasarkan pengukuran vektor sensor lain. Vektor kecepatan sudut kontrol harus berusaha untuk menggabungkan arah vektor yang diukur dengan arah sebenarnya yang diketahui.

Pendekatan yang sama sekali berbeda diambil di sini daripada dalam membangun istilah koreksi dari filter Kalman. Perbedaan utama adalah bahwa kecepatan sudut kontrol bukan istilah, tetapi faktor untuk nilai estimasi (matriks atau angka empat). Keuntungan penting mengikuti dari ini:

• Filter evaluasi dapat dibangun untuk orientasi itu sendiri, dan bukan untuk penyimpangan kecil dari orientasi dari yang disediakan oleh giroskop. Selain itu, nilai estimasi akan secara otomatis memenuhi semua persyaratan yang diberikan oleh tugas: matriks akan menjadi orthogonal, angka empat dinormalisasi.
• Arti fisik dari kecepatan sudut kontrol jauh lebih jelas daripada istilah koreksi dalam filter Kalman. Semua manipulasi dilakukan dengan vektor dan matriks dalam ruang fisik tiga dimensi biasa, dan bukan dalam ruang keadaan multidimensi abstrak. Ini sangat menyederhanakan penyempurnaan dan penyesuaian filter, dan sebagai bonus itu memungkinkan Anda untuk menyingkirkan matriks dimensi besar dan perpustakaan matriks berat.

Sekarang mari kita lihat bagaimana ide ini diimplementasikan dalam opsi filter tertentu.

Filter mahoney. Semua matematika marah dari artikel Mahoney asli ditulis untuk membenarkan persamaan sederhana (32). Kami menulis ulang mereka dalam notasi kami. Jika kita mengabaikan estimasi perpindahan nol giroskop, maka dua persamaan utama tetap - persamaan kinematik untuk matriks rotasi itu sendiri (dengan kecepatan sudut kontrol dalam bentuk matriks $$$\ mathbf {\ Omega} '$ ) dan hukum pembentukan kecepatan ini dalam bentuk vektor $$$\ mathbf {\ omega} '$ . Untuk kesederhanaan, kami mengasumsikan bahwa tidak ada akselerasi atau pickup magnetik, dan berkat ini, pengukuran akselerasi jatuh bebas tersedia bagi kami. $$$- \ hat {\ mathbf {g}} _ {xyz}$ dari akselerometer dan medan magnet Bumi $$$\ hat {\ mathbf {m}} _ {xyz}$ dari magnetometer. Kedua vektor diukur oleh sensor dalam sistem koordinat yang terhubung, dan dalam sistem geografis posisi mereka diketahui: $$$- \ mathbf {g} _ {NED}$ menunjuk ke atas $$$\ mathbf {m} _ {NED}$ - ke utara magnet. Maka persamaan filter Mahoney akan terlihat seperti ini:

$$

$$\ dot {\ mathbf {C}} = \ mathbf {C} (\ mathbf {\ Omega} + \ mathbf {\ Omega} ') \\ \ mathbf {\ omega'} = k_ {g} \ hat {\ mathbf {g}} _ {xyz} \ times \ mathbf {C} ^ {T} \ mathbf {g} _ {NED} + k_ {m} \ hat {\ mathbf {m}} _ {xyz} \ times \ mathbf {C} ^ {T} \ mathbf {m} _ {NED}$$

Mari kita perhatikan dengan seksama persamaan kedua. Istilah pertama di sisi kanan adalah produk vektor. Faktor pertama di dalamnya adalah percepatan gravitasi yang terukur, yang kedua benar. Karena faktor harus berada dalam satu sistem koordinat, faktor kedua dikonversi ke sistem yang terhubung dengan mengalikannya $$$\ mathbf {C} ^ {T}$ . Kecepatan sudut, dikonstruksikan sebagai produk vektor, tegak lurus terhadap bidang vektor faktor. Ini memungkinkan Anda untuk memutar posisi yang diperkirakan dari sistem koordinat terkait hingga vektor faktor bertepatan dalam arah - maka produk vektor akan diatur ulang ke nol dan rotasi akan berhenti. Koefisien $$$k_ {g}$ mengatur kekakuan dari umpan balik tersebut. Istilah kedua melakukan operasi yang sama dengan vektor magnetik. Faktanya, filter Mahoney mewujudkan tesis terkenal: pengetahuan tentang dua vektor noncollinear dalam dua sistem koordinat yang berbeda memungkinkan Anda untuk secara unik mengembalikan orientasi timbal balik dari sistem ini. Jika ada lebih dari dua vektor, maka ini akan memberikan redundansi pengukuran yang berguna. Jika hanya ada satu vektor, maka satu derajat kebebasan rotasi (pergerakan di sekitar vektor ini) tidak dapat diperbaiki. Misalnya, jika hanya vektor yang diberikan $$$- \ mathbf {g}$ , maka Anda dapat menyesuaikan drift dari roll and pitch, tetapi tidak tentu saja.

Tentu saja, filter Mahoney tidak harus menggunakan matriks rotasi. Ada juga varian angka empat noncanonical.

Platform gyro virtual. Dalam filter Mahoney, kami menerapkan kecepatan sudut kontrol $$$\ mathbf {\ omega '}$ ke sistem koordinat terkait. Tetapi Anda dapat menerapkannya pada perkiraan posisi sistem koordinat geografis. Persamaan kinematik kemudian mengambil bentuk

$$

$$\ dot {\ mathbf {C}} = \ mathbf {C} \ mathbf {\ Omega} - \ mathbf {\ Omega} '\ mathbf {C}$$

Ternyata pendekatan ini membuka jalan bagi analogi fisik yang sangat bermanfaat. Cukuplah untuk mengingat kembali teknik gyroscopic yang dimulai dengan - sistem navigasi vertikal dan inersia berdasarkan platform yang distabilkan gyro dalam gimbal.


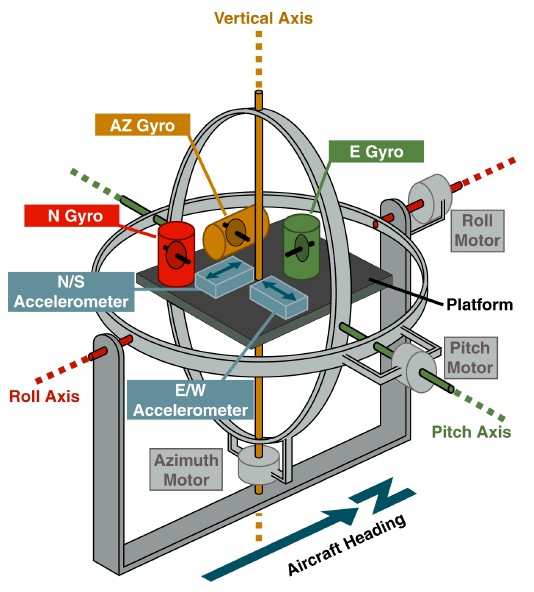www.theairlinepilots.com

Tujuan dari platform ini adalah terwujudnya sistem koordinat geografis. Orientasi pembawa diukur relatif terhadap platform ini dengan sensor sudut pada frame suspensi. Jika giroskop memiliki drift, maka platform juga melayang setelah mereka, dan kesalahan terakumulasi dalam pembacaan sensor sudut. Untuk menghilangkan kesalahan ini, umpan balik diperkenalkan dari accelerometer yang diinstal pada platform. Sebagai contoh, penyimpangan platform dari cakrawala di sekitar sumbu utara dirasakan oleh akselerometer sumbu timur. Sinyal ini memungkinkan pengaturan kecepatan sudut kontrol $$$\ mathbf {\ omega '}$ mengembalikan platform ke cakrawala.

Kita dapat menggunakan konsep visual yang sama dalam tugas kita. Persamaan kinematik yang diuraikan kemudian harus dibaca sebagai berikut: laju perubahan orientasi adalah perbedaan antara dua gerakan rotasi - gerakan absolut pembawa (istilah pertama) dan gerak absolut dari platform gyro virtual (istilah kedua). Analogi dapat diperluas ke hukum pembentukan kecepatan sudut pengontrol. Vektor $$$- \ hat {\ mathbf {g}} _ {NED} = - \ mathbf {C} \ hat {\ mathbf {g}} _ {xyz}$ Ini mewakili kesaksian akselerometer, konon berdiri di atas platform gyro. Kemudian, untuk alasan fisik, Anda dapat menulis:

$$

$$\ omega '_ {N} = - gk_ {g} \ hat {g} _ {E}, \; \ omega '_ {E} = gk_ {g} \ hat {g} _ {N}$$

Dimungkinkan untuk mencapai hasil yang persis sama dengan cara formal, dengan membuat penggandaan vektor dalam semangat filter Mahoney, tetapi sekarang tidak dalam terhubung, tetapi dalam sistem koordinat geografis. Apakah ini hanya perlu?

Petunjuk pertama dari analogi yang berguna antara platform dan navigasi inersia strapdown muncul, tampaknya, dalam paten Boeing kuno . Kemudian ide ini secara aktif dikembangkan oleh Salychev , dan baru-baru ini - oleh saya juga . Keuntungan nyata dari pendekatan ini:

• Kecepatan sudut kontrol dapat dibentuk berdasarkan prinsip-prinsip fisik yang dapat dimengerti.
• Secara alami, saluran horisontal dan terarah, yang sangat berbeda dalam sifat dan metode koreksi, dipisahkan. Di filter Mahoney mereka dicampur.
• Lebih mudah untuk mengkompensasi efek akselerasi karena penggunaan data GNSS, yang dikeluarkan secara tepat dalam sumbu geografis daripada sumbu terkait.
• Sangat mudah untuk menggeneralisasi algoritma untuk kasus navigasi inertial presisi tinggi, di mana perlu untuk memperhitungkan bentuk dan rotasi Bumi. Bagaimana melakukan ini dalam skema Mahoney, saya tidak bisa membayangkan.

Filter Majwick. Majwik memilih jalan yang sulit . Jika Mahoney, tampaknya, secara intuitif sampai pada keputusannya, dan kemudian membenarkannya secara matematis, maka Majwik sejak awal membuktikan dirinya sebagai seorang formalis. Dia berusaha menyelesaikan masalah optimisasi. Dia beralasan seperti itu. Atur orientasi angka empat rotasi. Dalam kasus ideal, arah yang dihitung dari beberapa vektor yang diukur (mari kita memilikinya $$$- \ mathbf {g}$ ) bertepatan dengan yang benar. Maka akan menjadi $$${\ mathbf {q}} ^ {- 1} \ mathbf {g} _ {NED} \ mathbf {q} = \ hat {\ mathbf {g}} _ {xyz}$ . Pada kenyataannya, ini tidak selalu dapat dicapai (terutama jika ada lebih dari dua vektor), tetapi Anda dapat mencoba untuk meminimalkan penyimpangan $$$\ mathbf {F} = {\ mathbf {q} ^ {- 1} \ mathbf {g} _ {NED} \ mathbf {q}} - \ hat {\ mathbf {g}} _ {xyz}$ dari kesetaraan yang tepat. Untuk melakukan ini, kami memperkenalkan kriteria minimalisasi

$$

$$E = \ frac {1} {2} | \ mathbf {F} | ^ {2} \ rightarrow \ mathrm {min}$$

Minimalisasi memerlukan gradient descent - bergerak dalam langkah-langkah kecil ke arah yang berlawanan dengan gradient $$$\ nabla E$ , yaitu berlawanan dengan peningkatan fungsi tercepat $$$E$ . Ngomong-ngomong, Majwik membuat kesalahan: dalam semua karyanya ia tidak memperkenalkan $$$E$ dan terus-menerus menulis $$$\ nabla \ mathbf {F}$ bukannya $$$\ nabla E$ , meskipun sebenarnya menghitung dengan tepat $$$\ nabla E$ .

Akibatnya, gradient descent mengarah ke kondisi berikut: untuk mengimbangi penyimpangan orientasi, istilah negatif baru yang sebanding dengan persamaan kinematik harus ditambahkan dari persamaan kinematik $$$\ nabla E$ :

$$

$$\ dot {\ mathbf {q}} = \ frac {1} {2} \ mathbf {q} \ mathbf {\ omega} - \ beta \ frac {\ nabla E} {| \ nabla E |} $$$

Di sini Majwik menyimpang sedikit dari "prinsip dasar" kami: ia tidak menambahkan istilah koreksi ke kecepatan sudut, tetapi ke tingkat perubahan angka empat, dan ini bukan hal yang persis sama. Akibatnya, mungkin ternyata angka empat yang diperbarui berhenti menjadi tunggal dan, karenanya, kehilangan kemampuan untuk mewakili orientasi. Oleh karena itu, untuk filter Majwik, normalisasi artifisial dari angka empat adalah operasi vital, sedangkan untuk filter lain diinginkan, bukan opsional.

Efek akselerasi

Sampai sekarang, telah diasumsikan bahwa tidak ada akselerasi sejati dan akselerometer hanya mengukur percepatan gravitasi $$$- \ mathbf {g}$ . Ini memungkinkan untuk mendapatkan standar vertikal dan, dengan bantuannya, mengimbangi roll and pitch drift. 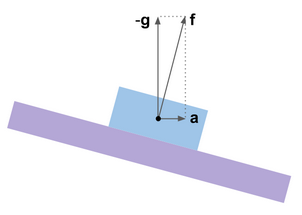Namun, dalam kasus umum, akselerometer, terlepas dari prinsip operasinya, mengukur percepatan yang terlihat - perbedaan vektor percepatan sejati dan percepatan gravitasi $$$\ mathbf {f} = \ mathbf {a} - \ mathbf {g}$ . Arah percepatan yang terlihat tidak sesuai dengan yang vertikal, dan kesalahan yang disebabkan oleh percepatan muncul dalam perkiraan roll and pitch.

Ini mudah untuk diilustrasikan menggunakan analogi platform gyro virtual. Sistem koreksinya dirancang sedemikian rupa sehingga platform berhenti pada posisi sudut di mana sinyal akselerometer, yang seharusnya dipasang di atasnya, diatur ulang ke nol, mis. saat vektor diukur $$$\ mathbf {f}$ menjadi tegak lurus terhadap sumbu sensitivitas accelerometer. Jika tidak ada akselerasi, posisi ini bertepatan dengan horizon. Ketika akselerasi horizontal terjadi, platform gyro dibelokkan. Kita dapat mengatakan bahwa platform gyro mirip dengan pendulum atau garis tegak lurus yang sangat teredam.



Dalam komentar di pos tentang filter Majwik, sebuah pertanyaan muncul di sekitar apakah mungkin untuk berharap bahwa filter ini kurang rentan terhadap akselerasi daripada, misalnya, filter Mahoney. Sayangnya, semua filter yang dijelaskan di sini mengeksploitasi prinsip fisik yang sama dan karenanya menderita masalah yang sama. Tidak mungkin menipu fisika dengan matematika. Lalu apa yang harus dilakukan?

Cara paling sederhana dan paling sulit ditemukan pada pertengahan abad terakhir untuk penerbangan-vertikal penerbangan: untuk mengurangi atau sama sekali nol kecepatan kontrol sudut di hadapan percepatan atau kecepatan sudut saja (yang menunjukkan masuknya belokan). Metode yang sama dapat diterapkan pada sistem platform saat ini. Dalam hal ini, akselerasi harus dinilai dari nilainya $$$\ hat {f} _ {N}, \ hat {f} _ {E}$ tapi tidak $$$\ hat {f} _ {x}, \ hat {f} _ {y}$ yang pada gilirannya adalah nol. Namun dalam ukuran $$$\ hat {\ mathbf {f}} _ {NED}$ tidak selalu mungkin untuk membedakan percepatan sejati dari proyeksi percepatan gravitasi, yang disebabkan oleh kecenderungan platform gyro, yang harus dihilangkan. Oleh karena itu, metode ini tidak berfungsi dengan baik - tetapi tidak memerlukan sensor tambahan.

Metode yang lebih akurat didasarkan pada penggunaan pengukuran kecepatan eksternal dari penerima GNSS. Jika kecepatan diketahui $$$\ mathbf {v}$ , maka dapat dibedakan secara numerik dan mendapatkan akselerasi sejati $$$\ dot {\ mathbf {v}}$ . Lalu bedanya $$$\ hat {\ mathbf {f}} _ {NED} - \ dot {\ mathbf {v}}$ akan persis sama $$$- \ hat {\ mathbf {g}} _ {NED}$ terlepas dari pergerakan media. Dapat digunakan sebagai standar vertikal. Misalnya, Anda dapat menentukan kecepatan sudut kontrol platform gyro dalam formulir

$$

$$\ omega '_ {N} = gk_ {g} (\ hat {f} _ {E} - \ dot {v} _ {E}), \; \ omega '_ {E} = - gk_ {g} (\ hat {f} _ {N} - \ dot {v} _ {N})$$

Sensor Zero Offsets

Fitur menyedihkan giroskop dan akselerometer tingkat konsumen adalah ketidakstabilan besar dari offset nol dalam waktu dan suhu. Untuk menghilangkannya, kalibrasi pabrik atau laboratorium saja tidak cukup - Anda perlu mengevaluasi kembali selama operasi.

Giroskop. Kami akan berurusan dengan nol offset giroskop $$$\ delta {\ mathbf {\ omega}}$ . Posisi yang diperkirakan dari sistem koordinat yang terkait bergerak menjauh dari posisi aslinya dengan kecepatan sudut yang ditentukan oleh dua faktor yang berlawanan - nol perpindahan giroskop dan mengendalikan kecepatan sudut: $$$\ delta {\ mathbf {\ omega}} - \ mathbf {\ omega '}$ . Jika sistem koreksi (misalnya, dalam filter Mahoney) berhasil menghentikan pintu keluar, maka dalam kondisi mantap akan terjadi $$$\ delta {\ mathbf {\ omega}} = \ mathbf {\ omega '}$ . Dengan kata lain, dalam kontrol kecepatan sudut $$$\ mathbf {\ omega '}$ informasi tentang gangguan valid yang tidak diketahui $$$\ delta {\ mathbf {\ omega}}$ . Oleh karena itu, estimasi kompensasi dapat diterapkan: kita tidak mengetahui besarnya gangguan secara langsung, namun, kita tahu tindakan korektif apa yang diperlukan untuk menyeimbangkannya. Ini adalah dasar untuk memperkirakan nol perpindahan giroskop. Misalnya, di Mahoney, skor diperbarui sesuai dengan hukum

$$

$$\ dot {\ hat {\ delta \ mathbf {\ omega}}} = k_ {b} \ mathbf {\ omega '}$$

Namun, hasilnya aneh: perkiraan mencapai 0,04 rad / s. Ketidakstabilan zero offset seperti itu tidak terjadi bahkan pada giroskop yang paling jahat sekalipun. Saya menduga masalahnya adalah bahwa Mahoney tidak menggunakan GNSS atau sensor eksternal lainnya - dan sepenuhnya dipengaruhi oleh pengaruh akselerasi. Hanya pada sumbu vertikal, di mana akselerasi tidak membahayakan, perkiraannya terlihat lebih atau kurang kuat:


Mahony et al., 2008

Akselerometer Beri Nilai Akselerometer Offset Nol $$$\ delta {\ mathbf {f}}$ jauh lebih sulit. Informasi tentang mereka harus diekstraksi dari kecepatan sudut kontrol yang sama $$$\ mathbf {\ omega '}$ . Namun, dalam gerakan bujursangkar, efek nol perpindahan akselerometer tidak dapat dibedakan dari kemiringan pembawa atau kecenderungan pemasangan blok sensor di atasnya. 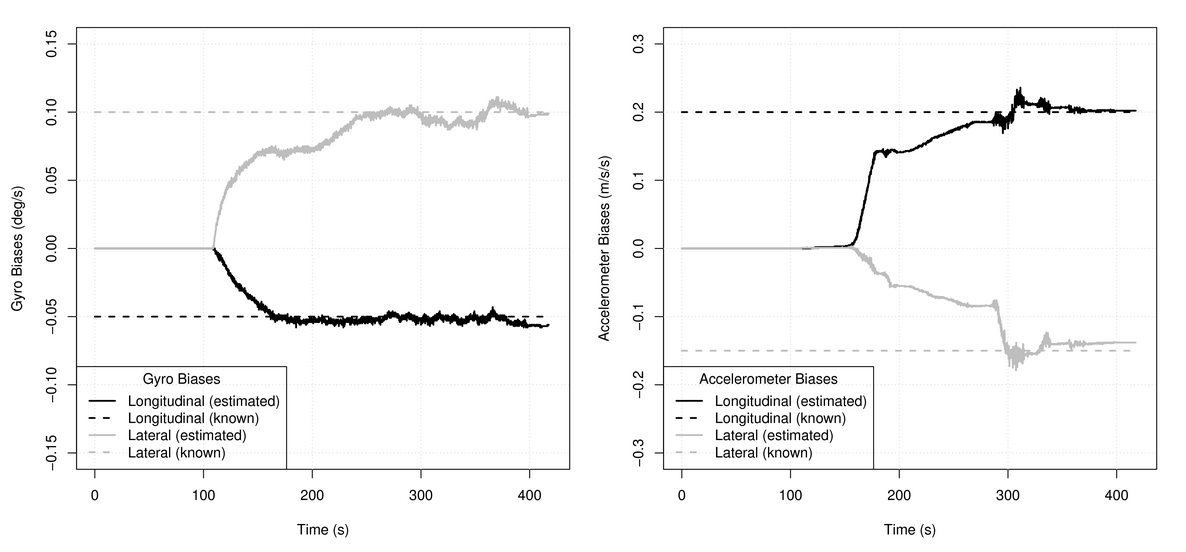Tidak ada tambahan untuk $$$\ mathbf {\ omega '}$ akselerometer tidak dibuat. Aditif hanya muncul pada gilirannya, yang memungkinkan kita untuk memisahkan dan secara independen mengevaluasi kesalahan giroskop dan akselerometer. Contoh bagaimana ini bisa dilakukan ada di artikel saya . Berikut foto-foto dari sana:

Alih-alih kesimpulan: bagaimana dengan filter Kalman?

Saya tidak ragu bahwa filter yang dijelaskan di sini hampir selalu memiliki keunggulan dibandingkan filter Kalman tradisional dalam hal kecepatan, kekompakan kode dan kemudahan pengaturan - untuk ini mereka diciptakan. Sedangkan untuk keakuratan penilaian, di sini semuanya tidak begitu jelas. Saya bertemu dengan filter Kalman yang dirancang dengan tidak berhasil, yang akurasinya jauh lebih rendah daripada filter dengan platform gyro virtual. Majwik juga membuktikan manfaat filternya sehubungan dengan beberapa perkiraan Kalman. Namun, untuk tugas estimasi orientasi yang sama, Anda dapat membangun setidaknya selusin rangkaian filter Kalman yang berbeda, dan masing-masing akan memiliki pengaturan yang tak terhitung jumlahnya. Saya tidak punya alasan untuk berpikir bahwa filter Mahoney atau Majwik akan lebih akurat daripada filter Kalman terbaik . Dan tentu saja, pendekatan Kalman akan selalu memiliki keunggulan universalitas: tidak menerapkan batasan ketat pada sifat dinamis spesifik dari sistem yang dievaluasi.