Geekly articles weekly

Kompresi data Huffman

Entri


Pada artikel ini saya akan berbicara tentang algoritma Huffman yang terkenal, serta penerapannya dalam kompresi data.

Sebagai hasilnya, kami akan menulis arsip sederhana. Sudah ada artikel tentang itu di Habré , tetapi tanpa implementasi praktis. Materi teoritis dari posting saat ini diambil dari pelajaran ilmu komputer sekolah dan buku Robert Lafore "Struktur Data dan Algoritma di Jawa". Jadi, semuanya ada di bawah jalan!

Sedikit pemikiran


Dalam file teks biasa, satu karakter dikodekan dengan 8 bit (ASCII encoding) atau 16 (Unicode encoding). Selanjutnya kami akan mempertimbangkan pengkodean ASCII. Misalnya, ambil baris s1 = "SUSIE MENGATAKAN ITU MUDAH \ n". Secara total, ada 22 karakter di baris, tentu saja, termasuk spasi dan karakter baris baru - '\ n'. File yang berisi baris ini akan berbobot 22 * ​​8 = 176 bit. Pertanyaan segera muncul: apakah rasional menggunakan semua 8 bit untuk mengkodekan 1 karakter? Kami tidak menggunakan semua karakter ASCII. Bahkan jika digunakan, akan lebih rasional untuk huruf yang paling sering - S - untuk memberikan kode sesingkat mungkin, dan untuk huruf paling langka - T (atau U, atau '\ n') - untuk memberikan kode yang lebih otentik. Ini adalah algoritma Huffman: Anda perlu menemukan opsi pengkodean terbaik, di mana file akan memiliki berat minimal. Sangat normal bahwa panjang kode akan berbeda untuk karakter yang berbeda - ini adalah dasar dari algoritma.

Coding


Mengapa tidak memberikan karakter 'S' kode, misalnya, panjang 1 bit: 0 atau 1. Biarkan 1. Maka kita akan memberikan karakter kedua yang paling ditemui - '' (spasi) - 0. Bayangkan, Anda mulai men-decode pesan Anda - string yang dikodekan s1 - dan Anda melihat bahwa kode dimulai dengan 1. Jadi apa yang harus dilakukan: apakah itu karakter S, atau apakah itu karakter lain, misalnya A? Oleh karena itu, aturan penting muncul:

Tidak ada kode yang harus merupakan awalan dari yang lain

Aturan ini adalah kunci dalam algoritma. Oleh karena itu, pembuatan kode dimulai dengan tabel frekuensi, yang menunjukkan frekuensi (jumlah kemunculan) dari masing-masing karakter:

Karakter dengan kejadian terbanyak harus dikodekan dengan jumlah bit sekecil mungkin . Saya akan memberikan contoh dari salah satu tabel kode yang mungkin:

Dengan demikian, pesan yang disandikan akan terlihat seperti ini:

10 01111 10 110 1111 00 10 010 1110 10 00 110 0110 00 110 10 00 1111 010 10 1110 01110

Saya memisahkan kode masing-masing karakter dengan spasi. Ini tidak akan benar-benar terjadi dalam file terkompresi!
Muncul pertanyaan: bagaimana cara salaga ini menghasilkan kode ? Bagaimana cara membuat tabel kode? Ini akan dibahas di bawah.

Membangun pohon huffman


Di sini pohon pencarian biner datang untuk menyelamatkan. Jangan khawatir, di sini metode pencarian, penyisipan, dan penghapusan tidak diperlukan. Berikut adalah struktur pohon di java:

 public class Node { private int frequence; private char letter; private Node leftChild; private Node rightChild; ... } 

 class BinaryTree { private Node root; public BinaryTree() { root = new Node(); } public BinaryTree(Node root) { this.root = root; } ... }

Ini bukan kode lengkap, kode lengkapnya ada di bawah.

Berikut adalah algoritma pembuatan pohon itu sendiri:

  1. Buat objek Node untuk setiap karakter dari pesan (baris s1). Dalam kasus kami, akan ada 9 node (objek Node). Setiap node terdiri dari dua bidang data: simbol dan frekuensi
  2. Buat objek Tree (BinaryTree) untuk masing-masing node Node. Node menjadi akar pohon.
  3. Rekatkan pohon ini dalam antrian prioritas. Semakin rendah frekuensinya, semakin tinggi prioritas. Jadi, ketika mengekstraksi, Dervo selalu dipilih dengan frekuensi terendah.

Selanjutnya, Anda perlu melakukan hal berikut secara siklis:

  1. Ekstrak dua pohon dari antrian prioritas dan buat mereka turunan dari simpul baru (simpul yang baru dibuat tanpa surat). Frekuensi simpul baru sama dengan jumlah frekuensi dua pohon turunan.
  2. Untuk simpul ini, buat pohon dengan root di simpul ini. Rekatkan pohon ini kembali ke antrian prioritas. (Karena pohon memiliki frekuensi baru, maka kemungkinan besar pohon itu akan sampai ke tempat baru dalam antrian)
  3. Lanjutkan langkah 1 dan 2 hingga hanya ada satu pohon yang tersisa dalam antrian - pohon Huffman

Pertimbangkan algoritma ini pada baris s1:



Di sini, simbol "Jika" (linefeed) menunjukkan transisi ke baris baru, "sp" (spasi) adalah spasi.

Apa selanjutnya


Kami punya pohon Huffman. Baiklah Dan apa hubungannya dengan itu? Mereka tidak akan mengambilnya secara gratis. Dan kemudian, Anda perlu melacak semua jalur yang mungkin dari akar ke daun pohon. Mari kita sepakat untuk menetapkan tepi 0 jika mengarah ke keturunan kiri dan 1 jika ke kanan. Sebenarnya, dalam notasi ini, kode simbol adalah jalur dari akar pohon ke lembar yang berisi simbol yang sama ini.



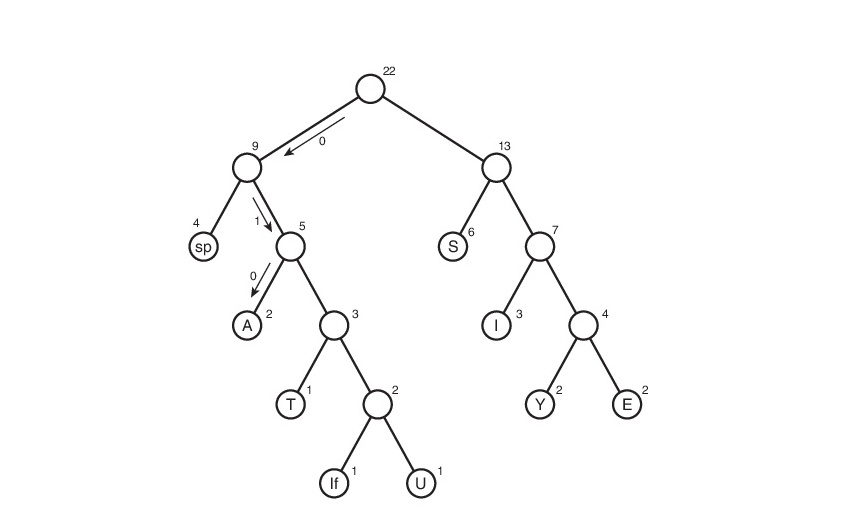
Jadi, tabel kode ternyata. Perhatikan bahwa jika kita mempertimbangkan tabel ini, kita dapat menyimpulkan tentang "bobot" dari setiap karakter - ini adalah panjang kodenya. Maka file yang dikompresi akan menimbang: 2 * 3 + 2 * 4 + 3 * 3 + 6 * 2 + 1 * 4 + 1 * 5 + 2 * 4 + 4 * 2 + 1 * 5 = 65 bit. Awalnya, beratnya 176 bit. Karenanya, kami menguranginya sebanyak 176/65 = 2,7 kali! Tapi ini utopia. Koefisien semacam itu tidak mungkin diperoleh. Mengapa Ini akan dibahas sedikit kemudian.

Decoding


Yah, mungkin hal paling sederhana yang tersisa adalah decoding. Saya pikir banyak dari Anda menduga bahwa tidak mungkin hanya membuat file terkompresi tanpa petunjuk bagaimana itu dikodekan - kami tidak akan dapat men-decode itu! Ya, sulit bagi saya untuk menyadari hal ini, tetapi saya harus membuat file teks table.txt dengan tabel kompresi:

 01110 00 A010 E1111 I110 S10 T0110 U01111 Y1110

Rekam tabel dalam bentuk 'karakter' "kode karakter". Mengapa 01110 tanpa karakter? Bahkan, itu dengan simbol, hanya alat java yang digunakan oleh saya ketika mengeluarkan ke file, karakter baris baru - '\ n' - dikonversi ke baris baru (tidak peduli seberapa bodoh kedengarannya). Oleh karena itu, baris kosong di atas adalah karakter untuk kode 01110. Untuk kode 00, karakter adalah spasi di awal baris. Saya harus segera mengatakan bahwa metode kami menyimpan tabel ini mungkin mengklaim yang paling tidak rasional. Tetapi sederhana untuk dipahami dan diimplementasikan. Saya akan senang mendengar rekomendasi Anda di komentar mengenai optimasi.

Memiliki tabel ini sangat mudah untuk diterjemahkan. Ingat aturan apa yang dipandu oleh kami saat membuat pengodean:

Tidak ada kode yang harus diawali kode lain

Di sinilah ia memainkan peran fasilitasi. Kami membaca berurutan sedikit demi sedikit dan, segera setelah string yang diterima d, yang terdiri dari bit yang dibaca, cocok dengan pengkodean yang sesuai dengan karakter karakter, kami segera tahu bahwa karakter karakter telah dikodekan (dan hanya itu!). Selanjutnya, kita menulis karakter di baris decoding (baris yang berisi pesan yang didekodekan), nol baris d, dan kemudian membaca file yang disandikan.

Implementasi


Saatnya mempermalukan kode saya dengan menulis arsip. Sebut saja Kompresor.

Mari kita mulai dari awal. Pertama, kita menulis kelas Node:

 public class Node { private int frequence;// private char letter;// private Node leftChild;//  private Node rightChild;//  public Node(char letter, int frequence) { //,  this.letter = letter; this.frequence = frequence; } public Node() {}//    (.       ) public void addChild(Node newNode) {//  if (leftChild == null)//  =>  =>    leftChild = newNode; else { if (leftChild.getFrequence() <= newNode.getFrequence()) // ,   rightChild = newNode;// ,     else { rightChild = leftChild; leftChild = newNode; } } frequence += newNode.getFrequence();//  } public Node getLeftChild() { return leftChild; } public Node getRightChild() { return rightChild; } public int getFrequence() { return frequence; } public char getLetter() { return letter; } public boolean isLeaf() {//   return leftChild == null && rightChild == null; } }

Sekarang pohonnya:

 class BinaryTree { private Node root; public BinaryTree() { root = new Node(); } public BinaryTree(Node root) { this.root = root; } public int getFrequence() { return root.getFrequence(); } public Node getRoot() { return root; } }

Antrian Prioritas:

 import java.util.ArrayList;//-,      class PriorityQueue { private ArrayList<BinaryTree> data;//  private int nElems;//-    public PriorityQueue() { data = new ArrayList<BinaryTree>(); nElems = 0; } public void insert(BinaryTree newTree) {// if (nElems == 0) data.add(newTree); else { for (int i = 0; i < nElems; i++) { if (data.get(i).getFrequence() > newTree.getFrequence()) {//     data.add(i, newTree);// . ,  c       1  break;//       } if (i == nElems - 1) data.add(newTree); } } nElems++;// -   1 } public BinaryTree remove() {//   BinaryTree tmp = data.get(0);//   data.remove(0);//,  nElems--;// -   1 return tmp;//  (   ) } }

Kelas yang menciptakan pohon Huffman:

 public class HuffmanTree { private final byte ENCODING_TABLE_SIZE = 127;//   private String myString;// private BinaryTree huffmanTree;//  private int[] freqArray;//  private String[] encodingArray;//  //----------------constructor---------------------- public HuffmanTree(String newString) { myString = newString; freqArray = new int[ENCODING_TABLE_SIZE]; fillFrequenceArray(); huffmanTree = getHuffmanTree(); encodingArray = new String[ENCODING_TABLE_SIZE]; fillEncodingArray(huffmanTree.getRoot(), "", ""); } //--------------------frequence array------------------------ private void fillFrequenceArray() { for (int i = 0; i < myString.length(); i++) { freqArray[(int)myString.charAt(i)]++; } } public int[] getFrequenceArray() { return freqArray; } //------------------------huffman tree creation------------------ private BinaryTree getHuffmanTree() { PriorityQueue pq = new PriorityQueue(); //   for (int i = 0; i < ENCODING_TABLE_SIZE; i++) { if (freqArray[i] != 0) {//     Node newNode = new Node((char) i, freqArray[i]);//    Node BinaryTree newTree = new BinaryTree(newNode);//  Node  BinaryTree pq.insert(newTree);//   } } while (true) { BinaryTree tree1 = pq.remove();//    . try { BinaryTree tree2 = pq.remove();//     Node newNode = new Node();//  Node newNode.addChild(tree1.getRoot());//      newNode.addChild(tree2.getRoot()); pq.insert(new BinaryTree(newNode); } catch (IndexOutOfBoundsException e) {//     return tree1; } } } public BinaryTree getTree() { return huffmanTree; } //-------------------encoding array------------------ void fillEncodingArray(Node node, String codeBefore, String direction) {//   if (node.isLeaf()) { encodingArray[(int)node.getLetter()] = codeBefore + direction; } else { fillEncodingArray(node.getLeftChild(), codeBefore + direction, "0"); fillEncodingArray(node.getRightChild(), codeBefore + direction, "1"); } } String[] getEncodingArray() { return encodingArray; } public void displayEncodingArray() {//  fillEncodingArray(huffmanTree.getRoot(), "", ""); System.out.println("======================Encoding table===================="); for (int i = 0; i < ENCODING_TABLE_SIZE; i++) { if (freqArray[i] != 0) { System.out.print((char)i + " "); System.out.println(encodingArray[i]); } } System.out.println("========================================================"); } //----------------------------------------------------- String getOriginalString() { return myString; } }

Kelas yang mengandung encode / decode:

 public class HuffmanOperator { private final byte ENCODING_TABLE_SIZE = 127;//  private HuffmanTree mainHuffmanTree;//  (   ) private String myString;//  private int[] freqArray;//  private String[] encodingArray;//  private double ratio;//  public HuffmanOperator(HuffmanTree MainHuffmanTree) {//for compress this.mainHuffmanTree = MainHuffmanTree; myString = mainHuffmanTree.getOriginalString(); encodingArray = mainHuffmanTree.getEncodingArray(); freqArray = mainHuffmanTree.getFrequenceArray(); } public HuffmanOperator() {}//for extract; //---------------------------------------compression----------------------------------------------------------- private String getCompressedString() { String compressed = ""; String intermidiate = "";// (  ) //System.out.println("=============================Compression======================="); //displayEncodingArray(); for (int i = 0; i < myString.length(); i++) { intermidiate += encodingArray[myString.charAt(i)]; } //      .       8=> //    ( 1,  ) byte counter = 0;//     (   : 0<=counter<8<127) for (int length = intermidiate.length(), delta = 8 - length % 8; counter < delta ; counter++) {//delta -    intermidiate += "0"; } // -         compressed = String.format("%8s", Integer.toBinaryString(counter & 0xff)).replace(" ", "0") + intermidiate; //  setCompressionRatio(); //System.out.println("==============================================================="); return compressed; } private void setCompressionRatio() {//   double sumA = 0, sumB = 0;//A-the original sum for (int i = 0; i < ENCODING_TABLE_SIZE; i++) { if (freqArray[i] != 0) { sumA += 8 * freqArray[i]; sumB += encodingArray[i].length() * freqArray[i]; } } ratio = sumA / sumB; } public byte[] getBytedMsg() {//final compression StringBuilder compressedString = new StringBuilder(getCompressedString()); byte[] compressedBytes = new byte[compressedString.length() / 8]; for (int i = 0; i < compressedBytes.length; i++) { compressedBytes[i] = (byte) Integer.parseInt(compressedString.substring(i * 8, (i + 1) * 8), 2); } return compressedBytes; } //---------------------------------------end of compression---------------------------------------------------------------- //------------------------------------------------------------extract----------------------------------------------------- public String extract(String compressed, String[] newEncodingArray) { String decompressed = ""; String current = ""; String delta = ""; encodingArray = newEncodingArray; //displayEncodingArray(); // -   for (int i = 0; i < 8; i++) delta += compressed.charAt(i); int ADDED_ZEROES = Integer.parseInt(delta, 2); for (int i = 8, l = compressed.length() - ADDED_ZEROES; i < l; i++) { //i = 8, ..      -   current += compressed.charAt(i); for (int j = 0; j < ENCODING_TABLE_SIZE; j++) { if (current.equals(encodingArray[j])) {//  decompressed += (char)j;//   current = "";//    } } } return decompressed; } public String getEncodingTable() { String enc = ""; for (int i = 0; i < encodingArray.length; i++) { if (freqArray[i] != 0) enc += (char)i + encodingArray[i] + '\n'; } return enc; } public double getCompressionRatio() { return ratio; } public void displayEncodingArray() {//  System.out.println("======================Encoding table===================="); for (int i = 0; i < ENCODING_TABLE_SIZE; i++) { //if (freqArray[i] != 0) { System.out.print((char)i + " "); System.out.println(encodingArray[i]); //} } System.out.println("========================================================"); } }

Kelas yang memfasilitasi penulisan ke file:

 import java.io.File; import java.io.PrintWriter; import java.io.FileNotFoundException; import java.io.FileOutputStream; import java.io.IOException; import java.io.Closeable; public class FileOutputHelper implements Closeable { private File outputFile; private FileOutputStream fileOutputStream; public FileOutputHelper(File file) throws FileNotFoundException { outputFile = file; fileOutputStream = new FileOutputStream(outputFile); } public void writeByte(byte msg) throws IOException { fileOutputStream.write(msg); } public void writeBytes(byte[] msg) throws IOException { fileOutputStream.write(msg); } public void writeString(String msg) { try (PrintWriter pw = new PrintWriter(outputFile)) { pw.write(msg); } catch (FileNotFoundException e) { System.out.println(" ,     !"); } } @Override public void close() throws IOException { fileOutputStream.close(); } public void finalize() throws IOException { close(); } }

Kelas yang memfasilitasi membaca dari file:

 import java.io.FileInputStream; import java.io.EOFException; import java.io.BufferedReader; import java.io.InputStreamReader; import java.io.Closeable; import java.io.File; import java.io.IOException; public class FileInputHelper implements Closeable { private FileInputStream fileInputStream; private BufferedReader fileBufferedReader; public FileInputHelper(File file) throws IOException { fileInputStream = new FileInputStream(file); fileBufferedReader = new BufferedReader(new InputStreamReader(fileInputStream)); } public byte readByte() throws IOException { int cur = fileInputStream.read(); if (cur == -1)//   throw new EOFException(); return (byte)cur; } public String readLine() throws IOException { return fileBufferedReader.readLine(); } @Override public void close() throws IOException{ fileInputStream.close(); } }

Nah, dan kelas utama:

 import java.io.File; import java.nio.charset.MalformedInputException; import java.io.FileNotFoundException; import java.io.IOException; import java.nio.file.Files; import java.nio.file.NoSuchFileException; import java.nio.file.Paths; import java.util.List; import java.io.EOFException; public class Main { private static final byte ENCODING_TABLE_SIZE = 127; public static void main(String[] args) throws IOException { try {//       if (args[0].equals("--compress") || args[0].equals("-c")) compress(args[1]); else if ((args[0].equals("--extract") || args[0].equals("-x")) && (args[2].equals("--table") || args[2].equals("-t"))) { extract(args[1], args[3]); } else throw new IllegalArgumentException(); } catch (ArrayIndexOutOfBoundsException | IllegalArgumentException e) { System.out.println("    "); System.out.println(" Readme.txt"); e.printStackTrace(); } } public static void compress(String stringPath) throws IOException { List<String> stringList; File inputFile = new File(stringPath); String s = ""; File compressedFile, table; try { stringList = Files.readAllLines(Paths.get(inputFile.getAbsolutePath())); } catch (NoSuchFileException e) { System.out.println(" ,     !"); return; } catch (MalformedInputException e) { System.out.println("    "); return; } for (String item : stringList) { s += item; s += '\n'; } HuffmanOperator operator = new HuffmanOperator(new HuffmanTree(s)); compressedFile = new File(inputFile.getAbsolutePath() + ".cpr"); compressedFile.createNewFile(); try (FileOutputHelper fo = new FileOutputHelper(compressedFile)) { fo.writeBytes(operator.getBytedMsg()); } //create file with encoding table: table = new File(inputFile.getAbsolutePath() + ".table.txt"); table.createNewFile(); try (FileOutputHelper fo = new FileOutputHelper(table)) { fo.writeString(operator.getEncodingTable()); } System.out.println("   : " + compressedFile.getAbsolutePath()); System.out.println("    " + table.getAbsolutePath()); System.out.println("     !"); double idealRatio = Math.round(operator.getCompressionRatio() * 100) / (double) 100;//  double realRatio = Math.round((double) inputFile.length() / ((double) compressedFile.length() + (double) table.length()) * 100) / (double)100;//  System.out.println("    " + idealRatio); System.out.println("      " + realRatio); } public static void extract(String filePath, String tablePath) throws FileNotFoundException, IOException { HuffmanOperator operator = new HuffmanOperator(); File compressedFile = new File(filePath), tableFile = new File(tablePath), extractedFile = new File(filePath + ".xtr"); String compressed = ""; String[] encodingArray = new String[ENCODING_TABLE_SIZE]; //read compressed file //!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!check here: try (FileInputHelper fi = new FileInputHelper(compressedFile)) { byte b; while (true) { b = fi.readByte();//method returns EOFException compressed += String.format("%8s", Integer.toBinaryString(b & 0xff)).replace(" ", "0"); } } catch (EOFException e) { } //-------------------- //read encoding table: try (FileInputHelper fi = new FileInputHelper(tableFile)) { fi.readLine();//skip first empty string encodingArray[(byte)'\n'] = fi.readLine();//read code for '\n' while (true) { String s = fi.readLine(); if (s == null) throw new EOFException(); encodingArray[(byte)s.charAt(0)] = s.substring(1, s.length()); } } catch (EOFException ignore) {} extractedFile.createNewFile(); //extract: try (FileOutputHelper fo = new FileOutputHelper(extractedFile)) { fo.writeString(operator.extract(compressed, encodingArray)); } System.out.println("    " + extractedFile.getAbsolutePath()); } }

File instruksi readme.txt terserah Anda untuk menulis sendiri :-)

Kesimpulan


Mungkin ini yang ingin saya katakan. Jika Anda memiliki sesuatu untuk dikatakan tentang ketidakmampuan saya untuk perbaikan dalam kode, algoritma, dan optimasi apa pun secara umum, jangan ragu untuk menulis. Jika saya salah paham sesuatu, juga menulis. Saya akan senang mendengar dari Anda di komentar!

PS


Ya, ya, saya masih di sini, karena saya tidak lupa tentang koefisien. Untuk baris s1, tabel penyandian memiliki berat 48 byte - jauh lebih banyak daripada file asli, dan mereka tidak melupakan nol tambahan (jumlah nol yang ditambahkan adalah 7) => rasio kompresi akan kurang dari satu: 176 / (65 + 48 * 8 + 7) = 0,38. Jika Anda juga memperhatikan ini, maka tidak hanya di wajah Anda sudah selesai. Ya, implementasi ini akan sangat tidak efisien untuk file kecil. Tetapi apa yang terjadi pada file besar? Ukuran file jauh melebihi ukuran tabel penyandian. Di sini algoritma berfungsi sebagaimana mestinya! Sebagai contoh, untuk monolog Faust, pengarsipan memberikan koefisien nyata (tidak ideal) sama dengan 1,46 - hampir satu setengah kali! Dan ya, file itu seharusnya dalam bahasa Inggris.

Source: https://habr.com/ru/post/id438512/

More articles:


All Articles