Menulis XGBoost dari awal - bagian 1: pohon keputusan

Halo, Habr!

Setelah banyak mencari panduan berkualitas tinggi tentang pohon keputusan dan algoritma ensemble (boosting, decision forest, dll.) Dengan implementasi langsung mereka dalam bahasa pemrograman, dan tanpa menemukan apa pun (siapa pun yang menemukan - tulis di komentar, mungkin saya akan belajar sesuatu yang baru), Saya memutuskan untuk membuat kepemimpinan saya sendiri, karena saya ingin melihatnya. Tugas dalam kata-kata itu sederhana, tetapi, seperti yang Anda tahu, iblis ada dalam hal-hal kecil, di mana ada banyak algoritma dengan pohon.

Karena topiknya cukup luas, akan sangat sulit untuk memasukkan semuanya ke dalam satu artikel, sehingga akan ada dua publikasi: yang pertama dikhususkan untuk pohon, dan bagian kedua akan dikhususkan untuk implementasi algoritma peningkatan gradien. Semua materi yang disajikan di sini disusun dan dirancang berdasarkan sumber terbuka, kode saya, kode kolega dan teman. Saya memperingatkan Anda segera, akan ada banyak kode.



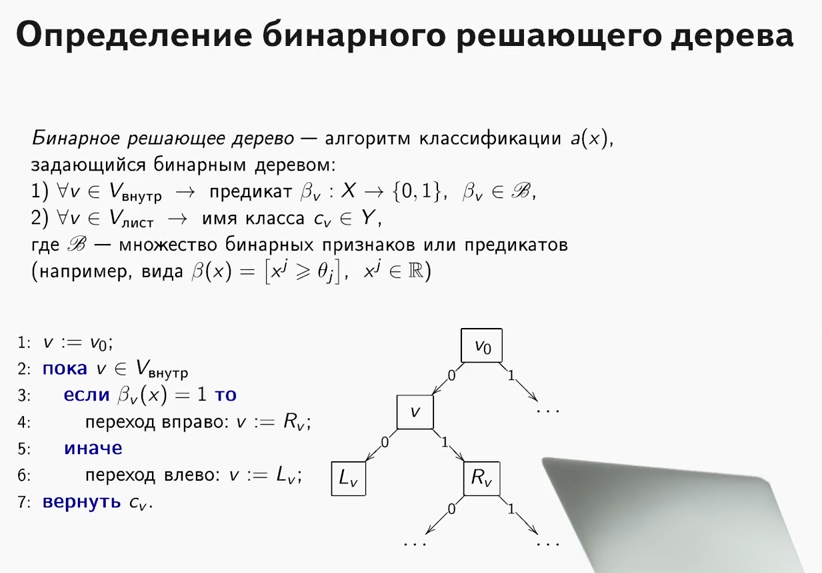
Jadi apa yang perlu Anda ketahui dan dapat belajar bagaimana menulis algoritma ensemble Anda sendiri dengan pohon keputusan dari awal? Karena ensemble algoritme tidak lebih dari komposisi "algoritme lemah", menulis ensembel yang baik membutuhkan "algoritme lemah" yang baik, kami akan menganalisisnya secara terperinci dalam artikel ini. Seperti namanya, ini adalah pohon yang penting, dan bergerak dari yang sederhana ke yang kompleks, kita akan belajar bagaimana menulisnya. Dalam hal ini, penekanan akan ditempatkan langsung pada implementasi, keseluruhan teori akan disajikan dalam minimum, pada dasarnya saya akan memberikan tautan ke materi untuk studi independen.

Untuk mempelajari materi, Anda perlu memahami seberapa baik atau buruk algoritma kami. Kami akan memahami dengan sangat sederhana - kami akan memperbaiki beberapa set data tertentu dan kami akan membandingkan algoritma kami dengan algoritma pohon dari Sklearn (well, apa yang akan terjadi tanpa perpustakaan ini). Kami akan membandingkan banyak hal: kompleksitas algoritme, metrik data, waktu aktif, dll.

Apa itu pohon yang menentukan? Bahan yang sangat bagus, yang menjelaskan prinsip pohon keputusan, terkandung dalam kursus ODS (omong-omong, kursus keren, saya merekomendasikannya kepada mereka yang memulai perkenalan mereka dengan ML).

Penjelasan yang sangat penting: dalam semua kasus yang dijelaskan di bawah ini, semua tanda akan nyata, kami tidak akan melakukan transformasi khusus dengan data di luar algoritme (kami membandingkan algoritme, bukan kumpulan data).

Sekarang mari kita belajar bagaimana menyelesaikan masalah regresi menggunakan pohon keputusan. Kami akan menggunakan metrik MSE sebagai entropi.

Kami menerapkan kelas RegressionTree sangat sederhana, yang didasarkan pada pendekatan rekursif. Secara sengaja, kita mulai dengan implementasi yang sangat tidak efektif, tetapi mudah untuk memahami kelas tersebut agar dapat meningkatkannya di masa depan.

1. kelas RegressionTree ()

 class RegressionTree(): '''  RegressionTree   .    ,      . ''' def __init__(self, max_depth=3, n_epoch=10, min_size=8): '''   . ''' self.max_depth = max_depth #   self.min_size = min_size #    self.value = 0 #    (   ) self.feature_idx = -1 #    self.feature_threshold = 0 #    self.left = None #   self.right = None #   def fit(self, X, y): '''   .     . ''' #    self.value = y.mean() base_error = ((y - self.value) ** 2).sum() error = base_error flag = 0 #       prev_error_left = base_error prev_error_right = 0 #     0 -  if self.max_depth <= 1: return dim_shape = X.shape[1] #       left_value = 0 right_value = 0 #     for feat in range(dim_shape): #   idxs = np.argsort(X[:, feat]) #        N = X.shape[0] N1, N2 = N, 0 thres = 1 #      while thres < N - 1: N1 -= 1 N2 += 1 idx = idxs[thres] x = X[idx, feat] #    if thres < N - 1 and x == X[idxs[thres + 1], feat]: thres += 1 continue # ,         target_right = y[idxs][:thres] target_left = y[idxs][thres:] mean_right = y[idxs][:thres].mean(), mean_left = y[idxs][thres:].mean() #        - #   (  ) left_shape = target_left.shape[0] right_shape = target_right.shape[0] mean_left_array = [mean_left for _ in range(left_shape)] mean_right_array = [mean_right for _ in range(right_shape)] #      prev_error_left = N1/N * mse(target_left, mean_left_array) prev_error_right = N2/N * mse(target_right, mean_right_array) #    ,   if (prev_error_left + prev_error_right < error): if (min(N1,N2) > self.min_size): self.feature_idx = feat self.feature_threshold = x left_value = mean_left right_value = mean_right flag = 1 error = prev_error_left + prev_error_right thres += 1 #     ,  if self.feature_idx == -1: return #   -   ,    #   -     self.left = RegressionTree(self.max_depth - 1) self.left.value = left_value self.right = RegressionTree(self.max_depth - 1) self.right.value = right_value #   idxs_l = (X[:, self.feature_idx] > self.feature_threshold) idxs_r = (X[:, self.feature_idx] <= self.feature_threshold) #  self.left.fit(X[idxs_l, :], y[idxs_l]) self.right.fit(X[idxs_r, :], y[idxs_r]) def __predict(self, x): '''     -  ,         self.value -    . ''' if self.feature_idx == -1: return self.value if x[self.feature_idx] > self.feature_threshold: return self.left.__predict(x) else: return self.right.__predict(x) def predict(self, X): '''    -      __predict(). ''' y = np.zeros(X.shape[0]) for i in range(X.shape[0]): y[i] = self.__predict(X[i]) return y 

Saya akan menjelaskan secara singkat apa yang dilakukan masing-masing metode di sini.

Metode fit , sesuai namanya, mengajarkan model. Sampel pelatihan diterapkan pada input dan prosedur pelatihan pohon dilakukan. Mengurutkan tanda-tanda, kami mencari partisi pohon terbaik dalam hal mengurangi entropi, dalam hal ini mse . Untuk menentukan bahwa itu mungkin untuk menemukan perpecahan yang baik adalah sangat sederhana, itu sudah cukup untuk memenuhi dua syarat. Kami tidak ingin beberapa objek jatuh ke partisi (perlindungan terhadap pelatihan ulang), dan kesalahan rata-rata untuk mse harus lebih kecil daripada kesalahan yang sekarang ada di pohon - kami mencari keuntungan yang sama dalam perolehan informasi . Setelah melalui semua tanda dan semua nilai unik sedemikian rupa, kita akan melalui semua opsi dan memilih partisi terbaik. Dan kemudian kami melakukan panggilan rekursif pada partisi yang diterima sampai kondisi untuk keluar rekursi terpenuhi.

Metode __predict , seperti namanya, membuat predikat. Setelah menerima objek sebagai input, ia akan melewati node-node dari pohon yang dihasilkan - di setiap node nomor atribut dan nilai ditetapkan padanya, dan tergantung pada nilai apa yang digunakan metode masuk objek untuk atribut ini, kita pergi ke turunan kanan atau ke kiri, sampai kita sampai pada lembar, di mana akan ada jawaban untuk objek ini.

Metode predict melakukan hal yang sama dengan metode sebelumnya, hanya untuk sekelompok objek.

Kami mengimpor kumpulan data rumah California yang terkenal. Ini adalah dataset reguler dengan data dan target untuk menyelesaikan masalah regresi.

 data = datasets.fetch_california_housing() X = np.array(data.data) y = np.array(data.target) 

Baiklah, mari kita mulai perbandingan! Pertama, mari kita lihat seberapa cepat algoritma belajar. Kami menetapkan di Sklearn dan kami satu-satunya parameter max_depth , biarkan sama dengan 2.

 %%time A = RegressionTree(2) #    A.fit(X,y) 

 from sklearn.tree import DecisionTreeRegressor %%time model = DecisionTreeRegressor(max_depth=2) #  Sklearn model.fit(X,y) 

Berikut ini akan ditampilkan:

• Untuk algoritma kami - waktu CPU: pengguna 4 menit 47, sistem: 8,25 ms, total: 4 menit 47s
  Waktu dinding: 4 menit 47-an
• Untuk Sklearn - waktu CPU: pengguna 53,5 ms, sys: 0 ns, total: 53,5 ms
  Waktu dinding: 53,4 ms

Seperti yang Anda lihat, algoritme belajar ribuan kali lebih lambat. Apa alasannya Mari kita perbaiki.

Ingat bagaimana prosedur untuk menemukan partisi terbaik diatur. Seperti yang Anda tahu, dalam kasus umum, dengan ukuran objek $$$N$ dan dengan jumlah tanda $$$d$ , kesulitan menemukan split terbaik adalah $$$O (N * logN * d)$ .

Dari mana datangnya kompleksitas ini?

Pertama, untuk menghitung ulang kesalahan secara efektif, perlu menyortir semua kolom untuk pindah dari yang terkecil ke yang terbesar sebelum melewati atribut. Saat kami melakukan ini untuk setiap sifat, ini menciptakan kompleksitas yang sesuai. Seperti yang Anda lihat, kami mengurutkan tanda-tanda, tetapi masalahnya terletak pada menghitung ulang kesalahan - setiap kali kami mengarahkan data ke metode mse , yang bekerja untuk baris. Ini membuat kesalahan penghitungan ulang jadi tidak efisien! Setelah semua, maka kesulitan menemukan perpecahan meningkat menjadi $$$O (N ^ 2 * d)$ untuk yang besar $$$N$ sangat memperlambat algoritma. Karena itu, kami melanjutkan dengan lancar ke item berikutnya.

2. Kelas RegressionTree () dengan penghitungan kesalahan cepat

Apa yang perlu dilakukan untuk dengan cepat menceritakan kesalahan? Ambil pena dan kertas, dan cat bagaimana kita harus mengubah formula.

Misalkan pada beberapa langkah sudah ada kesalahan dihitung $$$N$ benda. Ini memiliki rumus berikut: $$$\ sum_ {i = 1} ^ n (y_i - \ frac {\ sum_ {i = 1} ^ N y_i} {N}) ^ 2$ . Di sini perlu untuk membagi dengan $$$N$ tetapi untuk sekarang mari kita hilangkan itu. Kami ingin cepat mendapatkan kesalahan ini - $$$\ sum_ {i = 1} ^ {N-1} (y_i - \ frac {\ sum_ {i = 1} ^ {N-1} y_i} {N-1}) ^ 2$ , yaitu, membuang kesalahan yang elemen perkenalkan $$$y_i$ ke bagian lain.

Karena kita melempar objek, kesalahan harus diceritakan di dua tempat - di sisi kanan (tidak termasuk objek ini) dan di sisi kiri (memperhitungkan objek ini). Tetapi tanpa kehilangan keumuman kami akan menyimpulkan hanya satu formula, karena mereka akan serupa.

Karena kami bekerja dengan mse , kami kurang beruntung: agak sulit untuk mendapatkan penghitungan ulang kesalahan yang cepat, tetapi ketika bekerja dengan metrik lain (misalnya, kriteria Gini, jika kami menyelesaikan masalah klasifikasi), penghitungan ulang cepat jauh lebih mudah.

Baiklah, mari kita mulai membuat formula!

$$

$$\ sum_ {i = 1} ^ N (y_i - \ frac {\ sum_ {i = 1} ^ N y_i} {N}) ^ 2 = \ sum_ {i = 1} ^ {N-1} (y_i - \ frac {\ sum_ {i = 1} ^ N y_i} {N}) ^ 2 + (y_N - \ frac {\ sum_ {i = 1} ^ N y_i} {N}) ^ 2$$

Kami akan menulis anggota pertama:

$$

$$\ sum_ {i = 1} ^ {N-1} (y_i - \ frac {\ sum_ {i = 1} ^ N y_i} {N}) ^ 2 = \ sum_ {i = 1} ^ {N-1 } (y_i - \ frac {\ sum_ {i = 1} ^ {N-1} y_i + y_N} {N}) ^ 2 = \\ \ sum_ {i = 1} ^ {N-1} (\ frac { Ny_i - \ sum_ {i = 1} ^ {N-1} y_i} {N} - \ frac {y_N} {N}) ^ 2 = \\ \ sum_ {i = 1} ^ {N-1} (\ frac {(N-1) y_i - \ sum_ {i = 1} ^ {N-1} y_i} {N} - \ frac {y_N - y_i} {N}) ^ 2 = \\ \ sum_ {i = 1 } ^ {N-1} (\ frac {(N-1) y_i - \ sum_ {i = 1} ^ {N-1} y_i} {N}) ^ 2 - 2 (\ frac {(N-1) y_i - \ sum_ {i = 1} ^ {N-1} y_i} {N}) \ frac {y_N - y_i} {N} + (\ frac {y_N - y_i} {N}) ^ 2 = \\ \ sum_ {i = 1} ^ {N-1} (\ frac {(N-1) y_i - \ sum_ {i = 1} ^ {N-1} y_i} {N}) ^ 2 - \ sum_ {i = 1} ^ {N-1} (2 (\ frac {(N-1) y_i - \ sum_ {i = 1} ^ {N-1} y_i} {N}) \ frac {y_N - y_i} {N} - (\ frac {y_N - y_i} {N}) ^ 2) = \\ \ sum_ {i = 1} ^ {N-1} (\ frac {(N-1) y_i - \ sum_ {i = 1} ^ {N-1} y_i} {N-1}) ^ 2 * (\ frac {N-1} {N}) ^ 2 - \ sum_ {i = 1} ^ {N-1} (2 (\ frac {(N-1) y_i - \ sum_ {i = 1} ^ {N-1} y_i} {N}) \ frac {y_N - y_i} {N} - \\ - (\ frac {y_N - y_i} { N}) ^ 2)$$

Ugh, hanya tersisa sedikit. Tetap hanya untuk menyatakan jumlah yang diperlukan.

$$

$$\ sum_ {i = 1} ^ {N} (y_i - \ frac {\ sum_ {i = 1} ^ {N} y_i} {N}) ^ 2 = \ sum_ {i = 1} ^ {N-1 } (\ frac {(N-1) y_i - \ sum_ {i = 1} ^ {N-1} y_i} {N-1}) ^ 2 * (\ frac {N-1} {N}) ^ 2 - \\ \ sum_ {i = 1} ^ {N-1} (2 (\ frac {(N-1) y_i - \ sum_ {i = 1} ^ {N-1} y_i} {N}) (\ frac {y_N - y_i} {N}) - (\ frac {y_N - y_i} {N}) ^ 2) + (y_N - \ sum_ {i = 1} ^ {N} \ frac {y_i} {N}) ^ 2$$

Dan kemudian jelas bagaimana mengekspresikan jumlah yang diinginkan. Untuk menghitung ulang kesalahan, kita hanya perlu menyimpan jumlah elemen di kanan dan kiri, serta elemen baru itu sendiri, yang sampai pada input. Sekarang kesalahan dihitung ulang untuk $$$O (1)$ .

Baiklah, mari kita terapkan ini dalam kode.

 class RegressionTreeFastMse(): '''  RegressionTree    .        O(1). ''' #    def __init__(self, max_depth=3, min_size=10): self.max_depth = max_depth self.min_size = min_size self.value = 0 self.feature_idx = -1 self.feature_threshold = 0 self.left = None self.right = None #   -     def fit(self, X, y): #   -   y self.value = y.mean() #   - mse     (  # ,     )   base_error = ((y - self.value) ** 2).sum() error = base_error flag = 0 #     if self.max_depth <= 1: return dim_shape = X.shape[1] left_value, right_value = 0, 0 for feat in range(dim_shape): prev_error1, prev_error2 = base_error, 0 idxs = np.argsort(X[:, feat]) #      mean1, mean2 = y.mean(), 0 sm1, sm2 = y.sum(), 0 N = X.shape[0] N1, N2 = N, 0 thres = 1 while thres < N - 1: N1 -= 1 N2 += 1 idx = idxs[thres] x = X[idx, feat] #   -        delta1 = (sm1 - y[idx]) * 1.0 / N1 - mean1 delta2 = (sm2 + y[idx]) * 1.0 / N2 - mean2 #   sm1 -= y[idx] sm2 += y[idx] #    O(1) prev_error1 += (delta1**2) * N1 prev_error1 -= (y[idx] - mean1)**2 prev_error1 -= 2 * delta1 * (sm1 - mean1 * N1) mean1 = sm1/N1 prev_error2 += (delta2**2) * N2 prev_error2 += (y[idx] - mean2)**2 prev_error2 -= 2 * delta2 * (sm2 - mean2 * N2) mean2 = sm2/N2 #       if thres < N - 1 and np.abs(x - X[idxs[thres + 1], feat]) < 1e-5: thres += 1 continue # 2 ,    -   #   - -    if (prev_error1 + prev_error2 < error): if (min(N1,N2) > self.min_size): #         self.feature_idx, self.feature_threshold = feat, x #     left_value, right_value = mean1, mean2 #  -     flag = 1 error = prev_error1 + prev_error2 thres += 1 #   ,  if self.feature_idx == -1: return self.left = RegressionTreeFastMse(self.max_depth - 1) # print ("    %d"%(self.max_depth - 1)) self.left.value = left_value self.right = RegressionTreeFastMse(self.max_depth - 1) # print ("    %d"%(self.max_depth - 1)) self.right.value = right_value idxs_l = (X[:, self.feature_idx] > self.feature_threshold) idxs_r = (X[:, self.feature_idx] <= self.feature_threshold) self.left.fit(X[idxs_l, :], y[idxs_l]) self.right.fit(X[idxs_r, :], y[idxs_r]) def __predict(self, x): if self.feature_idx == -1: return self.value if x[self.feature_idx] > self.feature_threshold: return self.left.__predict(x) else: return self.right.__predict(x) def predict(self, X): y = np.zeros(X.shape[0]) for i in range(X.shape[0]): y[i] = self.__predict(X[i]) return y 

Mari kita ukur waktu yang sekarang dihabiskan untuk pelatihan, dan bandingkan dengan analog dari Sklearn.

 %%time A = RegressionTreeFastMse(4, min_size=5) A.fit(X,y) test_mytree = A.predict(X) test_mytree 

 %%time model = DecisionTreeRegressor(max_depth=4) model.fit(X,y) test_sklearn = model.predict(X) 

• Untuk algoritme kami, kami dapatkan - waktu CPU: pengguna 3,11 s, sys: 2,7 ms, total: 3,11 s
  Waktu dinding: 3,11 dtk.
• Untuk algoritma dari Sklearn - waktu CPU: pengguna 45,9 ms, sys: 1,09 ms, total: 47 ms
  Waktu dinding: 45,7 ms.

Hasilnya sudah lebih menyenangkan. Baiklah, mari kita lebih lanjut meningkatkan algoritma.

3. RegressionTree () kelas dengan kombinasi fitur linear

Sekarang, dalam algoritma kami, hubungan antara atribut tidak digunakan dengan cara apa pun. Kami memperbaiki satu fitur dan hanya melihat partisi ruang orthogonal. Bagaimana cara belajar menggunakan hubungan linear antar atribut? Artinya, untuk mencari partisi terbaik tidak suka $$$a_ {feat} <x$ , dan $$$\ sum_ {i = 1} ^ K b_i * a_i <x$ dimana $$$K$ - Apakah angka lebih kecil dari dimensi ruang kita?

Ada banyak pilihan, saya akan menyoroti dua yang paling menarik dari sudut pandang saya. Kedua pendekatan ini dijelaskan dalam buku Friedman (ia menemukan pohon-pohon ini).

Saya akan memberikan gambar sehingga jelas apa yang dimaksud:



Pertama, Anda dapat mencoba menemukan partisi linear ini secara algoritmik. Jelaslah bahwa mustahil untuk memilah-milah semua kombinasi linier, karena ada jumlah tak terhingga dari kombinasi, sehingga algoritma semacam itu harus serakah, yaitu, pada setiap iterasi, meningkatkan hasil iterasi sebelumnya. Gagasan utama dari algoritma ini dapat dibaca dalam buku ini, saya juga akan meninggalkan tautan di sini ke repositori teman dan kolega saya dengan penerapan algoritma ini.

Kedua, jika kita tidak jauh dari ide menemukan partisi ortogonal terbaik, lalu bagaimana kita memodifikasi dataset sehingga informasi tentang hubungan fitur digunakan dan pencarian didasarkan pada partisi ortogonal? Itu benar, untuk membuat semacam transformasi fitur asli menjadi yang baru. Misalnya, Anda dapat mengambil jumlah dari beberapa kombinasi fitur dan mencari partisi dengan mereka. Metode seperti itu lebih cocok dengan konsep algoritmik, tetapi melakukan tugasnya - ia mencari partisi ortogonal yang sudah ada dalam semacam interkoneksi atribut.

Baiklah, mari kita implementasikan - kita akan menambahkan sebagai fitur baru, misalnya, semua jenis kombinasi jumlah fitur $$$i, j$ dimana $$$I <j$ . Saya perhatikan bahwa kompleksitas algoritma dalam hal ini akan meningkat, sudah jelas berapa kali. Nah, agar bisa dianggap lebih cepat, kita akan menggunakan cython.

 %load_ext Cython %%cython -a import itertools import numpy as np cimport numpy as np from itertools import * cdef class RegressionTreeCython: cdef public int max_depth cdef public int feature_idx cdef public int min_size cdef public int averages cdef public np.float64_t feature_threshold cdef public np.float64_t value cpdef RegressionTreeCython left cpdef RegressionTreeCython right def __init__(self, max_depth=3, min_size=4, averages=1): self.max_depth = max_depth self.min_size = min_size self.value = 0 self.averages = averages self.feature_idx = -1 self.feature_threshold = 0 self.left = None self.right = None def data_transform(self, np.ndarray[np.float64_t, ndim=2] X, list index_tuples): #   -       for i in index_tuples: #  ,       X = np.hstack((X, X[:, i[0]:(i[1]+1)].sum(axis=1).reshape(X.shape[0],1))) return X def fit(self, np.ndarray[np.float64_t, ndim=2] X, np.ndarray[np.float64_t, ndim=1] y): cpdef np.float64_t mean1 = 0.0 cpdef np.float64_t mean2 = 0.0 cpdef long N = X.shape[0] cpdef long N1 = X.shape[0] cpdef long N2 = 0 cpdef np.float64_t delta1 = 0.0 cpdef np.float64_t delta2 = 0.0 cpdef np.float64_t sm1 = 0.0 cpdef np.float64_t sm2 = 0.0 cpdef list index_tuples cpdef list stuff cpdef long idx = 0 cpdef np.float64_t prev_error1 = 0.0 cpdef np.float64_t prev_error2 = 0.0 cpdef long thres = 0 cpdef np.float64_t error = 0.0 cpdef np.ndarray[long, ndim=1] idxs cpdef np.float64_t x = 0.0 #        #  ,     if self.averages: stuff = list(range(0,X.shape[1],1)) index_tuples = list(combinations(stuff,2)) #    X = self.data_transform(X, index_tuples) #   -   y self.value = y.mean() #   - mse     (  , #     )   base_error = ((y - self.value) ** 2).sum() error = base_error flag = 0 #     if self.max_depth <= 1: return dim_shape = X.shape[1] left_value, right_value = 0, 0 for feat in range(dim_shape): prev_error1, prev_error2 = base_error, 0 idxs = np.argsort(X[:, feat]) #      mean1, mean2 = y.mean(), 0 sm1, sm2 = y.sum(), 0 N = X.shape[0] N1, N2 = N, 0 thres = 1 while thres < N - 1: N1 -= 1 N2 += 1 idx = idxs[thres] x = X[idx, feat] #   -        delta1 = (sm1 - y[idx]) * 1.0 / N1 - mean1 delta2 = (sm2 + y[idx]) * 1.0 / N2 - mean2 #   sm1 -= y[idx] sm2 += y[idx] #    O(1) prev_error1 += (delta1**2) * N1 prev_error1 -= (y[idx] - mean1)**2 prev_error1 -= 2 * delta1 * (sm1 - mean1 * N1) mean1 = sm1/N1 prev_error2 += (delta2**2) * N2 prev_error2 += (y[idx] - mean2)**2 prev_error2 -= 2 * delta2 * (sm2 - mean2 * N2) mean2 = sm2/N2 #       if thres < N - 1 and np.abs(x - X[idxs[thres + 1], feat]) < 1e-5: thres += 1 continue # 2    -   #   -      if (prev_error1 + prev_error2 < error): if (min(N1,N2) > self.min_size): #         self.feature_idx, self.feature_threshold = feat, x #     left_value, right_value = mean1, mean2 #  -     flag = 1 error = prev_error1 + prev_error2 thres += 1 # self.feature_idx -     . #   -  ,    -   #  ,   ,     #   ,  if self.feature_idx == -1: return #    self.left = RegressionTreeCython(self.max_depth - 1, averages=0) self.left.value = left_value self.right = RegressionTreeCython(self.max_depth - 1, averages=0) self.right.value = right_value #      idxs_l = (X[:, self.feature_idx] > self.feature_threshold) idxs_r = (X[:, self.feature_idx] <= self.feature_threshold) #   self.left.fit(X[idxs_l, :], y[idxs_l]) self.right.fit(X[idxs_r, :], y[idxs_r]) def __predict(self, np.ndarray[np.float64_t, ndim=1] x): if self.feature_idx == -1: return self.value if x[self.feature_idx] > self.feature_threshold: return self.left.__predict(x) else: return self.right.__predict(x) def predict(self, np.ndarray[np.float64_t, ndim=2] X): #   ,        if self.averages: stuff = list(range(0,X.shape[1],1)) index_tuples = list(itertools.combinations(stuff,2)) X = self.data_transform(X, index_tuples) y = np.zeros(X.shape[0]) for i in range(X.shape[0]): y[i] = self.__predict(X[i]) return y 

4. Perbandingan hasil

Baiklah, mari kita bandingkan hasilnya. Kami akan membandingkan tiga algoritma dengan parameter yang sama - pohon dari Sklearn, pohon biasa dan pohon kami dengan fitur baru. Kami akan membagi set data kami menjadi beberapa set pelatihan dan tes, dan menghitung kesalahan.

 from sklearn.model_selection import KFold def get_metrics(X,y,n_folds=2, model=None): kf = KFold(n_splits=n_folds, shuffle=True) kf.get_n_splits(X) er_list = [] for train_index, test_index in kf.split(X): X_train, X_test = X[train_index], X[test_index] y_train, y_test = y[train_index], y[test_index] model.fit(X_train,y_train) predict = model.predict(X_test) er_list.append(mse(y_test, predict)) return er_list 

Sekarang mari kita jalankan semua algoritma.

 import matplotlib.pyplot as plt data = datasets.fetch_california_housing() X = np.array(data.data) y = np.array(data.target) er_sklearn_tree = get_metrics(X,y,30,DecisionTreeRegressor(max_depth=4, min_samples_leaf=10)) er_fast_mse_tree = get_metrics(X,y,30,RegressionTreeFastMse(4, min_size=10)) er_averages_tree = get_metrics(X,y,30,RegressionTreeCython(4, min_size=10)) %matplotlib inline data = [er_sklearn_tree, er_fast_mse_tree, er_averages_tree] fig7, ax7 = plt.subplots() ax7.set_title('') ax7.boxplot(data, labels=['Sklearn Tree', 'Fast Mse Tree', 'Averages Tree']) plt.grid() plt.show() 

Hasil:



Pohon reguler kami hilang dari Sklearn (yang bisa dimengerti: Sklearn dioptimalkan dengan baik, dan secara default masih ada banyak parameter di pohon yang tidak kami perhitungkan), tetapi ketika menambahkan jumlah, hasilnya menjadi lebih menyenangkan.

Untuk meringkas: kami belajar bagaimana menulis pohon yang menentukan dari awal, belajar bagaimana meningkatkan kinerja mereka dan menguji efektivitasnya pada dataset nyata dengan membandingkannya dengan algoritma dari Sklearn. Namun, metode yang disajikan di sini tidak membatasi peningkatan algoritma, jadi perlu diingat bahwa kode yang diusulkan dapat dibuat lebih baik. Pada artikel selanjutnya, kami akan menulis peningkatan berdasarkan algoritma ini.

Semua sukses!