Menulis XGBoost dari awal - bagian 2: meningkatkan gradien

Halo semuanya!

Dalam artikel terakhir, kami menemukan bagaimana pohon keputusan diatur, dan dari awal kami menerapkannya
algoritma konstruksi, sekaligus mengoptimalkan dan memperbaikinya. Pada artikel ini, kita akan menerapkan algoritma peningkatan gradien dan pada akhirnya kita akan membuat XGBoost kita sendiri. Narasi akan mengikuti pola yang sama: kita menulis sebuah algoritma, mendeskripsikannya, meringkasnya dengan membandingkan hasil kerja dengan analog dari Sklearn.

Dalam artikel ini, penekanan juga akan ditempatkan pada implementasi dalam kode, oleh karena itu lebih baik untuk membaca seluruh teori bersama di yang lain (misalnya, dalam kursus ODS ), dan sudah dengan pengetahuan teori, Anda dapat melanjutkan ke artikel ini, karena topiknya agak rumit.



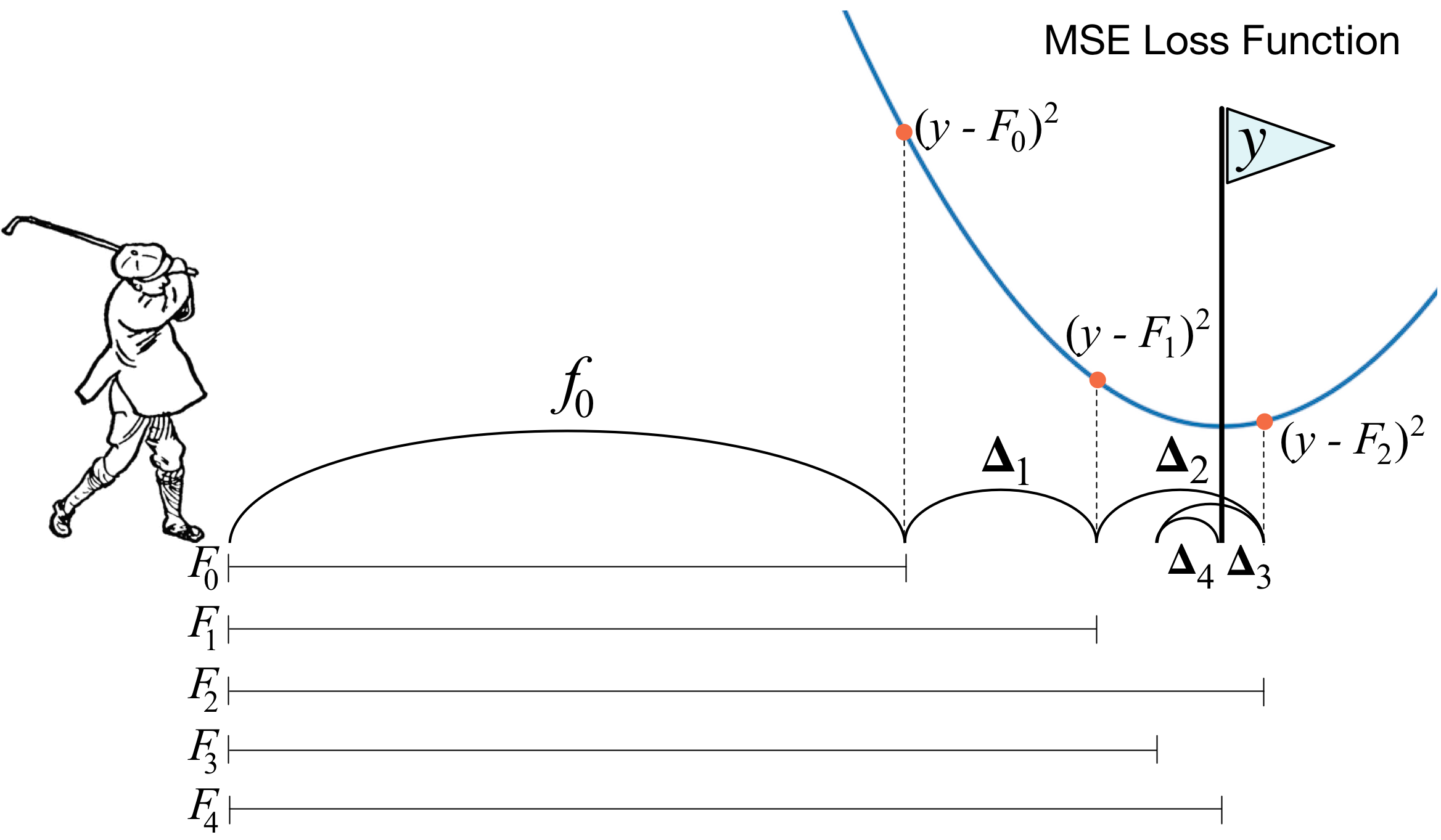
Apa yang dimaksud dengan peningkatan gradien? Gambar pegolf dengan sempurna menggambarkan ide utama. Untuk mendorong bola ke dalam lubang, pegolf membuat setiap pukulan berikutnya dengan mempertimbangkan pengalaman pukulan sebelumnya - baginya ini adalah kondisi yang diperlukan untuk memasukkan bola ke dalam lubang. Jika itu sangat kasar (saya bukan ahli golf :)), maka dengan setiap pukulan baru hal pertama yang dilihat pegolf adalah jarak antara bola dan lubang setelah pukulan sebelumnya. Dan tugas utama adalah mengurangi jarak ini dengan pukulan berikutnya.

Meningkatkan dibangun dengan cara yang sangat mirip. Pertama, kita perlu memperkenalkan definisi "lubang", yaitu tujuan yang akan kita perjuangkan. Kedua, kita harus belajar memahami sisi mana yang harus kita kalahkan dengan klub agar bisa lebih dekat dengan target. Ketiga, dengan mempertimbangkan semua aturan ini, Anda harus membuat urutan pukulan yang benar sehingga setiap aturan berikutnya mengurangi jarak antara bola dan lubang.

Sekarang kami memberikan definisi yang sedikit lebih ketat. Kami memperkenalkan model pemungutan suara tertimbang:

$$

$$h (x) = \ sum_ {i = 1} ^ nb_ia_i, x \ in X, b_i \ in R$$

Di sini $$$X$ Apakah ruang dari mana kita mengambil benda, $$$b_i, a_i$ - ini adalah koefisien di depan model dan model itu sendiri, yaitu pohon keputusan. Misalkan sudah beberapa langkah, menggunakan aturan yang dijelaskan, itu mungkin untuk menambah komposisi $$$T-1$ algoritma lemah. Untuk belajar memahami apa jenis algoritma yang harus di langkah $$$T$ , kami memperkenalkan fungsi kesalahan:

$$$err (h) = \ sum_ {j = 1} ^ N L (\ sum_ {i = 1} ^ {T-1} a_ib_i (x_j) + b_Ta_T (x_j)) \ rightarrow min_ {a_T, b_T}$

Ternyata algoritma terbaik akan menjadi yang dapat meminimalkan kesalahan yang diterima pada iterasi sebelumnya. Dan karena dorongannya adalah gradien, maka fungsi kesalahan ini harus memiliki vektor anti-gradien yang dapat Anda gunakan untuk mencari minimum. Itu saja!

Segera sebelum implementasi, saya akan menambahkan beberapa kata tentang bagaimana semuanya akan diatur bersama kami. Seperti pada artikel sebelumnya, kami menganggap MSE sebagai kerugian. Mari kita hitung gradiennya:

$$

$$mse (y, prediksikan) = (y - prediksi) ^ 2 \\ \ nabla_ {prediksi} mse (y, prediksi) = prediksi - y$$

Dengan demikian, vektor antigradien akan sama dengan $$$y - prediksi$ . Di langkah $$$i$ kami mempertimbangkan kesalahan algoritma yang diperoleh pada iterasi sebelumnya. Selanjutnya, kami melatih algoritma baru kami pada kesalahan ini, dan kemudian menambahkannya ke ensemble kami dengan tanda minus dan beberapa koefisien.

Sekarang mari kita mulai.

1. Implementasi kelas meningkatkan gradien biasa

import pandas as pd import matplotlib.pyplot as plt import numpy as np from tqdm import tqdm_notebook from sklearn import datasets from sklearn.metrics import mean_squared_error as mse from sklearn.tree import DecisionTreeRegressor import itertools %matplotlib inline %load_ext Cython %%cython -a import itertools import numpy as np cimport numpy as np from itertools import * cdef class RegressionTreeFastMse: cdef public int max_depth cdef public int feature_idx cdef public int min_size cdef public int averages cdef public np.float64_t feature_threshold cdef public np.float64_t value cpdef RegressionTreeFastMse left cpdef RegressionTreeFastMse right def __init__(self, max_depth=3, min_size=4, averages=1): self.max_depth = max_depth self.min_size = min_size self.value = 0 self.feature_idx = -1 self.feature_threshold = 0 self.left = None self.right = None def fit(self, np.ndarray[np.float64_t, ndim=2] X, np.ndarray[np.float64_t, ndim=1] y): cpdef np.float64_t mean1 = 0.0 cpdef np.float64_t mean2 = 0.0 cpdef long N = X.shape[0] cpdef long N1 = X.shape[0] cpdef long N2 = 0 cpdef np.float64_t delta1 = 0.0 cpdef np.float64_t delta2 = 0.0 cpdef np.float64_t sm1 = 0.0 cpdef np.float64_t sm2 = 0.0 cpdef list index_tuples cpdef list stuff cpdef long idx = 0 cpdef np.float64_t prev_error1 = 0.0 cpdef np.float64_t prev_error2 = 0.0 cpdef long thres = 0 cpdef np.float64_t error = 0.0 cpdef np.ndarray[long, ndim=1] idxs cpdef np.float64_t x = 0.0 #   -   y self.value = y.mean() #   - mse     base_error = ((y - self.value) ** 2).sum() error = base_error flag = 0 #     if self.max_depth <= 1: return dim_shape = X.shape[1] left_value, right_value = 0, 0 for feat in range(dim_shape): prev_error1, prev_error2 = base_error, 0 idxs = np.argsort(X[:, feat]) #      mean1, mean2 = y.mean(), 0 sm1, sm2 = y.sum(), 0 N = X.shape[0] N1, N2 = N, 0 thres = 1 while thres < N - 1: N1 -= 1 N2 += 1 idx = idxs[thres] x = X[idx, feat] #   -  ,  ,    delta1 = (sm1 - y[idx]) * 1.0 / N1 - mean1 delta2 = (sm2 + y[idx]) * 1.0 / N2 - mean2 #   sm1 -= y[idx] sm2 += y[idx] #    O(1) prev_error1 += (delta1**2) * N1 prev_error1 -= (y[idx] - mean1)**2 prev_error1 -= 2 * delta1 * (sm1 - mean1 * N1) mean1 = sm1/N1 prev_error2 += (delta2**2) * N2 prev_error2 += (y[idx] - mean2)**2 prev_error2 -= 2 * delta2 * (sm2 - mean2 * N2) mean2 = sm2/N2 #       if thres < N - 1 and np.abs(x - X[idxs[thres + 1], feat]) < 1e-5: thres += 1 continue if (prev_error1 + prev_error2 < error): if (min(N1,N2) > self.min_size): #         self.feature_idx, self.feature_threshold = feat, x #     left_value, right_value = mean1, mean2 #  -     flag = 1 error = prev_error1 + prev_error2 thres += 1 #   ,  if self.feature_idx == -1: return #    self.left = RegressionTreeFastMse(self.max_depth - 1) self.left.value = left_value self.right = RegressionTreeFastMse(self.max_depth - 1) self.right.value = right_value #      idxs_l = (X[:, self.feature_idx] > self.feature_threshold) idxs_r = (X[:, self.feature_idx] <= self.feature_threshold) #   self.left.fit(X[idxs_l, :], y[idxs_l]) self.right.fit(X[idxs_r, :], y[idxs_r]) def __predict(self, np.ndarray[np.float64_t, ndim=1] x): if self.feature_idx == -1: return self.value if x[self.feature_idx] > self.feature_threshold: return self.left.__predict(x) else: return self.right.__predict(x) def predict(self, np.ndarray[np.float64_t, ndim=2] X): y = np.zeros(X.shape[0]) for i in range(X.shape[0]): y[i] = self.__predict(X[i]) return y 

 class GradientBoosting(): def __init__(self, n_estimators=100, learning_rate=0.1, max_depth=3, random_state=17, n_samples = 15, min_size = 5, base_tree='Bagging'): self.n_estimators = n_estimators self.max_depth = max_depth self.learning_rate = learning_rate self.initialization = lambda y: np.mean(y) * np.ones([y.shape[0]]) self.min_size = min_size self.loss_by_iter = [] self.trees_ = [] self.loss_by_iter_test = [] self.n_samples = n_samples self.base_tree = base_tree def fit(self, X, y): self.X = X self.y = y b = self.initialization(y) prediction = b.copy() for t in tqdm_notebook(range(self.n_estimators)): if t == 0: resid = y else: #    resid = (y - prediction) #    if self.base_tree == 'Bagging': tree = Bagging(max_depth=self.max_depth, min_size = self.min_size) if self.base_tree == 'Tree': tree = RegressionTreeFastMse(max_depth=self.max_depth, min_size = self.min_size) #     tree.fit(X, resid) #        b = tree.predict(X).reshape([X.shape[0]]) self.trees_.append(tree) prediction += self.learning_rate * b #       if t > 0: self.loss_by_iter.append(mse(y,prediction)) return self def predict(self, X): #   –          pred = np.ones([X.shape[0]]) * np.mean(self.y) #    for t in range(self.n_estimators): pred += self.learning_rate * self.trees_[t].predict(X).reshape([X.shape[0]]) return pred 

Kami sekarang akan menyusun kurva kehilangan pada set pelatihan untuk memastikan bahwa pada setiap iterasi kami benar-benar mengalami penurunan.

 GDB = GradientBoosting(n_estimators=50) GDB.fit(X,y) x = GDB.predict(X) plt.grid() plt.title('Loss by iterations') plt.plot(GDB.loss_by_iter) 

2. Mengantongi pohon yang menentukan

Nah, sebelum kita membandingkan hasilnya, mari kita bicara tentang prosedur mengantongi pohon.

Semuanya sederhana di sini: kami ingin melindungi diri dari pelatihan ulang, dan oleh karena itu, dengan bantuan pengambilan sampel dengan pengembalian, kami akan meratakan prediksi kami agar tidak secara tidak sengaja bertemu dengan pencilan (mengapa bekerja seperti ini, baca tautan dengan lebih baik).

 class Bagging(): '''  Bagging -      . ''' def __init__(self, max_depth = 3, min_size=10, n_samples = 10): #super(CART, self).__init__() self.max_depth = max_depth self.min_size = min_size self.n_samples = n_samples self.subsample_size = None self.list_of_Carts = [RegressionTreeFastMse(max_depth=self.max_depth, min_size=self.min_size) for _ in range(self.n_samples)] def get_bootstrap_samples(self, data_train, y_train): #      indices = np.random.randint(0, len(data_train), (self.n_samples, self.subsample_size)) samples_train = data_train[indices] samples_y = y_train[indices] return samples_train, samples_y def fit(self, data_train, y_train): #    self.subsample_size = int(data_train.shape[0]) samples_train, samples_y = self.get_bootstrap_samples(data_train, y_train) for i in range(self.n_samples): self.list_of_Carts[i].fit(samples_train[i], samples_y[i].reshape(-1)) return self def predict(self, test_data): #        num_samples = test_data.shape[0] pred = [] for i in range(self.n_samples): pred.append(self.list_of_Carts[i].predict(test_data)) pred = np.array(pred).T return np.array([np.mean(pred[i]) for i in range(num_samples)]) 

Nah, sekarang sebagai algoritma dasar kita dapat menggunakan bukan hanya satu pohon, tetapi mengantongi dari pohon - jadi sekali lagi, kita akan melindungi diri kita dari pelatihan ulang.

3. Hasil

Bandingkan hasil dari algoritma kami.

 from sklearn.model_selection import KFold import matplotlib.pyplot as plt from sklearn.ensemble import GradientBoostingRegressor as GDBSklearn import copy def get_metrics(X,y,n_folds=2, model=None): kf = KFold(n_splits=n_folds, shuffle=True) kf.get_n_splits(X) er_list = [] for train_index, test_index in tqdm_notebook(kf.split(X)): X_train, X_test = X[train_index], X[test_index] y_train, y_test = y[train_index], y[test_index] model.fit(X_train,y_train) predict = model.predict(X_test) er_list.append(mse(y_test, predict)) return er_list data = datasets.fetch_california_housing() X = np.array(data.data) y = np.array(data.target) er_boosting = get_metrics(X,y,30,GradientBoosting(max_depth=3, n_estimators=40, base_tree='Tree' )) er_boobagg = get_metrics(X,y,30,GradientBoosting(max_depth=3, n_estimators=40, base_tree='Bagging' )) er_sklearn_boosting = get_metrics(X,y,30,GDBSklearn(max_depth=3,n_estimators=40, learning_rate=0.1)) %matplotlib inline data = [er_sklearn_boosting, er_boosting, er_boobagg] fig7, ax7 = plt.subplots() ax7.set_title('') ax7.boxplot(data, labels=['Sklearn Boosting', 'Boosting', 'BooBag']) plt.grid() plt.show() 

Diterima:



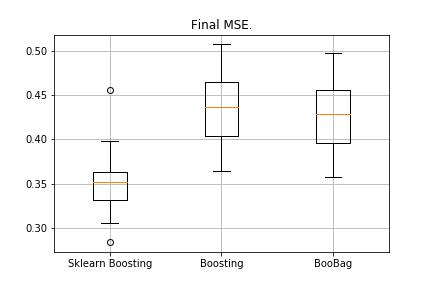
Kami belum dapat mengalahkan analog dari Sklearn, karena sekali lagi kami tidak memperhitungkan banyak parameter yang digunakan dalam metode ini . Namun, kami melihat bahwa mengantongi sedikit membantu.

Jangan putus asa, dan lanjutkan menulis XGBoost.

4. XGBoost

Sebelum membaca lebih lanjut, saya sangat menyarankan Anda untuk membiasakan diri dengan video berikutnya, yang menjelaskan teorinya dengan sangat baik.

Ingat kesalahan apa yang kami perkecil dalam peningkatan normal:

$$

$$err (h) = \ sum_ {j = 1} ^ N L (\ sum_ {i = 1} ^ {T-1} a_ib_i (x_j) + b_Ta_T (x_j))$$

XGBoost secara eksplisit menambahkan regularisasi ke fungsi kesalahan ini:

$$

$$err (h) = \ sum_ {j = 1} ^ NL (\ sum_ {i = 1} ^ {T-1} a_ib_i (x_j) + b_Ta_T (x_j)) + \ sum_ {i = 1} ^ T \ omega (a_i)$$

Bagaimana cara mempertimbangkan fungsi ini? Pertama, kami memperkirakannya dengan bantuan seri Taylor orde kedua, di mana algoritma baru dianggap sebagai kenaikan di mana kami akan bergerak, dan kemudian kami sudah melukis tergantung pada jenis kerugian yang kami miliki:

$$$f (x + \ delta x) \ thickapprox f (x) + f (x) '\ delta x + 0,5 * f (x)' '(\ delta x) ^ 2$

Kita perlu menentukan pohon mana yang akan kita anggap buruk dan mana yang baik.

Ingat kembali dengan prinsip apa regresi dibangun $$$L_2$ -regularisasi - semakin normal nilai-nilai koefisien sebelum regresi, semakin buruk, oleh karena itu, mereka perlu sekecil mungkin.

Dalam XGBoost, idenya sangat mirip: pohon itu didenda jika jumlah norma nilai dalam daun di dalamnya sangat besar. Oleh karena itu, kompleksitas pohon diperkenalkan sebagai berikut:

$$

$$\ omega (a) = \ gamma Z + 0,5 * \ sum_ {i = 1} ^ {Z} w_i ^ 2$$

$$$w$ - nilai dalam daun, $$$Z$ - jumlah daun.

Ada formula transisi dalam video, kami tidak akan menampilkannya di sini. Itu semua bermuara pada kenyataan bahwa kita akan memilih partisi baru, memaksimalkan keuntungan:

$$

$$Penguatan = \ frac {G_l ^ 2} {S_l ^ 2 + \ lambda} + \ frac {G_r ^ 2} {S_r ^ 2 + \ lambda} - \ frac {(G_l + G_r) ^ 2} {S_l ^ 2 + S_r ^ 2 + \ lambda} - \ gamma$$

Di sini $$$\ gamma, \ lambda$ Apakah parameter numerik regularisasi, dan $$$G_i, S_i$ - jumlah yang sesuai dari turunan pertama dan kedua untuk partisi ini.

Itu saja, teorinya sangat singkat, tautan diberikan, sekarang mari kita bicara tentang apa turunannya jika kita bekerja dengan MSE. Sederhana:

$$$mse (y, prediksi) = (y - prediksi) ^ 2 \\ \ nabla_ {predict} mse (y, predict) = prediksi - y \\ \ nabla_ {predict} ^ 2 mse (y, prediksi) = 1$

Kapan kami akan menghitung jumlahnya $$$G_i, S_i$ , cukup tambahkan yang pertama $$$prediksi - y$ dan yang kedua hanyalah kuantitas.

 %%cython -a import numpy as np cimport numpy as np cdef class RegressionTreeGain: cdef public int max_depth cdef public np.float64_t gain cdef public np.float64_t lmd cdef public np.float64_t gmm cdef public int feature_idx cdef public int min_size cdef public np.float64_t feature_threshold cdef public np.float64_t value cpdef public RegressionTreeGain left cpdef public RegressionTreeGain right def __init__(self, int max_depth=3, np.float64_t lmd=1.0, np.float64_t gmm=0.1, min_size=5): self.max_depth = max_depth self.gmm = gmm self.lmd = lmd self.left = None self.right = None self.feature_idx = -1 self.feature_threshold = 0 self.value = -1e9 self.min_size = min_size return def fit(self, np.ndarray[np.float64_t, ndim=2] X, np.ndarray[np.float64_t, ndim=1] y): cpdef long N = X.shape[0] cpdef long N1 = X.shape[0] cpdef long N2 = 0 cpdef long idx = 0 cpdef long thres = 0 cpdef np.float64_t gl, gr, gn cpdef np.ndarray[long, ndim=1] idxs cpdef np.float64_t x = 0.0 cpdef np.float64_t best_gain = -self.gmm if self.value == -1e9: self.value = y.mean() base_error = ((y - self.value) ** 2).sum() error = base_error flag = 0 if self.max_depth <= 1: return dim_shape = X.shape[1] left_value = 0 right_value = 0 #    # -  -   mse, L = (y - pred)**2 # dL/dpred = pred - y,          - # dL^2/d^2pred = 1 - ,       for feat in range(dim_shape): idxs = np.argsort(X[:, feat]) gl,gr = y.sum(),0.0 N1, N2, thres = N, 0, 0 while thres < N - 1: N1 -= 1 N2 += 1 idx = idxs[thres] x = X[idx, feat] gl -= y[idx] gr += y[idx] #   gn = (gl**2) / (N1 + self.lmd) + (gr**2) / (N2 + self.lmd) gn -= ((gl + gr)**2) / (N1 + N2 + self.lmd) + self.gmm if thres < N - 1 and x == X[idxs[thres + 1], feat]: thres += 1 continue #     if (gn > best_gain) and (min(N1,N2) > self.min_size): flag = 1 best_gain = gn left_value = -gl / (N1 + self.lmd) right_value = -gr / (N2 + self.lmd) self.feature_idx = feat self.feature_threshold = x thres += 1 self.gain = best_gain if self.feature_idx == -1: return self.left = RegressionTreeGain(max_depth=self.max_depth - 1, gmm=self.gmm, lmd=self.lmd) self.left.value = left_value self.right = RegressionTreeGain(max_depth=self.max_depth - 1, gmm=self.gmm, lmd=self.lmd) self.right.value = right_value idxs_l = (X[:, self.feature_idx] > self.feature_threshold) idxs_r = (X[:, self.feature_idx] <= self.feature_threshold) self.left.fit(X[idxs_l, :], y[idxs_l]) self.right.fit(X[idxs_r, :], y[idxs_r]) #    if (self.left.left == None or self.right.left == None): if self.gain < 0.0: self.left = None self.right = None self.feature_idx = -1 def __predict(self, np.ndarray[np.float64_t, ndim=1] x): if self.feature_idx == -1: return self.value if x[self.feature_idx] > self.feature_threshold: return self.left.__predict(x) else: return self.right.__predict(x) def predict(self, np.ndarray[np.float64_t, ndim=2] X): y = np.zeros(X.shape[0]) for i in range(X.shape[0]): y[i] = self.__predict(X[i]) return y 

Klarifikasi kecil: untuk membuat formula di pohon dengan mendapatkan lebih indah, sebagai gantinya kita melatih target dengan tanda minus.

Kami sedikit memodifikasi boosting kami, membuat beberapa parameter adaptif. Misalnya, jika kami melihat bahwa kerugian telah mulai mencapai dataran tinggi, maka kami mengurangi tingkat pembelajaran dan meningkatkan max_depth untuk estimator berikut. Kami juga akan menambahkan bagging baru - sekarang kami akan mendorong baggings pohon dengan keuntungan:

 class Bagging(): def __init__(self, max_depth = 3, min_size=5, n_samples = 10): self.max_depth = max_depth self.min_size = min_size self.n_samples = n_samples self.subsample_size = None self.list_of_Carts = [RegressionTreeGain(max_depth=self.max_depth, min_size=self.min_size) for _ in range(self.n_samples)] def get_bootstrap_samples(self, data_train, y_train): indices = np.random.randint(0, len(data_train), (self.n_samples, self.subsample_size)) samples_train = data_train[indices] samples_y = y_train[indices] return samples_train, samples_y def fit(self, data_train, y_train): self.subsample_size = int(data_train.shape[0]) samples_train, samples_y = self.get_bootstrap_samples(data_train, y_train) for i in range(self.n_samples): self.list_of_Carts[i].fit(samples_train[i], samples_y[i].reshape(-1)) return self def predict(self, test_data): num_samples = test_data.shape[0] pred = [] for i in range(self.n_samples): pred.append(self.list_of_Carts[i].predict(test_data)) pred = np.array(pred).T return np.array([np.mean(pred[i]) for i in range(num_samples)]) 

 class GradientBoosting(): def __init__(self, n_estimators=100, learning_rate=0.2, max_depth=3, random_state=17, n_samples = 15, min_size = 5, base_tree='Bagging'): self.n_estimators = n_estimators self.max_depth = max_depth self.learning_rate = learning_rate self.initialization = lambda y: np.mean(y) * np.ones([y.shape[0]]) self.min_size = min_size self.loss_by_iter = [] self.trees_ = [] self.loss_by_iter_test = [] self.n_samples = n_samples self.base_tree = base_tree #  -       #   ,   lr   max_depth self.add_to_max_depth = 1 self.init_mse_board = 1.5 def fit(self, X, y): print (self.base_tree) self.X = X self.y = y b = self.initialization(y) prediction = b.copy() for t in tqdm_notebook(range(self.n_estimators)): if t == 0: resid = y else: resid = (y - prediction) if (mse(temp_resid,resid) < self.init_mse_board): self.init_mse_board /= 1.5 self.add_to_max_depth += 1 self.learning_rate /= 1.1 # print ('Alert!', t, self.add_to_max_depth) if self.base_tree == 'Bagging': tree = Bagging(max_depth=self.max_depth+self.add_to_max_depth, min_size = self.min_size) resid = -resid if self.base_tree == 'Tree': tree = RegressionTreeFastMse(max_depth=self.max_depth+self.add_to_max_depth, min_size = self.min_size) if self.base_tree == 'XGBoost': tree = RegressionTreeGain(max_depth=self.max_depth+self.add_to_max_depth, min_size = self.min_size) resid = -resid tree.fit(X, resid) b = tree.predict(X).reshape([X.shape[0]]) # print (b.shape) self.trees_.append(tree) prediction += self.learning_rate * b temp_resid = resid return self def predict(self, X): #   –          pred = np.ones([X.shape[0]]) * np.mean(self.y) #    for t in range(self.n_estimators): pred += self.learning_rate * self.trees_[t].predict(X).reshape([X.shape[0]]) return pred 

5. Hasil

Secara tradisi, kami membandingkan hasilnya:

 data = datasets.fetch_california_housing() X = np.array(data.data) y = np.array(data.target) import matplotlib.pyplot as plt from sklearn.ensemble import GradientBoostingRegressor as GDBSklearn er_boosting_bagging = get_metrics(X,y,30,GradientBoosting(max_depth=3, n_estimators=150,base_tree='Bagging')) er_boosting_xgb = get_metrics(X,y,30,GradientBoosting(max_depth=3, n_estimators=150,base_tree='XGBoost')) er_sklearn_boosting = get_metrics(X,y,30,GDBSklearn(max_depth=3,n_estimators=150,learning_rate=0.2)) %matplotlib inline data = [er_sklearn_boosting, er_boosting_xgb, er_boosting_bagging] fig7, ax7 = plt.subplots() ax7.set_title('') ax7.boxplot(data, labels=['GdbSklearn', 'Xgboost', 'XGBooBag']) plt.grid() plt.show() 

Gambarannya adalah sebagai berikut:



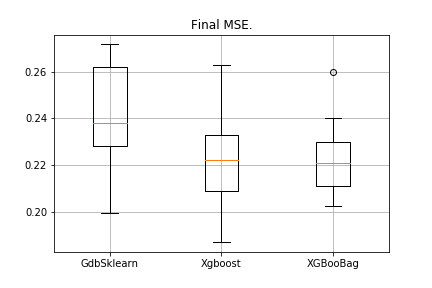
XGBoost memiliki kesalahan terendah, tetapi XGBooBag memiliki kesalahan lebih ramai, yang jelas lebih baik: algoritma lebih stabil.

Itu saja. Saya sangat berharap bahwa materi yang disajikan dalam dua artikel bermanfaat, dan Anda dapat mempelajari sesuatu yang baru untuk diri Anda sendiri. Saya mengucapkan terima kasih khusus kepada Dmitry untuk umpan balik yang komprehensif dan kode sumber, kepada Anton untuk saran, dan Vladimir untuk tugas yang sulit untuk belajar.

Semua sukses!