Cara Kerja PageRank: Menerapkan dalam R melalui Aljabar Linier dan Metode Daya

Halo, warga Habrovsk!

Nama saya Alex. Kali ini saya menyiarkan dari tempat kerja di ITAR-TASS.

Dalam teks singkat ini, saya akan memperkenalkan metode penghitungan PageRank kepada Anda (selanjutnya saya akan menyebutnya PR) menggunakan contoh-contoh sederhana dan mudah dipahami, dalam bahasa R. Algoritme adalah properti intelektual Google, tetapi, karena kegunaannya untuk tugas analisis data, banyak tugas digunakan , yang dapat direduksi menjadi mencari node besar dalam grafik dan memeringkatnya berdasarkan kepentingan.

Menyebutkan perusahaan besar dalam sebuah posting bukanlah iklan.

Karena saya bukan ahli matematika profesional, saya menggunakan - dan merekomendasikan kepada Anda - artikel ini dan tutorial ini sebagai panduan.

Pemahaman PR yang intuitif

Memahami cara kerjanya tidak sulit. Ada satu set elemen yang saling berhubungan. Inilah cara tepatnya mereka terhubung - ini adalah pertanyaan luas: mungkin melalui tautan (seperti Google), mungkin dengan menyebutkan satu sama lain (tautan yang hampir sama), probabilitas transisi antar elemen (matriks proses Markov) dapat menjadi apriori yang ditentukan tanpa menentukan fisik. arti komunikasi. Saya ingin menugaskan elemen-elemen ini kriteria penting tertentu, yang akan membawa informasi tentang kemungkinan bahwa elemen ini akan dikunjungi oleh beberapa partikel abstrak yang bergerak melalui grafik dalam proses difusi.

Um, itu tidak terdengar terlalu jelas. Lebih mudah membayangkan seorang pria menggunakan laptop dengan opium , menjelajahi halaman hasil pencarian, merokok hookah, mengikuti tautan dari satu halaman ke halaman lainnya dan semakin sering muncul di halaman (atau halaman) yang sama.

Ini disebabkan oleh kenyataan bahwa beberapa halaman yang dia kunjungi mengandung informasi menarik di sumber aslinya sehingga halaman lain dipaksa untuk mencetaknya kembali dengan indikasi tautan.

Orang seperti itu di Google bernama Surfer acak. Dia adalah partikel dalam proses difusi: perubahan posisi diskrit pada grafik dari waktu ke waktu. Dan kemungkinan dia mengunjungi halaman dengan waktu difusi yang cenderung tak terhingga adalah PR.

Implementasi sederhana perhitungan PR

Mari kita setuju - kita bekerja dengan 10 elemen, dalam grafik kecil yang kecil dan nyaman.

# clear environment rm(list = ls()); gc() ## load libs library(data.table) library(magrittr) library(markovchain) ## dummy data number_nodes <- 10 node_names <- letters[seq_len(number_nodes)] set.seed(1) nodes <- sapply( seq_len(number_nodes), function(x) { paste( c( node_names[-x] , sample(node_names[-x], sample(1:5, 1), replace = T) ) , collapse = ' ' ) } ) names(nodes) <- node_names print( paste(nodes, collapse = '; ') ) ## make long dt dt <- data.table( citing_node = node_names , cited_node = nodes ) %>% .[, .(cited_node = unlist(strsplit(cited_node, ' '))), by = citing_node] %>% dcast( . , cited_node ~ citing_node , fun.aggregate = length ) dt apply(dt[,-1,with=F], 2, sum) ## affinity matrix A <- as.matrix(dt[, 2:dim(dt)[2]]) A <- sweep(A, 2, colSums(A), `/`) A[is.nan(A)] <- 0 rowSums(A) colSums(A) mark <- new("markovchain", transitionMatrix = t(A), states = node_names, name = "mark") plot(mark) 

Masing-masing dari 10 elemen (node) berisi 10 hingga 14 referensi ke node lain dalam urutan acak, tidak termasuk dirinya sendiri. Untuk saat ini, kami hanya memutuskan bahwa data yang disebutkan adalah tautan web.

Jelas bahwa beberapa elemen disebutkan lebih sering daripada yang lain. Lihat ini.

Omong-omong, saya sarankan menggunakan paket data.table untuk eksperimen. Sehubungan dengan prinsip-prinsip Tidyverse, semuanya ternyata efisien dan cepat.

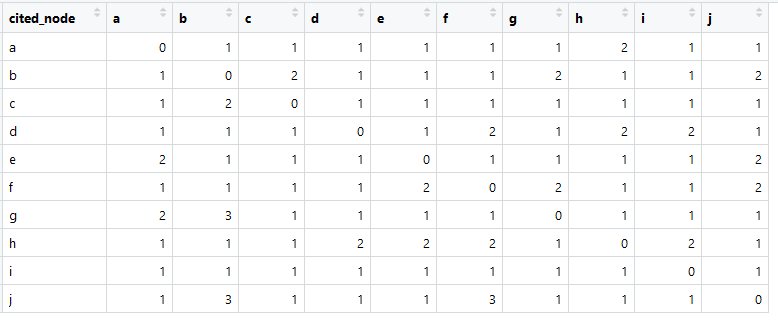
Beginilah tampilan matriks tautan kami (paling sering disebut matriks adjacency).

Jumlah dalam setiap kolom lebih besar dari nol, yang berarti bahwa ada hubungan dari setiap elemen dengan beberapa elemen lain (ini penting untuk analisis lebih lanjut).

> berlaku (dt [, - 1, dengan = F], 2, jumlah)
abcdefghij
11 14 10 10 11 13 11 11 11 12

Berdasarkan tabel ini, kita dapat membuat apa yang disebut matriks Afinitas, atau, menurut pendapat kami, matriks kedekatan (dan juga disebut matriks transisi), yang oleh para ahli matematika disebut matriks stokastik (matriks kolom-stokastik): sumber utama

Tetapkan ke variabel bernama A.



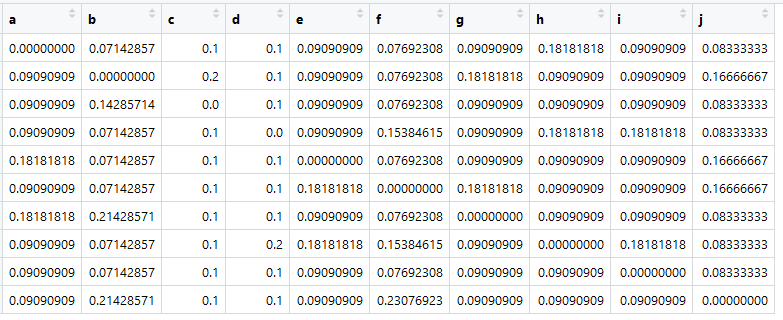
Yang paling penting sekarang adalah jumlah dalam semua kolom sama dengan satu.

> colSums (A)
abcdefghij
1 1 1 1 1 1 1 1 1 1

Ini dia - matriks transisi, itu Markov, itu persamaan. Angka adalah probabilitas transisi dari elemen dalam kolom ke elemen dalam satu baris.

Ini, tentu saja, bukan "kesamaan" yang nyata. Hadiah akan, misalnya, jika kita menghitung kosinus sudut antara penyajian dokumen. Tetapi penting bahwa matriks transisi direduksi menjadi probabilitas (pseudo-) sehingga jumlah dari setiap kolom sama dengan satu.

Mari kita lihat grafik transisi Markov (A kami):



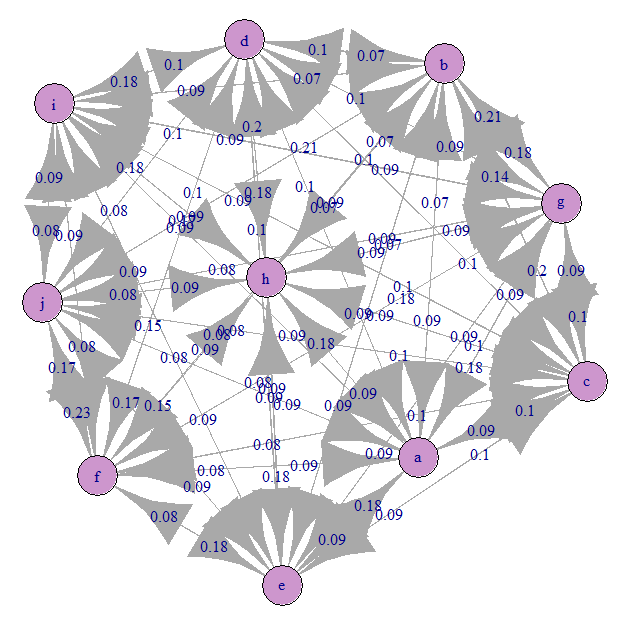
Semuanya kira-kira sama rata). Ini karena kami menentukan transisi yang dapat disempurnakan.

Dan sekarang adalah waktu untuk sihir!

 ## calculate pagerank ei <- eigen(A) as.numeric(ei$values[1]) pr <- as.numeric(ei$vectors[,1] / sum(ei$vectors[,1])) sum(pr) names(pr) <- node_names print(round(pr, 2)) 

Untuk matriks stokastik A, nilai eigen pertama harus sama dengan kesatuan, dan vektor eigen yang sesuai adalah vektor PageRank.

> cetak (bulat (pr, 2))
abcdefghij
0,09 0,11 0,09 0,10 0,10 0,11 0,10 0,11 0,08 0,11

Ini adalah vektor dari nilai-nilai PR - ini adalah vektor eigen yang dinormalisasi dari matriks transisi A yang sesuai dengan nilai eigen dari matriks ini sama dengan satu kesatuan - vektor eigen dominan.

Sekarang Anda dapat memberi peringkat elemen. Tetapi karena spesifik dari percobaan, mereka memiliki bobot yang sangat mirip.

Masalah dan solusinya menggunakan metode daya

Matriks transisi A mungkin tidak memenuhi kondisi stokastik.

Pertama, mungkin ada elemen yang tidak merujuk ke mana pun, yaitu, dengan tidak adanya umpan balik (mereka dapat merujuknya sendiri). Untuk grafik nyata yang besar, ini kemungkinan masalah. Ini berarti bahwa salah satu kolom dari matriks hanya akan memiliki nol. Dalam hal ini, solusi melalui vektor eigen tidak akan berfungsi.

Google memecahkan masalah ini dengan mengisi kolom dengan distribusi probabilitas seragam p = 1 / N. Di mana N adalah jumlah semua elemen.

 dim.1 <- dim(A)[1] A <- as.data.table(A) nul_cols <- apply(A, 2, function(x) sum(x) == 0) if( sum(nul_cols) > 0 ) { A[ , (colnames(A)[nul_cols]) := lapply(.SD, function(x) 1 / dim.1) , .SDcols = colnames(A)[nul_cols] ] } A <- as.matrix(A) 

Kedua, grafik dapat berisi elemen dengan umpan balik satu sama lain, tetapi tidak elemen yang tersisa dari grafik. Ini juga merupakan masalah yang tidak dapat diatasi untuk aljabar linier karena pelanggaran asumsi.

Ini diselesaikan dengan memperkenalkan konstanta yang disebut faktor Redaman, yang menunjukkan probabilitas a priori dari transisi dari elemen apa pun ke elemen lainnya, bahkan jika tidak ada hubungan fisik. Dengan kata lain, difusi dimungkinkan dalam kondisi apa pun.

 d = 0.15 #damping factor (to ensure algorithm convergence) M <- (1 - d) * A + d * (1 / dim.1 * matrix(1, nrow = dim.1, ncol = dim.1)) # google matrix 

Jika kita menerapkan transformasi ini ke matriks kita, maka itu lagi dapat diselesaikan melalui vektor eigen!

Ketiga, matriks klise mungkin tidak persegi, tetapi ini sangat penting! Saya tidak akan mengingat saat ini, karena saya percaya Anda sendiri yang akan mencari cara untuk memperbaikinya.

Tetapi ada metode yang lebih cepat dan lebih akurat, yang juga lebih ekonomis dalam memori (yang mungkin relevan untuk grafik besar): Metode daya.

 ## pagerank function (tested on example from tutorial) rm(pagerank_func) pagerank_func <- function( A #transition matrix , eps = 0.00001 #sufficiently small error , d = 0.15 #damping factor (to ensure algorithm convergence) ) { dim.1 <- dim(A)[1] A <- as.data.table(A) nul_cols <- apply(A, 2, function(x) sum(x) == 0) if( sum(nul_cols) > 0 ) { A[ , (colnames(A)[nul_cols]) := lapply(.SD, function(x) 1 / dim.1) , .SDcols = colnames(A)[nul_cols] ] } A <- as.matrix(A) M <- (1 - d) * A + d * (1 / dim.1 * matrix(1, nrow = dim.1, ncol = dim.1)) # google matrix rank = as.numeric(rep(1 / dim.1, dim.1)) ## iterate until convergence while( sum( (rank - M %*% rank) ^ 2 ) > eps ) { rank <- M %*% rank } return(rank) } pr2 <- pagerank_func(A) pr2=as.vector(pr2) names(pr2)=node_names 

Voila!

> cetak (bulat (pr, 2))
abcdefghij
0,09 0,11 0,09 0,10 0,10 0,11 0,10 0,11 0,08 0,11
> cetak (bulat (pr2, 2))
abcdefghij
0,09 0,11 0,09 0,10 0,10 0,11 0,10 0,11 0,08 0,11

Pada ini saya akan mengakhiri tutorial. Semoga bermanfaat.

Saya lupa mengatakan bahwa untuk membangun matriks transisi (probabilitas), Anda dapat menggunakan kesamaan teks, jumlah referensi, fakta tautan, dan metrik lain yang mengarah pada probabilitas semu atau probabilitas. Contoh yang agak menarik adalah rangking kalimat dalam teks pada matriks kesamaan kata bags tf-idf untuk menyorot kalimat yang merangkum seluruh teks. Mungkin ada penggunaan PR lainnya secara kreatif.

Saya sarankan Anda mencoba sendiri untuk bermain dengan matriks transisi dan pastikan Anda mendapatkan nilai PR yang keren, yang juga cukup mudah untuk ditafsirkan.

Jika Anda melihat ketidakakuratan atau kesalahan dengan saya - tunjukkan di komentar atau pesan, dan saya akan memperbaiki semuanya.

Semua kode dikompilasi di sini:


PS: seluruh ide ini juga mudah diimplementasikan dalam bahasa lain, setidaknya dengan Python, saya melakukan semuanya tanpa kesulitan.