Penguatan pembelajaran dalam: ping pixel pong mentah

Ini adalah artikel lama tertunda tentang Reinforcement Learning (RL). RL adalah topik keren!

Anda mungkin tahu bahwa komputer sekarang dapat secara otomatis belajar bermain game ATARI (dengan mendapatkan piksel game mentah di pintu masuk!). Mereka mengalahkan juara dunia dalam permainan Go , virtual berkaki empat belajar berlari dan melompat , dan robot belajar melakukan tugas manipulasi kompleks yang menantang pemrograman eksplisit. Ternyata semua pencapaian ini tidak lengkap tanpa RL. Saya juga tertarik pada RL selama setahun terakhir: Saya bekerja dengan buku Richard Sutton (sekitar Referensi: diganti) , membaca kursus David Silver , menghadiri kuliah John Schulman , menulis perpustakaan RL tentang Javascript , dan magang di DeepMind pada musim panas, bekerja dalam sebuah kelompok DeepRL, dan yang terbaru, dalam pengembangan OpenAI Gym , adalah toolkit RL baru. Jadi saya, tentu saja, telah berada di gelombang ini selama setidaknya satu tahun, tetapi masih belum repot-repot untuk menulis catatan tentang mengapa RL sangat penting, tentang apa, tentang bagaimana semua itu berkembang.


Contoh menggunakan Deep Q-Learning. Dari kiri ke kanan: jaringan saraf memainkan ATARI, jaringan saraf memainkan AlphaGo, robot melipat Lego, virtual berkaki empat berjalan di sekitar rintangan virtual.

Sangat menarik untuk merefleksikan sifat kemajuan terbaru dalam RL. Saya ingin mencatat empat faktor terpisah yang mempengaruhi perkembangan AI:

1. Kecepatan Komputasi (GPU, Perangkat Khusus ASIC, Hukum Moore)
2. Data yang memadai dalam bentuk yang dapat digunakan (mis. ImageNet)
3. Algoritma (penelitian dan gagasan, mis. Backprop, CNN, LSTM)
4. Infrastruktur (Linux, TCP / IP, Git, ROS, PR2, AWS, AMT, TensorFlow, dll.).

Sama seperti dalam visi komputer, kemajuan dalam RL bergerak ... meskipun tidak sebanyak yang terlihat. Sebagai contoh, dalam visi komputer, jaringan saraf AlexNet 2012 adalah peningkatan dalam dan lebar versi jaringan saraf ConvNets 1990-an. Demikian pula, ATARI Deep Q-Learning 2013 adalah implementasi dari algoritma Q-Learning standar yang dapat Anda temukan di buku klasik Richard Sutton 1998. Lebih lanjut, AlphaGo menggunakan teknik Gradient Kebijakan dan pencarian pohon Monte Carlo (MCTS) juga merupakan ide lama atau kombinasinya. Tentu saja, dibutuhkan banyak keterampilan dan kesabaran untuk membuatnya bekerja, dan banyak pengaturan rumit telah dikembangkan di atas algoritma lama. Namun dalam perkiraan pertama, pendorong utama kemajuan saat ini bukanlah algoritma dan ide baru, tetapi intensifikasi perhitungan, data yang cukup, dan infrastruktur yang matang.

Sekarang kembali ke RL. Banyak orang tidak percaya bahwa kita dapat mengajarkan komputer cara memainkan game ATARI pada tingkat manusia menggunakan piksel mentah dari awal dan menggunakan algoritma belajar mandiri yang sama. Pada saat yang sama, setiap kali saya merasakan celah - betapa ajaibnya hal itu, dan betapa sederhananya itu benar-benar ada di dalam.

Pendekatan dasar yang kami gunakan sebenarnya cukup bodoh. Meskipun demikian, saya ingin memperkenalkan Anda dengan teknik Policy Gradient (PG), pilihan default favorit kami untuk memecahkan masalah dengan RL saat ini. Anda mungkin penasaran mengapa, sebaliknya, saya tidak bisa membayangkan DQN, yang merupakan alternatif dan algoritma RL yang lebih dikenal yang juga digunakan dalam pelatihan ATARI . Ternyata meskipun Q-Learning diketahui, itu tidak begitu sempurna. Sebagian besar orang memilih untuk menggunakan Gradient Kebijakan, termasuk penulis artikel DQN asli, yang telah menunjukkan bahwa dengan penyempurnaan yang baik, Gradien Kebijakan berfungsi lebih baik daripada Q-Learning. PG lebih disukai karena eksplisit: ada kebijakan yang jelas dan pendekatan yang koheren yang secara langsung mengoptimalkan imbalan yang diharapkan. Sebagai contoh, kita akan belajar cara memainkan ATARI Pong: dari awal, dari piksel mentah melalui Gradien Kebijakan dengan jaringan saraf. Dan kami akan menempatkan semua ini dalam 130 baris Python. ( Tautan intisari ) Mari kita lihat bagaimana ini dilakukan.



Atas: Ping Pong. Bawah: Presentasi Ping-pong sebagai kasus khusus proses pengambilan keputusan Markov (MDP) : Setiap simpul grafik sesuai dengan keadaan tertentu permainan, dan ujung-ujungnya menentukan probabilitas transisi ke negara lain. Setiap tulang rusuk juga menentukan hadiahnya. Tujuannya adalah untuk menemukan jalur terbaik dari negara bagian mana pun untuk memaksimalkan hadiah

Bermain Ping Pong adalah contoh yang bagus dari tantangan RL. Dalam versi ATARI 2600 kita akan memainkan satu raket sendiri. Racket lain dikendalikan oleh algoritma bawaan. Kami harus memukul bola sehingga pemain lain tidak punya waktu untuk memukulnya. Semoga tidak perlu menjelaskan apa itu Ping Pong. Pada level rendah, gim ini berfungsi sebagai berikut: kami mendapatkan bingkai gambar - larik 210x160x3 byte, dan memutuskan apakah kami ingin menggerakkan raket ATAS atau BAWAH. Artinya, kita hanya punya dua pilihan untuk mengelola game. Setelah setiap pilihan, simulator game melakukan aksinya dan memberi kami hadiah: hadiah +1 jika bola melewati raket lawan, atau -1 jika kami melewatkan bola. Kalau tidak 0. Dan, tentu saja, tujuan kita adalah menggerakkan raket sehingga kita mendapatkan hadiah sebanyak mungkin.

Ketika mempertimbangkan solusi, ingatlah bahwa kami akan mencoba membuat beberapa asumsi tentang pong, karena itu tidak terlalu penting dalam praktik. Kami mempertimbangkan lebih banyak hal dalam tugas berskala besar, seperti memanipulasi robot, merakit, dan navigasi. Pong hanyalah sebuah test case mainan yang menyenangkan yang kami mainkan sementara kami memikirkan cara menulis sistem AI yang sangat umum yang suatu hari dapat melakukan tugas-tugas berguna yang sewenang-wenang.

Jaringan saraf sebagai kebijakan RL . Pertama, kita akan menentukan kebijakan apa yang diterapkan oleh pemain kami (atau "agen"). ((*) "Agen", "lingkungan" dan "kebijakan agen" adalah istilah standar dari teori RL). Fungsi kebijakan dalam kasus kami adalah jaringan saraf. Dia akan menerima keadaan permainan di pintu masuk dan di pintu keluar dia akan memutuskan apa yang harus dilakukan - naik atau turun. Sebagai blok perhitungan sederhana favorit kami, kami akan menggunakan jaringan saraf dua lapis yang mengambil piksel gambar mentah (total 100.800 angka (210 * 160 * 3)) dan menghasilkan angka tunggal yang menunjukkan kemungkinan memindahkan raket ke atas. Harap dicatat bahwa penggunaan kebijakan stokastik adalah standar, yang berarti bahwa kami hanya menghasilkan kemungkinan pergerakan ke atas. Untuk mendapatkan langkah yang sebenarnya, kami akan menggunakan probabilitas ini. Alasan untuk ini akan menjadi lebih jelas ketika kita berbicara tentang pelatihan.


Fungsi kebijakan kami terdiri dari jaringan saraf 2-lapisan yang sepenuhnya terhubung

Lebih khusus, anggaplah bahwa pada input kita mendapatkan vektor X, yang berisi satu set piksel pra-diproses. Maka kita harus menghitung menggunakan python \ numpy:

h = np.dot(W1, x) # compute hidden layer neuron activations h[h<0] = 0 # ReLU nonlinearity: threshold at zero logp = np.dot(W2, h) # compute log probability of going up p = 1.0 / (1.0 + np.exp(-logp)) # sigmoid function (gives probability of going up) 

Dalam fragmen ini, W1 dan W2 adalah dua matriks yang kami inisialisasi secara acak. Kami tidak menggunakan bias, karena kami ingin. Perhatikan bahwa pada akhirnya kami menggunakan non-linearitas dari sigmoid, yang mengurangi probabilitas output ke kisaran [0,1]. Secara intuitif, neuron dalam lapisan tersembunyi (yang bobotnya terletak di W1) dapat mendeteksi berbagai skenario permainan (misalnya, bola ada di atas dan raket kita ada di tengah), dan bobot di W2 kemudian dapat memutuskan apakah kita harus naik dalam setiap kasus atau turun. W1 dan W2 acak awal, tentu saja, pada awalnya akan menyebabkan kejang dan kejang pada pemain neuro kami, yang menyamakannya dengan autis bodoh pada kontrol pesawat terbang. Jadi satu-satunya tugas sekarang adalah menemukan W1 dan W2, yang mengarah ke permainan yang bagus!

Ada komentar tentang preprocessing piksel - idealnya, Anda perlu mentransfer setidaknya 2 frame ke jaringan saraf sehingga dapat mendeteksi gerakan. Tetapi untuk menyederhanakan situasi, kami akan menerapkan perbedaan dua frame. Artinya, kita akan mengurangi frame saat ini dan sebelumnya dan hanya kemudian menerapkan perbedaan pada input dari jaringan saraf.

Kedengarannya seperti sesuatu yang mustahil. Pada titik ini, saya ingin Anda menghargai betapa rumitnya masalah RL. Kami mendapatkan 100 800 angka (210x160x 3) dan mengirimkannya ke jaringan saraf kami yang menerapkan kebijakan pemain (yang, secara kebetulan, dengan mudah memasukkan sekitar satu juta parameter dalam matriks W1 dan W2). Misalkan kita pada suatu saat memutuskan untuk naik. Game simulator dapat menjawab bahwa kali ini kita akan mendapatkan 0 penghargaan dan memberi kita 100 800 nomor untuk frame berikutnya. Kami dapat mengulangi proses ini ratusan kali sebelum kami mendapatkan hadiah yang tidak nol! Misalnya, misalkan kita akhirnya mendapat hadiah +1. Ini luar biasa, tetapi bagaimana kita dapat mengatakan - apa yang menyebabkan ini? Apakah ini tindakan yang kami lakukan tadi? Atau mungkin 76 frame kembali? Atau mungkin ini pertama kali dikaitkan dengan bingkai 10, dan kemudian kami melakukan sesuatu yang benar dalam bingkai 90? Dan bagaimana kita mencari tahu - mana dari jutaan "pena" yang harus diputar untuk mencapai kesuksesan yang lebih besar di masa depan? Kami menyebutnya tugas menentukan koefisien kepercayaan pada tindakan tertentu. Dalam kasus khusus dengan pong, kita tahu bahwa kita mendapatkan +1 jika bola melewati lawan. Alasan sebenarnya adalah bahwa kami secara tidak sengaja menendang bola di sepanjang jalan yang baik beberapa frame ke belakang, dan setiap tindakan berikutnya yang kami lakukan tidak mempengaruhi sama sekali. Dengan kata lain, kita dihadapkan dengan masalah komputasi yang sangat kompleks, dan semuanya terlihat agak suram.

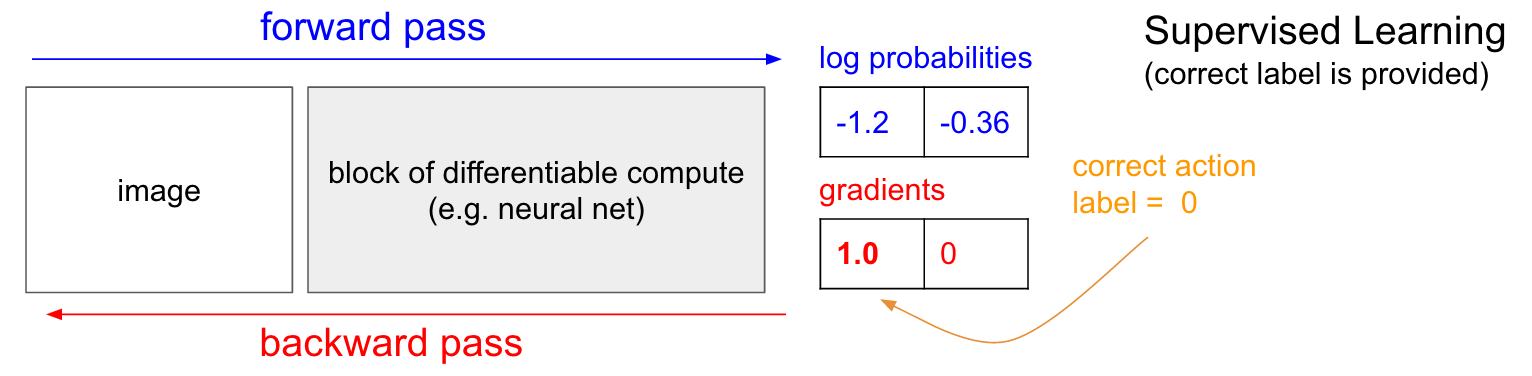
Pelatihan dengan seorang guru. Sebelum kita mempelajari gradien politik (PG), saya ingin mengingat secara singkat pengajaran dengan seorang guru, karena, seperti yang akan kita lihat, RL sangat mirip. Lihat grafik di bawah ini. Dalam pengajaran biasa dengan seorang guru, kami akan mentransfer gambar ke jaringan dan menerima pada keluaran beberapa probabilitas numerik untuk kelas-kelas. Sebagai contoh, dalam kasus kami, kami memiliki dua kelas: ATAS dan BAWAH. Saya menggunakan probabilitas logaritmik (-1.2, -0.36) daripada probabilitas dalam format 30% dan 70%, karena kami mengoptimalkan probabilitas logaritmik dari kelas (atau label) yang benar. Ini membuat perhitungan matematis lebih elegan dan setara dengan mengoptimalkan hanya probabilitas, karena logaritma bersifat monoton.

Dalam pelatihan dengan seorang guru, kita akan memiliki akses instan ke kelas (label) yang benar. Pada tahap pelatihan, mereka akan memberi tahu kami langkah tepat apa yang dibutuhkan saat ini (katakanlah UP, label 0), meskipun jaringan saraf mungkin berpikir berbeda. Oleh karena itu, kami menghitung gradien $$$\ nabla_ {W} \ log p (y = UP \ mid x)$ untuk mengubah pengaturan jaringan. Gradien ini hanya memberi tahu kita bagaimana kita harus mengubah masing-masing jutaan parameter kita sehingga jaringan sedikit lebih mungkin untuk memprediksi UP dalam situasi yang sama. Misalnya, satu dari sejuta parameter dalam jaringan dapat memiliki gradien -2.1, yang berarti bahwa jika kita meningkatkan parameter ini dengan nilai positif kecil (misalnya, 0,001), maka probabilitas logaritmik UP akan berkurang sebesar 2,1 * 0,001. (berkurang karena tanda negatif). Jika kami menerapkan gradien dan kemudian memperbarui parameter menggunakan algoritma backpropagation, maka, ya, jaringan kami akan memberikan probabilitas UP yang tinggi ketika melihat gambar yang sama atau sangat mirip di masa mendatang.



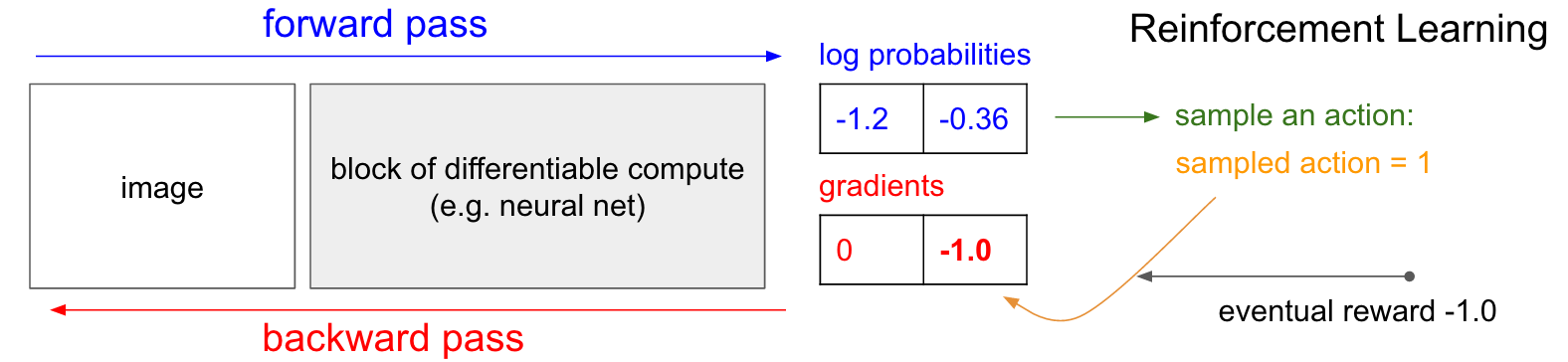
Gradien Politik (PG) . OK, tapi apa yang kita lakukan jika kita tidak memiliki label pelatihan penguatan yang tepat? Ini adalah solusi untuk PG (lihat diagram di bawah lagi). Jaringan saraf kami menghitung probabilitas kenaikan 30% (logprob -1.2) dan BAWAH sebesar 70% (logprob -0,36). Sekarang kami memilih dari distribusi ini dan menentukan tindakan apa yang akan kami lakukan. Misalnya, mereka memilih BAWAH dan mengirim tindakan ini ke simulator game. Pada titik ini, perhatikan satu fakta menarik: kita bisa segera menghitung dan menerapkan gradien untuk tindakan BAWAH, seperti yang kita lakukan dalam mengajar dengan seorang guru, dan dengan demikian membuat jaringan lebih mungkin untuk melakukan tindakan BAWAH di masa depan. Dengan demikian, kita dapat segera menghargai dan mengingat gradien ini. Tetapi masalahnya adalah bahwa saat ini kita belum tahu - apakah baik untuk BAWAH? Tetapi hal yang paling menarik adalah kita bisa menunggu sebentar dan menerapkan gradien nanti! Di Pong, kita bisa menunggu sampai akhir pertandingan, lalu mengambil hadiah yang kami terima (+1 jika kami menang, atau -1 jika kami kalah), dan memasukkannya sebagai faktor untuk gradien. Jadi, jika kita memperkenalkan -1 untuk probabilitas BAWAH dan melakukan propagasi balik, kami akan membangun kembali parameter jaringan sehingga kecil kemungkinannya untuk melakukan tindakan BAWAH di masa mendatang ketika menemukan gambar yang sama, karena penerapan tindakan ini menyebabkan kami kehilangan permainan. Artinya, kita perlu mengingat semua tindakan (input dan output dari jaringan saraf) dalam satu episode permainan dan, berdasarkan susunan ini, memutar jaringan saraf dengan cara yang hampir sama seperti dalam mengajar dengan seorang guru.



Dan hanya itu yang diperlukan: kita memiliki kebijakan stokastik yang memilih tindakan, dan kemudian di masa depan, tindakan yang pada akhirnya mengarah pada hasil yang baik didorong, dan tindakan yang mengarah pada hasil yang buruk tidak dianjurkan. Selain itu, hadiahnya seharusnya tidak menjadi +1 atau -1 jika kita akhirnya memenangkan permainan. Ini bisa menjadi nilai sewenang-wenang dari makna yang sama. Misalnya, jika semuanya bekerja dengan sangat baik, maka hadiahnya mungkin 10.0, yang kemudian kita gunakan sebagai gradien untuk memulai backpropagation backprop. Ini adalah keindahan jaringan saraf. Menggunakannya mungkin tampak seperti tipuan: Anda diperbolehkan memiliki 1 juta parameter yang dibangun dalam 1 teraflop perhitungan, dan Anda dapat membuat program belajar melakukan hal-hal yang sewenang-wenang dengan stochastic gradient descent (SGD). Seharusnya tidak bekerja, tetapi lucu bahwa kita hidup di alam semesta tempat ia bekerja.

Jika kami memainkan permainan papan sederhana, seperti catur, maka urutannya kurang lebih sama. Ada perbedaan nyata dari algoritma kliping minimax atau alpha-beta. Dalam algoritma ini, program terlihat beberapa langkah ke depan, mengetahui aturan permainan, dan menganalisis jutaan posisi. Dalam pendekatan RL, hanya gerakan yang benar-benar dibuat yang dianalisis. Pada saat yang sama, jaringan saraf tidak menantikan, karena tidak tahu apa-apa tentang aturan permainan.

Agar latihan secara detail. Kami membuat dan menginisialisasi jaringan saraf dengan beberapa W1, W2 dan memainkan 100 game pong (kami menyebutnya "run-in" politik, peluncuran kebijakan). Misalkan setiap permainan terdiri dari 200 frame, jadi secara total kami membuat 100 * 200 = 20.000 keputusan untuk naik atau turun. Dan untuk setiap solusi, kami tahu gradien yang memberi tahu kami bagaimana parameter harus berubah jika kami ingin mendorong atau melarang solusi ini dalam keadaan ini di masa mendatang. Yang tersisa sekarang adalah memberi label pada setiap keputusan yang kita buat sebagai baik atau buruk. Sebagai contoh, misalkan kita memenangkan 12 pertandingan dan kalah 88. Kami akan mengambil semua 200 * 12 = 2400 keputusan yang kami buat dalam permainan yang menang dan membuat pembaruan positif (mengisi gradien +1.0 untuk setiap tindakan, melakukan backprop, dan memperbarui parameter mendorong tindakan yang telah kami pilih dalam semua kondisi ini). Dan kami akan mengambil 200 * 88 = 17.600 keputusan lain yang kami buat dalam kekalahan dan membuat pembaruan negatif (tidak menyetujui apa yang kami lakukan). Dan hanya itu yang dibutuhkan. Jaringan sekarang akan lebih cenderung mengulangi tindakan yang berhasil, dan sedikit lebih mungkin mengulangi tindakan yang tidak berhasil. Sekarang kita memainkan 100 game lain dengan kebijakan baru yang sedikit ditingkatkan, dan kemudian mengulangi penerapan gradien.


Skema kartun dari 4 game. Setiap lingkaran hitam adalah semacam status permainan (tiga contoh status ditunjukkan di bawah), dan setiap panah adalah transisi yang ditandai dengan tindakan yang dipilih. Dalam hal ini, kami memenangkan 2 pertandingan dan kalah 2 pertandingan. Kami mengambil dua pertandingan yang kami menangi dan dengan ringan mendorong setiap tindakan yang kami lakukan dalam episode ini. Sebaliknya, kami juga akan mengambil dua pertandingan yang hilang dan sedikit mencegah setiap tindakan individu yang kami lakukan dalam episode ini.

Jika Anda merenungkan hal ini, Anda akan mulai menemukan beberapa sifat menyenangkan. Sebagai contoh, bagaimana jika kita melakukan tindakan yang baik dalam frame 50, menendang bola dengan benar, tetapi kemudian melewatkan bola di frame 150? Karena kami kalah dalam permainan, setiap aksi individu sekarang ditandai sebagai buruk, dan bukankah ini mencegah hit yang tepat pada frame 50? Anda benar - itu akan berlaku untuk pesta ini. Namun, ketika Anda mempertimbangkan proses dalam ribuan / jutaan game, eksekusi rebound yang tepat meningkatkan kemungkinan Anda untuk menang di masa depan. Rata-rata, Anda akan melihat pembaruan lebih positif daripada negatif untuk serangan raket yang tepat. Dan kebijakan implementasi jaringan saraf pada akhirnya akan menghasilkan reaksi yang tepat.

Pembaruan: 9 Desember 2016 adalah pandangan alternatif. Dalam penjelasan saya di atas, saya menggunakan istilah-istilah seperti "mendefinisikan gradien dan propagasi backprop back," yang merupakan teknik terampil yang pasti. Jika Anda terbiasa menulis kode backsprop backprop Anda sendiri atau menggunakan Torch, saat Anda dapat sepenuhnya mengontrol gradien. Namun, jika Anda terbiasa dengan Theano atau TensorFlow, Anda akan sedikit bingung karena kode backprop sepenuhnya otomatis dan sulit untuk disesuaikan. Dalam hal ini, pandangan alternatif berikut mungkin lebih produktif. Dalam mengajar dengan seorang guru, tujuan yang biasa adalah untuk memaksimalkan $$$\ sum_i \ log p (y_i \ mid x_i)$ dimana $$$x_i, y_i$ - contoh pelatihan (seperti gambar dan labelnya). Penerapan gradien ke fungsi kebijakan persis bertepatan dengan pelatihan dengan guru, tetapi dengan dua perbedaan kecil: 1) kami tidak memiliki label yang benar $$$y_i$ , oleh karena itu, sebagai "label palsu" kami menggunakan tindakan yang kami terima untuk memilih dari kebijakan ketika melihatnya $$$x_i$ , dan 2) Kami memperkenalkan koefisien kemanfaatan (keuntungan) lain untuk setiap tindakan. Jadi, pada akhirnya, kerugian kita sekarang terlihat seperti $$$\ sum_i A_i \ log p (y_i \ mid x_i)$ dimana $$$y_i$ - ini adalah tindakan yang kami lakukan dengan sampel, dan $$$A_i$ Adalah angka yang kita sebut koefisien kemanfaatan. Misalnya, dalam kasus pong, nilainya $$$A_i$ itu bisa 1.0 jika kita akhirnya memenangkan episode, dan -1.0 jika kita kalah. Ini memastikan bahwa kami memaksimalkan kemungkinan merekam tindakan yang mengarah pada hasil yang baik, dan meminimalkan kemungkinan merekam tindakan yang tidak. Dan tindakan netral sebagai akibat dari banyak seruan tidak akan secara khusus mempengaruhi fungsi politik. Dengan demikian, pembelajaran penguatan sama persis dengan belajar dengan guru, tetapi pada dataset yang selalu berubah (episode), dengan faktor tambahan.

Fitur kelayakan yang lebih canggih. Saya juga menjanjikan sedikit informasi. Sejauh ini, kami telah mengevaluasi kebenaran dari setiap tindakan individu berdasarkan pada apakah kami menang atau tidak. Dalam pengaturan RL yang lebih umum, kami akan menerima "hadiah bersyarat" $$$r_t$ untuk setiap langkah, tergantung pada jumlah langkah atau waktu. Salah satu opsi umum adalah dengan menggunakan koefisien diskon, sehingga "kemungkinan hadiah" pada diagram di atas akan menjadi $$$R_t = \ sum_ {k = 0} ^ {\ infty} \ gamma ^ k r_ {t + k}$ dimana $$$\ gamma$ Adalah angka dari 0 hingga 1, yang disebut koefisien diskon (misalnya, 0,99). Ungkapan tersebut mengatakan bahwa kekuatan yang kami anjurkan untuk bertindak adalah jumlah tertimbang dari semua hadiah, tetapi hadiah selanjutnya secara eksponensial kurang penting. Artinya, rantai tindakan pendek lebih baik didorong, dan ekor rantai tindakan panjang menjadi kurang penting. Dalam praktiknya, Anda juga perlu menormalkannya. Sebagai contoh, misalkan kita menghitung $$$R_t$ untuk semua 20.000 aksi dalam serangkaian 100 episode permainan. Ide yang sangat bagus adalah untuk menormalkan nilai-nilai ini (kurangi rata-rata, bagi dengan standar deviasi) sebelum kita menghubungkannya ke algoritma backprop. Karena itu, kami selalu mendorong dan mengecilkan setengah dari tindakan yang dilakukan. Ini mengurangi fluktuasi dan membuat kebijakan lebih konvergen. Studi yang lebih dalam dapat ditemukan di [ tautan ].

Berasal dari fungsi kebijakan. Saya juga ingin menjelaskan secara singkat bagaimana gradien diambil secara matematis. Kemiringan fungsi politik adalah kasus khusus dari teori yang lebih umum. Kasus umum adalah ketika kita memiliki ekspresi bentuk $$$E_ {x \ sim p (x \ mid \ theta)} [f (x)]$ , mis., harapan dari beberapa fungsi skalar $$$f (x)$ dengan beberapa distribusi parameternya $$$p (x; \ theta)$ diparameterisasi oleh beberapa vektor $$$\ theta$ . Lalu $$$f (x)$ akan menjadi fungsi hadiah kami (atau fungsi kemanfaatan dalam arti yang lebih umum), dan distribusi diskrit $$$p (x)$ akan menjadi kebijakan kami, yang sebenarnya memiliki formulir $$$p (a \ mid I)$ memberikan probabilitas tindakan untuk gambar $$$I$ . Kemudian kami tertarik pada bagaimana kami dapat menggeser distribusi p melalui parameternya $$$\ theta$ untuk memperbesar $$$f$ (mis. bagaimana kita mengubah pengaturan jaringan sehingga tindakan mendapatkan hadiah yang lebih tinggi). Kami punya ini:
$$$\ begin {align} \ nabla _ {\ theta} E_x [f (x)] & = \ nabla _ {\ theta} \ sum_x p (x) f (x) & \ text {definisi harapan} \\ & = \ sum_x \ nabla _ {\ theta} p (x) f (x) & \ text {swap penjumlahan dan gradien} \\ & = \ sum_x p (x) \ frac {\ nabla _ {\ theta} p (x)} {p (x)} f (x) & \ text {kalikan dan bagi dengan} p (x) \\ & = \ sum_x p (x) \ nabla _ {\ theta} \ log p (x) f (x) & \ text {gunakan fakta bahwa} \ nabla _ {\ theta} \ log (z) = \ frac {1} {z} \ nabla _ {\ theta} z \\ & = E_x [f (x) \ nabla _ {\ theta} \ log p (x)] & \ text {definisi harapan} \ end {align}$

Saya akan mencoba menjelaskan ini. Kami memiliki beberapa distribusi $$$p (x; \ theta)$ (Saya menggunakan singkatan $$$p (x)$ dari mana kita dapat memilih nilai tertentu. Sebagai contoh, itu mungkin distribusi Gaussian dari mana sampel generator nomor acak. Untuk setiap contoh, kami juga dapat menghitung fungsi estimasi $$$f$ , yang menurut contoh saat ini memberi kami beberapa perkiraan skalar. Persamaan yang dihasilkan memberitahu kita bagaimana kita harus menggeser distribusi melalui parameternya $$$\ theta$ jika kita ingin contoh tindakan lebih lanjut berdasarkan itu untuk mendapatkan tingkat yang lebih tinggi $$$f$ . Kami mengambil beberapa contoh tindakan $$$x$ dan penilaian mereka $$$f (x)$ , dan juga untuk setiap x, kami juga mengevaluasi istilah kedua $$$\ nabla _ {\ theta} \ log p (x; \ theta)$ . Apa pengali ini? Ini tepatnya vektor - gradien, yang memberi kita arah dalam ruang parameter, yang akan mengarah pada peningkatan probabilitas tindakan tertentu $$$x$ . Dengan kata lain, jika kita mendorong θ ke arah $$$\ nabla _ {\ theta} \ log p (x; \ theta)$ , kita akan melihat bahwa kemungkinan baru dari tindakan ini akan sedikit meningkat. Jika Anda melihat kembali formula, itu memberitahu kita bahwa kita harus mengambil arah ini dan mengalikan nilai skalar dengan itu $$$f (x)$ . Ini akan memastikan bahwa contoh tindakan dengan peringkat lebih tinggi (dalam kasus kami, hadiah) akan "menarik" lebih kuat daripada contoh dengan indikator yang lebih rendah, oleh karena itu, jika kami memperbarui berdasarkan beberapa sampel dari $$$p$ , kepadatan probabilitas akan bergeser ke arah poin permainan yang lebih tinggi, yang meningkatkan kemungkinan mendapatkan contoh tindakan dengan imbalan tinggi. Adalah penting bahwa gradien tidak diambil dari fungsi $$$f$ , karena secara umum dapat dibedakan dan tidak dapat diprediksi. A $$$p$ dibedakan oleh $$$\ theta$ . Yaitu $$$p$ adalah distribusi diskrit yang dapat disesuaikan terus-menerus, di mana Anda dapat menyesuaikan probabilitas tindakan individu. Kami juga menganggap itu $$$p$ dinormalisasi.



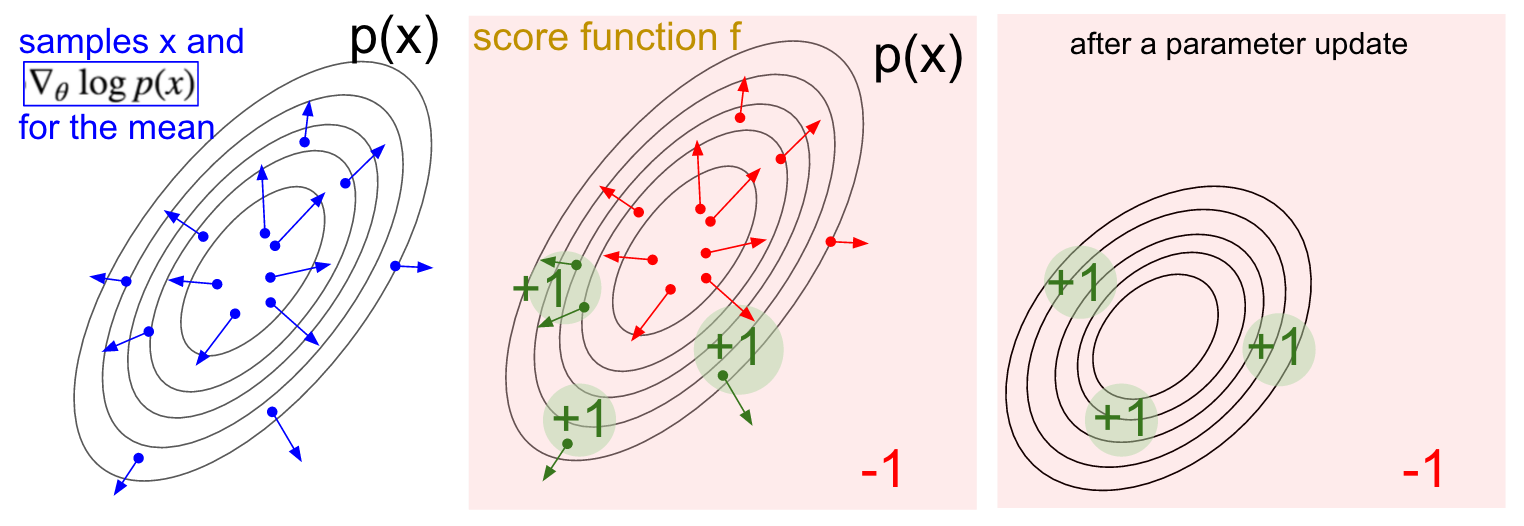Visualisasi gradien. Kiri: Distribusi Gauss dan beberapa contoh darinya (titik biru). Pada setiap titik biru, kami juga memplot gradien probabilitas logaritmik sehubungan dengan parameter rata-rata. Panah menunjukkan arah di mana nilai distribusi rata-rata harus digeser untuk meningkatkan kemungkinan tindakan contoh ini. Di tengah: Menambahkan beberapa fungsi evaluasi yang memberikan -1 di mana saja kecuali +1 di beberapa wilayah kecil (perhatikan bahwa ini bisa menjadi fungsi skalar yang sewenang-wenang dan tidak harus dibedakan). Panah sekarang diberi kode warna, karena karena perkalian kita akan rata-rata semua panah hijau dengan peringkat positif dan panah merah negatif. Kanan: setelah memperbarui parameter, panah hijau dan panah merah terbalik mendorong kita ke kiri dan ke bawah. Sampel dari distribusi ini sekarang akan memiliki peringkat yang diharapkan lebih tinggi, jika diinginkan.

Saya harap koneksi dengan RL jelas.Kebijakan kami memberi kami contoh tindakan, dan beberapa di antaranya bekerja lebih baik daripada yang lain (dinilai dari fungsi kemanfaatan). Cara untuk mengubah pengaturan kebijakan adalah dengan menjalankan, mengambil gradien dari tindakan yang dipilih, kalikan dengan peringkat dan tambahkan semua yang kami lakukan di atas. Untuk kesimpulan yang lebih menyeluruh, saya merekomendasikan kuliah oleh John Shulman.

Pelatihan Ya, kami telah mengembangkan prinsip-prinsip gradien fungsi politik. Saya menerapkan seluruh pendekatan dalam skrip Python 130-baris yang menggunakan emulator PAI ATAI 2600 siap pakai dari OpenAI Gym. Saya melatih jaringan saraf dua lapis dengan 200 neuron lapisan tersembunyi menggunakan algoritma RMSProp untuk serangkaian 10 episode (setiap episode, menurut aturan, terdiri dari beberapa pengundian bola dan episode tersebut terus mencetak skor 21). Saya tidak mengatur terlalu banyak parameter hiper dan bereksperimen di Macbook lambat saya, tetapi setelah latihan tiga hari saya mendapat kebijakan yang memainkan sedikit lebih baik daripada pemain built-in. Jumlah total episode sekitar 8.000, jadi algoritma memainkan sekitar 200.000 permainan pong, yang cukup banyak, dan menghasilkan total ~ 800 pembaruan untuk bobot. Jika saya berlatih GPU dengan ConvNets, maka dalam beberapa hari, saya bisa mencapai hasil yang bagus, dan jika saya mengoptimalkan hiperparameter, saya selalu bisa menang. Namun, saya tidak menghabiskan terlalu banyak waktu menghitung atau menyiapkan,jadi alih-alih kami mendapat Pong AI, yang menggambarkan ide-ide utama dan bekerja dengan sangat baik:


.

.Kita juga bisa melihat bobot yang diperoleh dari jaringan saraf. Berkat preprocessing, masing-masing input kami adalah gambar selisih 80x80 (frame saat ini dikurangi frame sebelumnya). Setiap neuron dari lapisan W1 terhubung ke lapisan tersembunyi W2 yang terdiri dari 200 neuron. Jumlah obligasi adalah 80 * 80 * 200. Mari kita coba menganalisis koneksi ini. Kami akan memilah-milah semua neuron dari lapisan W2 dan memvisualisasikan apa yang menyebabkan bobotnya. Dari skala yang mengarah ke satu neuron W2 dari neuron W1, kita akan membuat gambar 80x80. Di bawah ini adalah 40 gambar W2 (total 200). Piksel putih adalah bobot positif, dan hitam adalah negatif. Perhatikan bahwa beberapa neuron W2 disetel ke bola terbang yang disandikan dalam garis putus-putus. Dalam sebuah permainan, bola hanya bisa berada di satu tempat,karena itu, neuron-neuron ini multi-guna dan akan “menembak” jika bola berada di suatu tempat di dalam garis-garis ini. Pergantian hitam dan putih itu menarik, karena ketika bola bergerak di sepanjang lintasan, aktivitas neuron akan berfluktuasi seperti gelombang sinus. Dan karena ReLU, ia hanya akan "menembak" pada posisi tertentu. Ada banyak suara dalam gambar, yang akan lebih sedikit jika saya menggunakan regularisasi L2.



Apa yang tidak terjadi Jadi, kami belajar cara bermain pong pada gambar menggunakan gradien fungsi kebijakan, dan ini bekerja dengan cukup baik. Pendekatan ini adalah bentuk "saran dan verifikasi" yang aneh, di mana "tebakan" mengacu pada menjalankan kebijakan kami pada beberapa episode permainan, dan "memeriksa" mendorong tindakan yang mengarah pada hasil yang baik. Secara umum, ini mewakili level saat ini tentang bagaimana kita saat ini mendekati masalah pembelajaran yang diperkuat. Jika Anda memahami algoritma secara intuitif dan tahu cara kerjanya, Anda setidaknya harus sedikit kecewa. Secara khusus, kapan itu tidak berhasil?

Bandingkan ini dengan bagaimana seseorang dapat belajar bermain pong. Anda sendiri menunjukkan kepada mereka permainan dan mengatakan sesuatu seperti: "Anda mengontrol raket, dan Anda dapat memindahkannya ke atas dan ke bawah, dan tugas Anda adalah melempar bola melewati pemain lain yang dikendalikan oleh program bawaan," dan Anda siap untuk pergi. Harap perhatikan beberapa perbedaan:

• - , , , . RL , . , ( ), , . . , , , , , , , , .
  
• , ( , , , ..), ( «» « , , , - - . .). «» / . , , ( ) ( , ).
  
• — (brute force), , . . , , , . , «» , . , , .
  
• , , . , , . .
  

: : RL. , , . , . , 99% . , «» . : «», , - , - , - , , . « , ».

Saya juga ingin menekankan fakta bahwa, sebaliknya, dalam banyak permainan, gradien politik akan dengan mudah mengalahkan seseorang. Secara khusus, ini berlaku untuk permainan dengan hadiah yang sering, yang membutuhkan reaksi yang akurat dan cepat dan tanpa perencanaan jangka panjang. Korelasi jangka pendek antara imbalan dan tindakan dapat dengan mudah dilihat dengan pendekatan AM. Anda dapat melihat yang serupa di agen kami Pong. Dia mengembangkan strategi ketika dia hanya menunggu bola, dan kemudian bergerak cepat untuk menangkapnya hanya di tepi, itulah sebabnya bola memantul dengan kecepatan vertikal yang tinggi. Agen mendapatkan beberapa kemenangan berturut-turut, mengulangi strategi sederhana ini. Ada banyak permainan (Pinball, Breakout) di mana Deep Q-Learning menarik dan menginjak-injak seseorang ke dalam lumpur dengan tindakan sederhana dan tepat.

Setelah Anda memahami "trik" yang digunakan algoritma ini, Anda dapat memahami kekuatan dan kelemahannya. Secara khusus, algoritma ini jauh di belakang orang dalam membangun ide abstrak tentang game yang dapat digunakan orang untuk belajar cepat. Setelah komputer melihat susunan piksel dan memperhatikan kunci, pintu dan berpikir bahwa mungkin akan lebih baik untuk mengambil kunci dan sampai ke pintu. Saat ini tidak ada yang dekat dengan ini, dan mencoba untuk sampai ke sana adalah area penelitian aktif.

Komputasi yang tidak dapat dibedakan dalam jaringan saraf.Saya ingin menyebutkan aplikasi menarik lain dari gradien kebijakan yang tidak terkait game: memungkinkan kita untuk merancang dan melatih jaringan saraf menggunakan komponen yang melakukan (atau berinteraksi) dengan perhitungan yang tidak dapat dibedakan. Ide ini pertama kali diperkenalkan pada tahun 1992 oleh Williams . dan baru-baru ini dipopulerkan dalam model perhatian visual berulang.disebut "perhatian penuh" dalam konteks model yang memproses gambar dengan urutan penampilan sempit beresolusi rendah, mirip dengan cara mata kita memeriksa objek dengan visi pusat yang berjalan. Pada setiap iterasi, RNN akan menerima bagian kecil dari gambar dan memilih lokasi yang perlu dilihat lebih lanjut. Misalnya, RNN dapat melihat posisi (5.30), mendapatkan potongan kecil gambar, kemudian memutuskan untuk melihat (24, 50), dll. Ada bagian dari jaringan saraf yang memilih ke mana harus mencari lebih jauh, dan kemudian memeriksanya. Sayangnya, operasi ini tidak dapat dibedakan, karena, kami tidak tahu apa yang akan terjadi jika kami mengambil sampel di tempat lain. Dalam kasus yang lebih umum, pertimbangkan jaringan saraf yang memiliki beberapa input dan output:



Perhatikan bahwa sebagian besar panah biru dapat dibedakan seperti biasa, tetapi beberapa transformasi tampilan juga dapat mencakup operasi pilih yang tidak dibeda-bedakan, yang disorot dengan warna merah. Kita bisa langsung melalui panah biru di arah yang berlawanan, tetapi panah merah adalah ketergantungan di mana kita tidak bisa membalikkan menyebarkan backprop.

Kebijakan gradien untuk menyelamatkan! Mari kita pikirkan bagian dari jaringan yang melakukan pengambilan sampel yang dapat direpresentasikan sebagai fungsi kebijakan stokastik yang tertanam dalam jaringan saraf besar. Oleh karena itu, selama pelatihan, kami akan menghasilkan beberapa contoh (ditunjukkan oleh cabang di bawah), dan kemudian kami akan mendorong sampel yang pada akhirnya mengarah ke hasil yang baik (dalam hal ini, misalnya, diukur dengan kerugian di akhir). Dengan kata lain, kami akan melatih parameter yang termasuk dalam panah biru menggunakan backprop, seperti biasa, tetapi parameter yang termasuk dalam panah merah sekarang akan diperbarui secara independen dari umpan mundur menggunakan gradien kebijakan, mendorong sampel yang menghasilkan kerugian rendah. Ide ini juga baru-baru ini dibingkai dengan baik.Estimasi gradien menggunakan grafik perhitungan stokastik.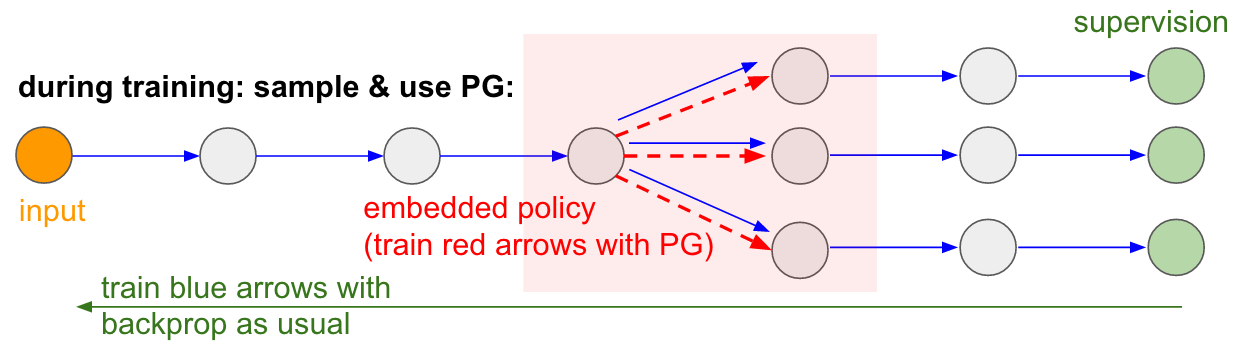



Input / output terlatih dalam memori akses acak. Anda juga akan menemukan ide ini di banyak artikel lainnya. Misalnya, Mesin Neural Turing memiliki pita memori yang dengannya mereka membaca dan menulis. Untuk melakukan operasi penulisan, Anda perlu melakukan sesuatu seperti m [i] = x, di mana i dan x diprediksi oleh jaringan saraf RNN. Namun, tidak ada sinyal yang memberi tahu kami apa yang akan terjadi pada fungsi kerugian jika kami menulis j! = I. Oleh karena itu, NTM dapat melakukan operasi baca dan tulis yang lunak. Dia memprediksi fungsi distribusi perhatian a, dan kemudian melakukan untuk semua i: m [i] = a [i] * x. Sekarang dapat dibedakan, tetapi kita harus membayar harga komputasi yang tinggi, memilah-milah semua sel.

Namun, kita dapat menggunakan gradien kebijakan untuk mengatasi masalah ini secara teoritis, seperti yang dilakukan di RL-NTM. Kami masih memperkirakan distribusi perhatian a, tetapi alih-alih pencarian lengkap, kami secara acak memilih tempat untuk menulis: i = sampel (a); m [i] = x. Selama pelatihan, kami bisa melakukan ini untuk satu set kecil saya dan, pada akhirnya, akan menemukan satu set yang akan bekerja lebih baik daripada yang lain. Keuntungan komputasi yang hebat adalah bahwa selama pengujian Anda dapat membaca / menulis dari satu sel. Namun, seperti yang ditunjukkan dalam dokumen, strategi ini sangat sulit untuk bekerja, karena Anda harus melalui banyak opsi dan hampir tidak sengaja pergi ke algoritma yang berfungsi. Saat ini, para peneliti sepakat bahwa PG berfungsi baik hanya ketika ada beberapa opsi terpisah, ketika Anda tidak perlu menyisir ruang pencarian yang besar.

Namun, dengan bantuan gradien kebijakan, dan dalam kasus di mana sejumlah besar data dan daya komputasi tersedia, pada prinsipnya kita dapat memimpikan banyak hal. Sebagai contoh, kita dapat mendesain jaringan saraf yang belajar berinteraksi dengan objek besar yang tidak dapat dibedakan, seperti kompiler Lateks. Misalnya, untuk char-rnn menghasilkan kode Lateks yang sudah jadi, atau sistem SLAM, atau pemecah LQR, atau yang lainnya. Atau, misalnya, kecerdasan super mungkin ingin belajar bagaimana berinteraksi dengan Internet melalui TCP / IP (yang juga tidak dapat dibedakan) untuk mengakses informasi yang diperlukan untuk menangkap dunia. Ini adalah contoh yang bagus.

Kesimpulan

Kami melihat bahwa gradien kebijakan adalah algoritma umum yang kuat, dan sebagai contoh, kami melatih agen ATARI Pong dari piksel mentah dari awal dalam 130 baris Python . Secara umum, algoritma yang sama dapat digunakan untuk melatih agen untuk game yang sewenang-wenang dan, semoga, suatu hari kita dapat menggunakannya untuk menyelesaikan masalah kontrol di dunia nyata. Sebagai kesimpulan, saya ingin menambahkan beberapa komentar:

Tentang pengembangan AI. Kami melihat bahwa algoritme bekerja dengan cara mencari brute force, di mana Anda pertama kali secara acak ragu dan harus menemukan situasi yang berguna setidaknya sekali, dan idealnya sering, sebelum fungsi kebijakan mengubah parameternya. Kami juga melihat bahwa seseorang mendekati solusi ini untuk masalah ini dengan cara yang sangat berbeda, yang menyerupai konstruksi cepat dari model abstrak. Karena model-model abstrak ini sangat sulit (jika bukan tidak mungkin) untuk dibayangkan secara eksplisit, ini juga merupakan alasan bahwa belakangan ini ada begitu banyak minat dalam model generatif dan induksi perangkat lunak.

Tentang penggunaan dalam robotika.Algoritma tidak berlaku di mana sulit untuk mendapatkan sejumlah besar penelitian. Misalnya, Anda dapat memiliki satu (atau beberapa) robot yang berinteraksi dengan dunia secara real time. Ini tidak cukup untuk aplikasi algoritma yang naif. Salah satu bidang pekerjaan yang dirancang untuk mengurangi masalah ini adalah gradien kebijakan deterministik . Alih-alih melakukan upaya nyata, pendekatan ini memperoleh informasi gradien dari jaringan saraf kedua (disebut kritik) yang memodelkan fungsi evaluasi. Pendekatan ini pada prinsipnya bisa efektif dengan tindakan berdimensi tinggi, di mana pengambilan sampel secara acak memberikan cakupan yang buruk. Pendekatan terkait lainnya adalah meningkatkan skala robot yang mulai kami lihat di Google Robot Farmatau mungkin bahkan pada Tesla S + dengan autopilot.

Ada juga pekerjaan yang mencoba membuat proses pencarian menjadi lebih tidak ada harapan dengan menambahkan kontrol tambahan. Misalnya, dalam banyak kasus praktis, Anda bisa mendapatkan arahan awal pengembangan langsung dari orang tersebut. Misalnya, AlphaGo pertama kali menggunakan pelatihan dengan guru untuk hanya memprediksi tindakan manusia (mis. Kontrol robot jarak jauh , magang , optimisasi lintasan , pencarian kebijakan penuh ). Dan kebijakan yang dihasilkan kemudian dikonfigurasi menggunakan PG untuk mencapai tujuan nyata - untuk memenangkan permainan.

Dalam beberapa kasus, mungkin ada lebih sedikit preset (misalnya, untuk mengontrol robot dari jarak jauh ), dan ada metode untuk menggunakan data pra-magang ini . Akhirnya, jika orang tidak memberikan data atau pengaturan tertentu, mereka juga dapat diperoleh dalam beberapa kasus dengan perhitungan menggunakan metode optimasi yang cukup mahal, misalnya, dengan mengoptimalkan lintasan dalam model dinamis yang dikenal (seperti F = ma dalam simulator fisik) atau dalam kasus ketika perkiraan model lokal dibuat (seperti yang terlihat dalam struktur yang sangat menjanjikan untuk pencarian kebijakan terkelola).

Tentang menggunakan PG dalam praktiknya.Saya ingin berbicara lebih banyak tentang RNN. Saya pikir itu mungkin tampak bahwa RNN ajaib dan secara otomatis menyelesaikan masalah yang berkaitan dengan urutan sewenang-wenang. Yang benar adalah, membuat model-model ini bekerja bisa rumit. Diperlukan perawatan dan pengalaman, serta mengetahui kapan metode yang lebih sederhana dapat membantu Anda 90%. Hal yang sama berlaku untuk gradien kebijakan. Mereka tidak bekerja secara otomatis begitu saja: Anda perlu memiliki banyak contoh, mereka dapat melatih selamanya, mereka sulit untuk di-debug ketika mereka tidak bekerja. Anda harus selalu mencoba menembak dari pistol kecil sebelum meraih Bazooka. Misalnya, dalam hal pelatihan penguatan, metode lintas-entropi (CEM) harus selalu diperiksa terlebih dahulu., pendekatan “tebak dan cek” stokastik sederhana yang diilhami oleh evolusi. Dan jika Anda bersikeras mencoba gradien kebijakan untuk tugas Anda, pastikan Anda tahu trik spesifiknya. Mulai sederhana dan gunakan opsi PG yang disebut TRPO , yang hampir selalu bekerja lebih baik dan lebih konsisten daripada PG klasik . Ide dasarnya adalah untuk menghindari memperbarui pengaturan yang mengubah kebijakan Anda terlalu banyak, karena penggunaan jarak Kulbak-Leibler antara kebijakan lama dan baru.

Itu saja!Saya harap saya memberi Anda gambaran tentang di mana kami berada bersama Reinforcement Learning, apa masalahnya, dan jika Anda ingin membantu mempromosikan RL, saya mengundang Anda untuk melakukan ini di OpenAI Gym kami :) Sampai jumpa di lain waktu!

---

Andrej Karpathy,
peneliti, pengembang, direktur departemen AI dan Tesla autopilot

Informasi tambahan:

Pembelajaran Mendalam tentang Kursus Fingers 2018
https://habr.com/en/post/414165/ Pembelajaran mendalam tentang Fingers

Kursus Terbuka 2019
https: // habr.com/ru/company/ods/blog/438940/

Fakultas Fisika NSU
http://www.phys.nsu.ru/