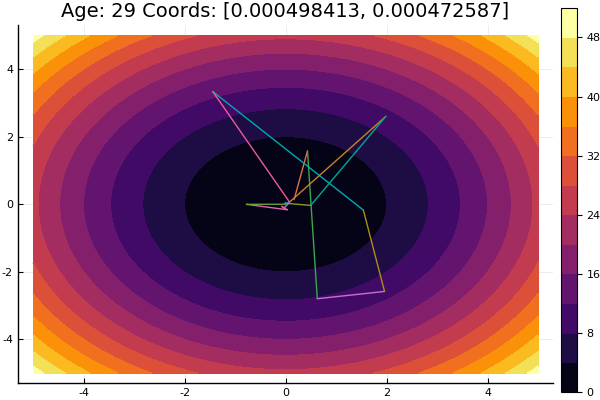
👩🏽 📅 🗯️ Julia dan metode penurunan koordinat 👍🏽 🎐 🙆🏼

Metode penurunan koordinat-bijaksana adalah salah satu metode paling sederhana dari optimasi multidimensi dan melakukan pekerjaan yang baik untuk menemukan fungsi minimum lokal dengan topografi yang relatif halus, sehingga lebih baik untuk mulai membiasakan diri dengan metode optimasi dari itu.

Pencarian ekstrem dilakukan ke arah sumbu koordinat, mis. selama proses pencarian, hanya satu koordinat yang diubah. Dengan demikian, masalah multidimensi berkurang menjadi satu dimensi.

Algoritma

Siklus pertama:

$x_1 = var$ , $x_2 = x_2 ^ 0$ , $x_3 = x_3 ^ 0$ ... $x_n = x_n ^ 0$ .
Mencari fungsi ekstrem $f (x_1)$ . Letakkan ekstrem fungsi pada titik $x_1 ^ 1$ .
$x_1 = x_1 ^ 1$ , $x_2 = var$ , $x_3 = x_3 ^ 0$ ... $x_n = x_n ^ 0$ . Fungsi ekstremum $f (x_2)$ sama dengan $x_2 ^ 1$
...
$x_1 = x_1 ^ 1$ , $x_2 = x_2 ^ 1$ , $x_3 = x_3 ^ 1$ ... $x_n = var$ .
Sebagai hasil dari melakukan n langkah, titik pendekatan baru untuk ekstrem ditemukan $(x_1 ^ 1, x_2 ^ 1, ..., x_n ^ 1)$ . Selanjutnya, kami memeriksa kriteria untuk akhir akun: jika terpenuhi, solusinya ditemukan, jika tidak kami melakukan siklus lain.

Persiapan

Periksa versi paket:

(v1.1) pkg> status Status `C:\Users\User\.julia\environments\v1.1\Project.toml` [336ed68f] CSV v0.4.3 [a93c6f00] DataFrames v0.17.1 [7073ff75] IJulia v1.16.0 [47be7bcc] ORCA v0.2.1 [58dd65bb] Plotly v0.2.0 [f0f68f2c] PlotlyJS v0.12.3 [91a5bcdd] Plots v0.23.0 [ce6b1742] RDatasets v0.6.1 [90137ffa] StaticArrays v0.10.2 [8bb1440f] DelimitedFiles [10745b16] Statistics

Kami mendefinisikan fungsi untuk menggambar garis permukaan atau level di mana akan lebih mudah untuk menyesuaikan batas-batas grafik:

 using Plots plotly() #   function plotter(plot_fun; low, up) Xs = range(low[1], stop = up[1], length = 80) Ys = range(low[2], stop = up[2], length = 80) Zs = [ fun([xy]) for x in Xs, y in Ys ]; plot_fun(Xs, Ys, Zs) xaxis!( (low[1], up[1]), low[1]:(up[1]-low[1])/5:up[1] ) #   yaxis!( (low[2], up[2]), low[2]:(up[2]-low[2])/5:up[2] ) end

Sebagai fungsi model, kami memilih paraboloid elips

 parabol(x) = sum(u->u*u, x) fun = parabol plotter(surface, low = [-1 -1], up = [1 1])

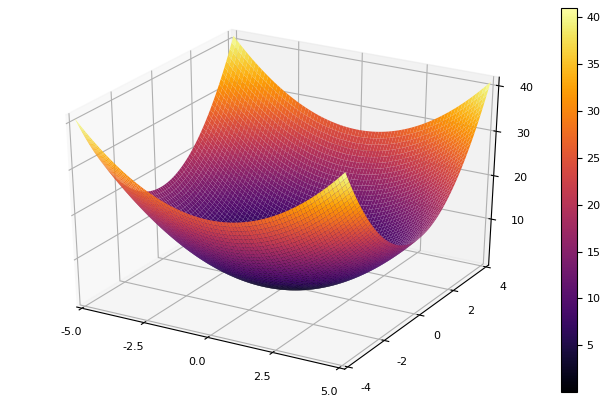
Koordinasikan keturunan

Kami menerapkan metode dalam fungsi yang mengambil nama metode optimasi satu dimensi, dimensi masalah, kesalahan yang diinginkan, perkiraan awal, dan batasan untuk menggambar garis level. Semua parameter diatur ke nilai default.

 function ofDescent(odm; ndimes = 2, ε = 1e-4, fit = [.5 .5], low = [-1 -1], up = [1 1]) k = 1 #      sumx = 0 sumz = 1 plotter(contour, low = low, up = up) #    x = [ fit[1] ] #     y = [ fit[2] ] #      while abs(sumz - sumx) > ε && k<80 fitz = copy(fit) for i = 1:ndimes odm(i, fit, ε) #    end push!(x, fit[1]) push!(y, fit[2]) sumx = sum(abs, fit ) sumz = sum(abs, fitz) #println("$k $fit") k += 1 end #     scatter!(x', y', legend = false, marker=(10, 0.5, :orange) );# , ,  p = title!("Age = $(size(x,1)) f(x,y) = $(fun(fit))") end

Selanjutnya, kita akan mencoba berbagai metode optimasi satu dimensi.

Metode Newton

x_{n + 1} = x_{n} - f r a c f (x_{n}) f^{'} (x_{n})

$x_ {n + 1} = x_n - \ frac {f (x_n)} {f '(x_n)}$

Gagasan metode ini sederhana seperti implementasinya

 #  dfun = (x, i) -> i == 1 ? 2x[1] + x[2]*x[2] : 2x[2] + x[1]*x[1] function newton2(i, fit, ϵ) k = 1 oldfit = Inf while ( abs(fit[i] - oldfit) > ϵ && k<50 ) oldfit = fit[i] tryfit = fun(fit) / dfun(fit, i) fit[i] -= tryfit println(" $k $fit") k+=1 end end ofDescent(newton2, fit = [9.1 9.1], low = [-4 -4], up = [13 13])

Newton cukup menuntut pada perkiraan awal, dan tanpa batasan pada langkah-langkah, ia dapat dengan mudah naik ke jarak yang tidak diketahui. Perhitungan turunan diinginkan, tetapi variasi kecil dapat ditiadakan. Kami memodifikasi fungsi kami:

 function newton(i, fit, ϵ) k = 1 oldfit = Inf x = [] y = [] push!(x, fit[1]) push!(y, fit[2]) while ( abs(oldfit - fit[i]) > ϵ && k<50 ) fx = fun(fit) oldfit = fit[i] fit[i] += 0.01 dfx = fun(fit) fit[i] -= 0.01 tryfit = fx*0.01 / (dfx-fx) #        if( abs(tryfit) > abs(fit[i])*10 ) push!(x, fit[1]) push!(y, fit[2]) break end fit[i] -= tryfit #println(" $k $fit") push!(x, fit[1]) push!(y, fit[2]) k+=1 end #  - -   plot!(x, y, w = 3, legend = false, marker = :rect ) end ofDescent(newton, fit = [9.1 9.1], low = [-4 -4], up = [13 13])

Interpolasi parabola terbalik

Suatu metode yang tidak memerlukan pengetahuan tentang turunan dan memiliki konvergensi yang baik

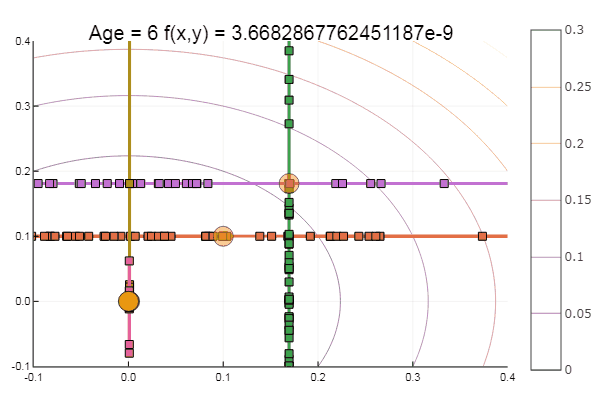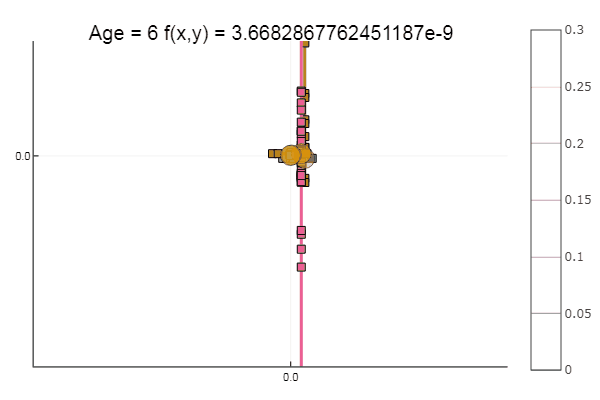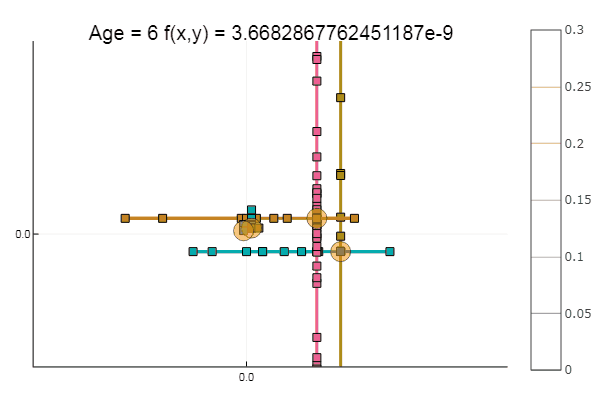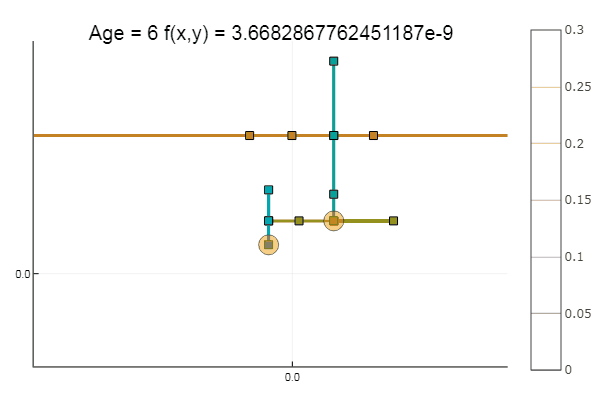
 function ipi(i, fit, ϵ) # inverse parabolic interpolation n = 0 xn2 = copy(fit) xn1 = copy(fit) xn = copy(fit) xnp = zeros( length(fit) ) xy = copy(fit) xn2[i] = fit[i] - 0.15 xn[i] = fit[i] + 0.15 fn2 = fun(xn2) fn1 = fun(xn1) while abs(xn[i] - xn1[i]) > ϵ && n<80 fn = fun(xn) a = fn1*fn / ( (fn2-fn1)*(fn2-fn ) ) b = fn2*fn / ( (fn1-fn2)*(fn1-fn ) ) c = fn2*fn1 / ( (fn -fn2)*(fn -fn1) ) xnp[i] = a*xn2[i] + b*xn1[i] + c*xn[i] xn2[i] = xn1[i] xn1[i] = xn[i] xn[i] = xnp[i] fn2 = fn1 fn1 = fn n += 1 println(" $n $xn $xn1") xy = [xy; xn] end fit[i] = xnp[i] plot!(xy[:,1], xy[:,2], w = 3, legend = false, marker = :rect ) end ofDescent(ipi, fit = [0.1 0.1], low = [-.1 -.1], up = [.4 .4])

Jika kita memperparah perkiraan awal, metode ini akan mulai membutuhkan sejumlah besar langkah untuk setiap era penurunan koordinat. Dalam hal ini, saudaranya menang

Interpolasi Parabola Sekuensial

Ini juga membutuhkan tiga titik awal , tetapi pada banyak fungsi tes ini menunjukkan hasil yang lebih memuaskan.

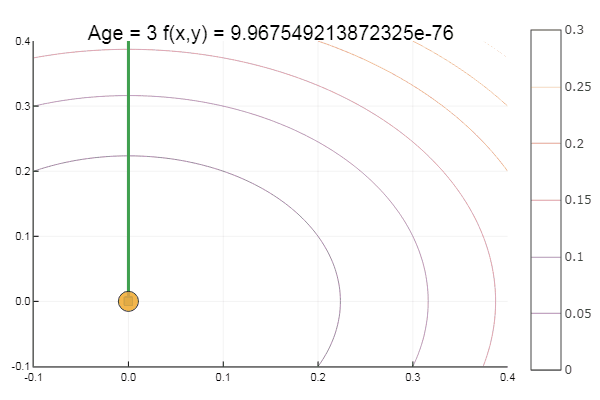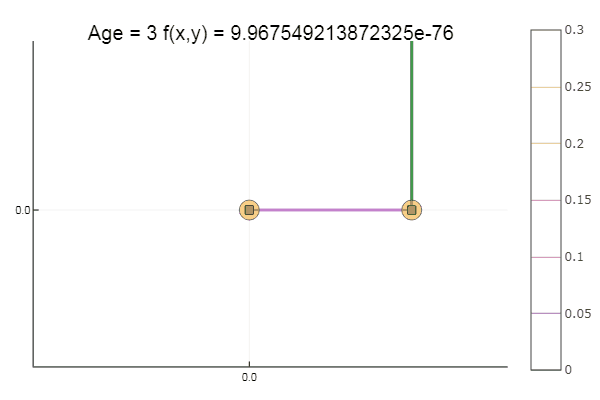
 function spi(i, fit, ϵ) # sequential parabolic interpolation n = 0 xn2 = copy(fit) xn1 = copy(fit) xn = copy(fit) xnp = zeros( length(fit) ) xy = copy(fit) xn2[i] = fit[i] - 0.01 xn[i] = fit[i] + 0.01 fn2 = fun(xn2) fn1 = fun(xn1) while abs(xn[i] - xn1[i]) > ϵ && n<200 fn = fun(xn) v0 = xn1[i] - xn2[i] v1 = xn[i] - xn2[i] v2 = xn[i] - xn1[i] s0 = xn1[i]*xn1[i] - xn2[i]*xn2[i] s1 = xn[i] *xn[i] - xn2[i]*xn2[i] s2 = xn[i] *xn[i] - xn1[i]*xn1[i] xnp[i] = 0.5(fn2*s2 - fn1*s1 + fn*s0) / (fn2*v2 - fn1*v1 + fn*v0) xn2[i] = xn1[i] xn1[i] = xn[i] xn[i] = xnp[i] fn2 = fn1 fn1 = fn n += 1 println(" $n $xn $xn1") xy = [xy; xn] end fit[i] = xnp[i] plot!(xy[:,1], xy[:,2], w = 3, legend = false, marker = :rect ) end ofDescent(spi, fit = [16.1 16.1], low = [-.1 -.1], up = [.4 .4])

Melangkah keluar dari titik awal yang sangat buruk terjadi dalam tiga langkah! Bagus ... Tetapi semua metode memiliki kelemahan - mereka bertemu ke minimum lokal. Sekarang mari kita ambil fungsi Ackley untuk penelitian

f (x, y) = - 20 e x p k i r i [- 0.2 s q r t 0, 5 k i r i (x^{2} + y^{2} k a n a n) k a n a n] - e x p k i r i [0, 5 k i r i (c o s 2 p i x + c o s 2 p i y k a n a n) k a n a n] + e + 20

$f (x, y) = - 20 \ exp \ kiri [-0.2 {\ sqrt {0,5 \ kiri (x ^ {2} + y ^ {2} \ kanan)}} \ kanan] - \ exp \ kiri [ 0,5 \ kiri (\ cos 2 \ pi x + \ cos 2 \ pi y \ kanan) \ kanan] + e + 20$

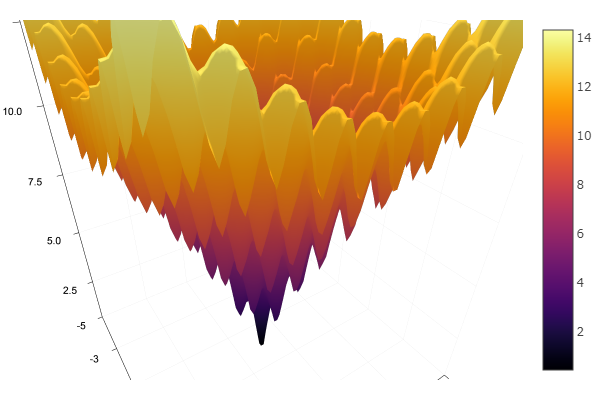
 ekly(x) = -20exp(-0.2sqrt(0.5(x[1]*x[1]+x[2]*x[2]))) - exp(0.5(cospi(2x[1])+cospi(2x[2]))) + 20 + ℯ # f(0,0) = 0, x_i ∈ [-5,5] fun = ekly plotter(surface, low = [-5 -5], up = [5 5])

 ofDescent(spi, fit = [1.4 1.4], low = [-.1 -.1], up = [2.4 2.4])

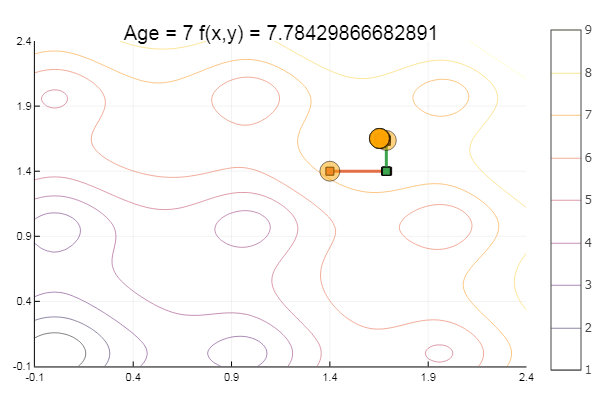
Metode Rasio Emas

Teori Meskipun implementasinya rumit, metode ini terkadang menunjukkan dirinya dengan baik dengan melompati minima lokal

 function interval(i, fit, st) d = 0. ab = zeros(2) fitc = copy(fit) ab[1] = fitc[i] Fa = fun(fitc) fitc[i] -= st Fdx = fun(fitc) fitc[i] += st if Fdx < Fa st = -st end fitc[i] += st ab[2] = fitc[i] Fb = fun(fitc) while Fb < Fa d = ab[1] ab[1] = ab[2] Fa = Fb fitc[i] += st ab[2] = fitc[i] Fb = fun(fitc) # println("----", Fb, " ", Fa) end if st < 0 c = ab[2] ab[2] = d d = c end ab[1] = d ab end function goldsection(i, fit, ϵ) ϕ = Base.MathConstants.golden ab = interval(i, fit, 0.01) α = ϕ*ab[1] + (1-ϕ)*ab[2] β = ϕ*ab[2] + (1-ϕ)*ab[1] fit[i] = α Fa = fun(fit) fit[i] = β Fb = fun(fit) while abs(ab[2] - ab[1]) > ϕ if Fa < Fb ab[2] = β β = α Fb = Fa α = ϕ*ab[1] + (1-ϕ)*ab[2] fit[i] = α Fa = fun(fit) else ab[1] = α α = β Fa = Fb β = ϕ*ab[2] + (1-ϕ)*ab[1] fit[i] = β Fb = fun(fit) end println(">>>", i, ab) plot!(ab, w = 1, legend = false, marker = :rect ) end fit[i] = 0.5(ab[1] + ab[2]) end ofDescent(goldsection, fit = [1.4 1.4], low = [-.1 -.1], up = [1. 1.])

Itu semua dengan keturunan koordinat. Algoritma dari metode yang disajikan cukup sederhana, jadi menerapkannya dalam bahasa pilihan Anda tidak sulit. Di masa depan, Anda dapat mempertimbangkan alat bawaan dari bahasa Julia , tetapi untuk sekarang, Anda ingin menyentuh segalanya, sehingga untuk berbicara, dengan tangan Anda, pertimbangkan metode yang lebih rumit dan lebih efisien, maka Anda dapat pergi ke optimasi global, secara bersamaan membandingkan dengan implementasi dalam bahasa lain.

Sastra

Zaitsev V.V. Metode numerik untuk fisikawan. Persamaan dan optimisasi nonlinier: tutorial. - Samara, 2005 - 86-an.
Ivanov A.V. Metode komputer untuk mengoptimalkan sistem optik. Panduan belajar. –SPb: SPbSU ITMO, 2010 - 114s.
Popova T. M. Metode optimasi multidimensi: pedoman dan tugas untuk pekerjaan laboratorium dalam disiplin "Metode optimasi" untuk siswa dari arah "Matematika Terapan" / comp. T. M. Popova. - Khabarovsk: Rumah Penerbitan Pasifik. negara University, 2012 .--44 hal.

Julia dan metode penurunan koordinat