Berkenalan dengan jaringan saraf paling sederhana dan penerapannya selangkah demi selangkah

Suatu ketika saya menemukan sebuah buku berjudul "Buat Jaringan Saraf Anda" , yang ditulis oleh Tarik Rashid . Tidak seperti banyak buku lain di jaringan saraf, dalam hal ini semuanya disajikan dalam bahasa yang sederhana, dengan cukup banyak contoh dan kiat

Terinspirasi oleh buku ini, saya ingin memeriksanya selangkah demi selangkah - yaitu, bagian praktisnya - menulis kode untuk jaringan saraf sederhana .
Artikel ini ditujukan bagi mereka yang ingin terlibat dalam jaringan saraf dan pembelajaran mesin, tetapi sejauh ini mengalami kesulitan memahami bidang sains yang menakjubkan ini. Kerangka paling sederhana dari kode jaringan syaraf akan dijelaskan di bawah ini, sehingga banyak yang memahami prinsip konstruksi dan interaksi sederhana dari semua jaringan syaraf ini.




Teori tentang pembelajaran mesin dan jaringan saraf pada Habré sudah cukup. Tetapi jika seseorang membutuhkannya, saya akan meninggalkan beberapa tautan di akhir artikel. Dan sekarang, kita akan mulai menulis kode secara langsung, dan kita akan menulis dengan Python , saya sarankan menggunakan Jupyter-Notebook saat menulis kode

Langkah 1. Inisialisasi Jaringan

Pertama, tentu saja, kita perlu menginisialisasi semua komponen aktif dari jaringan kita

# numpy —    Python,        import numpy #  scipy.special , -scipy    , ,  ,      ,       ,   - " " import scipy.special #,      import matplotlib.pyplot #     class neuralNetwork: #     def __init__(self, inputnodes, hiddennodes, outputnodes, learningrate): #     ,   ,   ,  ) #     ,  ,   self.inodes = inputnodes self.hnodes = hiddennodes self.onodes = outputnodes #    , wih -       ,    who-       self.wih = numpy.random.rand(self.hnodes, self.inodes) self.who = numpy.random.rand(self.onodes, self.hnodes) #   -  ,  ,  ,    ,     ,     ,  ,  ,   self.lr = learningrate #  -   self.activation_function = lambda x: scipy.special.expit(x) 

Sigmoid

Fungsi ini milik kelas fungsi kontinu, mengambil angka real arbitrary (mis., Tidak harus bilangan bulat) pada input, dan memberikan bilangan real dalam kisaran dari 0 hingga 1 pada output .

Khususnya, bilangan negatif besar (modulo) berubah menjadi nol , dan bilangan positif besar berubah menjadi satu .

Keluarannya ditafsirkan dengan baik sebagai tingkat aktivasi neuron: dari tidak adanya aktivasi (0) hingga aktivasi penuh jenuh (1).

Sigmoid diekspresikan oleh rumus:



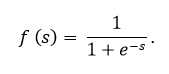
Grafik fungsi sigmoid sesuai dengan gambar di bawah ini:



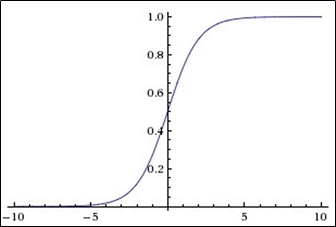
Fungsi sigmoid adalah:

• terus menerus
• meningkat secara monoton;
• terdiferensiasi.

Dalam kode ini, sigmoid hadir, seperti yang Anda lihat, dengan nama expit (x)

Sedikit tentang bagaimana sebuah node terlihat dalam jaringan saraf

Gambar menunjukkan paling banyak simpul itu, hanya saja biasanya disajikan dalam bentuk lingkaran, bukan persegi panjang. Seperti yang kita lihat, di dalam persegi panjang (baik, atau lingkaran) - ini semua abstrak, ada 2 fungsi:

Fungsi 1 terlibat dalam kenyataan bahwa ia menerima semua input, dengan mempertimbangkan bobot, data, dan kadang-kadang bahkan dengan mempertimbangkan neuron perpindahan (neuron khusus yang hanya memungkinkan grafik untuk bergerak, dan tidak bercampur menjadi satu tumpukan jelek, itu saja)

Fungsi 2 mengambil sebagai parameter nilai yang sama dengan fungsi pertama dijumlahkan, dan fungsi kedua ini disebut fungsi aktivasi. Dalam kasus kami, sebuah sigmoid

Kami melanjutkan :

Bagian 2. Pelatihan Jaringan Saraf Tiruan

 def train(self, inputs_list, targets_list): #       inputs = numpy.array(inputs_list, ndmin=2).T #     input targets = numpy.array(targets_list, ndmin=2).T #  targets #      hidden_inputs = numpy.dot(self.wih, inputs) #  ,       .    ,       hidden_inputs (1 ),        -   (2 ) hidden_outputs = self.activation_function(hidden_inputs) #    ()  final_inputs = numpy.dot(self.who, hidden_outputs) #  ,     final_outputs = self.activation_function(final_inputs) #   ( - ) output_errors = targets - final_outputs #      ,    <b>  </b>,   <b>       </b>(      ) hidden_errors = numpy.dot(self.who.T, output_errors) #        ( ,      ) self.who += self.lr * numpy.dot((output_errors * final_outputs * (1.0 - final_outputs)), numpy.transpose(hidden_outputs)) #       (       ) self.wih += self.lr * numpy.dot((hidden_errors * hidden_outputs * (1.0 - hidden_outputs)), numpy.transpose(inputs)) 

Dan sekarang kita mendekati akhir

Bagian 3. Interogasi jaringan saraf

 #  ,      def query(self, inputs_list): #         inputs = numpy.array(inputs_list, ndmin=2).T #      hidden_inputs = numpy.dot(self.wih, inputs) #  ,     hidden_outputs = self.activation_function(hidden_inputs) #      final_inputs = numpy.dot(self.who, hidden_outputs) #     ,     final_outputs = self.activation_function(final_inputs) return final_outputs 

Kami membawanya sampai akhir

 #     ,  ,  (  <b></b>-    , ,   input_nodes = 3 hidden_nodes = 3 output_nodes = 3 #    -   , ... 0.3! learning_rate = 0.3 #   (n    neuralNetwork ,      __init__ ,        n = neuralNetwork(input_nodes,hidden_nodes,output_nodes, learning_rate) 

PS

Di atas disajikan model komputasi jaringan saraf yang paling sederhana. Tetapi tidak ada aplikasi spesifik yang ditampilkan.

Jika mau, Anda dapat melangkah lebih jauh dengan menambahkan kemampuan mengenali teks tulisan tangan dalam kode MNIST , untuk ini Anda dapat sepenuhnya mengetahui (dan bersenang-senang) dengan file jupyter ini, tugas saya adalah mendemonstrasikan kode dan, jika mungkin, mengunyah jaringan dan untuk apa jawabannya

PPS

Di bawah ini Anda akan menemukan tautan yang berguna:

1. Tautan ke Github Tarik ->
2. bukunya ->
3.Machine Learning Theory ->
4.Machine Learning Theory ->
5.Machine Learning Theory ->