Jika Anda belum membaca artikel pertama saya tentang topik ini, saya menyarankan Anda untuk memulainya.
Karena saya menyebutkan sikap tertentu, meskipun sangat tidak langsung, terhadap matematikawan finansial, izinkan saya mengembangkan topik sampai pada titik absurditas berdasarkan pada bagaimana ia dikembangkan dalam Risk Analytics. Saat menghitung harga suatu opsi, mereka sering mempertimbangkan sensitivitas harga ini terhadap serangkaian parameter. Misalnya, bagaimana harga opsi akan berubah ketika harga saham yang mengeluarkan opsi berubah, atau ketika volatilitas harga saham, atau tingkat perubahan Bank Sentral, dll.
Kami mungkin tertarik pada bagaimana probabilitas memenangkan suatu game berubah ketika probabilitas untuk memenangkan poin berubah. Bahkan, kami ingin menghitung turunan dari yang pertama ke yang kedua. Pendekatan paling sederhana adalah dengan mengevaluasinya dengan mata dari grafik. Dapat dilihat bahwa maksimum dicapai dalam situasi 50:50. Jika peluang memenangkan poin berubah dari 0,45 menjadi 0,55, probabilitas memenangkan bulutangkis meningkat dari 0,26 menjadi 0,74, yaitu 0,48. Perkiraan kasar memberikan turunan di wilayah 5. Yaitu, jika Anda tumbuh hingga 0,51 (yaitu 51%) dengan peluang yang sama, peningkatan kemungkinan memenangkan permainan akan menjadi sekitar 0,05 (atau 5%). Demikian pula, Anda dapat menghitung turunannya di titik lain mana saja pada grafik.
Di bidang keuangan, pendekatan "bump and run" biasanya digunakan, yaitu, mereka mengubah parameter dengan jumlah kecil dan menghitung harga opsi baru dan turunannya. Setelah bertindak dengan cara yang sama, saya mengutip data yang tepat pada grafik (saya mengambil perubahan dengan persentase, sedikit kasar, tetapi dapat diterima dalam situasi ini). Untuk kejelasan yang lebih besar, ia menambahkan game hingga 5 dan 31 poin. Ngomong-ngomong, memotret dalam biathlon dapat dianggap sebagai pesta hingga 5. Ini bukan analogi absolut, karena jumlah total pemotretan ditetapkan. Tetapi metode solusinya hampir sama.
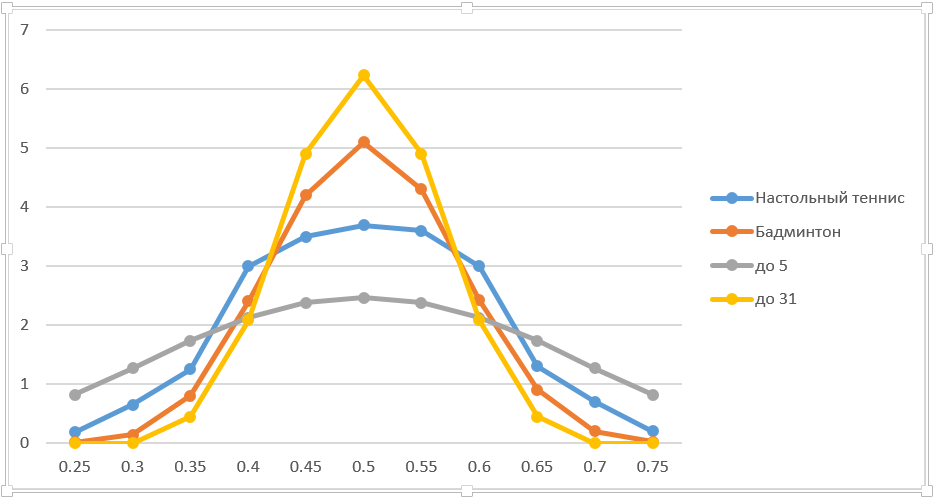
Jelas, semakin lama batch, semakin tinggi turunannya pada 50:50. Jika panjang pesta cenderung tak terbatas, kemenangan seorang pemain dengan bahkan keuntungan minimal praktis dijamin. Lebar kurva menurun sesuai dengan itu. Secara umum, kesimpulannya cukup jelas.
Anda dapat menghitung sensitivitas terhadap pelepasan satu titik tanpa disengaja. Misalnya, masukkan ke dalam jaring. Berapa satu slip yang mempengaruhi hasil permainan? Bahkan, ini adalah pengurangan skor kemenangan untuk lawan dengan satu poin. Grafik di bawah ini mencerminkan situasi ini. Secara alami, dalam tenis meja lebih penting kehilangan poin daripada di bulutangkis. Dengan kekuatan yang sama, probabilitas hasil pertandingan turun sebanyak mungkin - dari 0,5 menjadi 0,41. Perhatikan asimetri kurva (tidak seperti kebanyakan kurva lainnya). Ini bukan kebetulan. Faktanya adalah bahwa keseimbangan bergeser dari 50:50 ke probabilitas yang lebih tinggi untuk memenangkan poin, karena poin yang hilang memperburuk peluang pemain.
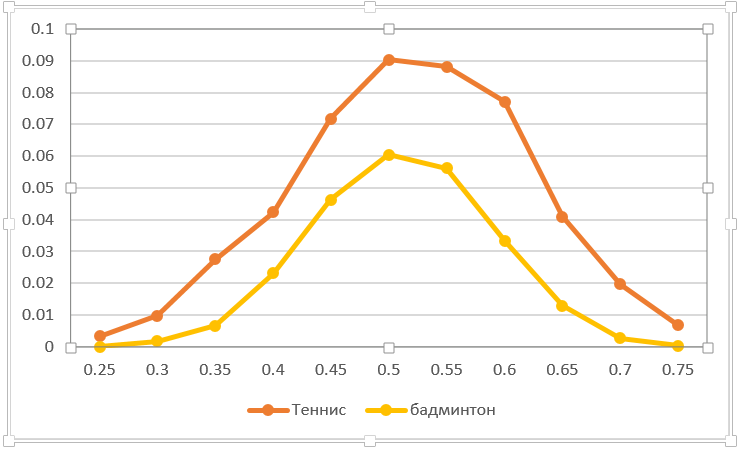
Mari kita letakkan pengalaman menarik lainnya. Bayangkan bahwa salah satu pemain dapat berkonsentrasi dan bermain 3 poin di atas rata-rata (p1 + delta). Misalkan setelah ini pelurusan akan kembali ke aslinya (ke rata-rata yang diharapkan tanpa memperhitungkan "lonjakan kekuatan"). Jelas bahwa kemungkinan menang akan meningkat. Pertanyaannya adalah, apakah penting untuk berkonsentrasi - di awal atau di akhir permainan? Saya mengusulkan untuk membuat asumsi sebelum membaca lebih lanjut.
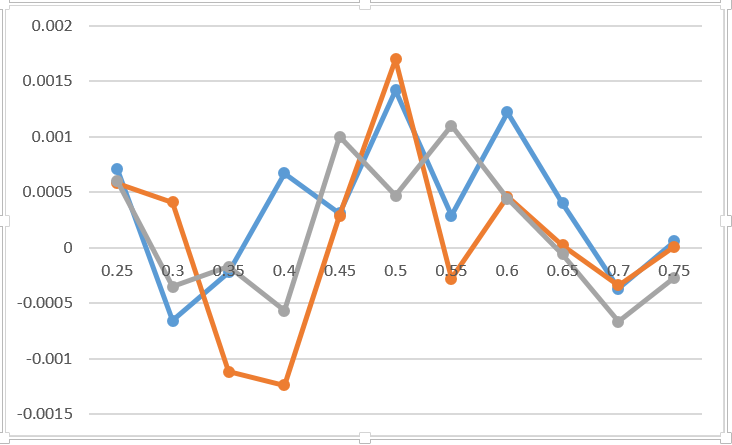
Jadi, seperti yang diperlihatkan percobaan, sama sekali tidak ada perbedaan kapan tepatnya berkonsentrasi (faktor-faktor rencana moral tidak diperhitungkan). Grafik menunjukkan perbedaan antara probabilitas memenangkan permainan dalam hal konsentrasi di 3 tempat berbeda dalam game dibandingkan dengan konsentrasi pada 3 poin pertama. Saya pikir grafik ini mencerminkan kesalahan Monte Carlo dan tidak lebih. Saya menambahkan 0,2 ke hasil undian poin untuk pemain pertama selama tiga kali imbang. Saya bahkan tidak menunjukkan pada bagan garis mana yang sesuai dengan opsi mana. Jelas tidak mengubah apa pun. Satu-satunya nasihat berharga tentang hal ini adalah bersiap-siap sebelum semuanya terlambat.
Sekarang mari kita pertimbangkan apa yang akan terjadi jika salah satu pemain memiliki stabilitas. Saraf gugup, permainan yang bertanggung jawab terjadi. Misalkan, secara rata-rata, ia memperoleh persentase poin yang sama, tetapi ketika menggambar poin tertentu, persentase ini mengapung. Sebagai contoh, setengah dari poin dimainkan dengan probabilitas p1 + delta, dan setengah lainnya dengan p1-delta. Dalam hal ini, p1 rata-rata tetap asli, hilangnya + delta atau –delta terjadi secara acak dengan probabilitas 0,5. Apakah itu akan mempengaruhi hasil permainan? Seperti percobaan saya dengan bantuan Monte Carlo menunjukkan, perbedaannya praktis tidak dilacak. Faktanya, menambah atau mengurangi jumlah tertentu, meskipun secara acak, kita tetap pada probabilitas rata-rata yang sama untuk memenangkan poin. Saran itu sendiri menunjukkan bahwa kurva distribusi tidak mempengaruhi hasil permainan, tetapi hanya rata-rata, tetapi saya tidak akan mengambilnya sendiri. Di sini Anda harus berpikir.
Saya juga ingin menurunkan persamaan diferensial, seperti Black Scholes di bidang keuangan, untuk melengkapi asosiasi. Identifikasi turunan yang signifikan, hilangkan komponen acak ... Kita juga perlu menangani diskresi. Mungkin saya akan menyerahkan ini pada matematikawan finansial sejati.