🎍 🤘🏼 🤡 Julia dan optimasi 🤨 👨🏽‍🤝‍👨🏻 🐼

Saatnya mempertimbangkan paket yang menyediakan metode untuk menyelesaikan masalah optimisasi. Banyak masalah dapat dikurangi untuk menemukan minimum beberapa fungsi, jadi Anda harus memiliki beberapa atau dua pemecah dalam arsenal, dan bahkan lebih dari satu paket keseluruhan.

Entri

Bahasa Julia terus mendapatkan popularitas . Di https://juliacomputing.com Anda dapat melihat mengapa astronom, robot, dan pemodal memilih bahasa ini, dan di https://academy.juliabox.com Anda dapat memulai kursus gratis untuk mempelajari bahasa dan menggunakannya dalam segala jenis pembelajaran mesin. Bagi mereka yang serius memutuskan untuk mulai belajar, saya menyarankan Anda untuk menonton video, membaca artikel dan mengklik laptop jupiter di https://julialang.org/learning/ atau setidaknya melalui hub dari bawah ke atas: akan ada instalasi, dan fitur, dan aplikasi untuk bisnis mendesak. Sekarang mari kita ke perpustakaan.

Blackboxoxptim

BlackBoxOptim - paket optimasi global untuk Julia ( http://julialang.org/ ). Ini mendukung masalah optimasi multi-tujuan dan tujuan tunggal dan berfokus pada (meta) heuristik / algoritma stokastik (DE, NES, dll.) Yang TIDAK memerlukan fungsi yang dioptimalkan untuk dibedakan, tidak seperti yang lebih tradisional, algoritma deterministik, yang sering didasarkan pada gradien / diferensiabilitas. Ini juga mendukung komputasi paralel untuk mempercepat optimalisasi fungsi yang dievaluasi perlahan.

Unduh dan hubungkan perpustakaan

]add BlackBoxOptim using BlackBoxOptim

Atur fungsi Rosenbrock:

 f(x) = (1.0 - x[1])^2 + 100.0 * (x[2] - x[1]^2)^2

Kami mencari minimum pada interval (-5; 5) untuk setiap koordinat untuk masalah dua dimensi:

 res = bboptimize(f; SearchRange = (-5.0, 5.0), NumDimensions = 2)

Apa jawabannya akan mengikuti:

 Starting optimization with optimizer DiffEvoOpt{FitPopulation{Float64},RadiusLimitedSelector,BlackBoxOptim.AdaptiveDiffEvoRandBin{3},RandomBound{RangePerDimSearchSpace}} 0.00 secs, 0 evals, 0 steps Optimization stopped after 10001 steps and 0.12400007247924805 seconds Termination reason: Max number of steps (10000) reached Steps per second = 80653.17866385692 Function evals per second = 81628.98454510146 Improvements/step = 0.2087 Total function evaluations = 10122 Best candidate found: [1.0, 1.0] Fitness: 0.000000000

dan banyak data yang tidak dapat dibaca, tetapi minimum ditemukan. Karena stokastik digunakan, pemanggilan fungsi akan sedikit banyak, jadi untuk tugas multidimensi lebih baik menggunakan pemilihan metode

 function rosenbrock(x) return( sum( 100*( x[2:end] - x[1:end-1].^2 ).^2 + ( x[1:end-1] - 1 ).^2 ) ) end res = compare_optimizers(rosenbrock; SearchRange = (-5.0, 5.0), NumDimensions = 30, MaxTime = 3.0);

Cembung

Cembung adalah paket Pemrograman Cembung Disiplin Julia (pemrograman cembung disiplin?). Convex.jl dapat menyelesaikan program linear, program linear integer campuran dan program cembung yang kompatibel dengan DCP menggunakan berbagai solver, termasuk Mosek, Gurobi, ECOS, SCS, dan GLPK, melalui antarmuka MathProgBase. Ini juga mendukung optimasi dengan variabel dan koefisien yang kompleks.

 using Pkg #      Pkg.add("Convex") Pkg.add("SCS")

Ada banyak contoh di situs: Tomografi (proses mengembalikan distribusi kepadatan dengan memberikan integral pada area distribusi. Misalnya, Anda dapat bekerja dengan tomografi dalam gambar hitam dan putih), memaksimalkan entropi, regresi logistik, pemrograman linier, dll.

Misalnya, Anda harus memenuhi persyaratan:

\ begin {array} {ll} \ mbox {memuaskan} & \ | x \ | _2 \ leq 100 \\ & e ^ {x_1} \ leq 5 \\ & x_2 \ geq 7 \\ & \ sqrt {x_3 x_4} \ geq x_2 \ end {array}

$\ begin {array} {ll} \ mbox {memuaskan} & \ | x \ | _2 \ leq 100 \\ & e ^ {x_1} \ leq 5 \\ & x_2 \ geq 7 \\ & \ sqrt {x_3 x_4} \ geq x_2 \ end {array}$

 using Convex, SCS, LinearAlgebra x = Variable(4) p = satisfy(norm(x) <= 100, exp(x[1]) <= 5, x[2] >= 7, geomean(x[3], x[4]) >= x[2]) solve!(p, SCSSolver(verbose=0)) println(p.status) x.value

Akan memberi jawaban

 Optimal 4×1 Array{Float64,2}: 0.0 8.554892320716046 15.329934133156783 15.329934133156783

Lompat

JuMP adalah bahasa optimisasi matematika khusus domain yang dibangun ke dalam Julia. Dia saat ini mendukung sejumlah pemecah terbuka dan komersial (Artelys Knitro, BARON, Bonmin, Cbc, Clp, Couenne, CPLEX, ECOS, FICO Xpress, GLPK, Gurobi, Ipopt, MOSEK, NLopt, SCS).

JuMP membuatnya mudah untuk mengidentifikasi dan menyelesaikan masalah optimasi tanpa pengetahuan ahli, tetapi pada saat yang sama memungkinkan para ahli untuk menerapkan metode algoritmik canggih, seperti menggunakan awal yang "panas" yang efektif dalam pemrograman linier atau menggunakan panggilan balik untuk berinteraksi dengan pemecah cabang dan batas. JuMP juga cepat - pembandingan menunjukkan bahwa ia dapat menangani perhitungan dengan kecepatan yang mirip dengan alat komersial khusus seperti AMPL, sambil mempertahankan ekspresifitas bahasa pemrograman universal tingkat tinggi. JuMP dapat dengan mudah diintegrasikan ke dalam alur kerja yang kompleks, termasuk simulasi dan server web.

Alat ini memungkinkan Anda untuk mengatasi tugas-tugas seperti:

LP = pemrograman linier
QP = Pemrograman Quadratic
SOCP = pemrograman kerucut orde kedua (termasuk masalah dengan kendala kuadratik cembung dan / atau tujuan)
MILP = Program Integer Linier Campuran
NLP = Pemrograman Nonlinear
MINLP = pemrograman nonlinier bilangan bulat campuran
SDP = pemrograman semi-didefinisikan
MISDP = pemrograman semidefinite integer campuran

Analisis kemampuannya akan cukup untuk beberapa artikel, jadi untuk sekarang mari kita beralih ke yang berikut:

Optim

Optim Ada banyak solver yang tersedia dari sumber gratis dan komersial, dan banyak yang sudah dibungkus untuk digunakan di Julia. Beberapa dari mereka ditulis dalam bahasa ini. Dalam hal kinerja, ini jarang menjadi masalah, karena mereka sering ditulis dalam Fortran atau C. Namun, pemecah masalah yang ditulis langsung dalam Julia memang memiliki beberapa kelebihan.

Saat menulis perangkat lunak Julia (paket) yang perlu dioptimalkan sesuatu, programmer dapat menulis prosedur optimasi sendiri atau menggunakan salah satu dari banyak pemecah yang tersedia. Misalnya, itu bisa berupa sesuatu dari set NLOpt. Ini berarti menambahkan ketergantungan yang tidak ditulis dalam Julia, dan Anda perlu membuat lebih banyak asumsi tentang lingkungan di mana pengguna berada. Apakah pengguna memiliki kompiler yang tepat? Bisakah saya menggunakan kode GPL dalam suatu proyek?

Juga benar bahwa menggunakan solver yang ditulis dalam C atau Fortran membuatnya tidak mungkin untuk menggunakan salah satu keunggulan utama Julia: pengiriman ganda. Karena Optim sepenuhnya ditulis dalam Julia, saat ini kami dapat menggunakan sistem pengiriman untuk membuatnya lebih mudah menggunakan preset khusus. Fitur yang direncanakan dalam arah ini adalah untuk memungkinkan pemilihan solver yang digerakkan pengguna untuk berbagai tahap algoritma, didasarkan sepenuhnya pada penjadwalan, bukan pada kemampuan yang telah ditentukan yang dipilih oleh pengembang Optim.

Paket pada Julia juga berarti bahwa Optim memiliki akses ke fungsi diferensiasi otomatis melalui paket di JuliaDiff .

Panduan

Lanjutkan:

 ]add Optim using Optim #   f(x) = (1.0 - x[1])^2 + 100.0 * (x[2] - x[1]^2)^2 x0 = [0.0, 0.0] optimize(f, x0)

Kami mendapat jawaban dengan laporan yang mudah:

 Results of Optimization Algorithm * Algorithm: Nelder-Mead #   * Starting Point: [0.0,0.0] * Minimizer: [0.9999634355313174,0.9999315506115275] * Minimum: 3.525527e-09 * Iterations: 60 * Convergence: true * √(Σ(yᵢ-ȳ)²)/n < 1.0e-08: true * Reached Maximum Number of Iterations: false * Objective Calls: 118

Dan bandingkan dengan Nelder Mead saya!

spoiler

Milik saya akan lebih lambat :(

Terselip

 using BenchmarkTools @benchmark optimize(f, x0) BenchmarkTools.Trial: memory estimate: 11.00 KiB allocs estimate: 419 -------------- minimum time: 39.078 μs (0.00% GC) median time: 43.420 μs (0.00% GC) mean time: 53.024 μs (15.02% GC) maximum time: 59.992 ms (99.83% GC) -------------- samples: 10000 evals/sample: 1

Selama pemeriksaan, ternyata implementasi saya tidak berfungsi jika Anda menggunakan perkiraan awal (0, 0). Sebagai kriteria penghentian, Anda dapat menggunakan volume simpleks , tetapi saya menggunakan norma matriks yang terdiri dari simpul. Di sini Anda dapat membaca tentang interpretasi geometrik norma. Dalam kedua kasus, matriks nol diperoleh - kasus khusus dari matriks degenerasi, oleh karena itu, metode ini tidak melakukan langkah apa pun. Anda dapat mengkonfigurasi pembuatan simpleks awal, misalnya, dengan mengatur jarak simpulnya dari perkiraan awal (dan tidak seperti milik saya - setengah dari panjang vektor, fu, sayang sekali ...), maka pengaturan metode akan lebih fleksibel, atau pastikan bahwa semua simpul tidak duduk di satu titik:

  for i = 1:N+1 Xx[:,i] = fit end for i = 1:N Xx[i,i] += 0.5*vecl(fit) + ε end

Yah ya, goraaazdo simpleks saya lebih lambat:

 ofNelderMid(fit = [0, 0.]) step= 118 7.7234e-5 f = 2.797-18 x = [1.0, 1.0] @benchmark ofNelderMid(fit = [0., 0.]) BenchmarkTools.Trial: memory estimate: 394.03 KiB allocs estimate: 6632 -------------- minimum time: 717.221 μs (0.00% GC) median time: 769.325 μs (0.00% GC) mean time: 854.644 μs (5.04% GC) maximum time: 50.429 ms (98.01% GC) -------------- samples: 5826 evals/sample: 1

Sekarang lebih banyak alasan untuk kembali ke paket studi

Anda dapat memilih metode yang digunakan:

 optimize(f, x0, LBFGS()) Results of Optimization Algorithm * Algorithm: L-BFGS * Starting Point: [0.0,0.0] * Minimizer: [0.9999999926662504,0.9999999853325008] * Minimum: 5.378388e-17 * Iterations: 24 * Convergence: true * |x - x'| ≤ 0.0e+00: false |x - x'| = 4.54e-11 * |f(x) - f(x')| ≤ 0.0e+00 |f(x)|: false |f(x) - f(x')| = 5.30e-03 |f(x)| * |g(x)| ≤ 1.0e-08: true |g(x)| = 9.88e-14 * Stopped by an increasing objective: false * Reached Maximum Number of Iterations: false * Objective Calls: 67 * Gradient Calls: 67

dan dapatkan dokumentasi dan referensi terperinci untuk itu

 ?LBFGS()

Anda dapat mengatur fungsi Jacobian dan Hessian

 function g!(G, x) G[1] = -2.0 * (1.0 - x[1]) - 400.0 * (x[2] - x[1]^2) * x[1] G[2] = 200.0 * (x[2] - x[1]^2) end function h!(H, x) H[1, 1] = 2.0 - 400.0 * x[2] + 1200.0 * x[1]^2 H[1, 2] = -400.0 * x[1] H[2, 1] = -400.0 * x[1] H[2, 2] = 200.0 end optimize(f, g!, h!, x0) Results of Optimization Algorithm * Algorithm: Newtons Method * Starting Point: [0.0,0.0] * Minimizer: [0.9999999999999994,0.9999999999999989] * Minimum: 3.081488e-31 * Iterations: 14 * Convergence: true * |x - x'| ≤ 0.0e+00: false |x - x'| = 3.06e-09 * |f(x) - f(x')| ≤ 0.0e+00 |f(x)|: false |f(x) - f(x')| = 3.03e+13 |f(x)| * |g(x)| ≤ 1.0e-08: true |g(x)| = 1.11e-15 * Stopped by an increasing objective: false * Reached Maximum Number of Iterations: false * Objective Calls: 44 * Gradient Calls: 44 * Hessian Calls: 14

Seperti yang Anda lihat, dia secara otomatis mengerjakan metode Newton. Dan Anda dapat mengatur area pencarian dan menggunakan gradient descent:

 lower = [1.25, -2.1] upper = [Inf, Inf] initial_x = [2.0, 2.0] inner_optimizer = GradientDescent() results = optimize(f, g!, lower, upper, initial_x, Fminbox(inner_optimizer)) Results of Optimization Algorithm * Algorithm: Fminbox with Gradient Descent * Starting Point: [2.0,2.0] * Minimizer: [1.2500000000000002,1.5625000000000004] * Minimum: 6.250000e-02 * Iterations: 8 * Convergence: true * |x - x'| ≤ 0.0e+00: true |x - x'| = 0.00e+00 * |f(x) - f(x')| ≤ 0.0e+00 |f(x)|: true |f(x) - f(x')| = 0.00e+00 |f(x)| * |g(x)| ≤ 1.0e-08: false |g(x)| = 5.00e-01 * Stopped by an increasing objective: false * Reached Maximum Number of Iterations: false * Objective Calls: 84382 * Gradient Calls: 84382

Ya, atau saya tidak tahu, katakanlah Anda ingin menyelesaikan persamaan

 f_univariate(x) = 2x^2+3x+1 optimize(f_univariate, -2.0, 1.0) Results of Optimization Algorithm * Algorithm: Brents Method * Search Interval: [-2.000000, 1.000000] * Minimizer: -7.500000e-01 * Minimum: -1.250000e-01 * Iterations: 7 * Convergence: max(|x - x_upper|, |x - x_lower|) <= 2*(1.5e-08*|x|+2.2e-16): true * Objective Function Calls: 8

dan dia memilihmu Metode Brent .
Atau memiliki data eksperimental, Anda perlu mengoptimalkan koefisien model

F (p_{1}, p_{2}, x) = p_{1} c o s (p_{2} x) + p_{2} s i n (p_{1} x)

$F (p_1, p_2, x) = p_1 \ cos (p_2x) + p_2 \ sin (p_1x)$

p_{1} = 1, p_{2} = 0, 2

$p_1 = 1, p_2 = 0,2$

 F(p, x) = p[1]*cos(p[2]*x) + p[2]*sin(p[1]*x) model(p) = sum( [ (F(p, xdata[i]) - ydata[i])^2 for i = 1:length(xdata)] ) xdata = [-2,-1.64,-1.33,-0.7,0,0.45,1.2,1.64,2.32,2.9] ydata = [0.699369,0.700462,0.695354,1.03905,1.97389,2.41143,1.91091,0.919576,-0.730975,-1.42001] res2 = optimize(model, [1.0, 0.2]) Results of Optimization Algorithm * Algorithm: Nelder-Mead * Starting Point: [1.0,0.2] * Minimizer: [1.8818299027162517,0.7002244825046421] * Minimum: 5.381270e-02 * Iterations: 34 * Convergence: true * √(Σ(yᵢ-ȳ)²)/n < 1.0e-08: true * Reached Maximum Number of Iterations: false * Objective Calls: 71

 P = Optim.minimizer(res2) Y = [ F(P, x) for x in xdata] using Plots plotly() plot(xdata, ydata) plot!(xdata, Y)

Bonus Buat fungsi pengujian Anda

Idenya digunakan dari artikel Khabrov . Anda dapat mengonfigurasi setiap minimum lokal sendiri:

 """ https://habr.com/ru/post/349660/ :param n:   :param a:    ,   ,    /      :param c:    :param p:       :param b:    :return:  ,       ,          """ function feldbaum(x; n=5, a=[3 2; 4 3; 2 1; 4 5; .5 .5], c=[-1 2; 2 1; -3 2; -2 -2; 1.5 -2], p=[9 6; 1 1; 1.5 1.4; 1.2 1.3; 0.5 0.5], b=[0 1 3.2 2 4.6]) l = zeros(n) for i = 1:n res = 0 for j = 1:size(x,1) res += a[i,j] * abs(x[j] - c[i,j]) ^ p[i,j] end res += b[i] l[i] = res end minimum(l) end

Dan Anda dapat meninggalkan segalanya sesuai kehendak acak yang maha kuasa

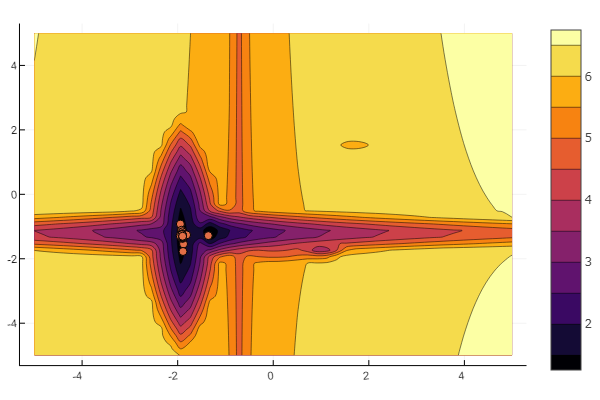
 n=10 m = 2 a = rand(0:0.1:6, n, m) c = rand(-2:0.1:2, n, m) p = rand(0:0.1:2, n, m) b = rand(0:0.1:8, n, m) function feldbaum(x) l = zeros(n) for i = 1:n res = 0 for j = 1:m res += a[i,j] * abs(x[j] - c[i,j]) ^ p[i,j] end res += b[i] l[i] = res end minimum(l) end

Tapi seperti yang bisa Anda lihat dari gambar awal, segerombolan partikel dengan bantuan seperti itu tidak mengintimidasi.

Ini harus dilakukan. Seperti yang Anda lihat, Julia memiliki lingkungan matematika yang cukup kuat dan modern yang memungkinkan studi numerik yang rumit untuk dilakukan tanpa turun ke abstraksi pemrograman tingkat rendah. Dan ini adalah kesempatan yang bagus untuk terus belajar bahasa ini.

Semoga beruntung untuk semuanya!