✋🏿 🎏 🔝 Pemrograman relasional: rasa sakit, minat, dan rasa sakit lagi 📍 👩🏿‍🤝‍👩🏽 👈🏽

Dalam posting sebelumnya kami memberi tahu secara rinci apa yang kami ajarkan kepada siswa di bidang "Pemrograman Industri". Bagi mereka yang bidang minatnya terletak pada bidang yang lebih teoretis, misalnya, tertarik oleh paradigma pemrograman baru atau matematika abstrak yang digunakan dalam penelitian teoritis tentang pemrograman, ada spesialisasi lain - “Bahasa pemrograman”.

Hari ini saya akan berbicara tentang penelitian saya di bidang pemrograman relasional, yang saya lakukan di universitas dan sebagai mahasiswa-peneliti di laboratorium alat bahasa JetBrains Research.

Apa itu pemrograman relasional? Biasanya kita menjalankan fungsi dengan argumen dan mendapatkan hasilnya. Dan dalam kasus relasional, Anda dapat melakukan yang sebaliknya: perbaiki hasil dan satu argumen, dan dapatkan argumen kedua. Yang utama adalah menulis kode dengan benar dan bersabar dan memiliki cluster yang baik.

Tentang diri saya

Nama saya Dmitry Rozplokhas, saya adalah mahasiswa tahun pertama HSE St. Petersburg, dan tahun lalu saya lulus dari program sarjana di Universitas Akademik di bidang “Bahasa Pemrograman”. Sejak tahun ketiga studi sarjana, saya juga seorang mahasiswa peneliti di laboratorium alat bahasa Penelitian JetBrains.

Pemrograman relasional

Fakta umum

Pemrograman relasional adalah ketika, alih-alih fungsi, Anda menggambarkan hubungan antara argumen dan hasilnya. Jika bahasa diasah untuk ini, Anda bisa mendapatkan bonus tertentu, misalnya, kemampuan untuk menjalankan fungsi dalam arah yang berlawanan (mengembalikan nilai yang mungkin dari argumen sebagai hasilnya).

Secara umum, ini dapat dilakukan dalam bahasa logis apa pun, tetapi minat dalam pemrograman relasional muncul bersamaan dengan munculnya miniKanren bahasa logis murni minimalis sekitar sepuluh tahun yang lalu, yang memungkinkan untuk dengan mudah menggambarkan dan menggunakan hubungan seperti itu.

Berikut adalah beberapa kasus penggunaan paling canggih: Anda dapat menulis pemeriksa bukti dan menggunakannya untuk menemukan bukti ( Near et al., 2008 ), atau membuat penerjemah untuk beberapa bahasa dan menggunakannya untuk menghasilkan program suite uji ( Byrd et al., 2017 ).

Sintaks dan Contoh Mainan

miniKanren adalah bahasa kecil, hanya konstruksi matematika dasar yang digunakan untuk menggambarkan hubungan. Ini adalah bahasa yang disematkan, primitifnya adalah perpustakaan untuk beberapa bahasa eksternal, dan program miniKanren kecil dapat digunakan di dalam suatu program dalam bahasa lain.

Bahasa asing cocok untuk miniKanren, sejumlah besar. Awalnya, ada Skema, kami bekerja dengan versi untuk Ocaml ( OCanren ), dan daftar lengkapnya dapat dilihat di minikanren.org . Contoh dalam artikel ini juga ada di OCanren. Banyak implementasi menambahkan fungsi pembantu, tetapi kami hanya akan fokus pada bahasa inti.

Mari kita mulai dengan tipe data. Secara konvensional, mereka dapat dibagi menjadi dua jenis:

Konstanta adalah beberapa data dari bahasa yang menjadi asal kita. String, angka, bahkan array. Tetapi untuk miniKanren dasar, ini semua kotak hitam, konstanta hanya dapat diperiksa untuk kesetaraan.
"Istilah" adalah tupel dari beberapa elemen. Umumnya digunakan dengan cara yang sama seperti konstruktor data di Haskell: konstruktor data (string) ditambah nol atau lebih parameter. OCanren menggunakan konstruktor data reguler dari OCaml.

Misalnya, jika kita ingin bekerja dengan array di miniKanren itu sendiri, maka harus dijelaskan dalam istilah yang mirip dengan bahasa fungsional - sebagai daftar yang terhubung secara tunggal. Daftar adalah daftar kosong (ditunjukkan oleh beberapa istilah sederhana), atau sepasang elemen pertama dari daftar ("head") dan elemen lainnya ("tail").

let emptyList = Nil let list_123 = Cons (1, Cons (2, Cons (3, Nil)))

Program miniKanren adalah hubungan antara beberapa variabel. Saat startup, program memberikan semua nilai yang mungkin dari variabel dalam bentuk umum. Seringkali implementasi memungkinkan Anda membatasi jumlah jawaban dalam output, misalnya, hanya temukan yang pertama - pencarian tidak selalu berhenti setelah menemukan semua solusi.

Anda dapat menulis beberapa hubungan yang didefinisikan melalui satu sama lain dan bahkan disebut secara rekursif sebagai fungsi. Misalnya, di bawah ini kita bukan fungsi

a p p e n d (a, b) \to d e n g a n

$append (a, b) → dengan$ tentukan hubungannya

a p p e n d o (a, b, c)

$appendo (a, b, c)$ : daftar

c

$c$ adalah gabungan daftar

a

$a$ dan

b

$b$ . Fungsi yang mengembalikan hubungan secara tradisional diakhiri dengan "o" untuk membedakannya dari fungsi biasa.

Suatu relasi ditulis sebagai beberapa pernyataan mengenai argumennya. Kami memiliki empat operasi dasar :

Penyatuan atau persamaan (===) dari dua istilah, istilah dapat mencakup variabel. Misalnya, Anda dapat menulis daftar relasi terdiri dari satu elemen ":
```
 let isSingletono xl = l === Cons (x, Nil) 
```
Konjungsi (logis "dan") dan disjungsi (logis "atau") - seperti dalam logika biasa. OCanren disebut sebagai &&& dan |||. Tetapi pada dasarnya tidak ada penolakan logis dalam MiniKanren.
Menambahkan variabel baru. Dalam logika, ini adalah penjumlahan keberadaan. Misalnya, untuk memeriksa daftar untuk ketidak-kosongan, Anda perlu memeriksa bahwa daftar itu terdiri atas kepala dan ekor. Mereka bukan argumen hubungan, jadi Anda perlu membuat variabel baru:
```
 let nonEmptyo l = fresh (ht) (l === Cons (h, t)) 
```

Suatu hubungan dapat memunculkan dirinya secara rekursif. Misalnya, Anda perlu mendefinisikan elemen "hubungan

x

$x$ terletak pada daftar. " Kami akan memecahkan masalah ini dengan menganalisis kasus-kasus sepele, seperti dalam bahasa fungsional:

Atau kepala daftar adalah $x$
Baik $x$ terletak di ekor

 let membero lx = fresh (ht) ( (l === Cons (h, t)) &&& (x === h ||| membero tx) )

Versi dasar bahasa dibangun pada empat operasi ini. Ada juga ekstensi yang memungkinkan Anda menggunakan operasi lain. Yang paling berguna dari mereka adalah kendala ketidaksetaraan untuk mengatur ketidaksetaraan dua istilah (= / =).

Meskipun minimalis, miniKanren adalah bahasa yang cukup ekspresif. Sebagai contoh, lihatlah gabungan dari dua daftar relasional. Fungsi dua argumen berubah menjadi hubungan rangkap tiga "

a b

$ab$ adalah gabungan daftar

a

$a$ dan

b

$b$ ".

 let appendo ab ab = (a === Nil &&& ab === b) ||| (fresh (ht tb) (*  :  fresh   &&& *) (a = Cons (h, t)) (appendo tb tb) (ab === Cons (h, tb)))

Solusinya secara struktural tidak berbeda dari bagaimana kita akan menulisnya dalam bahasa fungsional. Kami menganalisis dua kasus yang disatukan oleh klausa:

Jika daftar pertama kosong, maka daftar kedua dan hasil gabungan adalah sama.
Jika daftar pertama tidak kosong, maka kami menguraikannya ke kepala dan ekor dan membangun hasilnya menggunakan panggilan relasional rekursif.

Kami dapat membuat permintaan untuk relasi ini, memperbaiki argumen pertama dan kedua - kami mendapatkan rangkaian daftar:

 run 1 (λ q -> appendo (Cons (1, Cons (2, Nil))) (Cons (3, Cons (4, Nil))) q)

⇒

 q = Cons (1, Cons (2, Cons (3, Cons (4, Nil))))

Kami dapat memperbaiki argumen terakhir - kami membuat semua partisi daftar ini menjadi dua.

 run 4 (λ qr -> appendo qr (Cons (1, Cons (2, Cons (3, Nil)))))

⇒

 q = Nil, r = Cons (1, Cons (2, Cons (3, Nil))) | q = Cons (1, Nil), r = Cons (2, Cons (3, Nil)) | q = Cons (1, Cons (2, Nil)), r = Cons (3, Nil) | q = Cons (1, Cons (2, Cons (3, Nil))), r = Nil

Anda dapat melakukan hal lain. Contoh yang sedikit lebih tidak standar, di mana kami hanya memperbaiki sebagian dari argumen:

 run 1 (λ qr -> appendo (Cons (1, Cons (q, Nil))) r (Cons (1, Cons (2, Cons (3, Cons (4, Nil))))))

⇒

 q = 2, r = Cons (3, Cons (4, Nil))

Bagaimana cara kerjanya

Dari sudut pandang teori, tidak ada yang mengesankan di sini: Anda selalu dapat mulai mencari semua opsi yang mungkin untuk semua argumen, memeriksa setiap set apakah mereka berperilaku sehubungan dengan fungsi / hubungan yang diberikan seperti yang kita inginkan (lihat "Algoritma Museum Inggris" ) . Yang menarik adalah fakta bahwa di sini pencarian (dengan kata lain, pencarian solusi) hanya menggunakan struktur hubungan yang dijelaskan, karena itu dapat relatif efektif dalam praktik.

Pencarian terkait dengan mengumpulkan informasi tentang berbagai variabel dalam kondisi saat ini. Kami tidak tahu apa-apa tentang setiap variabel, atau kami tahu bagaimana itu dinyatakan dalam istilah, nilai, dan variabel lainnya. Sebagai contoh:

b = Cons (x, y)
c = Cons (10, z)
x = ?
y = ?
z = ?

Melewati penyatuan, kami melihat dua istilah dengan informasi ini dalam pikiran dan memperbarui keadaan atau menghentikan pencarian jika dua istilah tidak dapat disatukan. Misalnya, menyelesaikan penyatuan b = c, kami mendapatkan informasi baru: x = 10, y = z. Tetapi penyatuan b = Nihil akan menyebabkan kontradiksi.

Kami mencari dalam konjungsi secara berurutan (sehingga informasi terakumulasi), dan dalam disjungsi kami membagi pencarian menjadi dua cabang paralel dan melanjutkan, bergantian langkah di dalamnya - inilah yang disebut pencarian interleaving. Berkat pergantian ini, pencarian selesai - setiap solusi yang cocok akan ditemukan setelah waktu yang terbatas. Misalnya, dalam bahasa Prolog ini tidak demikian. Ia melakukan sesuatu seperti perayapan yang dalam (yang dapat bertahan di cabang yang tak terbatas), dan pencarian yang saling terkait pada dasarnya adalah modifikasi perayapan yang rumit dan rumit.

Sekarang mari kita lihat bagaimana kueri pertama dari bagian sebelumnya bekerja. Karena appendo memiliki panggilan rekursif, kami akan menambahkan indeks ke variabel untuk membedakannya. Gambar di bawah ini menunjukkan pohon enumerasi. Panah menunjukkan arah penyebaran informasi (kecuali untuk pengembalian dari rekursi). Di antara disjungsi, informasi tidak didistribusikan, dan di antara konjungsi didistribusikan dari kiri ke kanan.

Kami mulai dengan panggilan eksternal untuk menambah. Cabang disjungsi kiri mati karena kontroversi: daftar $a$ tidak kosong.
Di cabang kanan variabel tambahan diperkenalkan, yang kemudian digunakan untuk "mem-parsing" daftar $a_1$ di kepala dan ekor.
Setelah ini, appendo recursive call terjadi untuk a = [2], b = [3, 4], ab = ?, di mana operasi serupa terjadi.
Tetapi dalam panggilan ketiga untuk appendo kita sudah memiliki a = [], b = [3,4], ab =?, Dan kemudian disjungsi kiri hanya berfungsi, setelah itu kita mendapatkan informasi ab = b. Tetapi di cabang kanan ada kontradiksi.
Sekarang kita dapat menuliskan semua informasi yang tersedia dan mengembalikan jawabannya dengan mengganti nilai-nilai variabel:

a_1 = [1, 2] b_1 = [3, 4] ab_1 = Cons h_1 tb_1 h_1 = 1 a_2 = t_1 = [2] b_2 = b_1 = [3, 4] ab_2 = tb_1 = Cons h_2 tb_2 h_2 = 2 a_3 = t_2 = Nil b_3 = b_2 = b_1 = [3, 4] ab_3 = tb_2 = b_3 = [3, 4]
Karena itu $ab_1$ = Kontra (1, Kontra (2, [3, 4]))) = [1, 2, 3, 4], sesuai kebutuhan.

Apa yang saya lakukan di sarjana

Semuanya melambat

Seperti biasa: mereka berjanji kepada Anda bahwa semuanya akan menjadi super deklaratif, tetapi dalam kenyataannya Anda perlu beradaptasi dengan bahasa dan menulis semuanya dengan cara khusus (dengan mengingat bagaimana semuanya akan dieksekusi) agar setidaknya ada sesuatu yang berfungsi, kecuali untuk contoh sederhana. Ini mengecewakan.

Salah satu masalah pertama yang dihadapi oleh seorang programmer miniKanren pemula adalah bahwa hal itu sangat tergantung pada urutan di mana Anda menggambarkan kondisi (konjungsi) dalam program. Dengan satu urutan, semuanya baik-baik saja, tetapi dua konjungsi ditukar dan semuanya mulai bekerja sangat lambat atau tidak selesai sama sekali. Ini tidak terduga.

Bahkan dalam contoh dengan appendo, meluncurkan ke arah yang berlawanan (menghasilkan pemisahan daftar menjadi dua) tidak berakhir kecuali Anda secara eksplisit menentukan berapa banyak jawaban yang Anda inginkan (maka pencarian akan berakhir setelah nomor yang diperlukan ditemukan).

Misalkan kita memperbaiki variabel asli sebagai berikut: a =?, B =?, Ab = [1, 2, 3] (lihat gambar di bawah) Di cabang kedua, informasi ini tidak akan digunakan dengan cara apa pun selama panggilan rekursif (variabel ab dan batasan pada

h_{1}

$h_1$ dan

t b_{1}

$tb_1$ hanya muncul setelah panggilan ini). Oleh karena itu, pada panggilan rekursif pertama, semua argumennya akan menjadi variabel bebas. Panggilan ini akan menghasilkan semua jenis tiga kali lipat dari dua daftar dan rangkaiannya (dan generasi ini tidak akan pernah berakhir), dan kemudian di antara mereka akan dipilih yang mana elemen ketiga adalah persis yang kita butuhkan.

Semuanya tidak seburuk kelihatannya pada pandangan pertama, karena kita akan memilah tiga kali lipat dalam kelompok besar. Daftar dengan panjang yang sama tetapi elemen yang berbeda tidak berbeda dari sudut pandang fungsi, oleh karena itu mereka akan jatuh ke dalam satu solusi - akan ada variabel bebas di tempat elemen. Namun demikian, kami masih akan memilah-milah semua daftar panjang yang mungkin, meskipun kami hanya membutuhkan satu, dan kami tahu yang mana. Ini adalah penggunaan informasi yang sangat tidak rasional (tidak digunakan) dalam pencarian.

Contoh khusus ini mudah diperbaiki: Anda hanya perlu memindahkan panggilan rekursif ke akhir dan semuanya akan berfungsi sebagaimana mestinya. Sebelum panggilan rekursif, penyatuan dengan variabel ab akan terjadi dan panggilan rekursif akan dilakukan dari ekor daftar yang diberikan (sebagai fungsi rekursif normal). Definisi ini dengan panggilan rekursif pada akhirnya akan bekerja dengan baik di semua arah: untuk panggilan rekursif, kami berhasil mengumpulkan semua informasi yang mungkin tentang argumen.

Namun, dalam contoh yang sedikit lebih kompleks, ketika ada beberapa panggilan yang bermakna, satu urutan khusus yang semuanya akan baik-baik saja tidak ada. Contoh paling sederhana: memperluas daftar menggunakan gabungan. Kami memperbaiki argumen pertama - kami membutuhkan pesanan khusus ini, kami memperbaiki yang kedua - kami perlu menukar panggilan. Kalau tidak, itu dicari untuk waktu yang lama dan pencarian tidak berakhir.

 reverso x xr = (x === Nil &&& xr == Nil) ||| (fresh (ht tr) (x === Cons (h, t)) (reverso t tr) (appendo tr (Cons (h, Nil)) xr))

Ini karena interleaving proses pencarian berhubungan secara berurutan, dan tidak ada yang bisa memikirkan bagaimana melakukannya secara berbeda tanpa kehilangan efisiensi yang dapat diterima, meskipun mereka mencoba. Tentu saja, semua solusi suatu hari nanti akan ditemukan, tetapi dengan urutan yang salah, mereka akan dicari begitu lama sehingga tidak ada arti praktis dalam hal ini.

Ada teknik untuk menulis program untuk menghindari masalah ini. Tetapi banyak dari mereka membutuhkan keterampilan dan imajinasi khusus untuk digunakan, dan hasilnya adalah program yang sangat besar. Contohnya adalah teknik batasan ukuran istilah dan definisi pembagian biner dengan sisa melalui perkalian dengan bantuannya. Alih-alih bodoh menulis definisi matematika

 divo nmqr = (fresh (mq) (multo mq mq) (pluso mq rn) (lto rm))

Saya harus menulis definisi rekursif 20 baris + fungsi bantu besar yang tidak realistis untuk dibaca (saya masih tidak mengerti apa yang sedang dilakukan di sana). Ini dapat ditemukan dalam disertasi Will Bird di bagian Aritmatika Biner Murni.

Mengingat hal tersebut di atas, saya ingin membuat semacam modifikasi pencarian sehingga program yang ditulis dengan sederhana dan alami juga berfungsi.

Optimalkan

Kami perhatikan bahwa ketika semuanya buruk, pencarian tidak akan berakhir kecuali Anda secara eksplisit menunjukkan jumlah jawaban dan memecahkannya. Oleh karena itu, mereka memutuskan untuk bertarung tepat dengan ketidaklengkapan pencarian - jauh lebih mudah untuk dikonkritkan daripada “itu bekerja untuk waktu yang lama”. Secara umum, tentu saja, saya hanya ingin mempercepat pencarian, tetapi jauh lebih sulit untuk diformalkan, jadi kami mulai dengan tugas yang kurang ambisius.

Dalam kebanyakan kasus, ketika pencarian berbeda, terjadi situasi yang mudah dilacak. Jika suatu fungsi disebut rekursif, dan dalam panggilan rekursif, argumennya sama atau kurang spesifik, maka dalam panggilan rekursif yang lain subtugas tersebut dihasilkan lagi dan rekursi tak terbatas terjadi. Secara formal, kedengarannya seperti ini: ada substitusi, yang berlaku untuk argumen baru, kita mendapatkan yang lama. Misalnya, pada gambar di bawah ini, panggilan rekursif adalah generalisasi dari aslinya: Anda dapat menggantinya

c_{2}

$c_2$ = [x, 3],

d_{2}

$d_2$ = x dan dapatkan panggilan asli.

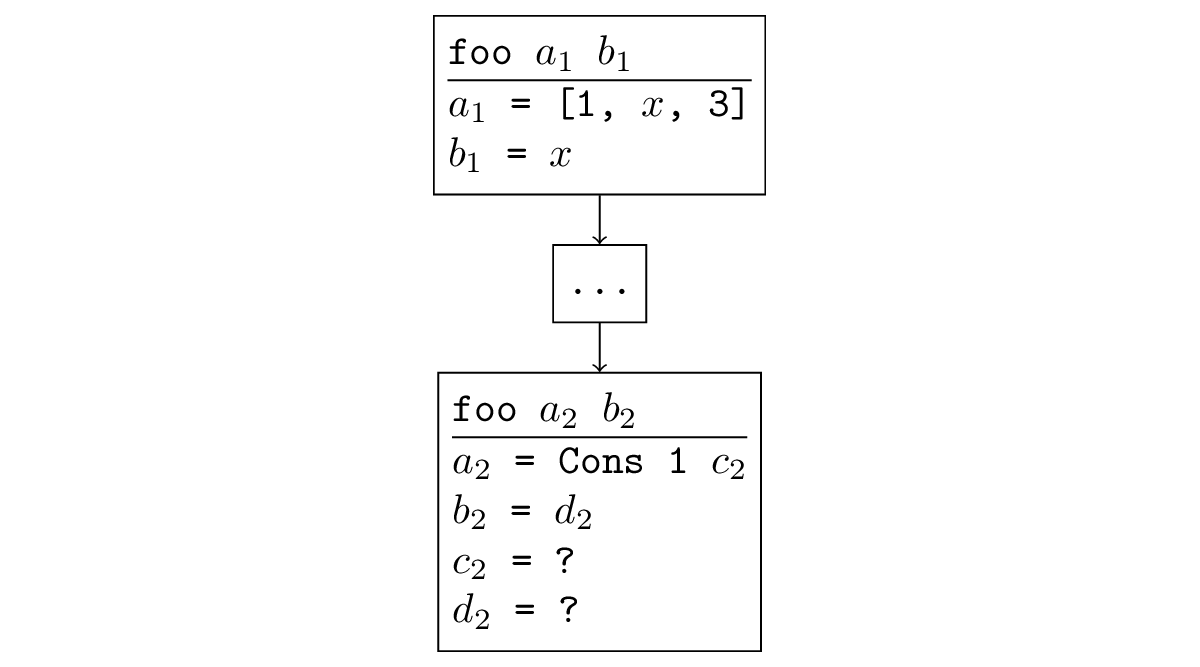
Dapat ditelusuri bahwa situasi ini juga terjadi dalam contoh divergensi yang telah kita temui. Seperti yang saya tulis sebelumnya, ketika Anda menjalankan appendo ke arah yang berlawanan, panggilan rekursif akan dibuat dengan variabel bebas, bukan semua variabel, yang, tentu saja, kurang spesifik daripada panggilan asli, di mana argumen ketiga diperbaiki.

Jika kita menjalankan reverso dengan x =? dan xr = [1, 2, 3], dapat dilihat bahwa panggilan rekursif pertama akan kembali terjadi dengan dua variabel bebas, sehingga argumen baru jelas dapat ditransfer kembali ke yang sebelumnya.

 reverso x x_r  (* x = ?, x_r = [1, 2, 3] *) fresh (ht t_r) (x === Cons (h, t)) (* x_r = [1, 2, 3] = Cons 1 (Cons 2 (Cons 3 Nil))) x = Cons (h, t) *) (reverso t t_r) (* :   t=x, t_r=[1,2,3],    *)

Dengan menggunakan kriteria ini, kita dapat mendeteksi divergensi dalam proses eksekusi program, memahami bahwa semuanya buruk dengan urutan ini, dan secara dinamis mengubahnya ke yang lain. Berkat ini, idealnya, urutan yang tepat akan dipilih untuk setiap panggilan.
Anda dapat melakukannya dengan naif: jika perbedaan ditemukan dalam kata sambung, maka kami memalu semua jawaban yang telah ia temukan dan menunda pelaksanaannya sampai nanti, "melewatkan" konjungsi berikutnya. Kemudian, mungkin, ketika kita terus menjalankannya, lebih banyak informasi akan diketahui dan perbedaan tidak akan muncul. Dalam contoh kami, ini akan mengarah pada konjungsi swap yang diinginkan.

Ada cara yang kurang naif yang memungkinkan, misalnya, untuk tidak kehilangan pekerjaan yang sudah dilakukan, menunda kinerja. Sudah dengan varian paling bodoh dari mengubah urutan, divergensi telah menghilang dalam semua contoh sederhana yang menderita non-komutatif dari konjungsi, yang kita tahu, termasuk:

menyortir daftar angka (ini juga merupakan generasi dari semua permutasi daftar),
Aritmetika peano dan aritmetika biner,
generasi pohon biner dengan ukuran tertentu.

Ini merupakan kejutan yang tidak terduga bagi kami. Selain perbedaan, pengoptimalan juga berjuang melawan perlambatan program. Diagram di bawah ini menunjukkan waktu eksekusi program dengan dua perintah yang berbeda dalam hubungannya (relatif berbicara, salah satu yang terbaik dan satu dari banyak yang buruk). Diluncurkan pada komputer dengan konfigurasi Intel Core i7 CPU M 620, 2,67GHz x 4, 8GB RAM dengan sistem operasi Ubuntu 16.04.

Ketika pesanan sudah optimal (kami memilihnya dengan tangan), optimasi sedikit memperlambat eksekusi, tetapi tidak kritis

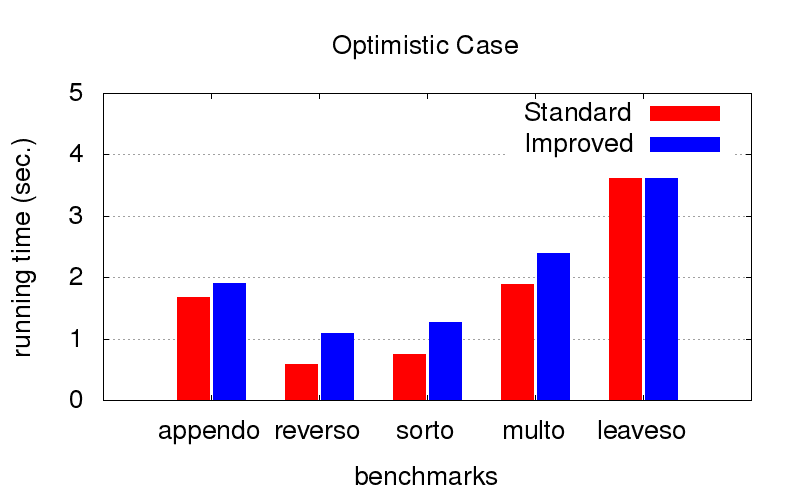
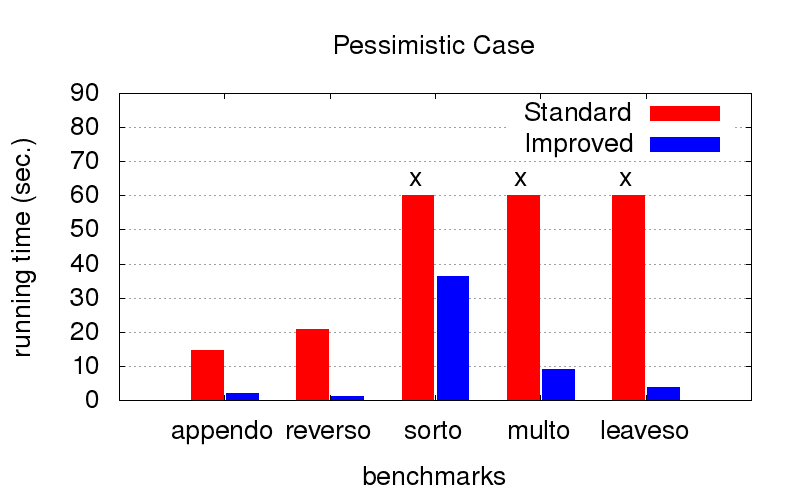
Tetapi ketika urutannya tidak optimal (misalnya, hanya cocok untuk diluncurkan pada arah yang berlawanan), dengan pengoptimalan ternyata jauh lebih cepat. Persilangan berarti bahwa kita tidak bisa menunggu sampai akhir, itu bekerja lebih lama

Cara memecahkan apa pun

Semua ini didasarkan pada intuisi dan kami ingin membuktikannya dengan ketat. Teori setelah semua.

Untuk membuktikan sesuatu, kita perlu semantik formal bahasa. Kami menggambarkan semantik operasional untuk miniKanren. Ini adalah versi yang disederhanakan dan secara matematis dari implementasi bahasa nyata. Ini menggunakan versi yang sangat terbatas (karena itu mudah digunakan), di mana Anda hanya dapat menentukan eksekusi akhir program (pencarian harus final). Tetapi untuk tujuan kita, inilah yang dibutuhkan.

Untuk membuktikan kriteria, lemma pertama kali dirumuskan: pelaksanaan program dari keadaan yang lebih umum akan bekerja lebih lama. Secara formal: pohon output dalam semantik memiliki ketinggian besar. Ini dibuktikan dengan induksi, tetapi pernyataan itu harus digeneralisasikan dengan sangat hati-hati, jika tidak, hipotesis induktif tidak akan cukup kuat. Ini mengikuti dari lemma ini bahwa jika kriteria bekerja selama eksekusi program, maka pohon output memiliki subtree sendiri lebih tinggi atau sama tinggi. Ini memberikan kontradiksi, karena untuk semantik yang diberikan secara induktif semua pohon terbatas. Ini berarti bahwa dalam semantik kami, eksekusi program ini tidak dapat diekspresikan, yang menyiratkan bahwa pencarian di dalamnya tidak berakhir.

Metode yang diusulkan adalah konservatif: kita mengubah sesuatu hanya ketika kita yakin bahwa semuanya sudah benar-benar buruk dan tidak mungkin menjadi lebih buruk, oleh karena itu kita tidak merusak apa pun dalam hal penyelesaian program.

Bukti utama berisi banyak detail, jadi kami memiliki keinginan untuk memverifikasinya secara formal dengan menulis ke Coq . Namun, ternyata secara teknis cukup sulit, jadi kami mendinginkan semangat kami dan secara serius terlibat dalam verifikasi otomatis hanya di lembaga magistrasi.

Posting

Di tengah pekerjaan, kami mempresentasikan studi ini di sesi poster ICFP-2017 di Kompetisi Penelitian Mahasiswa . Di sana kami bertemu dengan pencipta bahasa - Will Bird dan Daniel Friedman - dan mereka mengatakan bahwa itu bermakna dan kita perlu melihatnya secara lebih rinci. Ngomong-ngomong, Will umumnya berteman dengan laboratorium kami di JetBrains Research. Semua penelitian kami tentang miniKanren dimulai ketika, pada 2015, Will mengadakan sekolah musim panas dalam pemrograman relasional di St. Petersburg.

Setahun kemudian, kami membawa karya kami ke bentuk yang kurang lebih lengkap dan mempresentasikan artikel di Prinsip dan Praktek Pemrograman Deklaratif 2018.

Apa yang saya lakukan di sekolah pascasarjana

Kami ingin terus terlibat dalam semantik formal untuk mini Kanren dan bukti kuat semua propertinya. Dalam literatur, biasanya properti (seringkali jauh dari jelas) hanya dipostulatkan dan didemonstrasikan menggunakan contoh, tetapi tidak ada yang membuktikan apa pun. Misalnya, buku utama tentang pemrograman relasional adalah daftar pertanyaan dan jawaban, yang masing-masing dikhususkan untuk bagian kode tertentu. Bahkan untuk pernyataan kelengkapan pencarian interleaving (dan ini adalah salah satu keuntungan paling penting dari miniKanren atas Prolog standar), tidak mungkin untuk menemukan kata-kata yang ketat. Anda tidak bisa hidup seperti itu, kami memutuskan, dan, setelah menerima berkah dari Will, kami mulai bekerja.

Biarkan saya mengingatkan Anda bahwa semantik yang kami kembangkan pada tahap sebelumnya memiliki batasan yang signifikan: hanya program dengan pencarian terbatas yang dijelaskan. Di miniKanren, menjalankan program juga menarik karena mereka dapat mendaftar dengan jumlah jawaban yang tak terbatas. Oleh karena itu, kami membutuhkan semantik yang lebih keren.

Ada banyak cara standar yang berbeda untuk mendefinisikan semantik bahasa pemrograman, kami hanya harus memilih salah satunya dan menyesuaikannya dengan kasus tertentu. Kami menggambarkan semantik sebagai sistem transisi berlabel - satu set keadaan yang mungkin dalam proses pencarian dan transisi antara negara-negara ini, beberapa di antaranya ditandai, yang berarti bahwa pada tahap pencarian ini, jawaban lain ditemukan. Eksekusi program tertentu dengan demikian ditentukan oleh urutan transisi tersebut. Urutan-urutan ini dapat terbatas (datang ke keadaan terminal) atau tidak terbatas, menggambarkan secara simultan mengakhiri dan tidak menyelesaikan program. Untuk benar-benar menentukan objek seperti itu secara matematis, kita perlu menggunakan definisi koinduktif.

— . , (, , — ..). , miniKanren' ( ).

, , — . . ( ), , .
( ): , , , .

, , / .

Coq'a. , , «. Qed». .

Pemrograman relasional: rasa sakit, minat, dan rasa sakit lagi