🤜🏾 💷 🔴 Wolfensteiny 3D - rekayasa balik 251 byte JavaScript 🚆 👋🏾 🍇

Saat menulis kode, banyak yang tidak memikirkan apa pun selain logika program itu sendiri. Lebih sedikit orang berpikir tentang mengoptimalkan kode dari waktu ke waktu, dari memori. Tetapi hanya beberapa yang mencapai level terakhir - mengompres program ke ukuran kecil.

Misalnya, lihat pada hasil JavaScript hanya 251 byte :

Baiklah, mari kita cari tahu cara kerjanya!

Dari mana asalnya?

Kode ini, serta banyak hal yang saya bahas dalam artikel ini, terdapat di situs p01.org dari Henri Mathieu 'p01' yang luar biasa, seorang pengembang JavaScript dan tidak hanya sering terlibat dalam mengompresi kode ke ukuran yang tidak mungkin. Bahan sumber artikel ini ada di sini .

Jadi, sebelum Anda adalah 251 byte kode sumber.

<body onload=E=c.getContext("2d"),setInterval(F="t+=.2,Q=Math.cos;c.height=300;for(x=h;x--;)for(y=h;y--;E.fillRect(x*4,y*4,bd?4:D/2,D/2))for(D=0;'.'<F[D*y/hD/2|0?1:(d=t+D*Q(T=x/h-.5+Q(t)/8)&7)|(3.5+D*Q(T-8))<<3]&&D<8;b=d)D+=.1",t=h=75)><canvas id=c>

Jelas bahwa tidak ada yang jelas.

Membuat kode dapat dibaca

Pertama-tama, saya mengeluarkan semua kode JavaScript dalam tag yang terpisah, untuk kenyamanan.

Dapat dilihat bahwa variabel E , h , Q , F dan lainnya adalah konstanta yang dapat diganti dengan nilai / objek mereka sendiri, serta mengubah nama.

 var context = c.getContext("2d") var F="t+=.2,Q=Math.cos;c.height=300;for(x=h;x--;)for(y=h;y--;E.fillRect(x*4,y*4,bd?4:D/2,D/2))for(D=0;'.'<F[D*y/hD/2|0?1:(d=t+D*Q(T=x/h-.5+Q(t)/8)&7)|(3.5+D*Q(T-8))<<3]&&D<8;b=d)D+=.1" var t = 75 var size = 75 function render(){ t += 0.2; c.height=300; for(let x = size; x--;) for(let y = size; y--; context.fillRect(x * 4,y * 4,b - d? 4 : D / 2, D / 2)) for(var D = 0; '.' < F[D * y / size - D / 2 | 0 ? 1 : (d = t + D * Math.cos(T = x / size - 0.5 + Math.cos(t) / 8) & 7) | (3.5 + D * Math.cos(T - 8)) << 3] && D < 8; b = d) D += 0.1 } setInterval(render, 75);

Di sini, kode dari string telah diambil ke fungsi, dan string itu sendiri tidak tersentuh, kita akan membutuhkannya di masa depan.

Sekarang konversikan kedua loop luar ke while .

 function render(){ t += 0.2; c.height=300; let x = size; while(x > 0){ let y = size; while(y > 0){ for(var D = 0; '.' < F[D * y / size - D / 2 | 0 ? 1 : (d = t + D * Math.cos(T = x / size - 0.5 + Math.cos(t) / 8) & 7) | (3.5 + D * Math.cos(T - 8)) << 3] && D < 8; b = d) D += 0.1 context.fillRect(x * 4,y * 4,b - d? 4 : D / 2, D / 2); y--; } x--; } }

Bagaimana kita melihat ini?

Mari kita mengerti mengapa kita melihatnya sama sekali. Jika Anda melihat gambar lagi, Anda bisa mengerti banyak.

Gambar yang dapat diklik

Inilah yang kami lihat:

Semakin jauh subjek, semakin gelap subjeknya
Bagian miring dari hambatan yang ditemui dibanjiri secara berbeda dengan garis, bukan titik.

Dalam kode tersebut, gambar tercermin seperti ini:

 // ,  ,       //   ||     // | | || | | // ↓ ↓ ↓↓ ↓ ↓ context.fillRect(x * 4,y * 4,b - d? 4 : D / 2, D / 2);

Mengapa kita melihat benda-benda volumetrik dalam banjir titik-titik hitam ini? Bagaimanapun, kita harus puas dengan hanya nuansa hitam yang berbeda - ukuran titik-titik hitam (kita tidak dapat mengubah warna, E.fillStyle terlalu panjang!). Bahkan, ia bekerja hanya karena dalam gambar dua dimensi, mata kita bergantung terutama pada bayangan dan kecerahan cahaya.

Bayangkan diri Anda berjalan di sepanjang koridor gelap dengan hanya senter di tangan Anda. Anda bersinar di depan Anda dan melihat bahwa beberapa objek lebih dekat dan lebih terang (senter bersinar, hambatan terang, tidak ada bayangan), sementara yang lain lebih jauh dan lebih gelap (cahaya tersebar, lemah, dan kami melihat kegelapan - dan kami merasakan jarak). Jadi di sini - semakin jauh objek ( D lebih besar), semakin besar ukurannya kita menggambar kotak hitam di layar.
Tetapi bagaimana kita tahu apa yang harus cerdas dan mana yang tidak?

Hitung pikselnya

Sekarang mari kita berurusan dengan monster ini:

 for(var D = 0; '.' < F[D * y / size - D / 2 | 0 ? 1 : (d = t + D * Math.cos(T = x / size - 0.5 + Math.cos(t) / 8) & 7) | (3.5 + D * Math.cos(T - 8)) << 3] && D < 8; b = d) D += 0.1

Jadi Semua ungkapan ini adalah algoritme langkah-langkah raymarching yang tetap yang memungkinkan Anda menemukan persimpangan balok dengan balok. Untuk setiap piksel layar, kami meluncurkan sinar, dan kami mengikutinya dengan langkah tetap 0.1 , dan segera setelah kami menemui rintangan, kami menyelesaikan algoritme dan menggambar piksel di layar, mengetahui jarak ke rintangan.

Mari kita mulai membaca kode ini di beberapa bagian.

Kondisi D * y / size - D / 2 | 0 D * y / size - D / 2 | 0 dapat direpresentasikan sebagai

D * (f r a c y s i z e - f r a c 12) = D * (f r a c y - s i z e / 2 s i z e) < 1

$D * (\ frac {y} {size} - \ frac {1} {2}) = D * (\ frac {y - size / 2} {size}) <1$ , maka ekspresi dalam tanda kurung akan menunjukkan "penyimpangan" y dari tengah layar (dalam fraksi layar). Jadi kami mencoba memahami apakah balok itu antara lantai dan langit-langit atau tidak. Karena itu, jika kita menyentuh lantai (atau langit-langit), kita keluar dari loop lebih jauh, untuk menggambar, dan menggambar piksel.
Dan jika kami tidak menyentuh, maka kami melanjutkan perhitungan: kami mencari koordinat balok saat ini.

 var T = x / size - .5 + Math.cos(t) / 8; // Math.cos(t)   //    var xcoord = t + depth * Math.cos(T); var ycoord = 3.5 + depth * Math.cos(T - 8); //

Kenapa cos (T - 8)?

Jadi ternyata begitu

c o s (x - 8) a p p r o x s i n (x)

$cos (x-8) \ approx sin (x)$ dengan akurasi 0,15 radian. Semua karena

f r a c 5 p i 2 s e k i t a r 8.15 s e k i t a r 8

$\ frac {5 \ pi} {2} \ sekitar 8.15 \ sekitar 8$

dan kemudian

c o s (a l p h a - 8) a p p r o x c o s (a l p h a - f r a c 5 p i 2) = c o s (a l p h a - f r a c p i 2) = s i n (a l p h a)

$cos (\ alpha-8) \ approx cos (\ alpha- \ frac {5 \ pi} {2}) = cos (\ alpha - \ frac {\ pi} {2}) = sin (\ alpha)$

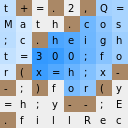
Ada baiknya berbicara tentang bagaimana suatu titik dalam ruang diperiksa untuk suatu blok secara umum. Kartu itu sendiri diambil dari kode sumber ( F ) dan terlihat seperti ini:

 t+=.2,Q= ----> ░█░█░█░░ Math.cos ----> ░░░░█░░░ ;c.heigh ----> ░░█░░░░░   - t=300;fo ----> ░░░░░░░░ <----  , r(x=h;x- ----> ░█░░░░░█     -;)for(y ----> █░█░░░█░ =h;y--;E ----> ░░░░██░░ .fillRec ----> █░░░░░░░

Jadi sepertinya bergerak, bidang pandang kamera ditunjukkan di sini.

Sel-sel yang kode simbolnya kurang dari kode titik - "." Ditandai gelap "." - yaitu, karakter !"#$%&'()*+,-. Sekarang kita kumpulkan koordinat balok, dan coba cari tahu apakah huruf dalam" koordinat "ini gelap (hambatan) atau tidak (kita menerbangkan balok lebih jauh).

Karena indeksnya satu, dan koordinatnya dua, maka kami menggunakan retasan:

 var boxIndex = xcoord & 7 | ycoord << 3;

Akibatnya, kami mendapatkan nomor yang mencerminkan nomor blok (baik, atau kosong).

Ayo kembali ke kode. Sekarang dia terlihat sopan.

Kode ini sedikit gemuk

 function render(){ t += 0.2; c.height=300; let x = size; while(x > 0){ let y = size; while(y > 0){ var depth = 0 while(depth < 8){ depth += 0.1 var T = x / size - .5 + Math.cos(t) / 8; //   var isFloorOrCeiling = depth * y / size - depth / 2 | 0; //      ? if(isFloorOrCeiling) break; var xcoord = t + depth * Math.cos(T) & 7; var ycoord = 3.5 + depth * Math.sin(T); // cos - 8 -> sin boxIndex = xcoord | ycoord << 3; //     , //    if ('.' >= F[boxIndex]) break; b = xcoord; //  ?  ! } context.fillRect(x * 4, y * 4, b - xcoord ? 4 : depth / 2, depth / 2) y--; } x--; } }

Kembali ke menggambar

Mengapa kita membutuhkan semua ini? Sekarang, setelah menjalankan algoritma ini, kita tahu jarak ke objek, dan kita bisa menggambarnya. Tetapi satu pertanyaan tetap tidak terjawab: bagaimana membedakan langit-langit dari unit yang terpisah? Lagi pula, jarak ke langit-langit dan ke blok adalah angka yang tidak berbeda! Sebenarnya, kami sudah menjawab pertanyaan ini.

 // ,  ,      // || // ↓↓ context.fillRect(x * 4, y * 4, b - xcoord ? 4 : depth / 2, depth / 2);

Ada satu syarat dalam kode yang terkait dengan variabel b , dan mempengaruhi lebar "piksel hitam besar": b - xcoord ? 4 : depth / 2 b - xcoord ? 4 : depth / 2 . Mari kita hapus kondisi ini dan lihat apa yang terjadi tanpa itu:

Tidak ada batas antara blok dan langit-langit! (dapat diklik)

Kondisi b - xcoord akan memberi kita lebar konstan ketika perubahan koordinat adalah 0. Dan kapan ini tidak bisa terjadi? Ini tidak terjadi hanya ketika kita tidak mendapatkan (2) baris dalam kode:

 // .... var xcoord = t + depth * Math.cos(T) & 7; // <---    (1) // ... if ('.' >= F[boxIndex]) // <---    (3) break; b = xcoord; // <---     (2) // ....

Ini berarti bahwa program keluar dari siklus sebelumnya, pada baris (3) , ketika balok masuk ke blok buram ke arah yang hampir tegak lurus dengan dindingnya, yaitu jatuh ke "wajah" wajah blok. Dengan demikian, semua balok berbeda dari lantai dan langit-langit.

Jadi, ini adalah bagaimana gambar 3D yang indah ini ternyata, yang tidak hanya menyenangkan mata, tetapi juga membuat Anda berpikir bagaimana dan mengapa itu bekerja. Anda dapat melihat kode ini beraksi di sini (tidak aktif. Situs pengembang keajaiban ini).

Wolfensteiny 3D - rekayasa balik 251 byte JavaScript

Membuat kode dapat dibaca

Bagaimana kita melihat ini?

Hitung pikselnya

Kembali ke menggambar

More articles: