Pada 1974, ahli matematika Inggris Roger Penrose menciptakan satu set ubin revolusioner yang dapat digunakan untuk mengisi bidang tanpa batas dengan pola yang tidak pernah berulang. Pada tahun 1982, ahli kristalografi Israel Daniel Shekhtman menemukan sebuah logam campuran yang atom-atomnya disusun dalam urutan yang belum pernah ditemukan sebelumnya dalam ilmu material. Penrose mencapai pengakuan publik besar-besaran, jarang diberikan kepada ahli matematika. Shekhtman menerima Hadiah Nobel. Kedua ilmuwan menantang intuisi manusia dan mengubah dasar-dasar memahami struktur alam, menemukan bahwa variabilitas tak terbatas dapat terjadi bahkan dalam lingkungan yang sangat teratur.
Inti dari penemuan mereka adalah "simetri terlarang," yang disebut demikian karena bertentangan dengan hubungan yang mengakar antara simetri dan pengulangan. Simetri didasarkan pada sumbu refleksi - semua yang ada di satu sisi garis diduplikasi di sisi lain. Dalam matematika, hubungan ini diungkapkan oleh pola ruang ubin. Bentuk simetris, seperti persegi panjang dan segitiga, dapat mengisi bidang tanpa celah dan overlay, menciptakan pola yang terus berulang. Pola berulang disebut "periodik" dan mereka dikatakan memiliki "transfer simetri". Jika Anda memindahkan pola (pola) dari satu tempat ke tempat lain, itu akan terlihat sama.
Sebagai ilmuwan yang berani dan ambisius, Penrose lebih tertarik bukan pada pola dan pengulangan yang sama, tetapi pada variabilitas tanpa batas. Lebih khusus lagi, ia tertarik pada ubin "aperiodik", yaitu, set angka yang dapat mengisi bidang tanpa batas tanpa celah dan overlay, dan pola ubin tidak pernah diulang. Ini adalah tugas yang sulit karena dia tidak dapat menggunakan angka (ubin) dengan dua, tiga, empat atau enam sumbu simetri - persegi panjang, segitiga, kotak atau segi enam - karena pada pesawat tak terbatas mereka akan membuat pola periodik atau berulang. Artinya, dia perlu menggunakan figur yang dianggap meninggalkan celah saat mengisi pesawat - figur yang telah melarang simetri.
Untuk membuat bidangnya sendiri dari pola-pola yang tidak berulang, Penrose beralih ke simetri lima sumbu - ke pentagon, khususnya karena, menurutnya, “hanya menyenangkan untuk melihat pentagon”. Hal yang luar biasa tentang sosok Penrose adalah bahwa meskipun ia mendapatkan angka-angka ini dari garis dan sudut persegi panjang, mereka tidak meninggalkan celah jelek. Mereka saling menempel erat, menekuk dan memutar pesawat, selalu dekat dengan pengulangan, tetapi tidak pernah mencapainya.
Mosaik Penrose telah menarik perhatian publik karena dua alasan utama. Pertama, ia menemukan cara untuk menghasilkan pola yang berubah tak terbatas hanya dari dua jenis bentuk. Kedua, ubinnya sederhana, sosok simetris, yang dalam dirinya sendiri tidak menunjukkan tanda-tanda sifat yang tidak biasa.

Penrose menciptakan beberapa varietas dari set figur aperiodiknya. Salah satu yang paling terkenal disebut "ular" dan "panah". "Layang-layang" terlihat seperti layang-layang anak-anak, dan "panah" terlihat seperti garis besar pembom siluman yang disederhanakan. Keduanya jelas dibagi sepanjang sumbu simetri dan masing-masing memiliki busur simetris sederhana di permukaan. Penrose menetapkan satu aturan untuk menempatkan bentuk: untuk penempatan ubin yang "tepat", busur ini harus cocok, menciptakan kurva yang tidak dapat dipisahkan. Tanpa aturan ini, "ular" dan "panah" dapat diatur dalam pola berulang. Jika Anda mengikuti aturan ini, maka pengulangan tidak pernah terjadi. "Snake" dan "dart" mengisi pesawat tanpa batas, menari di sekitar lima kapak mereka, menciptakan bintang dan dekagon, kurva melengkung, kupu-kupu, dan bunga. Angka-angka diulang, tetapi variasi baru muncul di dalamnya.
Profesor klinis matematika Edmund Harriss dari University of Arkansas, yang menulis gelar doktor tentang ubin Penrose, menawarkan perbandingan semacam itu. "Bayangkan bahwa Anda hidup di dunia kotak. Anda mulai berjalan, dan ketika Anda sampai di ujung alun-alun, yang berikutnya persis sama, dan Anda tahu apa yang akan Anda lihat jika Anda terus bergerak tanpa henti. " Ubin Penrose memiliki sifat yang persis berlawanan. “Informasi apa pun yang Anda miliki, bagian apa pun dari pola yang Anda lihat, Anda tidak akan pernah bisa memprediksi apa yang akan terjadi selanjutnya. Akan selalu ada sesuatu yang belum Anda lihat sebelumnya. "
Salah satu aspek aneh dari pemisahan aperiodik sebuah pesawat adalah bahwa informasi penentuan posisi entah bagaimana ditransmisikan dari jarak jauh - ubin Penrose, diletakkan di satu tempat, mencegah penempatan ubin lain di ratusan (dan juga ribuan dan jutaan) ubin darinya. “Kendala lokal entah bagaimana menciptakan kendala global,” kata Harriss. "Ini menunjukkan bahwa pada skala apa pun ubin ini tidak akan membuat apa pun secara berkala." Anda mungkin memiliki pilihan untuk menempatkan, misalnya, "ular" di satu daerah, atau "panah" di tempat terpencil. Salah satu ubin akan melakukan, tetapi tidak keduanya.
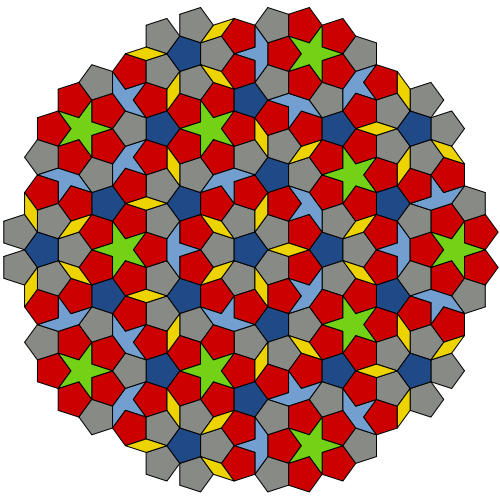
Ubin ini, membentuk pola yang tak berujung dan tidak berulang, mengungkapkan rasio Fibonacci, juga dikenal sebagai "rasio emas". Dua angka dikatakan memiliki rasio emas jika rasio angka yang lebih kecil ke yang lebih besar sama dengan rasio angka yang lebih besar dengan jumlah dua angka. Dalam hal ini, rasio area "ular" dengan area "panah" adalah rasio emas. Rasio sisi panjang "ular" dengan sisi pendeknya juga rasio emas.
Ubin Penrose juga dapat dibagi lagi menjadi versi yang lebih kecil. "Ular" terdiri dari dua "ular" yang lebih kecil dan dua bagian "anak panah". "Panah" terdiri dari "ular" yang lebih kecil dan dua karpet "panah". (Dalam setiap ubin Penrose yang tepat, bagian dari "panah" ini disejajarkan satu sama lain. Dari sudut pandang matematika, ini memungkinkan mereka untuk dianggap sebagai keseluruhan "panah.") "Misalkan kita memiliki sepotong mosaik Penrose yang terdiri dari" ular "dan" panah "B "Kata Harriss. "Jika saya membagi mereka, saya akan mendapatkan 2" ular "
A +
B , dan" panah ""
A +
B. "
Jika Anda melakukan penggantian ini beberapa kali, maka Anda dapat menghitung bagian total dari setiap jenis ubin, seolah-olah diletakkan pada bidang yang tak terbatas. Dalam perhitungan seperti itu, pola
berulang selalu mengarah ke bilangan rasional. Jika proporsinya adalah bilangan irasional, maka ini berarti bahwa polanya tidak akan pernah benar-benar berulang. Dalam perhitungan untuk ubin Penrose, tidak hanya angka irasional yang diperoleh, rasio mereka adalah rasio Fibonacci - rasio "panah" ke "ular" sama dengan rasio "ular" dengan jumlah ubin.
Mengingat bahwa proporsi Fibonacci itu ada di mana-mana di alam - dari nanas ke populasi kelinci - bahkan lebih aneh bahwa proporsi ini mendasar bagi sistem ubin, yang, tampaknya, tidak ada hubungannya dengan dunia fisik. Penrose menciptakan sesuatu yang baru dalam sains, menarik di sana bahwa itu seharusnya tidak bekerja seperti yang dilakukan alam. Itu seperti Penrose menulis cerita fiksi ilmiah tentang spesies hewan baru, dan kemudian ahli zoologi menemukan spesies ini hidup di Bumi. Faktanya, ubin Penrose dikaitkan dengan rasio emas, dengan matematika yang kami temukan, dan matematika dunia di sekitar kita.

Mengambil studi tentang simetri terlarang, Penrose tidak dapat menduga bahwa ia telah menjadi bagian dari pergeseran pemikiran yang mengarah pada penemuan bidang baru ilmu matematika. Lagi pula, simetri merupakan hal mendasar bagi matematika murni dan dunia alami. Ahli astrofisika Mario Livio menyebut simetri "salah satu alat yang paling penting untuk menguraikan struktur alam." Alam menggunakan kuadrat dan segi enam untuk alasan yang sama seperti manusia: mereka sederhana, efisien, dan teratur. Jika segilima tampak tidak praktis bahkan untuk tugas sederhana seperti mengisi ubin lantai dalam desain interior, maka, tentu saja, diyakini bahwa mereka tidak dapat digunakan untuk membuat atom dalam bahan padat seperti kristal.
Kristal terdiri dari kisi atom tiga dimensi. Kristal tumbuh dengan menambahkan atom baru dan memperluas kisi-kisi. Ini terjadi paling efisien ketika atom berbaris dalam pola berulang. Selama beberapa dekade, sejarah berakhir di sana: kristal mengulangi struktur. Intinya.
Tetapi kemudian, pada tahun 1982, Shekhtman pergi cuti kreatif dari Universitas Technion di Haifa dan mulai bekerja di National Bureau of Standards. Dia meraba-raba di laboratorium paduan aluminium-mangan. Pola difraksi yang diciptakan oleh struktur kristalinnya tampaknya tidak menyerupai salah satu dari kesimetrian standar yang diketahui oleh para ahli kristalografi. Faktanya, atom-atom berjajar dalam segi lima, rhombus, “ular” dan “panah” yang ditemukan Penrose dalam dunia matematika.
"Tentu saja, saya kenal dengan ubin Penrose," kata Schechtman. Tapi dia tidak punya alasan untuk mencurigai hubungan mereka dengan paduan ini. “Saya tidak mengerti apa itu. Selama bulan-bulan berikutnya, saya mengulangi percobaan saya berulang kali. Pada akhir liburan kreatif saya, saya tahu persis apa yang bukan, tetapi saya masih belum tahu apa itu. "
Untuk memahami apa yang dia temukan, Schechtman, seperti Penrose, harus mempertanyakan ide-ide intuitifnya yang biasa. Dia harus menerima simetri terlarang dan kebingungan pentagonal dengan kurangnya pengulangan. Sementara di Israel, ia enggan mengakui bahwa ia telah menemukan struktur atom kristal kristalin yang tidak berulang. Namun, tidak ada seorang pun di dunia sains material yang pada awalnya dapat menghubungkan penemuan ini dengan kristal. Oleh karena itu, mereka disebut "kristal quasicry."
Matematika aneh Penrose tampaknya telah menembus ke dunia alami. "Selama 80 tahun, kristal telah didefinisikan sebagai struktur" teratur dan berkala ", karena semua kristal yang kami pelajari sejak 1912 adalah berkala," jelas Schechtman. “Barulah pada tahun 1992 bahwa International Union of Crystallographers mengorganisir sebuah komite untuk memilih definisi baru untuk kata crystal. Definisi baru ini adalah perubahan paradigma untuk kristalografi. "
Bukan hanya kelambanan berpikir sederhana yang mencegah pemahaman Shekhtman dan penerimaan penemuan. Struktur kristal aperiodik bukan hanya asing - mereka dianggap tidak alami. Ingatlah bahwa lokasi satu ubin Penrose dapat memengaruhi bentuk dalam ribuan ubin darinya - pembatasan lokal membuat yang global. Tetapi jika kristal terbentuk atom demi atom, maka seharusnya tidak ada hukum alam yang menciptakan batasan yang melekat pada ubin Penrose.
Ternyata kristal tidak selalu membentuk atom demi atom. “Dalam senyawa intermetalik yang sangat kompleks, unsur-unsurnya sangat besar. Mereka bukan lokal, ”kata Schechtman. Ketika fragmen kristal besar terbentuk pada saat yang sama, alih-alih oleh pertumbuhan atom secara bertahap, atom yang terletak sangat jauh dari satu sama lain dapat mempengaruhi posisi bersama, seperti pada ubin Penrose.
Seperti halnya banyak tabu, simetri terlarang telah diakui sebagai salah satu bentuk keberadaan yang dapat diterima di alam. Quasicrystals tidak hanya menjadi objek studi dalam bidang baru penelitian ilmiah: ternyata mereka memiliki banyak sifat berguna yang muncul karena strukturnya yang tidak biasa. Sebagai contoh, konfigurasi atom asimetris mereka memberi mereka energi permukaan rendah, yaitu, sedikit yang bisa menempel padanya. Dengan demikian, pelapis quasicrystalline mulai digunakan dalam peralatan dapur non-stick. (Ketika Penrose membuat ubin baru, dia tidak bisa membayangkan bahwa mereka akan digunakan dalam kristalografi, belum lagi menggoreng telur.) Selain itu, quasicrystals biasanya memiliki gesekan dan keausan rendah, sehingga mereka merupakan pelapis yang ideal untuk pisau cukur dan bedah. instrumen, atau instrumen tajam lainnya yang berkaitan dengan tubuh manusia.

Karena struktur quasicrystal tidak pernah diulang, mereka menciptakan pola difraksi unik dari radiasi elektromagnetik. Para peneliti Photonics tertarik pada bagaimana mereka mempengaruhi transmisi cahaya, reflektifitas, dan photoluminescence. Jika mereka didinginkan, maka hambatan listrik mereka turun ke level hampir nol. Tetapi mereka juga menyerap radiasi inframerah, sehingga mereka memanaskan dengan sangat cepat ke suhu tinggi. Karena itu, mereka menjadi tambahan yang sangat berguna untuk printer 3D, di mana bubuk plastik digunakan sebagai bahan awal. Shekhtman menjelaskan: jika bubuk quasi periodik dicampur dengannya dan terkena radiasi infra merah, maka bubuk quasi periodik "memanas dengan sangat cepat dan melelehkan partikel plastik di sekitarnya, yang membuat mereka saling menempel."
Tidak ada yang tahu bagaimana kisah simetri terlarang berakhir. Matematikawan terus mengeksplorasi sifat-sifat ubin Penrose. Quasicrystals tetap menjadi subjek studi dalam penelitian fundamental dan terapan. Namun sejauh ini perjalanan ini luar biasa. Selama 40 tahun terakhir, simetri lima sumbu telah berubah dari tidak praktis menjadi bernilai, dari tidak alami menjadi sepenuhnya alami, dari terlarang menjadi dominan. Dan untuk transformasi ini, kita harus berterima kasih kepada dua ilmuwan yang meninggalkan ide-ide mereka yang biasa untuk menemukan bentuk baru yang luar biasa dari variasi alam yang tak berkesudahan.
Tentang Penulis: Patchen Bars adalah jurnalis dan penulis yang tinggal di Toronto. Dia saat ini sedang mengerjakan sebuah buku tentang hubungan antara matematika murni dan alam.