Fraktal dalam bilangan irasional

Artikel ini merupakan kelanjutan dari artikel pertama saya , Fractals in Prime Numbers .

Artikel selanjutnya: Fraktal dalam bilangan irasional. Bagian 2



Dalam artikel sebelumnya, kami belajar cara menggambar pola yang mirip diri sendiri dengan menggunakan bilangan prima yang saling menguntungkan. Pada artikel ini saya akan menunjukkan sifat fraktal dari angka tersebut $$$\ sqrt {2}$ .
Tanpa kata pengantar. Di bawah kucing.

Kami akan mendefinisikan terminologi dan notasi. Dalam matematika, sistem yang dijelaskan di bawah ini disebut biliar . Selanjutnya kita akan menggunakan istilah ini. Dimensi biliar persegi panjang akan dilambangkan dengan $$$M$ (lebar) dan $$$N$ (tinggi).

Biliar biner

Pada artikel sebelumnya, kami mengambil biliar persegi dengan sisi $$$M$ dan $$$N$ , meluncurkan bola ke dalamnya dan menandai lintasan dengan garis putus-putus melalui sel:



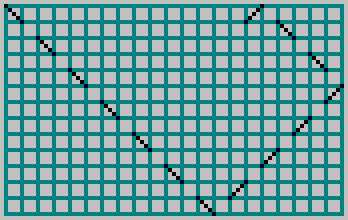
Untuk saling sederhana $$$M$ dan $$$N$ kita mendapatkan polanya:



Dalam versi biner, kami menandai lintasan tidak dengan garis putus-putus, tetapi secara bergantian mengecat sel dengan hitam dan putih (kami membentuk array biner, menempatkan 0 untuk hitam dan 1 untuk putih di sel yang sesuai):



Aturan Refleksi Perbatasan:



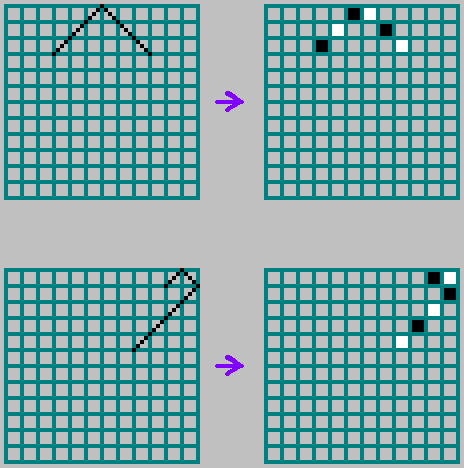
Untuk saling sederhana $$$M$ dan $$$N$ lintasan melewati setiap sel:




Jika para pihak memiliki pembagi umum, maka bola memasuki sudut sebelum melewati setiap sel:



Lebih mudah untuk menganggap kasus ini sebagai biliar dalam persegi panjang dengan sisi $$$\ frac {M} {GCD}$ dan $$$\ frac {N} {GCD}$ (GCD adalah faktor umum terbesar):



Sebelum melanjutkan, isi tabel yang diusulkan oleh pengguna Captain1312 dalam artikelnya (kami akan membagi sisi biliar menjadi GCD).

$$$(1, 0)$ sedikit

Untuk setiap meja biliar $$$M$ dan $$$N$ ambil sedikit dengan koordinat $$$(1, 0)$ .



Jika $$$M$ adalah pembagi $$$N$ - lalu sedikit dengan koordinat $$$(1, 0)$ hilang ( $$$\ frac {M} {GCD} = 1$ ) Dalam hal ini, kami mengambil bit terbalik dengan koordinat $$$(0, 1)$ .

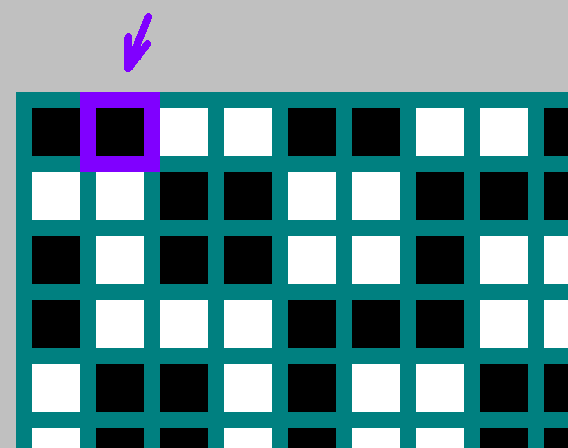
Isi tabel. Asalnya adalah sudut kiri atas. Oleh $$$x$ - lebar biliar $$$M$ oleh $$$y$ - tinggi $$$N$ . Untuk setiap biliar, kami menandai sedikit $$$(1, 0)$ , atau bit terbalik $$$(0, 1)$ (kami akan kembali ke topik ini di bawah).

Urutan biner

Kenapa kami membalikkan bit ketika lebar biliar $$$M = 1$ ? Untuk saling sederhana $$$M$ dan $$$N$ , lintasan bola melewati masing-masing sel. Di antara dinding atas dan kiri biliar, bola setiap kali melewati jumlah sel yang genap.





Bit di kolom kiri adalah bit terbalik dari baris atas. Kami tidak mengambil bit nol - lintasan dimulai dengan itu:



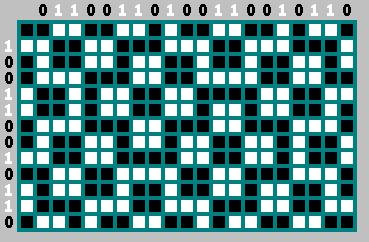
Selain itu, kami dapat dengan aman membuang setiap bit kedua dari urutan ini (bit $$$2_ {n-1}$ - bit terbalik $$$2_ {n}$ ):



Dapat urutannya $$$10 100 110 110$ untuk biliar $$$(21,13)$ . Urutannya unik untuk semua orang. $$$M$ dan $$$N$ .

Apa pun tingginya $$$N$ kami tidak mengambil - bola selalu berjalan di sepanjang lintasan $$$2N$ antara dua pantulan dari dinding atas. Dari dinding atas, gerakan selalu dimulai dengan bit “0” (sel hitam) dan berakhir dengan bit “1” (sel putih):



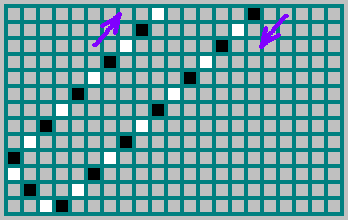
Bahkan, urutan (yang kami soroti di atas - $$$10 100 110 110$ ) menunjukkan di sisi mana bola terbang: 1 - jika bola terbang, tercermin dari dinding kanan dan 0 - jika bola terbang, tercermin dari dinding kiri. Dalam gambar, lintasan bola ditandai hitam jika bola bergerak ke kanan dan putih jika bergerak ke kiri:




Urutan ini ( $$$10 100 110 110$ ) berisi semua informasi yang diperlukan tentang pola. Dengan itu, kita dapat mengembalikan pola asli (dan bahkan melihat di luar batas bawah pola). Ambil bujur sangkar dengan sisi $$$M$ . Kami mengatur bit urutan kami di tempat-tempat di mana bola menabrak dinding atas (jarak antara sentuhan berdekatan bola adalah 2 sel).



Jika bit yang sesuai = 1 - kita mulai bergerak ke kiri, menandai lintasan melalui sel. Jika bit = 0 - pindah ke kanan.



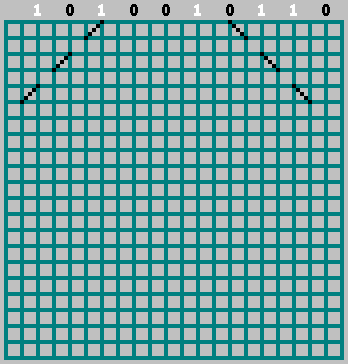
Dalam hal ini, jangan lupa tentang bit nol:



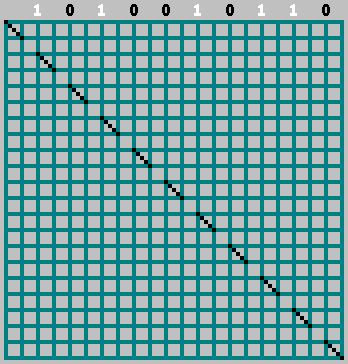
Gif:



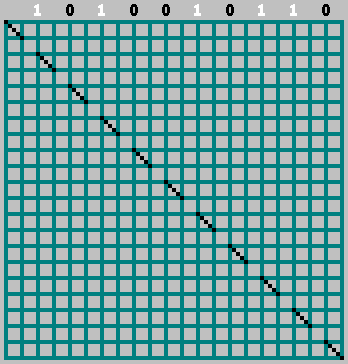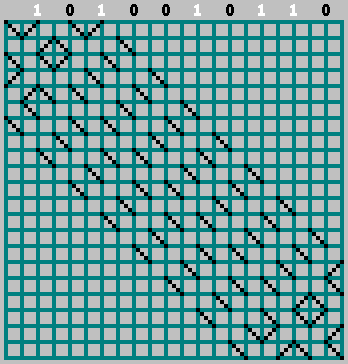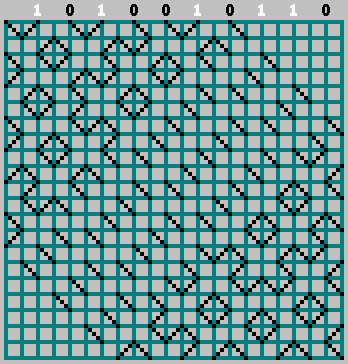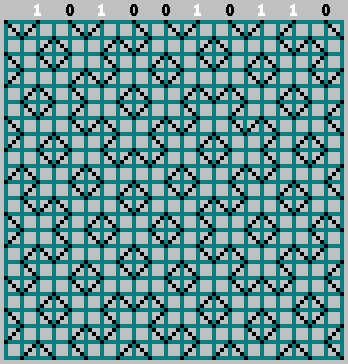
Kami mendapatkan pola aslinya (dan melihat sedikit melewati batas bawah):



Script untuk memvisualisasikan urutan biner

Kita dapat membangun urutan ini menggunakan sisa divisi.

Biliar satu dimensi

Pada sumbu numerik $$$X$ ambil dua poin: $$$0$ dan $$$M$ .



Bergerak dari satu titik ke titik lainnya, ukur jaraknya $$$N$ :



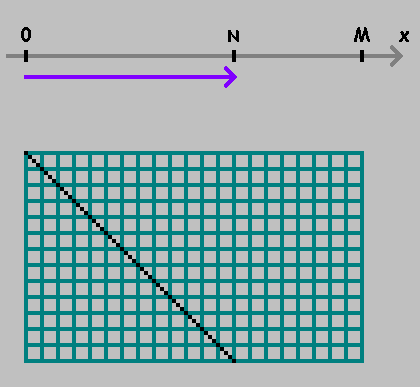
Menandai intinya. Kami terus mengukur jarak dari titik ini, menjaga arah. Jika Anda telah mencapai titik tersebut $$$0$ atau $$$M$ - ubah arah:



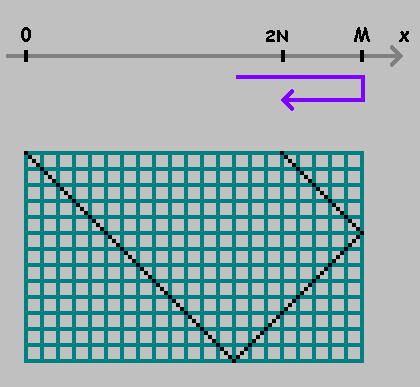
Seperti dapat dilihat pada gambar di atas, titik pertama menunjukkan tempat di mana bola menyentuh dinding bawah biliar. Poin ini tidak menarik bagi kita. Kami hanya akan memperbaiki poin $$$2kN$ untuk $$$k = 0,1,2, ...$ .

Bagaimana cara menandai poin-poin ini? Putar biliar kami pada porosnya $$$X$ . Tandai poinnya $$$0, M, 2M, 3M, ...$ . Sekarang mencapai titik $$$M$ kita tidak mengubah arah gerakan, tetapi terus bergerak ke titik $$$2 juta$ .



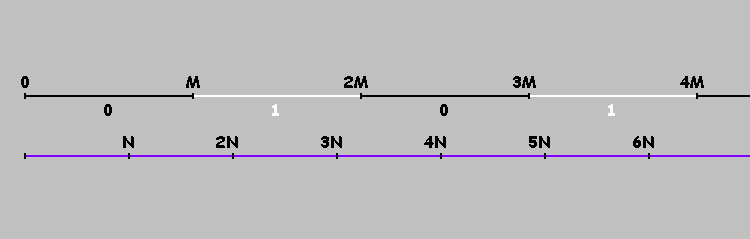
Kelipatan $$$M$ , bagi sumbu kami menjadi beberapa segmen. Kami menandai segmen-segmen ini dengan satu dan nol (berselang-seling). Pada segmen yang ditandai dengan nol, bola (dalam biliar persegi panjang) bergerak dari kiri ke kanan. Di segmen yang ditandai dengan unit - dari kanan ke kiri. Atau lebih sederhana: bola bergerak dari kiri ke kanan jika $$$Q_k = 0$ untuk

$$

$$Q_k = \ lfloor \ frac {2kN} {M} \ rfloor \; (\ textrm {mod} \; 2); \ quad k = 0,1,2, ...$$

(Perhatian khusus harus diberikan pada formula ini. Selanjutnya, kami akan kembali ke sana)

Mudah untuk melihat bahwa titik di mana bola menyentuh dinding atas biliar adalah sisa dari divisi $$$2kN$ pada $$$M$ . Dalam hal ini, kami tidak bisa memperbaiki pergerakan bola ke arah yang berlawanan. Kami mengambil seluruh bagian dari divisi ini $$$2kN$ pada $$$M$ jika itu adil - kami mempertimbangkan sisa divisi $$$2kN$ pada $$$M$ . Membagi sisa yang dihasilkan oleh 2 (jarak antara titik kontak yang berdekatan adalah dua sel). Mendapat indeks elemen array, yang perlu kita isi dengan nol. Elemen yang tersisa diisi dengan unit (bola bergerak dari dinding kanan ke kiri).

Panjang Urutan = $$$\ frac {M} {2}$ .

function sequence(m,n){ var md=m/2; var array=[]; for(var k=0;k<md;k++) array[k]=1; for(var k=0;k<md;k++) if(Math.floor(2*k*n/m)%2==0) array[((2*k*n)%m)/2]=0; return array; } console.log(sequence(55, 34).join('')); // -> 0101001011010010110101101001 

Sekarang kita dapat membangun urutan biner untuk biliar dengan sisi mana saja $$$M$ dan $$$N$ (dengan angka alami).
Beberapa contoh:
144x89 (angka Fibonacci):
010100101101001011010110100101101001010010110100101101011010010110100101

169x70 (nomor Pell):
0101011010100101011010100101011010110101001010110101001010110101001010010101101010010

233x55 (angka Fibonacci aneh $$$F_n$ dan $$$F_ {n-3}$ ):
0100100110110110010011011011001001001101100100100110110010010011011011001001101101100
10010011011001001001101100100100


Kami memiliki urutan. Bagaimana lagi Anda bisa memvisualisasikan urutan biner? Menggunakan Turtle Graphics .

Grafis penyu

Buat garis. Selanjutnya, kami mengambil bit secara bergantian dari urutan kami. Jika bit = 1 - putar segmen relatif ke yang sebelumnya $$$60 ^ {\ circ}$ (searah jarum jam). Jika bit = 0 - ubah segmen dengan $$$-60 ^ {\ circ}$ . Awal segmen berikutnya adalah akhir dari segmen sebelumnya.



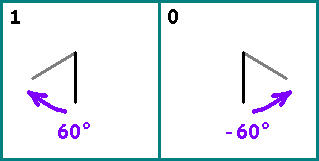
Ambil dua angka Fibonacci yang cukup besar: $$$F_ {29} = 514229$ dan $$$F_ {28} = 317811$ .

Dibangun urutan:
00101101001011010010100101101001011010110100101101001010010110100101 ... (257114 karakter plus bit nol).

Kami memvisualisasikan menggunakan grafis kura-kura. Ukuran segmen awal adalah 10 piksel (segmen awal di sudut kanan bawah):



Ukuran segmen awal adalah 5 piksel:



Ukuran segmen awal adalah 1 piksel:



Contoh selanjutnya adalah nomor Pell.

$$

$$P_n = \ begin {cases} 0, n = 0; \\ 1, n = 1 \\ 2P_ {n-1} + P_ {n-2}, n> 1 \ end {cases}$$

Ambil $$$P_ {16} = 470832$ dan $$$P_ {15} = $ 19502$ .

Urutan:
001010010101101010010101101010010100101011010100101011010100001010110110 (235415 karakter ditambah nol bit).

Ukuran segmen awal adalah 1 piksel:



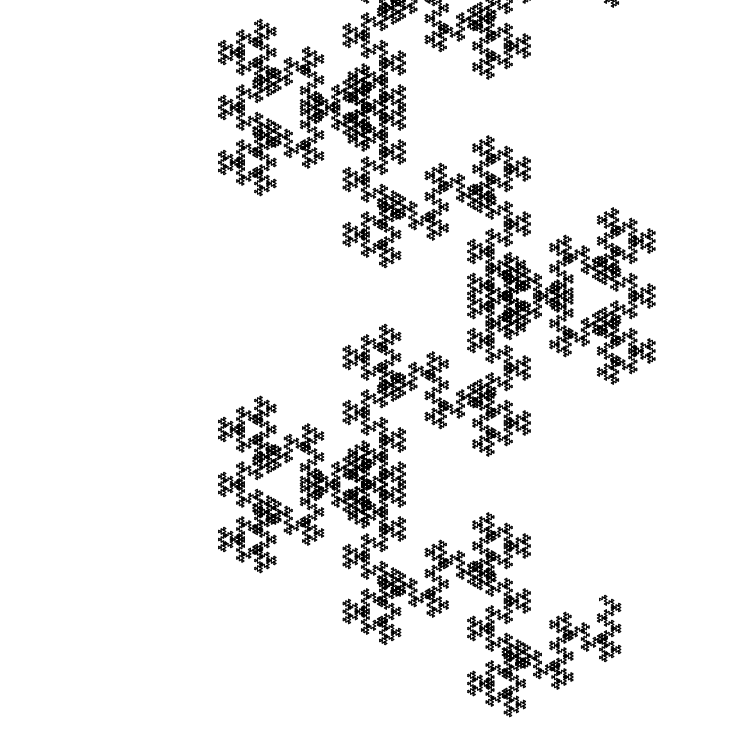
Contoh lain adalah angka Fibonacci aneh $$$F_n$ dan $$$F_ {n-3}$ .
Ambil $$$F_ {28} = 317811$ dan $$$F_ {25} = 75025$ .
Urutan:
00110110010010011111001001001001101101100100110110110010010011011011001001 ... (158905 ditambah sedikit nol).
Alih-alih sudut $$$60 ^ {\ circ}$ dan $$$-60 ^ {\ circ}$ kami akan menggunakan sudut $$$90 ^ {\ circ}$ dan $$$-90 ^ {\ circ}$ .
Ukuran segmen awal adalah 5 piksel:



Ukuran segmen awal adalah 0,4 piksel:



Kurva ini memiliki nama - " Fibonacci word fraktal ". Dimensi Hausdorff untuk kurva ini diketahui:

$$

$$D = 3 {\ frac {\ log \ Phi} {\ log (1 + {\ sqrt {2}})}} = 1.6379; \ quad \ Phi = \ frac {1 + {\ sqrt {5}}} {2}$$

Script untuk memvisualisasikan urutan biner menggunakan Turtle Graphics

Masalah

Mungkinkah menggambar pola untuk biliar, yang sisi-sisinya tidak dapat dibandingkan (salah satu sisinya adalah bilangan irasional)? Tugasnya tidak sepele. Mencoba memecahkan masalah ini, kami akan menghadapi sejumlah pertanyaan:

1. Jika para pihak tidak dapat dibandingkan - kami tidak dapat membuka biliar dengan sel dengan ukuran yang sama.
2. Jika kedua sisi tidak bisa dibandingkan - bola akan memantul tanpa henti dan tidak akan pernah menyentuh sudut.
3. Urutan dalam biliar diisi secara acak, tetapi secara acak.



Dua pertanyaan pertama, jelas, tidak punya solusi. Tetapi jika ada cara untuk mengisi urutan secara berurutan, maka kita bisa, bergerak di sepanjang urutan dari kiri ke kanan, mengembalikan pola dengan cara yang kita gunakan di atas. Dan dengan demikian untuk melihat bagaimana polanya terlihat di sudut kiri atas biliar, sisi-sisinya tidak dapat dibandingkan.

Ilmu hitam

Ambil biliar, yang sisi-sisinya sama dengan angka Fibonacci (dengan angka lain, trik semacam itu mungkin tidak berfungsi). Jalankan bola ke dalamnya dan perbaiki jumlah bola yang menyentuh dinding atas. Isi angka dengan putih - jika bola bergerak dari kanan ke kiri dan hitam - jika bola bergerak dari kiri ke kanan:



Warna putih sesuai dengan satu dalam urutan, hitam - nol. Sekarang mari kita mengatur angka-angkanya:



Kami mendapat urutan yang sama dari nol dan nol.


Bahkan, dalam beberapa kasus, kita tidak perlu mengambil sisa divisi. Untuk bilangan Fibonacci, cukup untuk memeriksa paritas bagian integer dari divisi $$$2kN$ pada $$$M$ :

$$

$$Q_k = \ lfloor \ frac {2kN} {M} \ rfloor \; (\ textrm {mod} \; 2); \ quad k = 0,1,2, ...$$

Dalam pembilang yang kita miliki $$$F_ {n}$ . Dalam penyebut - $$$F_ {n + 1}$ .

Seperti yang Anda ketahui:

$$

$$\ lim_ {n \ to \ infty} \ frac {F_n} {F_ {n + 1}} = \ frac {1} {\ Phi}$$

$$$\ Phi$ - Rasio emas. Bilangan irasional. Sekarang kita dapat menulis rumus kita sebagai:

$$

$$Q_k = \ lfloor \ frac {2k} {\ Phi} \ rfloor \; (\ textrm {mod} \; 2); \ quad k = 0,1,2, ...$$

Kami mendapat formula untuk mengisi urutan biliar, yang lebarnya sama dengan $$$\ Phi$ dan tinggi $$$1$ . Panjang Urutan = $$$\ infty$ , tetapi kita dapat mengembalikan bagian dari pola, bergerak dari kiri ke kanan secara berurutan dan melihat ke sudut kiri atas biliar. Masih mencari cara menghitung $$$\ Phi$

Unit dibagi dengan rasio emas dapat ditulis ulang sebagai:

$$

$$\ frac {1} {\ Phi} = \ frac {-1 + {\ sqrt {5}}} {2}$$

Kita dapat menyingkirkan dua:

$$

$$\ frac {2k} {\ Phi} = \ frac {2k (-1 + {\ sqrt {5}})} {2} = k \ sqrt {5} -k$$

Formula kami berbentuk:

$$

$$Q_k = \ lfloor k \ sqrt {5} -k \ rfloor \; (\ textrm {mod} \; 2); \ quad k = 0,1,2, ...$$

Untuk lebih jelasnya, saya menggambar sebuah meja. Di kolom ketiga, kami membuang bagian fraksional dan meninggalkan keseluruhan. Di kolom keempat, kami memeriksa paritas bagian integer:



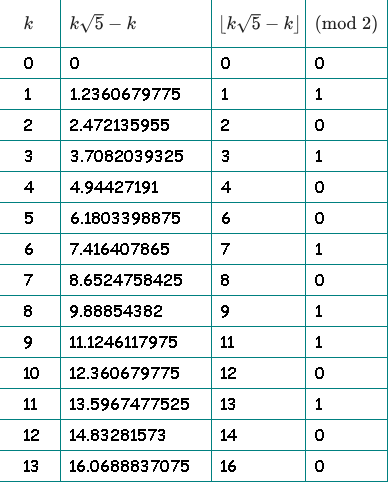
Di kolom keempat kami mendapat urutan kami: 01010010110100 ...

Kami terus menghitung bit untuk sisanya $$$k$ . Memulihkan bagian dari pola biliar dengan sisi $$$1$ dan $$$\ Phi$ :



Jika Anda tidak mengambil setiap waktu $$$k$ - maka setiap bit kedua dalam urutan terbalik. Kami mendapatkan formula umum:

$$

$$Q_k = \ lfloor k \ sqrt {x} \ rfloor \; (\ textrm {mod} \; 2); \ quad k = 0,1,2, ...$$

Apa yang mencegah kita menggunakan akar kuadrat dari tiga atau, katakanlah, dua bukan akar kuadrat dari lima? Tidak ada

Kami membuat urutan untuk $$$k \ sqrt {3} + k$

 var x=3; var q=[]; for(var k=0;k<256000;k++) q[k]=Math.floor(k*Math.sqrt(x)+k)%2; 

Beberapa bit pertama dari urutan:
00100101101001001011010010110110100101101001001011010010010110100101 ...

Kami akan memvisualisasikan menggunakan grafis penyu. Sudut 90 dan -90 derajat. Ukuran segmen awal adalah 5 piksel:



Ukuran segmen awal adalah 0,5 piksel:



Kami membuat urutan untuk $$$k \ sqrt {2}$

 var x=2; var q=[]; for(var k=0;k<256000;k++) q[k]=Math.floor(k*Math.sqrt(x))%2; 

Beberapa bit pertama dari urutan ( A083035 ):
01001101100100110010011011001101100100110110011011001001100100110110 ...

Sudut 90 dan -90 derajat. Ukuran segmen awal adalah 5 piksel:



Ukuran segmen awal adalah 0,5 piksel:





Sudut 60 dan -60 derajat. Ukuran segmen awal adalah 5 piksel:



Script visualisasi

Seseorang mungkin meragukan bahwa paritas bagian bilangan bulat $$$k \ sqrt {2}$ memberikan urutan fraktal. Kami memvisualisasikan bagian dari urutan ini dengan cara kedua:



Untuk lebih jelasnya, saya melukis di atas kurva terpanjang dalam pola yang dihasilkan:



Kurva ini memiliki nama - "Fibonacci word fraktal".

Bagaimana cara mendapatkan urutan ini menggunakan biliar? Kami mengambil biliar, yang lebarnya = 1, dan tinggi = $$$\ sqrt {2}$ . Di batas atas dan bawah, kami memperbaiki arah gerakan bola. Jika bola bergerak dari kiri ke kanan - tulis 0, jika dari kanan ke kiri - tulis 1.



Dua grafik:

$$

$$z = \ lfloor y \ sqrt {x} \ rfloor \; (\ textrm {mod} \; 2)$$

$$

$$z = \ lfloor yx \ sqrt {2} \ rfloor \; (\ textrm {mod} \; 2)$$

Anda dapat melanjutkan dalam nada ini untuk waktu yang sangat lama - pola memiliki banyak sifat menarik. Tetapi artikel itu sudah terlalu rumit. Saya akan menceritakan tentang salah satu properti menarik pada akhirnya.