Selama pengembangan meshoptimizer , pertanyaan sering muncul: "Bisakah algoritma ini menggunakan SIMD?"

Perpustakaan berorientasi pada kinerja, tetapi SIMD tidak selalu memberikan keuntungan kecepatan yang signifikan. Sayangnya, SIMD dapat membuat kodenya lebih mudah dibawa-bawa dan tidak dapat dirawat. Karena itu, dalam setiap kasus, perlu untuk mencari kompromi. Ketika kinerja sangat penting, Anda harus mengembangkan dan memelihara implementasi SIMD terpisah untuk set instruksi SSE dan NEON. Dalam kasus lain, Anda perlu memahami apa efek menggunakan SIMD. Hari ini kami akan mencoba untuk mempercepat penyederhanaan mesh ceroboh, sebuah algoritma baru yang baru-baru ini ditambahkan ke perpustakaan, menggunakan set instruksi SSEn / AVXn.



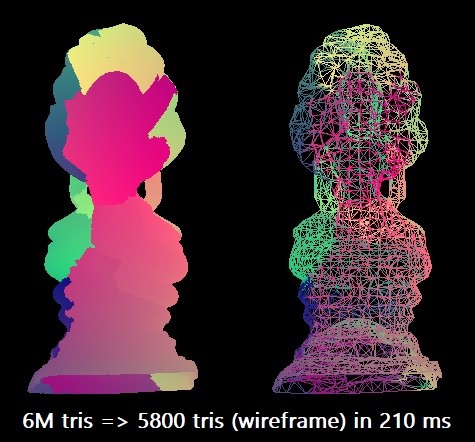
Untuk patokan kami, kami menyederhanakan model Buddha Thailand dari 6 juta segitiga menjadi 0,1% dari jumlah ini. Kami menggunakan kompiler Microsoft Visual Studio 2019 untuk arsitektur target x64. Algoritma skalar dapat melakukan rasionalisasi seperti itu di sekitar 210 ms dalam satu thread Intel Core i7-8700K (pada ~ 4,4 GHz). Ini sesuai dengan sekitar 28,5 juta segitiga per detik. Mungkin ini sudah cukup dalam praktiknya, tetapi saya penasaran ingin mengeksplorasi kemampuan maksimal dari peralatan tersebut.

Dalam beberapa kasus, prosedur dapat diparalelkan dengan membagi kisi-kisi menjadi potongan-potongan, tetapi untuk ini perlu melakukan analisis konektivitas tambahan untuk menjaga batas-batas, jadi untuk saat ini kami akan membatasi diri kami hanya untuk optimasi SIMD murni.

Tujuh pengukuran

Untuk memahami kemungkinan pengoptimalan, kami akan melakukan pembuatan profil menggunakan Intel VTune. Jalankan prosedur 100 kali untuk memastikan bahwa ada cukup data.



Di sini saya mengaktifkan mode mikroarsitektur untuk memperbaiki waktu eksekusi setiap fungsi, serta untuk menemukan kemacetan. Kita melihat bahwa rasionalisasi dilakukan dengan menggunakan serangkaian fungsi, yang masing-masing memerlukan sejumlah siklus. Daftar fungsi diurutkan berdasarkan waktu. Di sini mereka berada dalam urutan eksekusi untuk membuat algoritma lebih mudah dimengerti:

• rescalePositions menormalkan posisi semua simpul menjadi satu kubus untuk mempersiapkan kuantisasi menggunakan computeVertexIds
• computeVertexIds menghitung pengidentifikasi terkuantisasi 30-bit untuk setiap simpul pada kisi yang seragam dengan ukuran tertentu, di mana setiap sumbu dikuantisasi pada kisi (ukuran kisi 10 bit, jadi pengenalnya 30)
• countTriangles menghitung perkiraan jumlah segitiga yang akan dibuat oleh inovator untuk ukuran kisi tertentu, dengan asumsi penyatuan semua simpul dalam satu sel kisi
• fillVertexCells mengisi tabel yang fillVertexCells semua simpul ke sel yang sesuai; semua simpul dengan ID yang sama sesuai dengan satu sel
• fillCellQuadrics mengisi struktur Quadric ( Quadric symmetric matrix) untuk setiap sel untuk mencerminkan informasi agregat tentang geometri yang sesuai
• fillCellRemap menghitung indeks titik untuk setiap sel, memilih salah satu dari simpul dalam sel ini, dan meminimalkan distorsi geometrik
• filterTriangles menampilkan set terakhir segitiga sesuai dengan tabel vertex-sel-vertex yang dibangun sebelumnya; terjemahan naif dapat menghasilkan rata-rata ~ 5% duplikat segitiga, sehingga fungsinya memfilter duplikat.

computeVertexIds dan countTriangles dieksekusi beberapa kali: algoritma menentukan ukuran mesh untuk menggabungkan simpul, melakukan pencarian biner yang dipercepat untuk mencapai jumlah target segitiga (dalam kasus kami 6000) dan menghitung jumlah segitiga yang setiap ukuran mesh akan hasilkan pada setiap iterasi. Fungsi lain diluncurkan sekali. Dalam file kami, lima lintasan pencarian memberikan ukuran target mesh 40 ³ .

VTune sangat membantu melaporkan bahwa fungsi yang paling intensif sumber daya adalah fungsi yang menghitung kuadrik: dibutuhkan hampir setengah dari total waktu eksekusi 21 detik. Ini adalah tujuan pertama untuk mengoptimalkan SIMD.

SIMD sepotong demi sepotong

Mari kita lihat kode sumber fillCellQuadrics untuk lebih memahami apa yang sebenarnya dihitung:

 static void fillCellQuadrics(Quadric* cell_quadrics, const unsigned int* indices, size_t index_count, const Vector3* vertex_positions, const unsigned int* vertex_cells) { for (size_t i = 0; i < index_count; i += 3) { unsigned int i0 = indices[i + 0]; unsigned int i1 = indices[i + 1]; unsigned int i2 = indices[i + 2]; unsigned int c0 = vertex_cells[i0]; unsigned int c1 = vertex_cells[i1]; unsigned int c2 = vertex_cells[i2]; bool single_cell = (c0 == c1) & (c0 == c2); float weight = single_cell ? 3.f : 1.f; Quadric Q; quadricFromTriangle(Q, vertex_positions[i0], vertex_positions[i1], vertex_positions[i2], weight); if (single_cell) { quadricAdd(cell_quadrics[c0], Q); } else { quadricAdd(cell_quadrics[c0], Q); quadricAdd(cell_quadrics[c1], Q); quadricAdd(cell_quadrics[c2], Q); } } } 

Fungsi iterates atas semua segitiga, menghitung kuadrat untuk masing-masing, dan menambahkannya ke kuadrik setiap sel. Quadric - sebuah matriks simetris 4 × 4, disajikan sebagai 10 angka floating-point:

 struct Quadric { float a00; float a10, a11; float a20, a21, a22; float b0, b1, b2, c; }; 

Perhitungan quadric membutuhkan penyelesaian persamaan bidang untuk segitiga, membangun matriks kuadratik dan menimbangnya menggunakan luas segitiga:

 static void quadricFromPlane(Quadric& Q, float a, float b, float c, float d) { Q.a00 = a * a; Q.a10 = b * a; Q.a11 = b * b; Q.a20 = c * a; Q.a21 = c * b; Q.a22 = c * c; Q.b0 = d * a; Q.b1 = d * b; Q.b2 = d * c; Qc = d * d; } static void quadricFromTriangle(Quadric& Q, const Vector3& p0, const Vector3& p1, const Vector3& p2, float weight) { Vector3 p10 = {p1.x - p0.x, p1.y - p0.y, p1.z - p0.z}; Vector3 p20 = {p2.x - p0.x, p2.y - p0.y, p2.z - p0.z}; Vector3 normal = { p10.y * p20.z - p10.z * p20.y, p10.z * p20.x - p10.x * p20.z, p10.x * p20.y - p10.y * p20.x }; float area = normalize(normal); float distance = normal.x*p0.x + normal.y*p0.y + normal.z*p0.z; quadricFromPlane(Q, normal.x, normal.y, normal.z, -distance); quadricMul(Q, area * weight); } 

Sepertinya ada banyak operasi floating point, sehingga dapat diparalelkan menggunakan SIMD. Pertama, kami merepresentasikan setiap vektor sebagai vektor SIMD 4-lebar, dan juga mengubah struktur Quadric menjadi 12 angka floating point alih-alih 10 sehingga sesuai dengan tiga register SIMD (menambah ukuran tidak memengaruhi kinerja) dan mengubah urutan bidang sehingga perhitungan quadricFromPlane menjadi lebih seragam:

 struct Quadric { float a00, a11, a22; float pad0; float a10, a21, a20; float pad1; float b0, b1, b2, c; }; 

Di sini, beberapa perhitungan, khususnya produk skalar, tidak terlalu konsisten dengan versi SSE sebelumnya. Untungnya, instruksi untuk produk skalar muncul di SSE4.1, yang sangat berguna bagi kami.

 static void fillCellQuadrics(Quadric* cell_quadrics, const unsigned int* indices, size_t index_count, const Vector3* vertex_positions, const unsigned int* vertex_cells) { const int yzx = _MM_SHUFFLE(3, 0, 2, 1); const int zxy = _MM_SHUFFLE(3, 1, 0, 2); const int dp_xyz = 0x7f; for (size_t i = 0; i < index_count; i += 3) { unsigned int i0 = indices[i + 0]; unsigned int i1 = indices[i + 1]; unsigned int i2 = indices[i + 2]; unsigned int c0 = vertex_cells[i0]; unsigned int c1 = vertex_cells[i1]; unsigned int c2 = vertex_cells[i2]; bool single_cell = (c0 == c1) & (c0 == c2); __m128 p0 = _mm_loadu_ps(&vertex_positions[i0].x); __m128 p1 = _mm_loadu_ps(&vertex_positions[i1].x); __m128 p2 = _mm_loadu_ps(&vertex_positions[i2].x); __m128 p10 = _mm_sub_ps(p1, p0); __m128 p20 = _mm_sub_ps(p2, p0); __m128 normal = _mm_sub_ps( _mm_mul_ps( _mm_shuffle_ps(p10, p10, yzx), _mm_shuffle_ps(p20, p20, zxy)), _mm_mul_ps( _mm_shuffle_ps(p10, p10, zxy), _mm_shuffle_ps(p20, p20, yzx))); __m128 areasq = _mm_dp_ps(normal, normal, dp_xyz); // SSE4.1 __m128 area = _mm_sqrt_ps(areasq); // masks the result of the division when area==0 // scalar version does this in normalize() normal = _mm_and_ps( _mm_div_ps(normal, area), _mm_cmpneq_ps(area, _mm_setzero_ps())); __m128 distance = _mm_dp_ps(normal, p0, dp_xyz); // SSE4.1 __m128 negdistance = _mm_sub_ps(_mm_setzero_ps(), distance); __m128 normalnegdist = _mm_blend_ps(normal, negdistance, 8); __m128 Qx = _mm_mul_ps(normal, normal); __m128 Qy = _mm_mul_ps( _mm_shuffle_ps(normal, normal, _MM_SHUFFLE(3, 2, 2, 1)), _mm_shuffle_ps(normal, normal, _MM_SHUFFLE(3, 0, 1, 0))); __m128 Qz = _mm_mul_ps(negdistance, normalnegdist); if (single_cell) { area = _mm_mul_ps(area, _mm_set1_ps(3.f)); Qx = _mm_mul_ps(Qx, area); Qy = _mm_mul_ps(Qy, area); Qz = _mm_mul_ps(Qz, area); Quadric& q0 = cell_quadrics[c0]; __m128 q0x = _mm_loadu_ps(&q0.a00); __m128 q0y = _mm_loadu_ps(&q0.a10); __m128 q0z = _mm_loadu_ps(&q0.b0); _mm_storeu_ps(&q0.a00, _mm_add_ps(q0x, Qx)); _mm_storeu_ps(&q0.a10, _mm_add_ps(q0y, Qy)); _mm_storeu_ps(&q0.b0, _mm_add_ps(q0z, Qz)); } else { // omitted for brevity, repeats the if() body // three times for c0/c1/c2 } } } 

Tidak ada yang menarik dalam kode ini; kami banyak menggunakan instruksi pemuatan / penyimpanan yang tidak selaras. Meskipun input Vector3 dapat disejajarkan, tampaknya tidak ada penalti yang nyata untuk pembacaan yang tidak selaras. Harap dicatat bahwa pada paruh pertama vektor fungsi tidak digunakan, yang bagus - vektor kami memiliki tiga komponen, dan dalam beberapa kasus hanya satu (lihat perhitungan q area / area / jarak), sementara prosesor melakukan 4 operasi secara paralel. Bagaimanapun, mari kita lihat bagaimana paralelisasi telah membantu.



Seratus mulai dari fillCellQuadrics sekarang berjalan dalam 5,3 detik, bukan 9,8 detik, yang menghemat sekitar 45 ms pada setiap operasi - tidak buruk, tetapi tidak terlalu mengesankan. Dalam banyak instruksi, kami menggunakan tiga bukannya empat komponen, serta perkalian yang tepat, yang memberikan penundaan yang cukup signifikan. Jika sebelumnya Anda menulis instruksi untuk SIMD, maka Anda tahu bagaimana melakukan produk skalar dengan benar.

Untuk melakukan ini, Anda perlu melakukan empat vektor sekaligus. Alih-alih menyimpan satu vektor lengkap dalam satu register SIMD, kami menggunakan tiga register - dalam satu kami menyimpan empat komponen x , yang lain kami akan menyimpan , dan di z ketiga. Di sini empat vektor diperlukan untuk bekerja sekaligus: itu artinya kita akan memproses empat segitiga secara bersamaan.

Kami memiliki banyak array dengan pengindeksan dinamis. Biasanya, ini membantu untuk mentransfer data ke array disiapkan komponen x / y / z (atau lebih tepatnya, register SIMD kecil biasanya digunakan, misalnya, float x[8], y[8], z[8] , untuk masing-masing dari 8 simpul dalam input data: ini disebut AoSoA (susunan susunan array) dan memberikan keseimbangan yang baik antara cache lokalitas dan kemudahan memuat ke register SIMD), tetapi di sini pengindeksan dinamis tidak akan bekerja dengan baik, jadi muatkan data untuk empat segitiga seperti biasa, dan transpos vektor menggunakan nyaman makro _MM_TRANSPOSE .

Secara teoritis, Anda perlu menghitung setiap komponen dari empat kuadrat terbatas dalam register SIMD-nya sendiri (misalnya, kita akan memiliki __m128 Q_a00 dengan empat komponen a00 terbatas a00 ). Dalam kasus ini, operasi pada kuadrik cukup sesuai dengan instruksi SIMD 4-lebar, dan konversi sebenarnya memperlambat kode - oleh karena itu, kami hanya mentransposisikan vektor awal, dan kemudian memindahkan persamaan pesawat kembali dan menjalankan kode yang sama yang kami gunakan untuk menghitung kuadrik, tetapi ulangi empat kali. Berikut adalah kode yang kemudian menghitung persamaan bidang (bagian-bagian lainnya dihilangkan untuk singkatnya):

 unsigned int i00 = indices[(i + 0) * 3 + 0]; unsigned int i01 = indices[(i + 0) * 3 + 1]; unsigned int i02 = indices[(i + 0) * 3 + 2]; unsigned int i10 = indices[(i + 1) * 3 + 0]; unsigned int i11 = indices[(i + 1) * 3 + 1]; unsigned int i12 = indices[(i + 1) * 3 + 2]; unsigned int i20 = indices[(i + 2) * 3 + 0]; unsigned int i21 = indices[(i + 2) * 3 + 1]; unsigned int i22 = indices[(i + 2) * 3 + 2]; unsigned int i30 = indices[(i + 3) * 3 + 0]; unsigned int i31 = indices[(i + 3) * 3 + 1]; unsigned int i32 = indices[(i + 3) * 3 + 2]; // load first vertex of each triangle and transpose into vectors with components (pw0 isn't used later) __m128 px0 = _mm_loadu_ps(&vertex_positions[i00].x); __m128 py0 = _mm_loadu_ps(&vertex_positions[i10].x); __m128 pz0 = _mm_loadu_ps(&vertex_positions[i20].x); __m128 pw0 = _mm_loadu_ps(&vertex_positions[i30].x); _MM_TRANSPOSE4_PS(px0, py0, pz0, pw0); // load second vertex of each triangle and transpose into vectors with components __m128 px1 = _mm_loadu_ps(&vertex_positions[i01].x); __m128 py1 = _mm_loadu_ps(&vertex_positions[i11].x); __m128 pz1 = _mm_loadu_ps(&vertex_positions[i21].x); __m128 pw1 = _mm_loadu_ps(&vertex_positions[i31].x); _MM_TRANSPOSE4_PS(px1, py1, pz1, pw1); // load third vertex of each triangle and transpose into vectors with components __m128 px2 = _mm_loadu_ps(&vertex_positions[i02].x); __m128 py2 = _mm_loadu_ps(&vertex_positions[i12].x); __m128 pz2 = _mm_loadu_ps(&vertex_positions[i22].x); __m128 pw2 = _mm_loadu_ps(&vertex_positions[i32].x); _MM_TRANSPOSE4_PS(px2, py2, pz2, pw2); // p1 - p0 __m128 px10 = _mm_sub_ps(px1, px0); __m128 py10 = _mm_sub_ps(py1, py0); __m128 pz10 = _mm_sub_ps(pz1, pz0); // p2 - p0 __m128 px20 = _mm_sub_ps(px2, px0); __m128 py20 = _mm_sub_ps(py2, py0); __m128 pz20 = _mm_sub_ps(pz2, pz0); // cross(p10, p20) __m128 normalx = _mm_sub_ps( _mm_mul_ps(py10, pz20), _mm_mul_ps(pz10, py20)); __m128 normaly = _mm_sub_ps( _mm_mul_ps(pz10, px20), _mm_mul_ps(px10, pz20)); __m128 normalz = _mm_sub_ps( _mm_mul_ps(px10, py20), _mm_mul_ps(py10, px20)); // normalize; note that areasq/area now contain 4 values, not just one __m128 areasq = _mm_add_ps( _mm_mul_ps(normalx, normalx), _mm_add_ps( _mm_mul_ps(normaly, normaly), _mm_mul_ps(normalz, normalz))); __m128 area = _mm_sqrt_ps(areasq); __m128 areanz = _mm_cmpneq_ps(area, _mm_setzero_ps()); normalx = _mm_and_ps(_mm_div_ps(normalx, area), areanz); normaly = _mm_and_ps(_mm_div_ps(normaly, area), areanz); normalz = _mm_and_ps(_mm_div_ps(normalz, area), areanz); __m128 distance = _mm_add_ps( _mm_mul_ps(normalx, px0), _mm_add_ps( _mm_mul_ps(normaly, py0), _mm_mul_ps(normalz, pz0))); __m128 negdistance = _mm_sub_ps(_mm_setzero_ps(), distance); // this computes the plane equations (a, b, c, d) for each of the 4 triangles __m128 plane0 = normalx; __m128 plane1 = normaly; __m128 plane2 = normalz; __m128 plane3 = negdistance; _MM_TRANSPOSE4_PS(plane0, plane1, plane2, plane3); 

Kode telah menjadi sedikit lebih lama: sekarang kami memproses empat segitiga di setiap iterasi, dan kami tidak lagi memerlukan instruksi SSE4.1 untuk ini. Secara teori, unit SIMD harus digunakan lebih efisien. Mari kita lihat bagaimana ini membantu.



Oke, tidak apa-apa. Kode telah dipercepat sangat sedikit, meskipun fungsi fillCellQuadrics sekarang berjalan hampir dua kali lebih cepat dari fungsi asli tanpa SIMD, tetapi tidak jelas apakah ini membenarkan peningkatan kompleksitas yang signifikan. Secara teoritis, Anda dapat menggunakan AVX2 dan memproses 8 segitiga per iterasi, tetapi di sini Anda perlu memutar lebih lanjut loop secara manual (idealnya, semua kode ini dihasilkan menggunakan ISPC, tetapi upaya naif saya untuk mendapatkannya menghasilkan kode yang baik tidak berhasil: alih-alih urutan beban / store bukan ia terus-menerus mengeluarkan pengumpulan / pencar, yang secara signifikan memperlambat eksekusi). Mari kita coba yang lain.

AVX2 = SSE2 + SSE2

AVX2 adalah sekumpulan instruksi. Ini memiliki register floating point selebar 8, dan satu instruksi dapat melakukan 8 operasi; tetapi pada kenyataannya, instruksi semacam itu tidak berbeda dari dua instruksi SSE2 yang dieksekusi pada dua bagian register (sejauh yang saya mengerti, prosesor pertama dengan dukungan AVX2 mendekodekan setiap instruksi dalam dua atau lebih operasi mikro, oleh karena itu peningkatan kinerja dibatasi oleh fase instruksi penggalian). Sebagai contoh, _mm_dp_ps melakukan produk skalar antara dua register SSE2, dan _mm256_dp_ps menghasilkan dua produk skalar antara dua bagian dari dua register AVX2, oleh karena itu dibatasi hingga 4-lebar untuk setiap setengahnya.

Karena itu, kode AVX2 sering berbeda dari “8-wide SIMD” universal, tetapi di sini ia bekerja sesuai keinginan kami: alih-alih mencoba meningkatkan vektorisasi dengan mentransposisi vektor 4-lebar, kami kembali ke versi pertama SIMD dan menggandakan loop menggunakan instruksi AVX2 alih-alih SSE2 / SSE4. Kita masih perlu memuat dan menyimpan vektor 4-lebar, tetapi secara umum, kita hanya mengubah __m128 menjadi __m256 dan _mm_ menjadi _mm256 dalam _mm256 dengan beberapa pengaturan:

 unsigned int i00 = indices[(i + 0) * 3 + 0]; unsigned int i01 = indices[(i + 0) * 3 + 1]; unsigned int i02 = indices[(i + 0) * 3 + 2]; unsigned int i10 = indices[(i + 1) * 3 + 0]; unsigned int i11 = indices[(i + 1) * 3 + 1]; unsigned int i12 = indices[(i + 1) * 3 + 2]; __m256 p0 = _mm256_loadu2_m128( &vertex_positions[i10].x, &vertex_positions[i00].x); __m256 p1 = _mm256_loadu2_m128( &vertex_positions[i11].x, &vertex_positions[i01].x); __m256 p2 = _mm256_loadu2_m128( &vertex_positions[i12].x, &vertex_positions[i02].x); __m256 p10 = _mm256_sub_ps(p1, p0); __m256 p20 = _mm256_sub_ps(p2, p0); __m256 normal = _mm256_sub_ps( _mm256_mul_ps( _mm256_shuffle_ps(p10, p10, yzx), _mm256_shuffle_ps(p20, p20, zxy)), _mm256_mul_ps( _mm256_shuffle_ps(p10, p10, zxy), _mm256_shuffle_ps(p20, p20, yzx))); __m256 areasq = _mm256_dp_ps(normal, normal, dp_xyz); __m256 area = _mm256_sqrt_ps(areasq); __m256 areanz = _mm256_cmp_ps(area, _mm256_setzero_ps(), _CMP_NEQ_OQ); normal = _mm256_and_ps(_mm256_div_ps(normal, area), areanz); __m256 distance = _mm256_dp_ps(normal, p0, dp_xyz); __m256 negdistance = _mm256_sub_ps(_mm256_setzero_ps(), distance); __m256 normalnegdist = _mm256_blend_ps(normal, negdistance, 0x88); __m256 Qx = _mm256_mul_ps(normal, normal); __m256 Qy = _mm256_mul_ps( _mm256_shuffle_ps(normal, normal, _MM_SHUFFLE(3, 2, 2, 1)), _mm256_shuffle_ps(normal, normal, _MM_SHUFFLE(3, 0, 1, 0))); __m256 Qz = _mm256_mul_ps(negdistance, normalnegdist); 

Di sini Anda dapat mengambil setiap 128-bit setengah dari Qz Qx / Qz / Qz diterima dan menjalankan kode yang sama yang kami gunakan untuk menambahkan kuadrik. Sebaliknya, kami mengasumsikan bahwa jika segitiga memiliki tiga simpul dalam satu sel ( single_cell == true ), maka sangat mungkin bahwa segitiga lain memiliki tiga simpul di sel lain, dan kami melakukan agregasi akhir kuadrat menggunakan AVX2 juga:

 unsigned int c00 = vertex_cells[i00]; unsigned int c01 = vertex_cells[i01]; unsigned int c02 = vertex_cells[i02]; unsigned int c10 = vertex_cells[i10]; unsigned int c11 = vertex_cells[i11]; unsigned int c12 = vertex_cells[i12]; bool single_cell = (c00 == c01) & (c00 == c02) & (c10 == c11) & (c10 == c12); if (single_cell) { area = _mm256_mul_ps(area, _mm256_set1_ps(3.f)); Qx = _mm256_mul_ps(Qx, area); Qy = _mm256_mul_ps(Qy, area); Qz = _mm256_mul_ps(Qz, area); Quadric& q00 = cell_quadrics[c00]; Quadric& q10 = cell_quadrics[c10]; __m256 q0x = _mm256_loadu2_m128(&q10.a00, &q00.a00); __m256 q0y = _mm256_loadu2_m128(&q10.a10, &q00.a10); __m256 q0z = _mm256_loadu2_m128(&q10.b0, &q00.b0); _mm256_storeu2_m128(&q10.a00, &q00.a00, _mm256_add_ps(q0x, Qx)); _mm256_storeu2_m128(&q10.a10, &q00.a10, _mm256_add_ps(q0y, Qy)); _mm256_storeu2_m128(&q10.b0, &q00.b0, _mm256_add_ps(q0z, Qz)); } else { // omitted for brevity } 

Kode yang dihasilkan lebih sederhana, ringkas, dan lebih cepat daripada pendekatan SSE2 kami yang gagal:



Tentu saja, kami tidak mencapai akselerasi 8 kali, tetapi hanya 2,45 kali. Pengoperasian load dan store masih 4-lebar, karena kami dipaksa untuk bekerja dengan tata letak memori yang tidak nyaman karena pengindeksan dinamis, dan perhitungannya tidak optimal untuk SIMD. Tetapi sekarang fillCellQuadrics tidak lagi menjadi hambatan dalam pipa profil kami, dan Anda dapat fokus pada fungsi-fungsi lain.

Berkumpul, anak-anak

Kami menghemat 4,8 detik pada uji coba (48 ms pada setiap uji coba), dan sekarang penyusup utama kami adalah countTriangles . Tampaknya ini adalah fungsi sederhana, tetapi dijalankan bukan hanya sekali, tetapi lima kali:

 static size_t countTriangles(const unsigned int* vertex_ids, const unsigned int* indices, size_t index_count) { size_t result = 0; for (size_t i = 0; i < index_count; i += 3) { unsigned int id0 = vertex_ids[indices[i + 0]]; unsigned int id1 = vertex_ids[indices[i + 1]]; unsigned int id2 = vertex_ids[indices[i + 2]]; result += (id0 != id1) & (id0 != id2) & (id1 != id2); } return result; } 

Fungsi ini mengulangi semua segitiga sumber dan menghitung jumlah segitiga non-degenerasi dengan membandingkan pengidentifikasi simpul. Tidak segera jelas cara memparalelkannya menggunakan SIMD ... kecuali jika Anda menggunakan instruksi kumpulkan.

Set instruksi AVX2 menambahkan kumpulan instruksi assemb / scatter ke x64 SIMD; masing-masing dari mereka mengambil register vektor dengan 4 atau 8 nilai - dan secara bersamaan melakukan 4 atau 8 memuat atau menyimpan operasi. Jika Anda menggunakan kumpulkan di sini, Anda dapat mengunduh tiga indeks, menjalankan kumpul untuk semuanya sekaligus (atau dalam kelompok 4 atau 8) dan membandingkan hasilnya. Kumpulkan pada prosesor Intel secara historis sangat lambat, tapi mari kita coba. Untuk kesederhanaan, kami mengunggah data untuk 8 segitiga, memindahkan vektor dengan cara yang sama dengan upaya kami sebelumnya, dan membandingkan elemen terkait dari setiap vektor:

 for (size_t i = 0; i < (triangle_count & ~7); i += 8) { __m256 tri0 = _mm256_loadu2_m128( (const float*)&indices[(i + 4) * 3 + 0], (const float*)&indices[(i + 0) * 3 + 0]); __m256 tri1 = _mm256_loadu2_m128( (const float*)&indices[(i + 5) * 3 + 0], (const float*)&indices[(i + 1) * 3 + 0]); __m256 tri2 = _mm256_loadu2_m128( (const float*)&indices[(i + 6) * 3 + 0], (const float*)&indices[(i + 2) * 3 + 0]); __m256 tri3 = _mm256_loadu2_m128( (const float*)&indices[(i + 7) * 3 + 0], (const float*)&indices[(i + 3) * 3 + 0]); _MM_TRANSPOSE8_LANE4_PS(tri0, tri1, tri2, tri3); __m256i i0 = _mm256_castps_si256(tri0); __m256i i1 = _mm256_castps_si256(tri1); __m256i i2 = _mm256_castps_si256(tri2); __m256i id0 = _mm256_i32gather_epi32((int*)vertex_ids, i0, 4); __m256i id1 = _mm256_i32gather_epi32((int*)vertex_ids, i1, 4); __m256i id2 = _mm256_i32gather_epi32((int*)vertex_ids, i2, 4); __m256i deg = _mm256_or_si256( _mm256_cmpeq_epi32(id1, id2), _mm256_or_si256( _mm256_cmpeq_epi32(id0, id1), _mm256_cmpeq_epi32(id0, id2))); result += 8 - _mm_popcnt_u32(_mm256_movemask_epi8(deg)) / 4; } 

Makro _MM_TRANSPOSE8_LANE4_PS di AVX2 adalah setara dengan _MM_TRANSPOSE4_PS , yang tidak ditemukan di tajuk standar, tetapi mudah ditampilkan. Dibutuhkan empat vektor AVX2 dan transpos dua matriks 4 × 4 secara independen satu sama lain:

 #define _MM_TRANSPOSE8_LANE4_PS(row0, row1, row2, row3) \ do { \ __m256 __t0, __t1, __t2, __t3; \ __t0 = _mm256_unpacklo_ps(row0, row1); \ __t1 = _mm256_unpackhi_ps(row0, row1); \ __t2 = _mm256_unpacklo_ps(row2, row3); \ __t3 = _mm256_unpackhi_ps(row2, row3); \ row0 = _mm256_shuffle_ps(__t0, __t2, _MM_SHUFFLE(1, 0, 1, 0)); \ row1 = _mm256_shuffle_ps(__t0, __t2, _MM_SHUFFLE(3, 2, 3, 2)); \ row2 = _mm256_shuffle_ps(__t1, __t3, _MM_SHUFFLE(1, 0, 1, 0)); \ row3 = _mm256_shuffle_ps(__t1, __t3, _MM_SHUFFLE(3, 2, 3, 2)); \ } while (0) 

Karena beberapa fitur dalam set instruksi SSE2 / AVX2, kita harus menggunakan operasi register titik mengambang ketika mentransposisi vektor. Kami memuat data sedikit sembarangan; tetapi pada dasarnya tidak masalah, karena mengumpulkan kinerja membatasi kita:



Sekarang countTriangles sekitar 27% lebih cepat dan memperhatikan CPI yang mengerikan (siklus per instruksi): kami mengirimkan sekitar empat kali lebih sedikit instruksi, tetapi mengumpulkan membutuhkan banyak waktu. Sangat bagus karena mempercepat pekerjaan secara keseluruhan, tetapi, tentu saja, peningkatan kinerja agak menyedihkan. Kami berhasil menyalip fillCellQuadrics di profil, yang membawa kami ke fungsi terakhir di bagian atas daftar yang belum kami lihat.

Bab 6, di mana semuanya mulai bekerja sebagaimana mestinya

Fungsi terakhir adalah computeVertexIds . Dalam algoritma, ini dilakukan 6 kali, oleh karena itu juga merupakan tujuan yang sangat baik untuk optimasi. Untuk pertama kalinya, kami melihat fungsi yang tampaknya dibuat untuk optimisasi yang jelas di SIMD:

 static void computeVertexIds(unsigned int* vertex_ids, const Vector3* vertex_positions, size_t vertex_count, int grid_size) { assert(grid_size >= 1 && grid_size <= 1024); float cell_scale = float(grid_size - 1); for (size_t i = 0; i < vertex_count; ++i) { const Vector3& v = vertex_positions[i]; int xi = int(vx * cell_scale + 0.5f); int yi = int(vy * cell_scale + 0.5f); int zi = int(vz * cell_scale + 0.5f); vertex_ids[i] = (xi << 20) | (yi << 10) | zi; } } 

Setelah optimasi sebelumnya, kita tahu apa yang harus dilakukan: melepas siklus 4 atau 8 kali, karena tidak ada gunanya mencoba mempercepat hanya satu iterasi, transpos komponen vektor dan jalankan perhitungan secara paralel. Mari kita lakukan dengan AVX2, memproses 8 simpul sekaligus:

 __m256 scale = _mm256_set1_ps(cell_scale); __m256 half = _mm256_set1_ps(0.5f); for (size_t i = 0; i < (vertex_count & ~7); i += 8) { __m256 vx = _mm256_loadu2_m128( &vertex_positions[i + 4].x, &vertex_positions[i + 0].x); __m256 vy = _mm256_loadu2_m128( &vertex_positions[i + 5].x, &vertex_positions[i + 1].x); __m256 vz = _mm256_loadu2_m128( &vertex_positions[i + 6].x, &vertex_positions[i + 2].x); __m256 vw = _mm256_loadu2_m128( &vertex_positions[i + 7].x, &vertex_positions[i + 3].x); _MM_TRANSPOSE8_LANE4_PS(vx, vy, vz, vw); __m256i xi = _mm256_cvttps_epi32( _mm256_add_ps(_mm256_mul_ps(vx, scale), half)); __m256i yi = _mm256_cvttps_epi32( _mm256_add_ps(_mm256_mul_ps(vy, scale), half)); __m256i zi = _mm256_cvttps_epi32( _mm256_add_ps(_mm256_mul_ps(vz, scale), half)); __m256i id = _mm256_or_si256( zi, _mm256_or_si256( _mm256_slli_epi32(xi, 20), _mm256_slli_epi32(yi, 10))); _mm256_storeu_si256((__m256i*)&vertex_ids[i], id); } 

Dan lihat hasilnya:



Kami mempercepat computeVertexIdsdua kali. Dengan mempertimbangkan semua optimasi, total waktu pelaksanaan program dikurangi menjadi sekitar 120 ms, yang sesuai dengan perhitungan 50 juta segitiga per detik.

Tampaknya kita sekali lagi tidak mencapai peningkatan yang diharapkan dalam produktivitas: computeVertexIdsbukankah harus mempercepat lebih dari dua kali setelah paralelisasi? Untuk menjawab pertanyaan ini, mari kita coba untuk melihat seberapa banyak kerja fungsi ini dilakukan.

computeVertexIdsitu dieksekusi enam kali untuk satu program mulai: lima kali selama pencarian biner dan sekali pada akhir untuk menghitung pengidentifikasi akhir yang digunakan untuk diproses lebih lanjut. Setiap kali, fungsi ini memproses 3 juta simpul, membaca 12 byte untuk setiap simpul dan menulis 4 byte.

Secara total, lebih dari 100 berjalan inovator, fungsi ini memproses 1,8 miliar simpul, membaca 21 GB dan menulis kembali 7 GB. Memproses 28 GB dalam 1,46 detik membutuhkan bandwidth bus 19 GB / s. Kami dapat memeriksa bandwidth memori dengan menjalankan memcmp(block1, block2, 512 MB). Hasilnya adalah 45 ms, yaitu sekitar 22 GB / s pada satu inti (meskipun tolok ukur AIDA64 menunjukkan kecepatan baca di sistem saya hingga 31 GB / s, tetapi menggunakan beberapa core). Faktanya, kita telah mendekati batas memori maksimum yang dapat dicapai, dan peningkatan kinerja lebih lanjut akan membutuhkan pengemasan yang lebih dekat dari simpul-simpul ini sehingga mereka menempati kurang dari 12 byte.

Kesimpulan

Kami mengambil algoritma yang dioptimalkan dengan cukup baik yang menyederhanakan kisi-kisi yang sangat besar dengan kecepatan 28 juta segitiga per detik, dan menggunakan set instruksi SSE dan AVX untuk mempercepatnya hampir dua kali lipat, hingga 50 juta segitiga per detik. Selama perjalanan ini, kami harus belajar berbagai cara untuk menggunakan SIMD: register untuk menyimpan vektor 3-lebar, SoA transpose, instruksi AVX2 untuk menyimpan dua vektor 3-lebar, mengumpulkan instruksi untuk mempercepat pemuatan data dibandingkan dengan instruksi skalar, dan akhirnya kami langsung menerapkan AVX2 untuk pemrosesan streaming.

SIMD sering bukan titik awal terbaik untuk optimasi: rasionalisasi mesh melewati banyak iterasi optimasi algoritmik dan optimasi mikro tanpa menggunakan instruksi platform spesifik. Tetapi pada titik tertentu, kemungkinan ini habis, dan jika kinerja sangat penting, maka SIMD adalah alat yang fantastis yang dapat digunakan jika perlu.

Saya tidak yakin yang mana dari optimasi ini akan jatuh ke cabang utama meshoptimizer: pada akhirnya, ini hanya sebuah percobaan untuk melihat bagaimana overclock kode tanpa mengubah secara drastis algoritma. Saya harap artikel ini ternyata informatif dan memberi Anda ide untuk mengoptimalkan kode. Sumber terakhir untuk artikel ini ada di sini ; pekerjaan ini didasarkan pada versi meshoptimizer 99ab49, dan model Buddha Thailand diterbitkan di Sketchfab .