Pendahuluan
Beberapa artikel [1,2,3] telah dipublikasikan di Habr yang secara langsung atau tidak langsung berkaitan dengan topik ini. Dalam hal ini, orang tidak dapat gagal untuk mencatat publikasi [1] dengan judul "Matematika pada Jari: Regulator Linier-Kuadratik", yang populer menjelaskan prinsip operasi pengontrol LQR optimal.
Saya ingin melanjutkan topik ini, setelah memeriksa aplikasi praktis dari metode optimasi dinamis, tetapi sudah pada contoh nyata menggunakan Python. Pertama, beberapa kata tentang terminologi dan metode optimasi dinamis.
Metode optimasi dibagi menjadi statis dan dinamis. Objek kontrol berada dalam keadaan gerakan terus menerus di bawah pengaruh berbagai faktor eksternal dan internal. Oleh karena itu, evaluasi hasil kontrol diberikan untuk waktu kontrol T, dan ini adalah tugas optimasi dinamis.
Menggunakan metode optimisasi dinamis, masalah yang terkait dengan distribusi sumber daya terbatas selama periode waktu tertentu diselesaikan, dan fungsi tujuan ditulis sebagai fungsional integral.
Alat matematika untuk memecahkan masalah tersebut adalah metode variasional: kalkulus variasi klasik, prinsip L.S. maksimum. Pontryagin dan pemrograman dinamis R. Bellman.
Analisis dan sintesis sistem kontrol dilakukan dalam ruang waktu, frekuensi, dan keadaan. Analisis dan sintesis sistem kontrol di ruang negara dimasukkan ke dalam kurikulum, namun, teknik yang disajikan dalam materi pelatihan menggunakan pengontrol SQR dirancang untuk menggunakan Matlab dan tidak mengandung contoh praktis analisis.
Tujuan dari publikasi ini adalah untuk mempertimbangkan metode analisis dan sintesis sistem kontrol linier di ruang negara menggunakan contoh terkenal mengoptimalkan sistem kontrol drive listrik dan pesawat terbang menggunakan bahasa pemrograman Python.
Pembuktian matematis dari metode optimasi dinamis
Untuk optimasi, kriteria amplitudo (MO), simetris (CO) dan kompromi optimum (KO) digunakan.
Ketika memecahkan masalah optimisasi dalam ruang keadaan, sistem stasioner linier diberikan oleh persamaan vektor-matriks:
dotx= fracdxdt=A cdotx+B cdotu;y=C cdotx, (1)
Kriteria integral untuk konsumsi energi kontrol minimum dan kecepatan maksimum ditetapkan oleh fungsi:
Jx= int infty0(xTQx+uTRu+2xTNu)dt rightarrowmin, (2)
Ju= int infty0(yTQy+uTRu+2yTNu)dt rightarrowmin. (3)
Hukum kontrol u adalah dalam bentuk umpan balik linier pada variabel status x atau pada variabel output y:
u= pmKx,u= pmKyKontrol tersebut meminimalkan kriteria kualitas kuadrat (2), (3). Dalam hubungan (1) ÷ (3), Q dan R adalah matriks pasti definitif positif simetris dari dimensi [n × n] dan [m × m], masing-masing; K adalah matriks koefisien konstan dimensi [m × n], yang nilainya tidak terbatas. Jika parameter input N dihilangkan, ini diambil menjadi nol.
Solusi untuk masalah ini, yang disebut masalah linear integral kuadrat optimasi (LQR-optimasi), dalam ruang keadaan ditentukan oleh ekspresi:
u=R−1BTPxdi mana matriks P harus memenuhi persamaan Ricatti:
ATP+PA+PBR−1BTP+Q=0Kriteria (2), (3) juga bertentangan, karena penerapan istilah pertama membutuhkan sumber daya yang sangat tinggi, dan untuk yang kedua, sumber daya yang sangat rendah. Ini dapat dijelaskan dengan ungkapan berikut:
Jx= int infty0xTQxdt ,
yang merupakan norma
Mod(x) vektor x, mis. ukuran osilasi dalam proses regulasi, dan, oleh karena itu, mengambil nilai yang lebih kecil dalam transien cepat dengan osilasi lebih sedikit, dan ungkapan:
Ju= int infty0uTRudtadalah ukuran dari jumlah energi yang digunakan untuk kontrol, itu adalah penalti untuk biaya energi sistem.
Matriks bobot Q, R, dan N menentukan batasan koordinat yang sesuai. Jika ada elemen dari matriks ini sama dengan nol, maka koordinat yang sesuai tidak memiliki batasan. Dalam praktiknya, pemilihan nilai matriks Q, R, N dilakukan dengan metode estimasi ahli, uji coba, kesalahan dan tergantung pada pengalaman dan pengetahuan insinyur desain.
Untuk mengatasi masalah tersebut, operator MATLAB berikut digunakan:
beginbmatrixR,S,E endbmatrix=lqr(A,B,Q,R,N) dan
beginbmatrixR,S,E endbmatrix=lqry(Ps,Q,R,N) yang meminimalkan fungsional (2), (3) oleh vektor negara x atau oleh vektor keluaran y.
Model Obyek Manajemen
Ps=ss(A,B,C,D). Hasil perhitungan adalah matriks K dari umpan balik optimal sehubungan dengan variabel keadaan x, solusi dari persamaan Ricatti S dan nilai eigen E = eiq (A-BK) dari sistem kontrol loop tertutup.
Komponen fungsional:
Jx=x0TP1x0,Ju=x0TP2x0di mana x0 adalah vektor kondisi awal;
P1 dan
P2 - Matriks yang tidak diketahui yang merupakan solusi dari persamaan matriks Lyapunov. Mereka ditemukan menggunakan fungsi;
P1=lyap(NN,Q) dan
P2=lyap(NN,KTRK) ,
NN=(A+BK)TFitur implementasi metode optimasi dinamis menggunakan Python
Meskipun Python Control Systems Library [4] memiliki fungsi: control.lqr, control.lyap, penggunaan control.lqr hanya dimungkinkan jika modul slycot diinstal, yang merupakan masalah [5]. Ketika menggunakan fungsi lyap dalam konteks tugas, hasil optimasi dalam control.exception.ControlArgument: Q harus menjadi kesalahan matriks simetris [6].
Oleh karena itu, untuk mengimplementasikan fungsi lqr () dan lyap (), saya menggunakan scipy.linalg:
from numpy import* from scipy.linalg import* def lqr(A,B,Q,R): S =matrix(solve_continuous_are(A, B, Q, R)) K = matrix(inv(R)*(BT*S)) E= eig(AB*K)[0] return K, S, E P1=solve_lyapunov(NN,Ct*Q*C)
Omong-omong, Anda seharusnya tidak sepenuhnya meninggalkan kontrol, karena fungsi step (), pole (), ss (), tf (), feedback (), acker (), place () dan lainnya berfungsi dengan baik.
Contoh optimasi LQR dalam drive listrik
(contoh diambil dari publikasi [7])Pertimbangkan sintesis pengontrol linear-kuadratik yang memenuhi kriteria (2) untuk objek kontrol yang didefinisikan dalam ruang keadaan oleh matriks:
A = \ begin {bmatrix} & -100 & 0 & 0 \\ & 143.678 & -16.667 & -195.402 \\ & 0 & 1.046 & 0 \ end {bmatrix}; B = \ begin {bmatrix} 2300 \\ 0 \\ 0 end {bmatrix}; C = \ begin {bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \ end {bmatrix}; D = 0
A = \ begin {bmatrix} & -100 & 0 & 0 \\ & 143.678 & -16.667 & -195.402 \\ & 0 & 1.046 & 0 \ end {bmatrix}; B = \ begin {bmatrix} 2300 \\ 0 \\ 0 end {bmatrix}; C = \ begin {bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \ end {bmatrix}; D = 0
Berikut ini dianggap sebagai variabel keadaan:
x1 - tegangan konverter, V;
x2 - Arus motor, A;
x3 - kecepatan sudut
c−1 . Ini adalah sistem TP-DPT dengan HB: engine R nom = 30 kW; Unom = 220 V; Inom = 147 A ;;
omegaω 0 = 169
c−1 ;
omegaω maks = 187
c−1 ; momen resistansi nominal Mnom = 150 N * m; banyaknya arus mulai = 2; thyristor converter: Unom = 230 V; Uy = 10 B; Inom = 300 A; multiplisitas arus lebih pendek = 1.2.
Saat memecahkan masalah, kami menerima matriks Q diagonal. Sebagai hasil pemodelan, ditemukan bahwa nilai minimum elemen matriks R = 84, dan
Q=[[0,01,0,0],[0,0,01,0],[0,0,0,01]]. Dalam hal ini, proses transisi monoton dari kecepatan sudut mesin diamati (Gbr. 1). Pada R = 840
Q=[[0,01,0,0],[0,0,01,0],[0,0,0,01]] proses transien (Gbr. 2) memenuhi kriteria MO. Perhitungan matriks P1 dan P2 dilakukan pada x0 = [220 147 162].
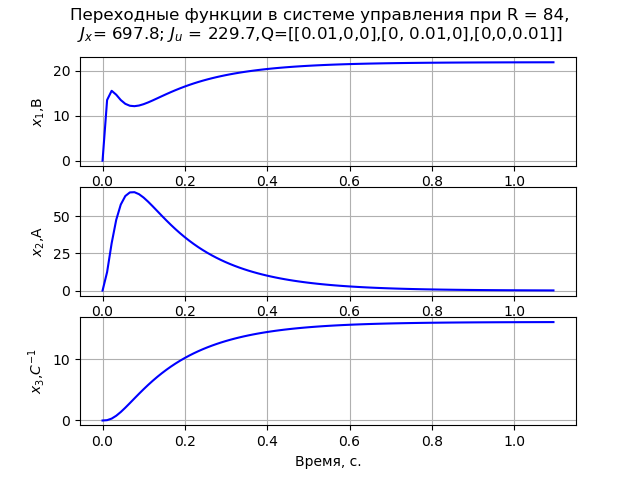 Fig. 1
Fig. 1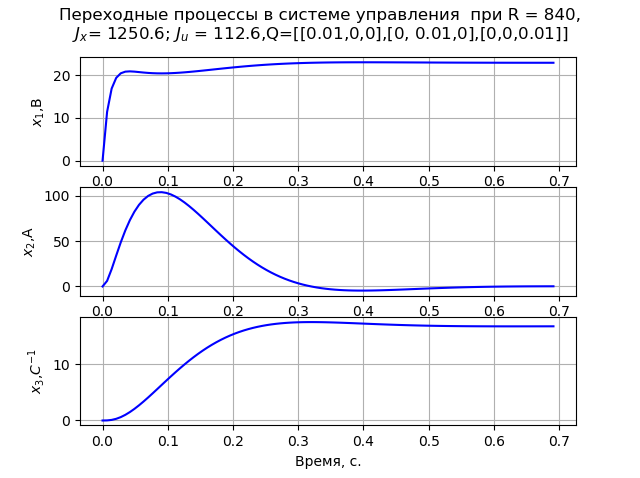 Fig. 2
Fig. 2Dengan pemilihan matriks R dan Q yang tepat, dimungkinkan untuk mengurangi arus awal motor ke nilai yang dapat diterima sama dengan (2–2,5) In (Gbr. 3). Misalnya, dengan R = 840 dan
Q = ([[[0,01,0,0]], [0,0,88,0], [0,0,0,01]], nilainya 292 A, dan waktu proses transisi dalam kondisi ini adalah 1,57 dtk.

Gbr.3
Dalam semua kasus yang dipertimbangkan, umpan balik pada tegangan dan arus negatif, dan pada kecepatan, positif, yang tidak diinginkan sesuai dengan persyaratan stabilitas. Selain itu, sistem yang disintesis adalah astatic untuk tugas dan statis untuk beban. Oleh karena itu, kami mempertimbangkan sintesis pengontrol PI di ruang keadaan dengan variabel status tambahan
x4 - Koefisien transfer integrator.
Kami mewakili informasi awal dalam bentuk matriks:
A = \ begin {bmatrix} & -100 & 0 & 0 & 0 \\ & 143.678 & -16.667 & -195.402 & 0 \\ & 0 & 1.046 & 0 & 0 \\ & 0 & 0 & 1 & 0 \ end {bmatrix}; B = \ begin {bmatrix} 2300 \\ 0 \\ 0 \\ 0 \\ end {bmatrix}; C = eye (4)); D = 0A = \ begin {bmatrix} & -100 & 0 & 0 & 0 \\ & 143.678 & -16.667 & -195.402 & 0 \\ & 0 & 1.046 & 0 & 0 \\ & 0 & 0 & 1 & 0 \ end {bmatrix}; B = \ begin {bmatrix} 2300 \\ 0 \\ 0 \\ 0 \\ end {bmatrix}; C = eye (4)); D = 0Transien tugas yang sesuai dengan kriteria MO diperoleh pada R = 100, q11 = q22 = q33 = 0,001 dan q44 = 200. Gambar 4 menunjukkan transien variabel keadaan yang mengkonfirmasi astatisme sistem dengan tugas dan beban.
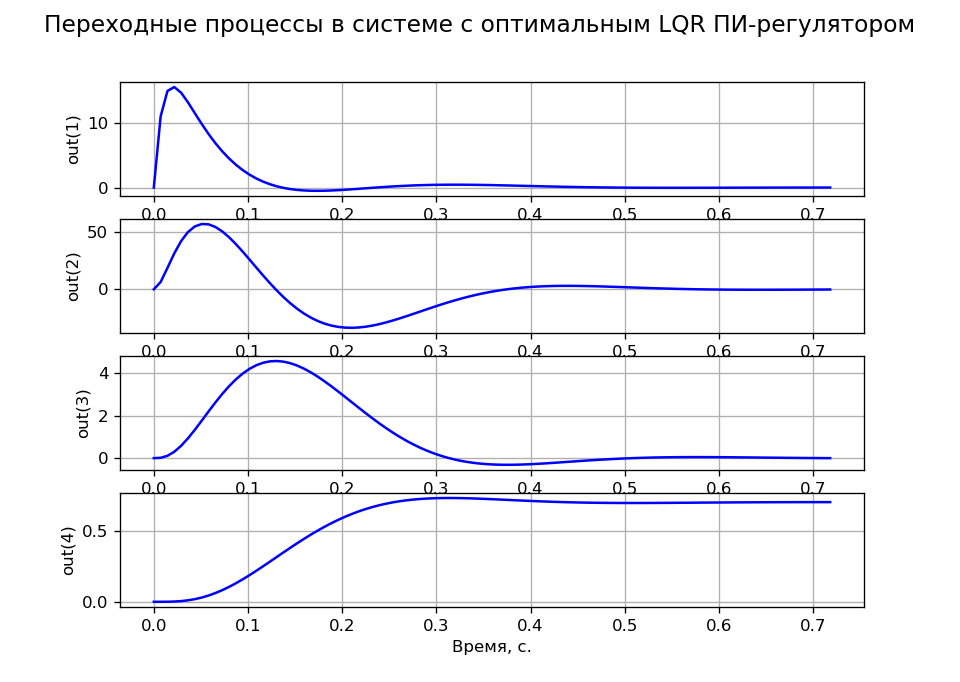 Fig. 4
Fig. 4Untuk menentukan matriks K, Pustaka Sistem Kontrol Python memiliki dua fungsi K = acker (A, B, s) dan K = place (A, B, s), di mana s adalah vektor - deretan kutub yang diinginkan dari fungsi transfer sistem kontrol loop tertutup. Perintah pertama hanya dapat digunakan untuk sistem dengan satu input di u untuk n≤5. Yang kedua tidak memiliki batasan seperti itu, tetapi multiplisitas kutub tidak boleh melebihi pangkat matriks B. Contoh penggunaan operator acker () ditunjukkan dalam daftar dan dalam (Gbr. 5).
 Fig. 5
Fig. 5Kesimpulan
Implementasi LQR-optimasi drive listrik yang diberikan dalam publikasi, dengan mempertimbangkan penggunaan fungsi lqr () dan lyap () baru, akan memungkinkan kita untuk meninggalkan penggunaan program berlisensi MATLAB ketika mempelajari bagian yang sesuai dari teori kontrol.
Contoh optimasi LQR di pesawat terbang (LA)
(contoh diambil dari publikasi oleh Astrom dan Mruray, Bab 5 [8] dan diselesaikan oleh penulis artikel dalam hal mengganti fungsi lqr () dan mengurangi terminologi menjadi yang diterima secara umum)Bagian teoretis, teori singkat, optimasi LQR telah dipertimbangkan di atas, jadi mari kita beralih ke analisis kode dengan komentar yang sesuai:
Pustaka yang diperlukan dan fungsi pengontrol LQR. from scipy.linalg import*
Kondisi awal dan matriks dasar model A, B, C, D. xe = [0, 0, 0, 0, 0, 0];
Kami membangun input dan output yang sesuai dengan perubahan langkah demi langkah pada posisi xy. Vektor xd dan yd sesuai dengan kondisi stabil yang diinginkan dalam sistem. Matriks Cx dan Cy adalah output yang sesuai dari model. Untuk menggambarkan dinamika sistem, kami menggunakan sistem persamaan vektor-matriks:
\ left \ {\ begin {matrix} xdot = Kapak + Bu => xdot = (A-BK) x + xd \\ u = -K (x-xd) \\ y = Cx \\ \ end {matrix} \ benar
\ left \ {\ begin {matrix} xdot = Kapak + Bu => xdot = (A-BK) x + xd \\ u = -K (x-xd) \\ y = Cx \\ \ end {matrix} \ benar
Dinamika loop tertutup dapat dimodelkan menggunakan fungsi step (), untuk K \ cdot xd dan K \ cdot xd sebagai vektor input, di mana:
xd = matrix([[1], [0], [0], [0], [0], [0]]); yd = matrix([[0], [1], [0], [0], [0], [0]]);
Pustaka 0.8.1 kontrol saat ini hanya mendukung sebagian fungsi SISO Matlab untuk membuat pengontrol umpan balik, oleh karena itu, untuk membaca data dari pengontrol, oleh karena itu diperlukan untuk membuat vektor indeks lat (), alt () untuk dinamika lateral -x dan vertikal -y.
lat = (0,2,3,5); alt = (1,4);
Grafik ditampilkan secara berurutan, satu untuk setiap tugas.
figure(); title(" x y") plot(Tx.T, Yx.T, '-', Ty.T, Yy.T, '--'); plot([0, 10], [1, 1], 'k-'); axis([0, 10, -0.1, 1.4]); ylabel(' '); xlabel(''); legend(('x', 'y'), loc='lower right'); grid() show()
Bagan: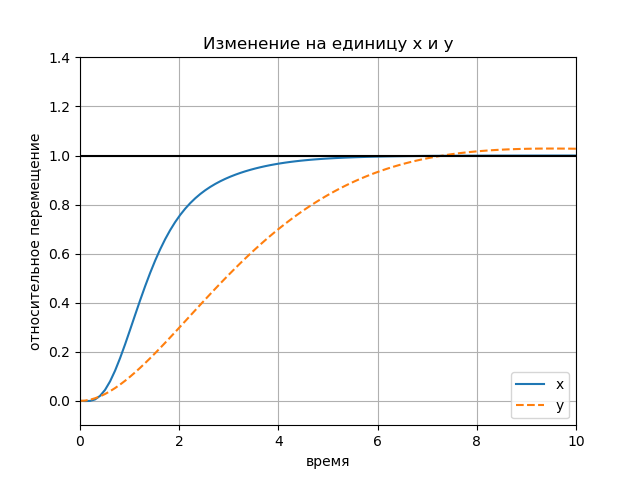
Pengaruh amplitudo dari tindakan input Bagan: Bagan:
Bagan: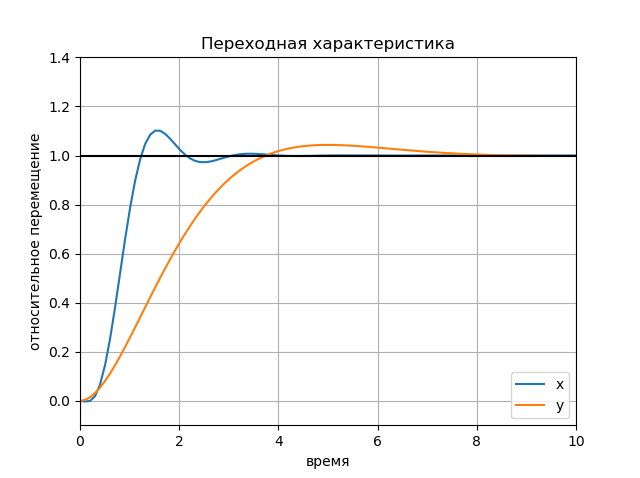
Respons transien berbasis fisik Bagan: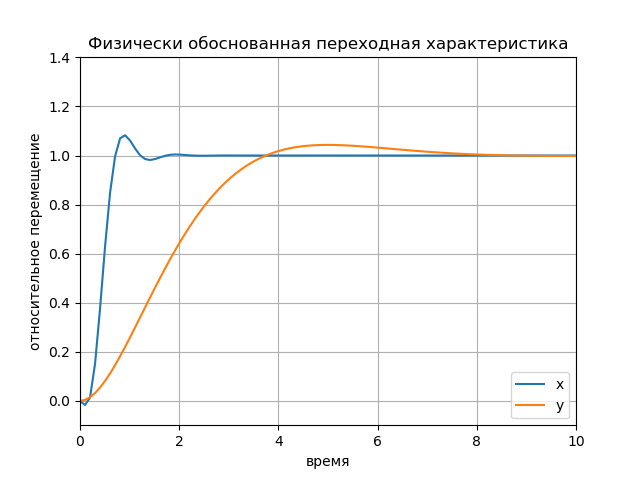
Kesimpulan:
Implementasi optimasi LQR dalam pesawat yang disajikan dalam publikasi, dengan mempertimbangkan penggunaan fungsi lqr () baru, akan memungkinkan kita untuk meninggalkan penggunaan program berlisensi MATLAB ketika mempelajari bagian yang sesuai dari teori kontrol.
Referensi
1.
Matematika pada jari: pengontrol linear-kuadratik.2.
Ruang keadaan dalam masalah merancang sistem kontrol yang optimal.3.
Menggunakan Pustaka Sistem Kontrol Python untuk merancang sistem kontrol otomatis.4.
Perpustakaan Sistem Kontrol Python.5.
Python - tidak dapat mengimpor modul slycot ke spyder (RuntimeError & ImportError).6.
Perpustakaan Sistem Kontrol Python.7.
Kriteria untuk kontrol optimal dan optimalisasi lqr dalam drive listrik.