Bagaimana teka-teki anak-anak membantu mengungkap rahasia magnetisme

Magnet sudah akrab bagi manusia sejak zaman kuno, tetapi fisika feromagnetisme tetap menjadi misteri. Sekarang sebuah teka-teki yang akrab membawa fisikawan lebih dekat untuk menjawab pertanyaan

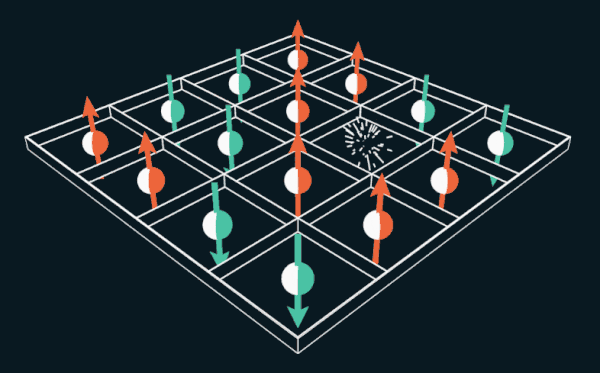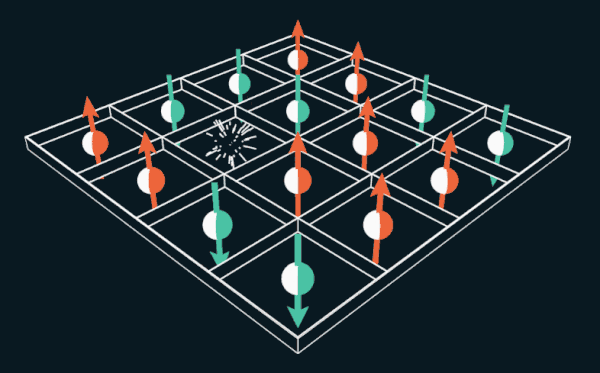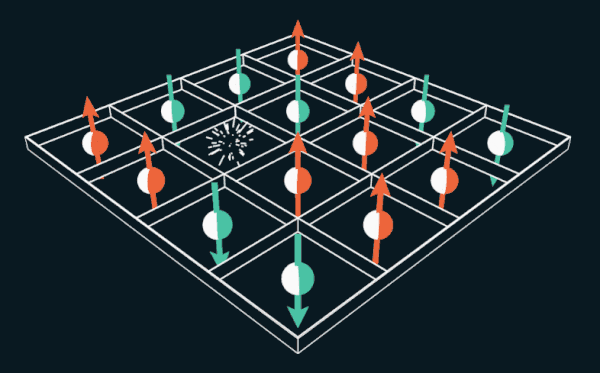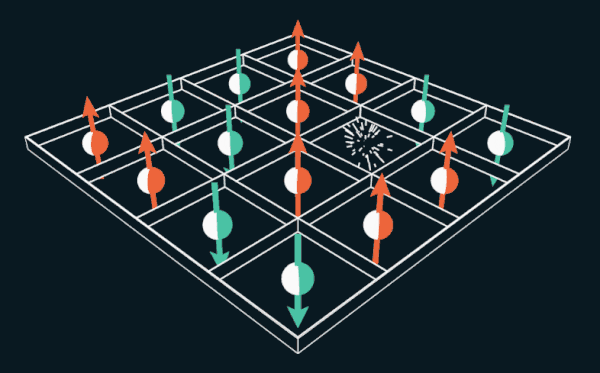Gim 15 menawarkan pemain untuk memindahkan ubin bernomor dalam kisi. Jika Anda mengganti angka dengan spin elektron, puzzle dapat digunakan untuk menjelaskan cara kerja magnet permanen.

Selama beberapa bulan di tahun 1880, seluruh wilayah Amerika Serikat menyerah pada kecanduan, analog yang sebelumnya tidak pernah dilihat siapa pun. ”Epidemi telah meletus di seluruh negeri,” tulis majalah The Weekly News-Demokrat di Imperia, Kansas, 12 Maret 1880. “Seluruh kota terpikat, orang-orang kehilangan tidur dan menjadi gila.” Epidemi menyebar ke Eropa, dan bahkan mencapai Australia dengan Selandia Baru.

Penyakit ini telah menjadi gairah baru: mengecilkan mainan puzzle mekanik sederhana "15". Itu masih diketahui, dan terdiri dari bidang persegi 4x4 di mana Anda dapat memindahkan 15 ubin bernomor untuk mengaturnya secara berurutan.

Menurut standar sekarang, gim ini tampak kuno, tetapi pada tahun 1880 gim ini berada di puncak popularitas. "Tidak ada anak yang bisa menolak hiburan seperti itu, tidak ada orang dewasa akan begitu kuat atau sombong untuk melepaskan pesonanya," tulis surat kabar itu. Dan kekecewaan mungkin berasal dari fakta yang telah terbukti secara matematis bahwa hanya setengah dari konfigurasi puzzle ini yang dapat diselesaikan dengan sukses (yang mungkin tidak diketahui oleh mereka yang berada di bawah pengaruhnya).

Hari ini, hampir 140 tahun kemudian, minat pada permainan "15" telah dihidupkan kembali, tetapi kali ini tidak bertindak sebagai pengalih perhatian, tetapi sebagai cara untuk memahami teka-teki yang tampaknya tidak berhubungan dan jauh lebih rumit: bagaimana magnet bekerja.

Magnet permanen, seperti magnet yang tergantung di pintu kulkas Anda, tertarik oleh fenomena seperti feromagnetisme . Dalam feromagnet, spin elektron disejajarkan, dan bersama-sama mereka menghasilkan medan magnet. Lebih tepatnya, logam seperti besi, kobalt, dan nikel menunjukkan magnetisme pita, karena elektronnya dapat bergerak bebas di dalam material. Setiap elektron memiliki momen magnetnya sendiri, tetapi untuk memahami bagaimana dan mengapa semua momen ini berbaris dalam magnet, perlu untuk menghitung interaksi kuantum antara semua elektron, yang terlalu sulit untuk dilakukan.

"Zona magnetisme sebenarnya adalah salah satu tantangan terbesar dalam fisika benda terkondensasi teoretis," kata Wai Lee, seorang ahli fisika di Universitas Johns Hopkins.

Namun, Lee dan dua mahasiswa pascasarjana, Eric Bobrov dan Keaton Stewbis, mungkin sedikit lebih dekat untuk menyelesaikan masalah ini. Dengan menggunakan teka-teki matematika "15", mereka memperluas teorema terkenal yang menggambarkan keadaan ideal magnetisme zona. Dalam analisis baru mereka, yang diterbitkan dalam Physical Review B, mereka memperluas teorema untuk menjelaskan sistem yang lebih luas dan lebih realistis, yang berpotensi mengarah pada model magnet yang lebih akurat.

"Ini pekerjaan yang hebat," kata Daniel Arovas , seorang ahli fisika di University of California, San Diego. "Saya terutama menyukai pekerjaan ini karena fakta bahwa ada terlalu sedikit hasil rinci tentang magnet zona dan mereka terlalu terfragmentasi."

Lubang melompat

Pada tingkat paling dasar, elektron dalam logam harus mematuhi dua batasan utama. Pertama, mereka semua dibebankan secara negatif, oleh karena itu mereka saling tolak. Kedua, elektron diharuskan untuk mematuhi apa yang disebut prinsip Pauli, yang mendalilkan bahwa dua partikel [dengan putaran setengah bilangan bulat / kira-kira. trans.] tidak boleh berada dalam status kuantum yang sama. Ini berarti bahwa elektron dengan putaran yang sama - sebanding dengan momen magnetik elektron - tidak dapat menempati keadaan yang sama dalam atom logam. Dan dua elektron dengan putaran berlawanan bisa.

Ternyata cara paling sederhana untuk memuaskan tolakan timbal balik dan keterbatasan prinsip Pauli untuk sekelompok elektron adalah secara terpisah dan meluruskan putaran - sebagai akibatnya bahan menjadi feromagnetik.

Namun, ini hanya gambaran sederhana. Fisikawan tidak dapat membangun model terperinci dari penampilan pola terorganisir dari putaran yang sejajar dari interaksi kuantum yang tak terhitung jumlahnya di antara masing-masing elektron. Sebagai contoh, seperti yang dijelaskan Lee, fungsi gelombang sebuah elektron - deskripsi matematis kompleks dari sifat-sifat kuantumnya - dapat dikacaukan dengan fungsi gelombang dari elektron lain. Untuk benar-benar memahami bagaimana perilaku partikel individu mengarah pada munculnya fenomena kolektif seperti feromagnetisme, Anda harus memantau fungsi gelombang masing-masing elektron dalam sistem, sementara itu terus-menerus mengubah fungsi gelombang masing-masing elektron yang tersisa dalam proses interaksi mereka. Dalam praktiknya, keterjeratan yang meluas ini tidak memungkinkan untuk menuliskan persamaan lengkap dan komprehensif yang diperlukan untuk menggambarkan feromagnetisme.

Alih-alih, fisikawan, termasuk Lee, mencoba mengumpulkan informasi dengan mempelajari model-model sederhana dan ideal yang menggambarkan fisika di balik feromagnetisme. Secara khusus, karya terbarunya memperluas penemuan penting yang dibuat lebih dari 50 tahun yang lalu.

Pada pertengahan 1960-an, dua fisikawan dari sisi yang berlawanan dari dunia menunjukkan bukti independen yang membuktikan mengapa elektron harus sejajar dan menciptakan keadaan feromagnetik. David Tules, yang saat itu seorang ahli fisika di Universitas Cambridge yang akhirnya akan memenangkan Hadiah Nobel 2016, dan Yosuke Nagaoka, seorang ahli fisika di Universitas Nagoya yang sedang mengunjungi Universitas California di San Diego pada waktu itu, menerbitkan bukti mereka masing-masing pada tahun 1965 dan 1966. . Hasilnya, disebut teorema Nagaoki-Tules (atau hanya teorema Nagaoki), didasarkan pada sistem elektron ideal yang terletak pada kisi atom. Jadi, meskipun tidak menjelaskan perilaku magnet nyata, itu tetap penting, menunjukkan untuk pertama kalinya secara prinsip mengapa spin elektron harus disejajarkan. Dan karena analisis mereka adalah bukti matematis, mereka akurat, tidak dibebani dengan perkiraan khas fisika.

Untuk memahami teorema, bayangkan sebuah kisi persegi dua dimensi. Setiap node dapat menempatkan dua elektron dengan putaran berlawanan, tetapi teorema menyarankan bahwa untuk menempatkan dua elektron di satu tempat akan membutuhkan energi yang tak terbatas. Ini memastikan bahwa hanya satu elektron yang akan berada di setiap tempat. Dalam konfigurasi ini, setiap elektron dapat mengarahkan putarannya ke atas atau ke bawah. Mereka tidak harus menyelaraskan, jadi sistem seperti itu seharusnya tidak menjadi feromagnet.


Wai Lee, seorang ahli fisika di Universitas Johns Hopkins

Sekarang kita menghapus satu elektron. Akibatnya, akan ada tempat kosong yang disebut lubang. Elektron tetangga dapat menyelinap ke dalam lubang, meninggalkan ruang kosong baru. Elektron lain dapat pindah ke tempat kosong baru, meninggalkan lubang lain di belakang. Dalam contoh ini, sebuah lubang, pada kenyataannya, melompat dari satu tempat ke tempat lain, bergerak di sekitar grid. Thules dan Nagaoka menemukan bahwa dalam kasus ini, ketika satu lubang ditambahkan, elektron akan sejajar secara spontan. Mereka membuktikan bahwa itu adalah keadaan dengan energi paling sedikit, keadaan feromagnet.

Arovas menjelaskan bahwa agar suatu sistem masuk ke keadaan dengan energi terendah, sebuah lubang harus dapat bergerak bebas tanpa mengganggu konfigurasi spin elektron - proses semacam itu akan membutuhkan energi tambahan. Tetapi ketika sebuah lubang bergerak, elektron juga harus bergerak. Agar elektron dapat bergerak tanpa mengganggu konfigurasi putaran, mereka harus disejajarkan.

"Teorema Nagaoka adalah salah satu dari sedikit contoh yang secara matematis dapat membuktikan masing-masing kasus feromagnetisme," kata Masaki Oshikawa , seorang ahli fisika di Universitas Tokyo. "Tapi dari sudut pandang fisika, semua ini sangat buatan."

Sebagai contoh, elektron membutuhkan banyak energi untuk mengatasi tolakan timbal balik mereka dan menetap di satu tempat - tetapi tidak terbatas, seperti teorema yang dibutuhkan. Selain itu, gambar yang diambil oleh Nagaoka dan Tules hanya berlaku untuk kisi-kisi sederhana: kisi dua dimensi yang terdiri dari kotak atau segitiga, atau kisi kubik tiga dimensi. Di alam, feromagnetisme muncul di banyak logam dengan struktur dari setiap jenis.

Jika teorema Nagaoka-Tules benar-benar menjelaskan feromagnetisme, maka itu harus berlaku untuk semua kisi. Orang-orang mengira itu, kata Lee. "Tapi tidak ada yang memberikan bukti nyata dan jelas." Ya, masih.

Ubin dengan punggung

Pada tahun 1989, Hal Tasaki, seorang ahli fisika di Universitas Gakushuin Jepang, memperluas teorema ini untuk menemukan bahwa teorema itu akan berlaku selama kisi memiliki sifat matematika sebagai konektivitas. Ambil wadah sederhana dari sebuah kisi persegi dengan satu lubang bergerak. Jika, dengan menggerakkan lubang, Anda dapat mereproduksi konfigurasi spin, menjaga jumlah elektron, dengan putaran diarahkan ke atas dan ke bawah, maka kondisi koneksi terpenuhi.

Tetapi terlepas dari kisi-kisi persegi dan segitiga, dan kubus tiga dimensi, tidak jelas apakah kondisi yang terhubung akan terpenuhi dalam kasus lain - dan, oleh karena itu, seberapa luas teorema ini dapat diterapkan.

Untuk mengatasi masalah ini, Lee mulai dengan kotak sarang lebah heksagonal. Murid-muridnya, Bobrov dan Stubis, yang mengerjakan tugas ini, menyadari bahwa itu menyerupai mania abad XIX: teka-teki "15". Tukar label ubin dari angka ke punggung, atas dan bawah, dan puzzle menjadi setara dengan feromagnet Nagaoki, dengan lubang bergerak di sepanjang kisi elektron.

Teka-teki diperbolehkan ketika Anda memiliki kesempatan untuk mendistribusikan kembali ubin dalam urutan apa pun, yang sepenuhnya bertepatan dengan kondisi konektivitas. Jadi pertanyaan apakah kondisi konektivitas terpenuhi untuk kisi yang diberikan menjadi pertanyaan apakah mungkin untuk memecahkan teka-teki yang setara pada kisi struktur seperti itu.

Ternyata pada tahun 1974 ahli matematika Richard Wilson, sekarang bekerja di California Institute of Technology, memecahkan masalah ini dengan merangkum dan memecahkan teka-teki "15" untuk semua grid. Sebagai bagian dari bukti, ia menunjukkan bahwa pada hampir semua kisi yang tidak dapat dipisahkan (di mana semua node tetap terhubung bahkan setelah menghapus salah satunya), Anda dapat memindahkan ubin dan mendapatkan konfigurasi apa pun, selama jumlah gerakan tetap genap. Satu-satunya pengecualian adalah bahwa poligon tunggal lebih besar dari segitiga, dan sesuatu yang disebut "graph ullnull", di mana simpul di pusat segi enam terhubung ke dua simpul yang berlawanan.

Para peneliti dapat langsung menerapkan bukti Wilson ke teorema Nagaoka-Tules. Mereka membuktikan bahwa kondisi konektivitas memuaskan untuk sistem elektron dan lubang tunggal pada hampir semua kisi, termasuk struktur umum seperti sarang lebah dua dimensi dan kisi berbentuk berlian tiga dimensi. Dua pengecualian - poligon lebih besar dari segitiga, dan grafik graphnull - dalam hal apa pun, tidak terjadi pada feromagnet nyata.

Lubang ledakan

Menggunakan teka-teki "15" adalah pendekatan yang segar dan berpotensi berbuah, kata Sriram Shastri , seorang ahli fisika di University of California di Santa Cruz. "Saya suka fakta bahwa dia membawa untuk bekerja bahasa baru, satu set koneksi baru dengan teori graf," katanya. "Saya pikir ini adalah koneksi yang kaya - di masa depan mungkin menjadi sumber ide yang kaya." Tetapi, meskipun penelitian mengambil langkah maju yang signifikan, masalah tetap ada.

Salah satu komplikasi adalah bahwa teorema Nagaoki-Tules tidak selalu bekerja ketika sebuah lubang yang bergerak perlu mengambil sejumlah langkah ganjil saat bergerak di sepanjang kisi, kata Shastri. Mungkin masalah yang paling mencolok adalah bahwa teorema membutuhkan keberadaan satu lubang - tidak lebih, tidak kurang. Namun, logam penuh dengan lubang, mereka sering menempati hingga setengah dari kisi.

Tetapi fisikawan mencoba menggeneralisasi teorema untuk sistem dengan banyak lubang. Menggunakan metode numerik, fisikawan telah menunjukkan bahwa feromagnetisme Nagaoki tampaknya bekerja untuk kisi persegi ukuran terbatas, hingga 30% di antaranya adalah lubang. Dalam karya saat ini, para peneliti menerapkan teknik analisis yang tepat untuk sarang lebah dua dimensi dan kisi berbentuk berlian tiga dimensi. Feromagnetisme Nagaoki, tampaknya, ada selama jumlah lubang tidak melebihi jumlah node kisi dalam derajat 1/2 untuk sel, dan pada tingkat 2/5 untuk kisi berbentuk berlian.

Solusi tepat ini dapat menghasilkan model magnet zona yang lebih lengkap. "Ini hanya satu langkah kecil menuju pengaturan titik awal matematika yang ketat untuk penelitian masa depan," kata Lee.