Persamaan Diferensial Biasa Neural
Proporsi proses yang signifikan dijelaskan oleh persamaan diferensial, ini mungkin merupakan evolusi sistem fisik dari waktu ke waktu, kondisi medis pasien, karakteristik dasar pasar saham, dll. Data tentang proses-proses semacam itu sifatnya konsisten dan berkelanjutan, dalam arti bahwa pengamatan hanyalah manifestasi dari semacam keadaan yang terus berubah.
Ada juga tipe lain dari data serial, itu adalah data diskrit, misalnya, data tugas NLP. Keadaan dalam data tersebut bervariasi secara terpisah: dari satu karakter atau kata ke yang lain.
Sekarang kedua jenis data serial tersebut biasanya diproses oleh jaringan rekursif, meskipun sifatnya berbeda dan tampaknya memerlukan pendekatan yang berbeda.
Satu artikel yang sangat menarik disajikan pada
konferensi NIPS terakhir, yang dapat membantu menyelesaikan masalah ini. Para penulis mengusulkan pendekatan yang mereka sebut
ODE Neural .
Di sini saya mencoba mereproduksi dan merangkum hasil artikel ini untuk membuat perkenalan dengan idenya sedikit lebih mudah. Tampak bagi saya bahwa arsitektur baru ini mungkin menemukan tempat dalam alat standar ilmuwan data bersama dengan jaringan convolutional dan berulang.
Gambar 1: Backpropagation gradien kontinu membutuhkan pemecahan persamaan diferensial augmented kembali dalam waktu.
Panah mewakili penyesuaian gradien yang diperbanyak mundur dengan gradien dari pengamatan.
Ilustrasi dari artikel asli.
Pernyataan masalah
Biarkan ada proses yang mematuhi beberapa ODE yang tidak diketahui dan biarkan ada beberapa (berisik) pengamatan di sepanjang lintasan proses
Cara menemukan perkiraan

fungsi speaker

?
Pertama, pertimbangkan tugas yang lebih sederhana: hanya ada 2 pengamatan, di awal dan di akhir lintasan,

.
Evolusi sistem dimulai dari keadaan

tepat waktu

dengan beberapa fungsi dinamika parameter menggunakan metode evolusi sistem ODE. Setelah sistem dalam keadaan baru

, itu dibandingkan dengan negara

dan perbedaan di antara mereka diminimalkan dengan memvariasikan parameter

fungsi dinamika.
Atau, lebih formal, pertimbangkan meminimalkan fungsi kerugian

:
Untuk meminimalkan

, Anda perlu menghitung gradien untuk semua parameternya:

. Untuk melakukan ini, Anda harus terlebih dahulu menentukan caranya

tergantung pada keadaan setiap saat

:

disebut keadaan
adjoint , dinamikanya diberikan oleh persamaan diferensial lain, yang dapat dianggap sebagai analog kontinu dari diferensiasi fungsi kompleks (
aturan rantai ):
Output dari formula ini dapat ditemukan di lampiran artikel asli.
Vektor dalam artikel ini harus dianggap sebagai vektor huruf kecil, meskipun artikel asli menggunakan representasi baris dan kolom.Memecahkan perbedaan (4) kembali dalam waktu, kami memperoleh ketergantungan pada keadaan awal

:
Untuk menghitung gradien sehubungan dengan

dan

, Anda bisa menganggap mereka bagian dari negara. Kondisi ini disebut
augmented . Dinamika keadaan ini secara sepele diperoleh dari dinamika aslinya:
Kemudian kondisi konjugasi ke kondisi augmented ini:
Gradient Augmented Dynamics:
Persamaan diferensial dari kondisi augmented terkonjugasi dari rumus (4) kemudian:
Memecahkan ODE ini kembali dalam hasil waktu:
Ada apa dengan
memberikan gradien di semua parameter input ke
ODES solve ODE
solver .
Semua gradien (10), (11), (12), (13) dapat dihitung bersama dalam satu panggilan
ODESolve dengan dinamika keadaan augmented terkonjugasi (9).
 Ilustrasi dari artikel asli.
Ilustrasi dari artikel asli.Algoritma di atas menjelaskan propagasi balik gradien dari solusi ODE untuk pengamatan berturut-turut.
Dalam kasus beberapa pengamatan pada satu lintasan, semuanya dihitung dengan cara yang sama, tetapi pada saat pengamatan, kebalikan dari gradien terdistribusi harus disesuaikan dengan gradien dari pengamatan saat ini, seperti yang ditunjukkan pada
Gambar 1 .
Implementasi
Kode di bawah ini adalah implementasi
ODE Neural saya . Saya melakukannya murni untuk pemahaman yang lebih baik tentang apa yang terjadi. Namun, sangat dekat dengan apa yang diterapkan dalam
repositori penulis artikel. Ini berisi semua kode yang perlu Anda pahami di satu tempat, juga sedikit lebih banyak dikomentari. Untuk aplikasi dan eksperimen nyata, masih lebih baik untuk menggunakan implementasi penulis dari artikel asli.
import math import numpy as np from IPython.display import clear_output from tqdm import tqdm_notebook as tqdm import matplotlib as mpl import matplotlib.pyplot as plt %matplotlib inline import seaborn as sns sns.color_palette("bright") import matplotlib as mpl import matplotlib.cm as cm import torch from torch import Tensor from torch import nn from torch.nn import functional as F from torch.autograd import Variable use_cuda = torch.cuda.is_available()
Pertama, Anda perlu menerapkan metode apa pun untuk evolusi sistem ODE. Demi kesederhanaan, metode Euler diimplementasikan di sini, meskipun metode eksplisit atau implisit cocok.
def ode_solve(z0, t0, t1, f): """ - """ h_max = 0.05 n_steps = math.ceil((abs(t1 - t0)/h_max).max().item()) h = (t1 - t0)/n_steps t = t0 z = z0 for i_step in range(n_steps): z = z + h * f(z, t) t = t + h return z
Ini juga menjelaskan superclass dari fungsi dinamika parameter dengan beberapa metode yang berguna.
Pertama: Anda harus mengembalikan semua parameter yang fungsinya tergantung dalam bentuk vektor.
Kedua: perlu untuk menghitung dinamika augmented. Dinamika ini tergantung pada gradien fungsi parameter dalam hal parameter dan input data. Agar tidak harus mendaftarkan gradien dengan masing-masing tangan untuk setiap arsitektur baru, kita akan menggunakan metode
torch.autograd.grad .
class ODEF(nn.Module): def forward_with_grad(self, z, t, grad_outputs): """Compute f and a df/dz, a df/dp, a df/dt""" batch_size = z.shape[0] out = self.forward(z, t) a = grad_outputs adfdz, adfdt, *adfdp = torch.autograd.grad( (out,), (z, t) + tuple(self.parameters()), grad_outputs=(a), allow_unused=True, retain_graph=True )
Kode di bawah ini menjelaskan propagasi maju dan mundur untuk
ODE Neural . Hal ini diperlukan untuk memisahkan kode ini dari
torch.nn.Module utama dalam bentuk fungsi
torch.autograd.Fungsi karena dalam yang terakhir Anda dapat menerapkan metode
backpropagation sewenang-wenang, tidak seperti modul. Jadi ini hanya penopang.
Fitur ini mendasari seluruh pendekatan
ODE Neural .
class ODEAdjoint(torch.autograd.Function): @staticmethod def forward(ctx, z0, t, flat_parameters, func): assert isinstance(func, ODEF) bs, *z_shape = z0.size() time_len = t.size(0) with torch.no_grad(): z = torch.zeros(time_len, bs, *z_shape).to(z0) z[0] = z0 for i_t in range(time_len - 1): z0 = ode_solve(z0, t[i_t], t[i_t+1], func) z[i_t+1] = z0 ctx.func = func ctx.save_for_backward(t, z.clone(), flat_parameters) return z @staticmethod def backward(ctx, dLdz): """ dLdz shape: time_len, batch_size, *z_shape """ func = ctx.func t, z, flat_parameters = ctx.saved_tensors time_len, bs, *z_shape = z.size() n_dim = np.prod(z_shape) n_params = flat_parameters.size(0)
Sekarang untuk kenyamanan, bungkus fungsi ini dalam
nn.Module .
class NeuralODE(nn.Module): def __init__(self, func): super(NeuralODE, self).__init__() assert isinstance(func, ODEF) self.func = func def forward(self, z0, t=Tensor([0., 1.]), return_whole_sequence=False): t = t.to(z0) z = ODEAdjoint.apply(z0, t, self.func.flatten_parameters(), self.func) if return_whole_sequence: return z else: return z[-1]
Aplikasi
Pemulihan fungsi dinamika nyata (verifikasi pendekatan)
Sebagai tes dasar, sekarang mari kita periksa apakah
Neural ODE dapat mengembalikan fungsi sebenarnya dari dinamika menggunakan data pengamatan.
Untuk melakukan ini, pertama-tama kita menentukan fungsi dinamika ODE, mengembangkan lintasan berdasarkan itu, dan kemudian mencoba mengembalikannya dari fungsi dinamika parameter acak.
Pertama, mari kita periksa kasus paling sederhana dari ODE linier. Fungsi dinamika hanyalah aksi dari sebuah matriks.
Fungsi yang dilatih ditentukan oleh matriks acak.
Selanjutnya, dinamika sedikit lebih canggih (tanpa gif, karena proses belajarnya tidak begitu indah :))
Fungsi pembelajaran di sini adalah jaringan yang sepenuhnya terhubung dengan satu lapisan tersembunyi.
Kode class LinearODEF(ODEF): def __init__(self, W): super(LinearODEF, self).__init__() self.lin = nn.Linear(2, 2, bias=False) self.lin.weight = nn.Parameter(W) def forward(self, x, t): return self.lin(x)
Fungsi dinamika hanyalah sebuah matriks
class SpiralFunctionExample(LinearODEF): def __init__(self): matrix = Tensor([[-0.1, -1.], [1., -0.1]]) super(SpiralFunctionExample, self).__init__(matrix)
Matriks yang diparameterisasi secara acak
class RandomLinearODEF(LinearODEF): def __init__(self): super(RandomLinearODEF, self).__init__(torch.randn(2, 2)/2.)
Dinamika untuk lintasan yang lebih canggih
class TestODEF(ODEF): def __init__(self, A, B, x0): super(TestODEF, self).__init__() self.A = nn.Linear(2, 2, bias=False) self.A.weight = nn.Parameter(A) self.B = nn.Linear(2, 2, bias=False) self.B.weight = nn.Parameter(B) self.x0 = nn.Parameter(x0) def forward(self, x, t): xTx0 = torch.sum(x*self.x0, dim=1) dxdt = torch.sigmoid(xTx0) * self.A(x - self.x0) + torch.sigmoid(-xTx0) * self.B(x + self.x0) return dxdt
Belajar dinamika dalam bentuk jaringan yang terhubung penuh
class NNODEF(ODEF): def __init__(self, in_dim, hid_dim, time_invariant=False): super(NNODEF, self).__init__() self.time_invariant = time_invariant if time_invariant: self.lin1 = nn.Linear(in_dim, hid_dim) else: self.lin1 = nn.Linear(in_dim+1, hid_dim) self.lin2 = nn.Linear(hid_dim, hid_dim) self.lin3 = nn.Linear(hid_dim, in_dim) self.elu = nn.ELU(inplace=True) def forward(self, x, t): if not self.time_invariant: x = torch.cat((x, t), dim=-1) h = self.elu(self.lin1(x)) h = self.elu(self.lin2(h)) out = self.lin3(h) return out def to_np(x): return x.detach().cpu().numpy() def plot_trajectories(obs=None, times=None, trajs=None, save=None, figsize=(16, 8)): plt.figure(figsize=figsize) if obs is not None: if times is None: times = [None] * len(obs) for o, t in zip(obs, times): o, t = to_np(o), to_np(t) for b_i in range(o.shape[1]): plt.scatter(o[:, b_i, 0], o[:, b_i, 1], c=t[:, b_i, 0], cmap=cm.plasma) if trajs is not None: for z in trajs: z = to_np(z) plt.plot(z[:, 0, 0], z[:, 0, 1], lw=1.5) if save is not None: plt.savefig(save) plt.show() def conduct_experiment(ode_true, ode_trained, n_steps, name, plot_freq=10):
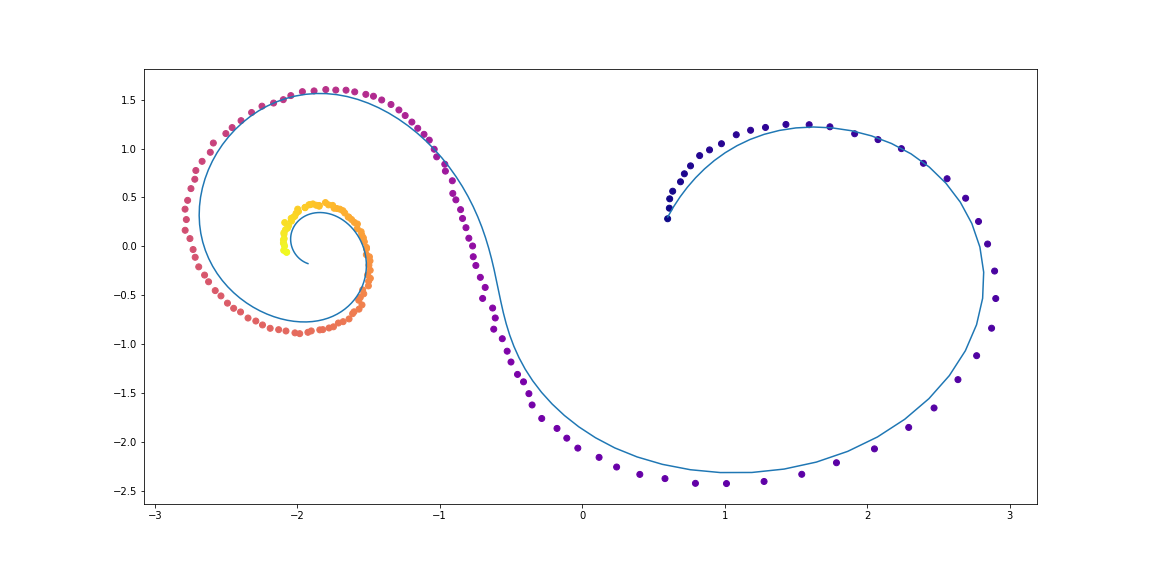
Seperti yang Anda lihat,
Neural ODE cukup bagus dalam memulihkan dinamika. Artinya, konsep secara keseluruhan berfungsi.
Sekarang periksa masalah yang sedikit lebih rumit (MNIST, haha).
ODE Neural terinspirasi oleh ResNets
Di ResNet'ax, status laten berubah sesuai dengan rumus
dimana

Apakah nomor blok dan

ini adalah fungsi yang dipelajari oleh lapisan di dalam blok.
Dalam batasnya, jika kita mengambil jumlah blok yang tak terbatas dengan langkah-langkah yang lebih kecil, kita mendapatkan dinamika kontinu dari lapisan tersembunyi dalam bentuk ODE, seperti apa yang ada di atas.
Mulai dari lapisan input

kita dapat mendefinisikan layer output

sebagai solusi untuk ODE ini pada waktu T.
Sekarang kita bisa menghitung

sebagai parameter terdistribusi (
dibagi ) antara semua blok sangat kecil.
Memvalidasi Arsitektur ODE Neural pada MNIST
Pada bagian ini, kami akan menguji kemampuan
Neural ODE untuk digunakan sebagai komponen dalam arsitektur yang lebih akrab.
Secara khusus, kami akan mengganti blok residual dengan
Neural ODE di pengklasifikasi MNIST.
Kode def norm(dim): return nn.BatchNorm2d(dim) def conv3x3(in_feats, out_feats, stride=1): return nn.Conv2d(in_feats, out_feats, kernel_size=3, stride=stride, padding=1, bias=False) def add_time(in_tensor, t): bs, c, w, h = in_tensor.shape return torch.cat((in_tensor, t.expand(bs, 1, w, h)), dim=1) class ConvODEF(ODEF): def __init__(self, dim): super(ConvODEF, self).__init__() self.conv1 = conv3x3(dim + 1, dim) self.norm1 = norm(dim) self.conv2 = conv3x3(dim + 1, dim) self.norm2 = norm(dim) def forward(self, x, t): xt = add_time(x, t) h = self.norm1(torch.relu(self.conv1(xt))) ht = add_time(h, t) dxdt = self.norm2(torch.relu(self.conv2(ht))) return dxdt class ContinuousNeuralMNISTClassifier(nn.Module): def __init__(self, ode): super(ContinuousNeuralMNISTClassifier, self).__init__() self.downsampling = nn.Sequential( nn.Conv2d(1, 64, 3, 1), norm(64), nn.ReLU(inplace=True), nn.Conv2d(64, 64, 4, 2, 1), norm(64), nn.ReLU(inplace=True), nn.Conv2d(64, 64, 4, 2, 1), ) self.feature = ode self.norm = norm(64) self.avg_pool = nn.AdaptiveAvgPool2d((1, 1)) self.fc = nn.Linear(64, 10) def forward(self, x): x = self.downsampling(x) x = self.feature(x) x = self.norm(x) x = self.avg_pool(x) shape = torch.prod(torch.tensor(x.shape[1:])).item() x = x.view(-1, shape) out = self.fc(x) return out func = ConvODEF(64) ode = NeuralODE(func) model = ContinuousNeuralMNISTClassifier(ode) if use_cuda: model = model.cuda() import torchvision img_std = 0.3081 img_mean = 0.1307 batch_size = 32 train_loader = torch.utils.data.DataLoader( torchvision.datasets.MNIST("data/mnist", train=True, download=True, transform=torchvision.transforms.Compose([ torchvision.transforms.ToTensor(), torchvision.transforms.Normalize((img_mean,), (img_std,)) ]) ), batch_size=batch_size, shuffle=True ) test_loader = torch.utils.data.DataLoader( torchvision.datasets.MNIST("data/mnist", train=False, download=True, transform=torchvision.transforms.Compose([ torchvision.transforms.ToTensor(), torchvision.transforms.Normalize((img_mean,), (img_std,)) ]) ), batch_size=128, shuffle=True ) optimizer = torch.optim.Adam(model.parameters()) def train(epoch): num_items = 0 train_losses = [] model.train() criterion = nn.CrossEntropyLoss() print(f"Training Epoch {epoch}...") for batch_idx, (data, target) in tqdm(enumerate(train_loader), total=len(train_loader)): if use_cuda: data = data.cuda() target = target.cuda() optimizer.zero_grad() output = model(data) loss = criterion(output, target) loss.backward() optimizer.step() train_losses += [loss.item()] num_items += data.shape[0] print('Train loss: {:.5f}'.format(np.mean(train_losses))) return train_losses def test(): accuracy = 0.0 num_items = 0 model.eval() criterion = nn.CrossEntropyLoss() print(f"Testing...") with torch.no_grad(): for batch_idx, (data, target) in tqdm(enumerate(test_loader), total=len(test_loader)): if use_cuda: data = data.cuda() target = target.cuda() output = model(data) accuracy += torch.sum(torch.argmax(output, dim=1) == target).item() num_items += data.shape[0] accuracy = accuracy * 100 / num_items print("Test Accuracy: {:.3f}%".format(accuracy)) n_epochs = 5 test() train_losses = [] for epoch in range(1, n_epochs + 1): train_losses += train(epoch) test() import pandas as pd plt.figure(figsize=(9, 5)) history = pd.DataFrame({"loss": train_losses}) history["cum_data"] = history.index * batch_size history["smooth_loss"] = history.loss.ewm(halflife=10).mean() history.plot(x="cum_data", y="smooth_loss", figsize=(12, 5), title="train error")
Testing... 100% 79/79 [00:01<00:00, 45.69it/s] Test Accuracy: 9.740% Training Epoch 1... 100% 1875/1875 [01:15<00:00, 24.69it/s] Train loss: 0.20137 Testing... 100% 79/79 [00:01<00:00, 46.64it/s] Test Accuracy: 98.680% Training Epoch 2... 100% 1875/1875 [01:17<00:00, 24.32it/s] Train loss: 0.05059 Testing... 100% 79/79 [00:01<00:00, 46.11it/s] Test Accuracy: 97.760% Training Epoch 3... 100% 1875/1875 [01:16<00:00, 24.63it/s] Train loss: 0.03808 Testing... 100% 79/79 [00:01<00:00, 45.65it/s] Test Accuracy: 99.000% Training Epoch 4... 100% 1875/1875 [01:17<00:00, 24.28it/s] Train loss: 0.02894 Testing... 100% 79/79 [00:01<00:00, 45.42it/s] Test Accuracy: 99.130% Training Epoch 5... 100% 1875/1875 [01:16<00:00, 24.67it/s] Train loss: 0.02424 Testing... 100% 79/79 [00:01<00:00, 45.89it/s] Test Accuracy: 99.170%
Setelah pelatihan yang sangat kasar selama hanya 5 era dan 6 menit pelatihan, model tersebut telah mencapai kesalahan pengujian kurang dari 1%. Kita dapat mengatakan bahwa
ODE Neural terintegrasi dengan baik
sebagai komponen ke dalam jaringan yang lebih tradisional.
Dalam artikel mereka, penulis juga membandingkan pengelompokan ini (ODE-Net) dengan jaringan yang terhubung penuh reguler, dengan ResNet dengan arsitektur yang sama, dan dengan arsitektur yang sama persis, di mana gradien merambat langsung melalui operasi dalam
ODESolve (tanpa metode gradien konjugat) ( RK-Net).
Ilustrasi dari artikel asli.Menurut mereka, jaringan 1-layer yang terhubung sepenuhnya dengan jumlah parameter yang sama dengan
Neural ODE memiliki kesalahan yang jauh lebih tinggi dalam pengujian, ResNet dengan banyak kesalahan yang sama memiliki lebih banyak parameter, dan RK-Net tanpa metode gradien konjugasi memiliki kesalahan yang sedikit lebih tinggi dan dengan konsumsi memori yang meningkat secara linear (semakin kecil kesalahan yang diizinkan, semakin banyak langkah yang harus diambil
ODESolve , yang meningkatkan konsumsi memori secara linear dengan jumlah langkah).
Para penulis menggunakan metode Runge-Kutta implisit dengan ukuran langkah adaptif dalam implementasinya, tidak seperti metode Euler yang lebih sederhana di sini. Mereka juga mempelajari beberapa properti dari arsitektur baru.
Fitur ODE-Net (NFE Forward - jumlah kalkulasi fungsi secara langsung)
Ilustrasi dari artikel asli.- (a) Mengubah tingkat kesalahan numerik yang dapat diterima mengubah jumlah langkah dalam distribusi langsung.
- (B) Waktu yang dihabiskan untuk distribusi langsung sebanding dengan jumlah perhitungan fungsi.
- (C) Jumlah perhitungan fungsi untuk propagasi kembali adalah sekitar setengah dari propagasi langsung, yang menunjukkan bahwa metode gradien konjugat mungkin lebih efisien secara komputasi daripada menyebarkan gradien langsung melalui ODESolve .
- (d) Ketika ODE-Net menjadi semakin terlatih, ini membutuhkan lebih banyak dan lebih banyak komputasi dari suatu fungsi (langkah yang semakin kecil), mungkin beradaptasi dengan meningkatnya kompleksitas model.
Fungsi Generatif Tersembunyi untuk Pemodelan Rangkaian Waktu
Neural ODE cocok untuk memproses data serial terus menerus bahkan ketika jalurnya terletak di ruang tersembunyi yang tidak diketahui.
Di bagian ini, kami akan bereksperimen
dan mengubah generasi urutan berkelanjutan menggunakan
Neural ODE , dan melihat ruang tersembunyi yang dipelajari.
Para penulis juga membandingkan ini dengan urutan serupa yang dihasilkan oleh jaringan berulang.
Percobaan di sini sedikit berbeda dari contoh terkait dalam repositori penulis, di sini ada serangkaian lintasan yang lebih beragam.
Data
Data pelatihan terdiri dari spiral acak, setengahnya searah jarum jam, dan yang kedua berlawanan arah jarum jam. Lebih lanjut, sampel acak diambil dari spiral ini, diproses oleh model pengulangan pengkodean dalam arah yang berlawanan, sehingga menimbulkan keadaan awal yang tersembunyi, yang kemudian berevolusi, menciptakan lintasan di ruang tersembunyi. Jalur laten ini kemudian dipetakan ke ruang data dan dibandingkan dengan sampel berikutnya. Dengan demikian, model belajar untuk menghasilkan lintasan yang mirip dengan dataset.
Contoh dataset spiralVAE sebagai model generatif
Model generatif melalui prosedur pengambilan sampel:
Yang dapat dilatih menggunakan pendekatan auto-encoder variasional.
- Pergi melalui encoder berulang melalui urutan waktu kembali pada waktunya untuk mendapatkan parameter
 ,
,  distribusi posterior variasional, dan kemudian sampel darinya:
distribusi posterior variasional, dan kemudian sampel darinya:
- Dapatkan lintasan tersembunyi:
- Memetakan jalur tersembunyi ke jalur dalam data menggunakan jaringan saraf lain:

- Maksimalkan penilaian batas bawah validitas (ELBO) untuk jalur sampel:
Dan dalam kasus distribusi posterior Gaussian

dan tingkat kebisingan yang diketahui

:
Grafik perhitungan model ODE tersembunyi dapat direpresentasikan sebagai berikut
Ilustrasi dari artikel asli.Model ini kemudian dapat diuji untuk mengetahui bagaimana interpolasi jalur hanya menggunakan pengamatan awal.
KodeTentukan model
class RNNEncoder(nn.Module): def __init__(self, input_dim, hidden_dim, latent_dim): super(RNNEncoder, self).__init__() self.input_dim = input_dim self.hidden_dim = hidden_dim self.latent_dim = latent_dim self.rnn = nn.GRU(input_dim+1, hidden_dim) self.hid2lat = nn.Linear(hidden_dim, 2*latent_dim) def forward(self, x, t):
Generasi dataset
t_max = 6.29*5 n_points = 200 noise_std = 0.02 num_spirals = 1000 index_np = np.arange(0, n_points, 1, dtype=np.int) index_np = np.hstack([index_np[:, None]]) times_np = np.linspace(0, t_max, num=n_points) times_np = np.hstack([times_np[:, None]] * num_spirals) times = torch.from_numpy(times_np[:, :, None]).to(torch.float32)
Pelatihan
vae = ODEVAE(2, 64, 6) vae = vae.cuda() if use_cuda: vae = vae.cuda() optim = torch.optim.Adam(vae.parameters(), betas=(0.9, 0.999), lr=0.001) preload = False n_epochs = 20000 batch_size = 100 plot_traj_idx = 1 plot_traj = orig_trajs[:, plot_traj_idx:plot_traj_idx+1] plot_obs = samp_trajs[:, plot_traj_idx:plot_traj_idx+1] plot_ts = samp_ts[:, plot_traj_idx:plot_traj_idx+1] if use_cuda: plot_traj = plot_traj.cuda() plot_obs = plot_obs.cuda() plot_ts = plot_ts.cuda() if preload: vae.load_state_dict(torch.load("models/vae_spirals.sd")) for epoch_idx in range(n_epochs): losses = [] train_iter = gen_batch(batch_size) for x, t in train_iter: optim.zero_grad() if use_cuda: x, t = x.cuda(), t.cuda() max_len = np.random.choice([30, 50, 100]) permutation = np.random.permutation(t.shape[0]) np.random.shuffle(permutation) permutation = np.sort(permutation[:max_len]) x, t = x[permutation], t[permutation] x_p, z, z_mean, z_log_var = vae(x, t) z_var = torch.exp(z_log_var) kl_loss = -0.5 * torch.sum(1 + z_log_var - z_mean**2 - z_var, -1) loss = 0.5 * ((x-x_p)**2).sum(-1).sum(0) / noise_std**2 + kl_loss loss = torch.mean(loss) loss /= max_len loss.backward() optim.step() losses.append(loss.item()) print(f"Epoch {epoch_idx}") frm, to, to_seed = 0, 200, 50 seed_trajs = samp_trajs[frm:to_seed] ts = samp_ts[frm:to] if use_cuda: seed_trajs = seed_trajs.cuda() ts = ts.cuda() samp_trajs_p = to_np(vae.generate_with_seed(seed_trajs, ts)) fig, axes = plt.subplots(nrows=3, ncols=3, figsize=(15, 9)) axes = axes.flatten() for i, ax in enumerate(axes): ax.scatter(to_np(seed_trajs[:, i, 0]), to_np(seed_trajs[:, i, 1]), c=to_np(ts[frm:to_seed, i, 0]), cmap=cm.plasma) ax.plot(to_np(orig_trajs[frm:to, i, 0]), to_np(orig_trajs[frm:to, i, 1])) ax.plot(samp_trajs_p[:, i, 0], samp_trajs_p[:, i, 1]) plt.show() print(np.mean(losses), np.median(losses)) clear_output(wait=True) spiral_0_idx = 3 spiral_1_idx = 6 homotopy_p = Tensor(np.linspace(0., 1., 10)[:, None]) vae = vae if use_cuda: homotopy_p = homotopy_p.cuda() vae = vae.cuda() spiral_0 = orig_trajs[:, spiral_0_idx:spiral_0_idx+1, :] spiral_1 = orig_trajs[:, spiral_1_idx:spiral_1_idx+1, :] ts_0 = samp_ts[:, spiral_0_idx:spiral_0_idx+1, :] ts_1 = samp_ts[:, spiral_1_idx:spiral_1_idx+1, :] if use_cuda: spiral_0, ts_0 = spiral_0.cuda(), ts_0.cuda() spiral_1, ts_1 = spiral_1.cuda(), ts_1.cuda() z_cw, _ = vae.encoder(spiral_0, ts_0) z_cc, _ = vae.encoder(spiral_1, ts_1) homotopy_z = z_cw * (1 - homotopy_p) + z_cc * homotopy_p t = torch.from_numpy(np.linspace(0, 6*np.pi, 200)) t = t[:, None].expand(200, 10)[:, :, None].cuda() t = t.cuda() if use_cuda else t hom_gen_trajs = vae.decoder(homotopy_z, t) fig, axes = plt.subplots(nrows=2, ncols=5, figsize=(15, 5)) axes = axes.flatten() for i, ax in enumerate(axes): ax.plot(to_np(hom_gen_trajs[:, i, 0]), to_np(hom_gen_trajs[:, i, 1])) plt.show() torch.save(vae.state_dict(), "models/vae_spirals.sd")
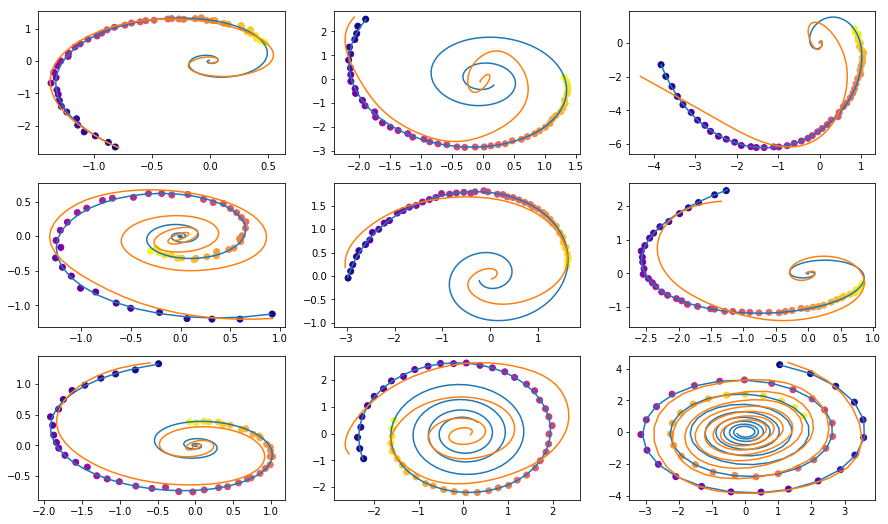
— , .
.. . .
, - - .
Neural ODE .
. , , (, ), .
, , .
,
.
, ,
, , , .
:
( ) ( ) ;
-X «» ( ) «» ( ).
bekemax .
Neural ODEs . !