Mengelompokkan titik akses nirkabel menggunakan metode k-means

Visualisasi dan analisis data saat ini banyak digunakan dalam industri telekomunikasi. Secara khusus, analisis ini sangat tergantung pada penggunaan data geospasial. Mungkin ini disebabkan oleh fakta bahwa jaringan telekomunikasi sendiri tersebar secara geografis. Dengan demikian, analisis dispersi semacam itu bisa sangat bernilai.

Data

Untuk mengilustrasikan algoritma pengelompokan k-means, kami akan menggunakan database geografis untuk WiFi publik gratis di New York. Dataset tersedia di NYC Open Data. Secara khusus, algoritma klaster k-means digunakan untuk membentuk cluster penggunaan WiFi berdasarkan data lintang dan bujur.

Data lintang dan bujur diekstraksi dari kumpulan data itu sendiri menggunakan bahasa pemrograman R:

#1. Prepare data newyork<-read.csv("NYC_Free_Public_WiFi_03292017.csv") attach(newyork) newyorkdf<-data.frame(newyork$LAT,newyork$LON) 

Ini adalah sepotong data:

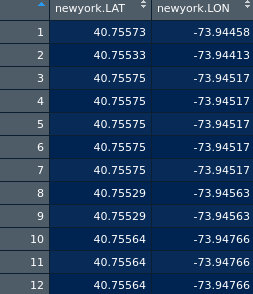
Kami menentukan jumlah cluster

Selanjutnya, kami menentukan jumlah cluster menggunakan kode di bawah ini, yang menunjukkan hasilnya dalam grafik.

 #2. Determine number of clusters wss <- (nrow(newyorkdf)-1)*sum(apply(newyorkdf,2,var)) for (i in 2:20) wss[i] <- sum(kmeans(newyorkdf, centers=i)$withinss) plot(1:20, wss, type="b", xlab="Number of Clusters", ylab="Within groups sum of squares") 

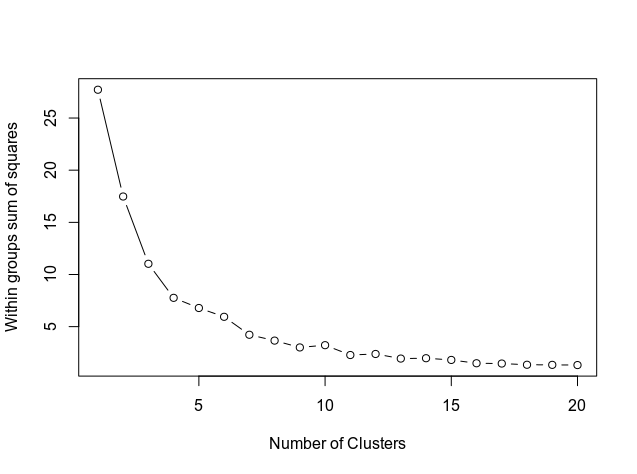
Grafik menunjukkan bagaimana kurva sejajar di sekitar 11. Oleh karena itu, ini adalah jumlah cluster yang akan digunakan dalam model k-means.

Analisis K-means

Analisis K-means dilakukan:

 #3. K-Means Cluster Analysis set.seed(20) fit <- kmeans(newyorkdf, 11) # 11 cluster solution # get cluster means aggregate(newyorkdf,by=list(fit$cluster),FUN=mean) # append cluster assignment newyorkdf <- data.frame(newyorkdf, fit$cluster) newyorkdf newyorkdf$fit.cluster <- as.factor(newyorkdf$fit.cluster) library(ggplot2) ggplot(newyorkdf, aes(x=newyork.LON, y=newyork.LAT, color = newyorkdf$fit.cluster)) + geom_point() 

Dataset newyorkdf berisi informasi tentang lintang, bujur, dan label klaster:
> newyorkdf
newyork.lat newyork.lon fit.cluster
1 40.75573 -73.94458 1
2 40.75533 -73.94413 1
3 40.75575 -73.94517 1
4 40.75575 -73.94517 1
5 40.75575 -73.94517 1
6 40.75575 -73.94517 1
...
80 40.84832 -73.82075 11

Ini ilustrasi yang jelas:



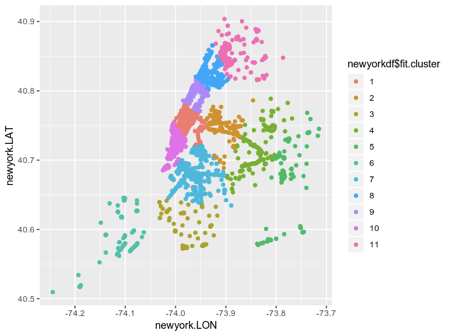
Ilustrasi ini bermanfaat, tetapi visualisasi akan menjadi lebih berharga jika Anda overlay pada peta New York sendiri.

 # devtools::install_github("zachcp/nycmaps") library(nycmaps) map(database="nyc") #this should also work with ggplot and ggalt nyc <- map_data("nyc") gg <- ggplot() gg <- gg + geom_map( data=nyc, map=nyc, aes(x=long, y=lat, map_id=region)) gg + geom_point(data = newyorkdf, aes(x = newyork.LON, y = newyork.LAT), colour = newyorkdf$fit.cluster, alpha = .5) + ggtitle("New York Public WiFi") 

Jenis pengelompokan ini memberikan gagasan yang sangat baik tentang struktur jaringan WiFi di kota. Ini menunjukkan bahwa wilayah geografis yang ditandai oleh cluster 1 menunjukkan banyak lalu lintas WiFi. Di sisi lain, lebih sedikit koneksi di cluster 6 dapat menunjukkan lalu lintas WiFi yang rendah.

K-Means clustering saja tidak memberi tahu kami mengapa lalu lintas untuk cluster tertentu tinggi atau rendah. Misalnya, ketika cluster 6 memiliki kepadatan populasi yang tinggi, tetapi kecepatan internet yang rendah menghasilkan koneksi yang lebih sedikit.

Namun, algoritma pengelompokan ini memberikan titik awal yang sangat baik untuk analisis lebih lanjut dan memfasilitasi pengumpulan informasi tambahan. Misalnya, dengan menggunakan peta ini sebagai contoh, Anda dapat membuat hipotesis tentang masing-masing kelompok geografis. Artikel asli ada di sini .