Tugas dari buku teks sekolah II

Bagian I
Bagian II
Bagian III

Artikel ini membahas metode memperkirakan kisaran nilai yang diterima dan hubungan metode ini dengan tugas yang berisi modul.

Ketika memecahkan beberapa masalah, perlu untuk mempertimbangkan rentang nilai yang diinginkan.

Pertimbangkan metode estimasi untuk menyelesaikan ketidaksetaraan.

Misalkan harga per unit barang dapat berkisar dari 5 hingga 10 RUB. Memberi batas atas berarti menentukan nilai maksimum yang dapat diambil kuantitas yang diinginkan. Untuk dua unit barang, harga yang tidak melebihi 10, estimasi atas adalah 10 + 10 = 20 .

Pertimbangkan masalah dari profil profil masalah MI Bashmakova
37. Estimasi yang diketahui untuk variabel $$$x$ dan$$ $ inline $ y: 0 <x <5, 2 <y <3. $ inline $

Berikan nilai tertinggi untuk ekspresi berikut:
1. $$$2x + 3tahun$
2. $$$xy$

5. $$$\ frac {1} {y}$
6. $$$\ frac {x} {y}$

8. $$$x-y$
9. $$$3x-2tahun$


Secara umum, analisis jumlah sangat kecil menggunakan kriteria evaluasi. Modul (sebagai lingkungan) menemukan aplikasi dalam definisi batas.

$$$$ menampilkan $$ \ kiri | x_ {n} -a \ kanan | <\ varepsilon $$ menampilkan $$

Pertimbangkan contoh dari "Kursus kalkulus diferensial dan integral" 363 (6)

Mudah untuk mengatur divergensi baris

$$

$$\ sum \ frac {1} {\ sqrt {n}} = 1+ \ frac {1} {\ sqrt {2}} + \ frac {1} {\ sqrt {3}} + ... + \ frac {1} {\ sqrt {n}} + ...$$

Bahkan, sejak anggotanya berkurang, jumlah parsial ke-n

$$$$ menampilkan $$ 1+ \ frac {1} {\ sqrt {2}} + ... + \ frac {1} {\ sqrt {n}}> n \ cdot \ frac {1} {\ sqrt {n }} = \ sqrt {n} $$ menampilkan $$

dan tumbuh tanpa batas dengan $$$n$ .

Untuk membuktikan itu $$$1+ \ frac {1} {\ sqrt {2}} + ... + \ frac {1} {\ sqrt {n}}$ sungguh lebih $$$\ sqrt {n}$ , Anda harus membuat taksiran yang lebih rendah dari ungkapan ini. Kami mendapatkan sistem ketidaksetaraan

$$$$ menampilkan $$ \ kiri \ {\! \ mulai {sejajar} & \ frac {1} {\ sqrt {n-1}}> \ frac {1} {\ sqrt {n}} \\ & \ frac { 1} {\ sqrt {n-2}}> \ frac {1} {\ sqrt {n}} \\ & \ frac {1} {\ sqrt {n-3}}> \ frac {1} {\ sqrt {n}} \\ & ... \ end {aligned} \ kanan. $$ tampilan $$

Setelah menambahkan semua ketidaksetaraan sistem ini, kita dapatkan

$$$$ menampilkan $$ 1+ \ frac {1} {\ sqrt {2}} + \ frac {1} {\ sqrt {3}} + ... + \ frac {1} {\ sqrt {n}}> \ frac {1} {\ sqrt {n}} + \ frac {1} {\ sqrt {n}} + \ frac {1} {\ sqrt {n}} + ... + \ frac {1} {\ sqrt {n}} = n \ cdot \ frac {1} {\ sqrt {n}} $$ menampilkan $$

Ini adalah bukti bahwa seri ini berbeda.

Untuk rangkaian harmonik, metode ini tidak berfungsi, karena $$$n$ seri harmonik parsial parsial

$$$$ menampilkan $$ 1+ \ frac {1} {2} + \ frac {1} {3} + ... + \ frac {1} {n}> n \ cdot \ frac {1} {n} = 1 $$ menampilkan $$

Kembali ke tugas

38. Hitung jumlahnya ("Tugas untuk anak-anak dari 5 hingga 15 tahun")

$$

$$\ frac {1} {1 \ cdot2} + \ frac {1} {2 \ cdot3} + \ frac {1} {3 \ cdot4} + ... + \ frac {1} {99 \ cdot100}$$

(dengan kesalahan tidak lebih dari 1% dari jawabannya)

Estimasi teratas dari seri ini $$$\ frac {n} {n + 1}$ memberikan angka 1.

Jatuhkan istilah pertama $$$\ frac {1} {1 \ cdot2}$

(define series_sum_1 ( lambda (n) (if (= n 0) 0 (+ (/ 1.0 (* (+ n 1.0 )(+ n 2.0))) (series_sum_1(- n 1.0))) ) ) ) (writeln (series_sum_1 10)) (writeln (series_sum_1 100)) (writeln (series_sum_1 1000)) (writeln (series_sum_1 10000)) (writeln (series_sum_1 100000)) (writeln (series_sum_1 1000000)) 

Kami mendapatkan $$$1 - \ frac {1} {1 \ cdot2} = \ frac {1} {2}$
0,4166666666666666363
0.49019607843137253
0,4990019960079833
0,4999000199960005
0,49999000019998724
0,4999990000019941

Anda dapat memeriksa di ideone.com di sini


Jatuhkan dua istilah pertama $$$\ frac {1} {1 \ cdot2} + \ frac {1} {2 \ cdot3}$

 (define series_sum_1 ( lambda (n) (if (= n 0) 0 (+ (/ 1.0 (* (+ n 2.0) (+ n 3.0))) (series_sum_1(- n 1.0))) ) ) ) (series_sum_1 1000000) 

Kami akan mendapatkan 0,33333233333632745
Jumlah sebagian dari seri dibatasi di atas.

Baris positif selalu memiliki jumlah; jumlah ini akan terbatas (dan karenanya seri konvergen) jika jumlah parsial dari seri dibatasi di atas, dan tak terbatas (dan seri diverging) sebaliknya.

Membuang $$$n$ istilah awal dari seri harmonik.
Buktikan (menggunakan batas bawah) itu

$$$$ menampilkan $$ \ frac {1} {n + 1} + \ frac {1} {n + 2} + ... + \ frac {1} {2n}> \ frac {1} {2} $$ tampilkan $$

Jika, membuang dua istilah pertama, sisa anggota rangkaian harmonik dibagi menjadi beberapa kelompok $$$2,4,8, ..., 2 ^ {k-1}, ...$ anggota di masing-masing

$$

$$\ frac {1} {3} + \ frac {1} {4}; \ frac {1} {5} + \ frac {1} {6} + \ frac {1} {7} + \ frac {1} {8}; \ frac {1} {9} + ... \ frac {1} {16}; ...;$$

$$

$$\ frac {1} {2 ^ {k-1} +1} + ... + \ frac {1} {2 ^ {k}}; ...,$$

maka masing-masing jumlah ini secara individual akan lebih besar $$$\ frac {1} {2}$ .
... Kami melihat bahwa jumlah sebagian tidak dapat dibatasi di atas: seri memiliki jumlah yang tak terbatas.

Kami menghitung jumlah parsial yang diperoleh dengan membuang $$$2 ^ {k}$ ketentuan

 #lang racket (* 1.0 (+ 1/3 1/4)) (* 1.0 (+ 1/5 1/6 1/7 1/8)) (* 1.0 (+ 1/9 1/10 1/11 1/12 1/13 1/14 1/15 1/16)) 

Kami mendapatkan:
0,583333333333333434
0.6345238095238095
0,6628718503718504
Kami menulis sebuah program yang menghitung jumlah dari seri harmonik dari $$$\ frac {n} {2}$ sebelumnya $$$n$ dimana $$$n = 2 ^ {k}$ di $$$k \ in \ mathbb {N}$

 #lang racket (define (Hn n ) (define half_arg (/ n 2.0)) (define (series_sum n) (if (= n half_arg ) 0 (+ (/ 1.0 n) (series_sum(- n 1)) ) ) ) (series_sum n) ) (Hn 4) (Hn 8) (Hn 16) (Hn 32) 

Kami mendapatkan:
0,583333333333333333
0.6345238095238095
0,6628718503718504
0.6777662022075267

Anda dapat memeriksa ide daring di tautan
Untuk rentang $$$\ kiri [1 + 2 ^ {70}; 2 ^ {71} \ kanan]$ kami mendapatkan 0,693147 ...
Lihat mojo di Wolfram Cloud di sini .

Algoritma rekursif ini menyebabkan stack overflow cepat.
Artikel ini memiliki contoh penghitungan faktorial menggunakan algoritma iteratif. Kami memodifikasi algoritma berulang ini sehingga menghitung jumlah parsial Hn dalam batas-batas tertentu; sebut batas-batas ini a dan b

 (define (Hn ab) (define (iteration product counter) (if (> counter b) product (iteration (+ product (/ 1.0 counter)) (+ counter 1)))) (iteration 0 a)) 

Batas bawah adalah angka $$$1 + 2 ^ {k}$ , batas atas adalah angka $$$2 \ cdot 2 ^ {k}$
Kami menulis fungsi yang menghitung kekuatan dua

 (define (power_of_two k) (define (iteration product counter) (if (> counter k) product (iteration (* product 2) (+ counter 1)))) (iteration 1 1)) 

Kami akan mengganti (+ 1 (power_of_two k)) sebagai batas bawah, dan menggunakan fungsi (* 2 (power_of_two k)) atau fungsinya yang setara (power_of_two (+ 1 k)) sebagai batas atas
Tulis ulang fungsi Hn

 (define (Hn k) (define a (+ 1 (power_of_two k)) ) (define b (* 2 (power_of_two k)) ) (define (iteration product counter) (if (> counter b) product (iteration (+ product (/ 1.0 counter)) (+ counter 1)))) (iteration 0 a )) 

Sekarang Anda dapat menghitung Hn untuk nilai besar $$$k$ .

Kami menulis dalam C sebuah program yang mengukur waktu yang diperlukan untuk menghitung Hn . Kami akan menggunakan fungsi clock () dari pustaka standar <time.h>
Artikel tentang mengukur waktu prosesor ada di Habré di sini .

 #include <math.h> #include <stdio.h> #include <time.h> int main(int argc, char **argv) { double count; // k  1+2^30  2^31 for(unsigned long long int i=1073741825 ;i<=2147483648 ;i++) { count=count+1.0/i; } printf("Hn = %.12f ", count); double seconds = clock() / (double) CLOCKS_PER_SEC; printf("  %f  \n", seconds); return 0; } 

Biasanya ide online membatasi waktu pelaksanaan menjalankan program hingga lima detik, sehingga program ini hanya dapat diperiksa di beberapa ide online, misalnya di onlinegdb.com atau repl.it
Untuk k dari 1 + 2 ^ 30 hingga 2 ^ 31, waktu pengoperasian adalah ~ 5 detik.
Untuk k dari 1 + 2 ^ 31 ke 2 ^ 32, waktu pengoperasian adalah ~ 10 detik.
Untuk k dari 1 + 2 ^ 32 ke 2 ^ 33, waktu pengoperasian adalah ~ 20 detik.
Untuk k dari 1 + 2 ^ 33 hingga 2 ^ 34, waktu pengoperasian akan ~ 40 detik.
Untuk k dari 1 + 2 ^ 34 hingga 2 ^ 35, waktu pengoperasian akan lebih dari satu menit.
...
Untuk k dari 1 + 2 ^ 45 hingga 2 ^ 46, waktu pengoperasian akan lebih dari 24 jam.

Misalkan untuk k dari 1 + 2 ^ 30 hingga 2 ^ 31, waktu eksekusi algoritma adalah ~ 2 detik.
Kemudian untuk k = 2 ^ (30 + n) waktu eksekusi algoritma adalah 2 ^ n dtk. (di $$$n \ in \ mathbb {N}$ )
Algoritma ini memiliki kompleksitas eksponensial .

Kembali ke modul.
Dalam kalkulus integral, modul digunakan dalam rumus

$$

$$\ int \ frac {1} {x} dx = \ int \ frac {dx} {x} = ln \ kiri | x \ benar | + C$$

Pada Habré ada artikel Logaritma paling alami di mana integral ini dipertimbangkan dan berdasarkan perhitungan angka $$$e$ .

Kehadiran modul dalam formula $$$\ int \ frac {dx} {x} = ln \ kiri | x \ benar | + C$ selanjutnya dibuktikan dalam "Kursus kalkulus diferensial dan integral"

Jika ...$$ $ inline $ x <0 $ inline $ , maka dengan diferensiasi mudah untuk memverifikasi itu $$$\ left [ln (-x) \ right] '= \ frac {1} {x}$

Aplikasi fisik integral $$$\ int \ frac {dx} {x}$

Integral ini digunakan untuk menghitung perbedaan potensial pelat kapasitor silinder.


"Listrik dan magnet":

Perbedaan potensial antara pelat ditemukan oleh integrasi:

$$

$$\ varphi_ {1} - \ varphi_ {2} = \ int \ limit_ {R_ {1}} ^ {R_ {2}} E (r) dr = \ frac {q} {2 \ pi \ varepsilon_ {0} \ varepsilon l} \ int \ limit_ {R_ {1}} ^ {R_ {2}} \ frac {dr} {r} = \ frac {q} {2 \ pi \ varepsilon_ {0} \ varepsilon l} ln \ frac {R_ {2}} {R_ {1}}$$

( $$$R_ {1}$ dan $$$R_ {2}$ - jari-jari pelat bagian dalam dan luar).

Tanda modul tidak digunakan di sini di bawah tanda logaritma natural $$$ln \ kiri | \ frac {R_ {2}} {R_ {1}} \ right |$ karena $$$R_ {1}$ dan $$$R_ {2}$ sangat positif dan bentuk rekaman ini berlebihan.

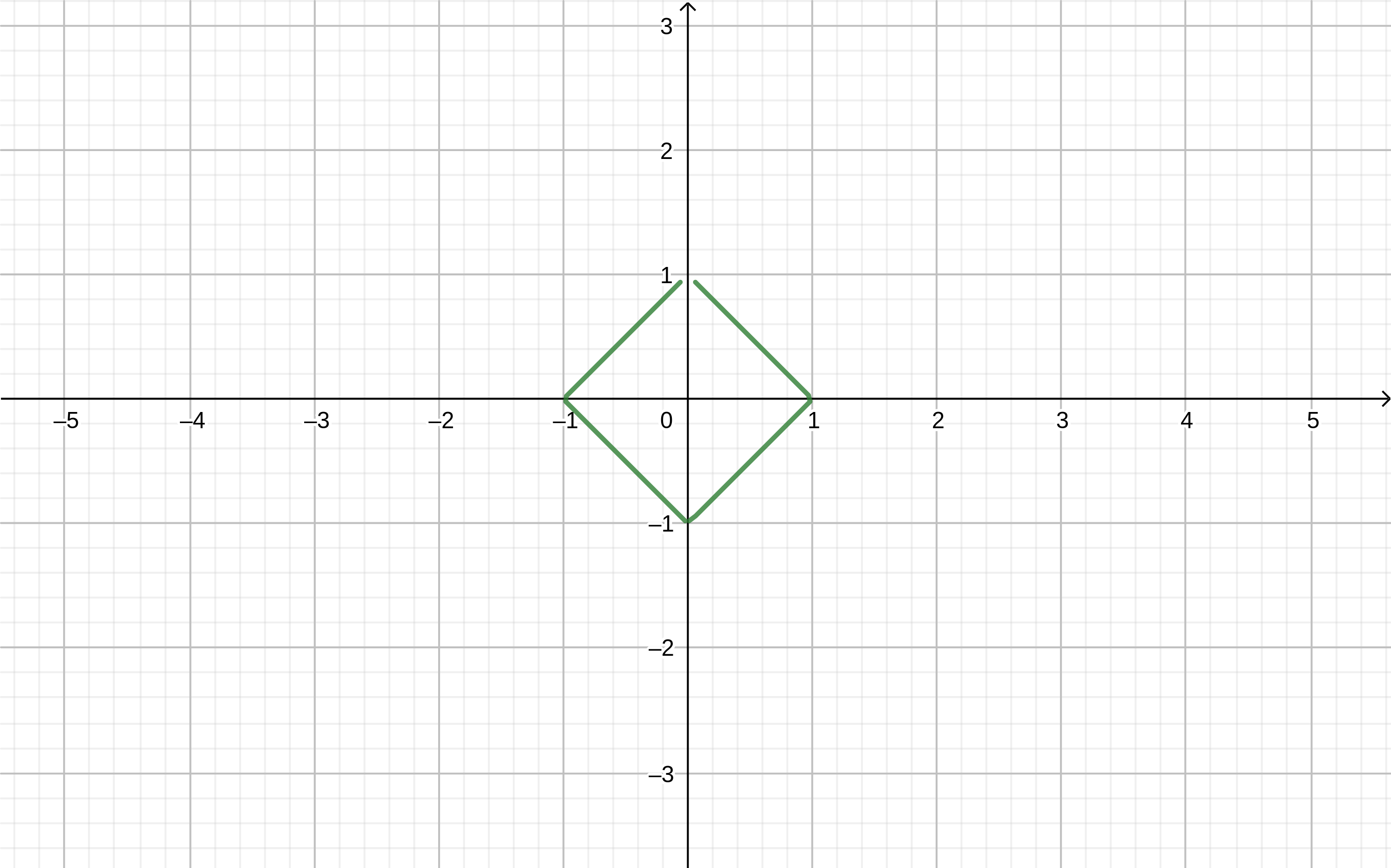
Gambar "Modular"

Dengan menggunakan modul, Anda dapat menggambar berbagai bentuk.

Jika dalam program geogebra tulis rumusnya $$$abs (x) + abs (y) = 1$ kita dapatkan



Anda dapat menggambar bentuk yang lebih kompleks. Mari kita menggambar, misalnya, "kupu-kupu" di awan WolframAlpha

$$

$$\ sum \ frac {\ left | x \ benar | } {n- \ kiri | x \ benar | } + \ frac {\ left | x + n \ kanan | } {n} + \ frac {\ left | x-n \ benar | } {n}$$

Plot [Jumlah [abs (x) / (n-abs (x)) + abs (x + n) / (n) + abs (xn) / (n), {n, 1,20}], {x, -60.60}]
Dalam ungkapan ini $$$n$ terletak pada kisaran dari $$$1$ sebelumnya $$$20$ , $$$x$ terletak pada kisaran dari $$$-60$ sebelumnya $$$60$ .
Tautan ke gambar.

Buku:

"Buku tugas orientasi profil" M.I. Bashmakov
Kursus fisika umum: dalam 3 volume T. 2. "Listrik dan magnet" I.V. Savelyev