
Hai, habrozhiteli! Buku ini didasarkan pada kursus algoritmik online yang dipimpin Tim Rafgarden pada Coursera dan Stanford Lagunita, dan kursus-kursus ini terjadi berkat kuliah yang telah ia berikan kepada mahasiswa di Universitas Stanford selama bertahun-tahun.
Algoritma adalah jantung dan jiwa dari ilmu komputer. Anda tidak dapat melakukannya tanpa mereka, mereka ada di mana-mana - mulai dari routing jaringan dan perhitungan genomik hingga kriptografi dan pembelajaran mesin. "Algoritma Sempurna" akan mengubah Anda menjadi seorang profesional sejati yang akan mengatur tugas dan menyelesaikannya dengan baik dalam kehidupan maupun dalam sebuah wawancara saat mempekerjakan perusahaan IT mana pun. Tim Rafgarden akan berbicara tentang analisis asimptotik, notasi O-besar, algoritma divide and conquer, pengacakan, sortasi dan seleksi. Buku ini ditujukan kepada mereka yang sudah memiliki pengalaman pemrograman. Anda akan pindah ke level baru untuk melihat gambaran besar, untuk memahami konsep level rendah dan nuansa matematika.
* 6.3. Pilih Algoritma
Algoritma RSelect dieksekusi dalam waktu linier untuk setiap input, di mana ekspektasi matematis dikaitkan dengan pilihan acak yang dilakukan oleh algoritma. Apakah pengacakan diperlukan untuk seleksi linier? Pada bagian ini dan selanjutnya, masalah ini diselesaikan dengan menggunakan algoritma linear deterministik untuk masalah pilihan.
Untuk tugas pengurutan, rata-rata runtime dari algoritma QuickSort acak O (n log n) sama dengan algoritma MergeSort deterministik, dan kedua algoritma QuickSort dan MergeSort adalah algoritma yang berguna untuk penggunaan praktis. Di sisi lain, meskipun algoritma seleksi linear deterministik yang dijelaskan dalam bagian ini berfungsi dengan baik dalam praktiknya, itu tidak bersaing dengan algoritma RSelect. Ini terjadi karena dua alasan: karena faktor konstan besar dalam waktu algoritma DSelect dan pekerjaan yang dilakukan oleh algoritma yang terkait dengan alokasi dan pengelolaan RAM tambahan. Namun demikian, ide-ide dalam algoritma ini sangat keren sehingga saya tidak dapat membantu memberitahu Anda tentang mereka.
6.3.1. Ide cemerlang: median median
Algoritma RSelect cepat, karena ada kemungkinan tinggi bahwa elemen dukungan acak akan cukup baik, memberikan pemisahan yang seimbang dari array input setelah pemisahan, apalagi, elemen pendukung yang cukup baik berkembang pesat. Jika kita tidak diizinkan untuk menggunakan pengacakan, lalu bagaimana kita bisa menghitung elemen referensi yang cukup bagus tanpa melakukan terlalu banyak pekerjaan?
Gagasan cerdik dalam pilihan linier deterministik adalah dengan menggunakan "median median" sebagai proksi untuk median sejati. Algoritme menganggap elemen-elemen dari input array sebagai tim olahraga dan mengadakan turnamen sistem gugur dalam dua putaran, yang juara adalah elemen pendukung; lihat juga ara. 6.1.
Babak pertama adalah babak grup dengan elemen di posisi 1–5 dari array input sebagai grup pertama, elemen di posisi 6-10 sebagai kelompok kedua, dan seterusnya. Pemenang babak pertama dari kelompok lima elemen didefinisikan sebagai median elemen (yaitu yang terkecil terkecil). Karena ada
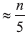
kelompok lima elemen, ada
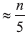
pemenang pertama. (Seperti biasa, kami mengabaikan fraksi untuk kesederhanaan.) Seorang juara turnamen didefinisikan sebagai median dari pemenang babak pertama.
6.3.2. Kodesemu untuk Algoritma DSelect
Bagaimana cara menghitung median median? Implementasi tahap pertama dari turnamen eliminasi sederhana, karena setiap perhitungan median hanya mencakup lima elemen. Misalnya, setiap perhitungan seperti itu dapat dilakukan dengan kekuatan kasar (untuk masing-masing dari lima kemungkinan, periksa secara terperinci apakah itu adalah elemen tengah) atau menggunakan informasi kami tentang masalah penyortiran (bagian 6.1.2). Untuk menerapkan tahap kedua, kami menghitung median dari
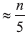
pemenang putaran pertama secara rekursif.
Baris 1–2 dan 6–13 identik dengan algoritma RSelect. Baris 3–5 adalah satu-satunya bagian baru dari algoritma; mereka menghitung median median array input, menggantikan garis dalam algoritma RSelect, yang memilih elemen referensi secara acak.
Baris 3 dan 4 menghitung pemenang putaran pertama turnamen eliminasi, di mana elemen tengah dari masing-masing kelompok terdiri dari lima elemen dihitung menggunakan metode brute force atau algoritma pengurutan, dan menyalin pemenang ini ke array baru C. Baris 5 menghitung juara turnamen dengan menghitung median array C secara rekursif. karena C memiliki panjang (untuk sementara)
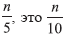
statistik ordinal ke-4 array C. Tidak ada pengacakan yang digunakan pada setiap langkah algoritma
6.3.3. Memahami Algoritma DSelect
Panggilan rekursif ke algoritme DSelect saat menghitung elemen referensi mungkin tampak siklik berbahaya. Untuk memahami apa yang sedang terjadi, mari kita tentukan jumlah total panggilan rekursif.
Jawaban yang benar adalah: (c). Membuang case dasar dan case senang di mana elemen referensi adalah statistik urutan yang diperlukan, algoritma DSelect membuat dua panggilan rekursif. Untuk memahami mengapa, jangan berlebihan; cukup periksa algoritma DSelect kode pseudo baris demi baris. Saluran 5 memiliki satu panggilan rekursif dan satu lagi di saluran 11 atau 13.
Ada dua pertanyaan umum yang membingungkan tentang dua panggilan rekursif ini. Pertama, bukankah fakta bahwa algoritma RSelect hanya membuat satu panggilan rekursif, alasan mengapa ia bekerja lebih cepat daripada algoritma pengurutan kami? Tidakkah DSelect mengabaikan peningkatan ini dengan melakukan dua panggilan rekursif? Bagian 6.4 menunjukkan bahwa karena panggilan rekursif ekstra pada saluran 5 seharusnya hanya menyelesaikan subtugas yang relatif kecil (dengan 20% elemen dalam array asli), kita masih dapat menyimpan analisis linier.
Kedua, dua panggilan rekursif memainkan peran yang berbeda secara fundamental. Tujuan dari panggilan rekursif pada saluran 5 adalah untuk menentukan elemen referensi yang baik untuk panggilan rekursif saat ini. Tujuan dari panggilan rekursif pada saluran 11 atau 13 adalah yang biasa - untuk secara rekursif menyelesaikan tugas yang lebih kecil yang tersisa oleh panggilan rekursif saat ini. Namun demikian, struktur rekursif dalam algoritma DSelect sepenuhnya mengikuti tradisi semua algoritma divide and conquer lainnya yang kami pelajari: setiap panggilan rekursif membuat sejumlah kecil panggilan rekursif berikutnya dengan subtugas yang lebih halus dan melakukan beberapa pekerjaan ekstra. Jika kami tidak khawatir bahwa algoritma seperti MergeSort atau QuickSort akan berjalan selamanya, maka kita tidak perlu khawatir tentang algoritma DSelect.
6.3.4. DSelect algoritma runtime
Algoritma DSelect bukan hanya program yang didefinisikan dengan baik yang menyelesaikan dalam jumlah waktu terbatas - ini berjalan dalam waktu linier, melakukan lebih banyak pekerjaan hanya pada faktor konstan daripada yang diperlukan untuk membaca data input.
Teorema 6.6 (waktu operasi algoritma DSelect). Untuk setiap larik input dengan panjang n ≥ 1, waktu berjalan algoritma DSelect adalah O (n).
Berbeda dengan run time dari algoritma RSelect, yang pada prinsipnya bisa tidak lebih dari Θ (n2), run time dari algoritma DSelect selalu sama dengan O (n). Namun demikian, dalam praktiknya, Anda harus lebih memilih RSelect ke algoritma DSelect, karena yang pertama bekerja di tempat yang sama, dan konstanta disembunyikan dalam waktu operasi rata-rata "O (n)" dalam Teorema 6.1 lebih kecil daripada konstanta yang tersembunyi di Teorema 6.6.
»Informasi lebih lanjut tentang buku ini dapat ditemukan di
situs web penerbit»
Isi»
KutipanUntuk diskon 20% Khabrozhiteley pada kupon -
AlgoritmaSetelah pembayaran versi kertas buku, versi elektronik buku dikirim melalui email.
PS: 7% dari biaya buku akan masuk ke terjemahan buku komputer baru, daftar buku yang diserahkan ke percetakan ada di
sini .