Muon katalisis dalam hal kimia kuantum. Bagian I: hidrogen biasa vs hidrogen muon

Mnogabukaff yang berpikir tentang kimia kuantum tentang prinsip katalisis muon: seberapa tepatnya muon menurunkan suhu plasma yang diinginkan. Dalam dua bagian.

Esensi dari bagian pertama diekspresikan dalam satu kalimat: muon lebih berat daripada elektron, sehingga lebih sulit untuk merenggutnya dari proton.

Tetapi mereka yang ingin melihat rumus, grafik, dan melihat esensi konseptual kimia kuantum sebagaimana diterapkan pada atom (kuasi) yang paling sederhana, diterima di bawah cat.

Bagian kedua tersedia di tautan ini .

Pendahuluan

Sudah bukan rahasia lagi bahwa konsumsi energi oleh umat manusia tumbuh setiap tahun: kita masing-masing memiliki lebih banyak gadget, kita harus bergerak di sana, dan kita sendiri tidak kurang. Karena itu, Kami terus-menerus berpikir, di mana mendapatkan lebih banyak energi, dan di mana menyimpan energi ini.

Salah satu alternatif yang memungkinkan untuk sumber energi utama saat ini (batubara, gas, pembangkit listrik tenaga air, dan tenaga nuklir) adalah fusi termonuklir (TS) . Sebenarnya, ini adalah saudara kembar yang baik dari energi nuklir jahat. Hal utama yang tidak perlu diingat tentang Tsar-Bomb adalah : alih-alih reaksi peluruhan nuklir, perpaduan inti cahaya menjadi yang lebih berat berfungsi sebagai sumber energi. Dan semuanya tampak baik-baik saja: semua sumber energi kita entah bagaimana muncul berkat TS, karena mengalir di bintang-bintang (termasuk bagian dalam Matahari) dan berfungsi sebagai sumber cahaya dan panas, yang dengannya semua reaksi fotosintesis terjadi, semua mengalir sungai dan angin berhembus. Tetapi juga berkat TS, kami memiliki banyak elemen yang lebih berat daripada helium (termasuk karbon = batubara, minyak, gas, dan uranium).
Reaksi sintesis putatif utama adalah reaksi fusi isotop hidrogen yang berbeda (protium $$${} _ {1} ^ {1} \ mathrm {H}$ deuterium $$${} _ {1} ^ {2} \ mathrm {H}$ dan tritium $$${} _ {1} ^ {3} \ mathrm {H}$ )

Masalahnya adalah bahwa untuk memulai kendaraan dalam mode mandiri Anda membutuhkan suhu yang sangat tinggi. Tidak ada masalah dengan bintang-bintang, tetapi dalam kondisi terestrial, persyaratan seperti itu masih menjadi hambatan bagi arus yang mengalir dari fusi termonuklir ramah lingkungan di setiap outlet.

Salah satu cara untuk menurunkan suhu adalah katalisis muon .
Vicki memberi tahu kita bahwa muon ( $$$\ mu ^ -$ ) Merupakan klon elektron berat yang tidak stabil ( $$$e ^ -$ ): ini 207 kali lebih berat dari sebuah elektron, dan hanya hidup 2,2 mikrodetik. Namun, diasumsikan bahwa penambahan partikel tersebut ke sistem di mana TS terjadi, akan dapat menurunkan suhu plasma minimum yang diperlukan untuk fusi inti baru. Dan karena muon dapat terbentuk selama beberapa reaksi sintesis, alih-alih partikel yang membusuk, partikel baru akan muncul yang akan terus terlibat dalam alkimia untuk membakar hidrogen dan elemen lain dengan pembentukan yang lebih berat.

Dalam perbedaan antara bentuk-bentuk hidrogen yang biasa dan yang di mana elektron digantikan oleh muon dan seluruh esensi katalisis muon dibahas. Dan untuk melihat ini, kita perlu beralih ke kimia kuantum dan konsepnya, yang akan kita lakukan.

Pada bagian ini, kita akan fokus pada perbedaan dalam atom hidrogen ( $$$\ mathrm {H ^ \ cdot = p ^ + e ^ -}$ ) dari mitranya muon ( $$$\ mathrm {p} ^ + \ mu ^ -$ ), di mana elektron digantikan oleh muon.

Terbang di atas sarang proton ...

Beberapa kata yang umum

Atom hidrogen. Semua orang mendiskusikannya dan berlangsung di sekolah dalam kelas fisika dan kimia, jadi kita akan membahas bagaimana mengganti elektron dengan muon akan memengaruhi sifatnya (energi dan jenis orbital).
Kami mempertimbangkan partikel-partikel ini dari dua posisi umum:

• sesat (yang disebut mekanika kuantum tua),
• dan dari sudut pandang quantummech normal.

Pertimbangan pertama tersedia untuk anak sekolah, yang kedua akan membutuhkan pengetahuan yang lebih dalam tentang matematika yang lebih tinggi .

Bohr mengorbit

Faktanya, mekanika kuantum lama adalah upaya untuk mengadaptasi mekanika klasik untuk menggambarkan sistem yang tidak mematuhinya. Terlepas dari kenyataan bahwa untuk uraian lengkap, pendekatan ini sangat cacat (yang akan kita bahas di bagian selanjutnya), ini penting dan menarik, dan pada saat yang sama sangat sederhana.

• Pertama, melalui mekanika kuantum lama fisikawan berhasil mengendus apa yang salah dengan sistem kuantum, oleh karena itu, dari sudut pandang historis, langkah ini diperlukan dan penting untuk mengubah paradigma fisika.
• Kedua, solusi Bohr untuk masalah atom atom mirip hidrogen yang terdiri dari dua partikel bermuatan positif dan negatif dapat menjelaskan pengamatan eksperimental dan menghubungkan bersama seluruh kebun binatang seri yang diamati dalam spektrum hidrogen. Versi merusak dari keputusan ini, yang membawa Bohr Nobel 1922, kami akan pertimbangkan di sini.

Tetapi untuk menyelesaikan masalah, kita harus ingat bagaimana kita menggambarkan gerakan partikel dalam kasus klasik. Ini adalah program sekolah dalam fisika, tetapi jika seseorang lupa, Anda dapat menyegarkan ingatan Anda di sini:




Mari kita beralih ke tugas. Jadi, kami memiliki dua partikel bermuatan berlawanan yang tertarik satu sama lain menurut hukum Coulomb, yaitu energi potensial tarik adalah

$$

$$V (R) = \ overbrace {\ frac {1} {4 \ pi \ varepsilon_0}} ^ {k} \ frac {q_1 q_2} {R} = k \ frac {q_1 q_2} {R}$$

di mana R adalah jarak antara partikel, $$$q_i$ - Muatan dalam hal atom hidrogen dan partikel $$$\ mathrm {p} ^ + \ mu ^ -$ mereka sama $$$+ e \ sekitar +1.6 \ kali 10 ^ {- 19}$ CL untuk proton dan $$$-e$ untuk elektron dan muon, dan $\ varepsilon_0$ - konstanta listrik . Karena muatannya berseberangan, energi potensial berkurang dengan menurunnya jarak antar partikel (mis., Selama pendekatan), yang berarti bahwa proton dan elektron / muon saling tertarik.

Situasi ini ditunjukkan pada gambar di atas. Tetapi di suatu tempat kita melihat sistem yang sama, kan? Sebenarnya, pada salah satu pasangan ini kita hidup: Matahari + Bumi atau Bumi + Bulan, atau Bumi + ISS - ini juga dua partikel yang tertarik oleh potensi serupa yang diungkapkan oleh hukum Newton:

$$

$$V (R) = -G \ frac {m_1 m_2} {R}$$

di mana G adalah konstanta gravitasi, dan $$$m_i$ - massa.

Proton 1836 kali lebih berat dari elektron, dan karena muon 207 kali lebih berat dari elektron, proton hampir 9 kali lebih berat daripada muon. Dalam kedua kasus, kita memiliki sistem "partikel berat + partikel cahaya", jadi kita mengambil perkiraan di mana elektron / muon berputar di sekitar proton. Tentu saja, ketepatan asumsi ini dalam kasus $$$\ mathrm {p} ^ + \ mu ^ -$ akan secara signifikan lebih rendah daripada atom hidrogen, tetapi untuk ilustrasi itu cukup cocok. Dalam kasus Matahari + Bumi, Bumi + ISS biasanya menggunakan perkiraan yang sama.

Kami tertarik pada sistem yang stabil di mana tidak ada yang jatuh di mana pun, karena atom hidrogen, jika tidak tersentuh, ada untuk waktu yang sangat lama.

Kita tahu gerakan seperti itu dalam kasus semua analog dari tata surya, tetapi bahkan jelas untuk pasangan ISS Bumi: ini adalah orbit stabil di mana stasiun bergerak mengelilingi Bumi dengan kecepatan yang cukup untuk tidak jatuh. Kecepatan ini disebut kecepatan kosmik pertama , yaitu kita akan membutuhkan kecepatan kosmik pertama untuk atom hidrogen / padanan muonnya. Dan mudah menemukannya dengan formula sekolah (lihat gambar di atas).

Ketika bergerak dalam orbit melingkar dengan jari-jari R (pada gambar ditunjukkan sebagai $$$a_0$ , dan segera kita sampai di sini) Anda harus memiliki kecepatan $$$v$ . Orang dapat membayangkan bahwa pada setiap saat dua gaya yang bekerja pada partikel yang terbang dalam lingkaran tegak lurus terhadap vektor kecepatan:

• Gaya gravitasi Coulomb diarahkan ke pusat, yang sesuai dengan definisi gaya $$$F = - \ frac {dV} {dR}$ sama dengan
  

  $$

  $$F_ \ text {K} = -k \ frac {e ^ 2} {R ^ 2}$$
  
  
• gaya sentrifugal (palsu) melawannya , yang mencoba meningkatkan jari-jari orbit R , ungkapan untuk itu memiliki bentuk
  

  $$

  $$F_ \ text {q} = \ frac {mv ^ 2} {R}$$
  
  di mana m adalah massa elektron / muon (satelit proton alami).
  

Kondisi bahwa partikel cahaya tidak menabrak yang berat adalah bahwa jumlah gaya-gaya ini tegak lurus terhadap arah gerakan partikel harus nol ( $$$F_ \ mathrm {K} + F_ \ mathrm {q} = 0$ ), yang berarti kita mendapatkan persamaannya

$$

$$\ frac {mv ^ 2} {R} = k \ frac {e ^ 2} {R ^ 2}$$

dari mana kita mendapatkan kecepatan yang diperlukan untuk menerbangkan elektron / muon dengan massa m pada jari-jari orbit R , agar tidak menabrak proton:

$$

$${v} = \ sqrt {k \ frac {e ^ 2} {mR}}$$

Dan semuanya akan terluka jika elektron / muon tidak bermuatan, dan partikel bermuatan memancarkan gelombang elektromagnetik ketika bergerak dalam lingkaran (ini disebut gesekan radiasi) , yang akan membuat sistem seperti itu tidak stabil: elektron / muon akan memancarkan cahaya selama rotasi, sebagai hasilnya, ia kehilangan energi dan mengurangi jari-jari orbitnya, dan pada akhirnya akan jatuh pada proton, dan akan ada binatang berbulu putih kecil untuk semuanya. Tetapi, jelas, ini tidak terjadi, yang berarti bahwa sesuatu harus secara radikal berbeda dalam perilaku partikel kecil seperti elektron / muon.

Sebenarnya, Niels Bohr juga mengusulkan hipotesis yang sangat bodoh (pada waktu itu). Dia mengakui bahwa ada orbit dengan jari-jari tertentu, di mana atom hidrogen tidak memancarkan apa pun. Dan sekarang pertanyaannya adalah bagaimana menemukan orbit ini. Untuk kesederhanaan, kami akan menggunakan pencapaian lebih lambat dari yang tersedia untuk Bohr: ungkapan untuk panjang gelombang de Broglie :

$$

$$\ lambda = \ frac {h} {p} = \ frac {h} {mv}$$

Diasumsikan bahwa materi (partikel) juga memiliki sifat gelombang, dan mereka dapat dikaitkan dengan panjang gelombang tertentu, yang diberikan oleh rumus de Broglie. Kemudian, agar gerakan dalam lingkaran menjadi diam pada waktunya (menjadi gelombang berdiri), diperlukan panjang orbit ( $$$L = 2 \ pi R$ ) cocok dengan bilangan bulat bilangan.

Maka gerakan gelombang elektron / muon dapat direpresentasikan seperti ini ( diambil dari Wiki ):

Dalam bahasa formula, ini dinyatakan sebagai:

$$

$$2 \ pi R = n \ lambda = n \ frac {h} {mv}$$

Mengganti di sini kecepatan proton kosmik pertama yang diperoleh di atas, kita memperoleh persamaan $$$2 \ pi R = \ frac {nh} {m} \ sqrt {\ frac {mR} {ke ^ 2}}$ . Setelah mengkuadratkan kedua sisi, kita memperoleh ekspresi untuk jari-jari orbit elektron / muon ke-n:

$$

$$R_n = n ^ 2 \ kiri (\ overbrace {\ frac {h} {2 \ pi}} ^ {\ hbar} \ kanan) ^ 2 \ cdot \ frac {1} {mk e ^ 2} = \ frac { n ^ 2 \ hbar ^ 2} {mk e ^ 2}$$

Di sini $$$n = 1,2,3, \ ldots$ (kami tidak memiliki batasan jumlah gelombang yang akan diletakkan), dan $$$\ hbar$ - ini yang disebut mengurangi konstanta Planck. Semakin banyak gelombang yang kita tumpuk, semakin besar radius orbitnya. Dengan jari-jari minimum ( n = 1) dalam kasus elektron (mis., M sama dengan massa elektron m _e ), jari-jari ini disebut jari-jari Bohr, seperti kata K.O, untuk menghormati Niels Bohr, dan dinotasikan sebagai ₀ (lihat Gambar di atas):

$$

$$a_0 = R_0 = \ frac {\ hbar ^ 2} {m_ \ mathrm {e} ke ^ 2}$$

Substitusi angka ( ħ = 1,054 × 10 ^–34 J · s, m _e = 9,109 × 10 ^-31 kg, k = 8,99 × 10 ⁹ N · m ² · C ⁻² dan e = 601.602 × 10 ⁻¹⁹ C) memberikan nilai a ₀ = 5,29 × 10 ⁻¹¹ m atau 0,529 angstrom (Å).


Dalam proses perhitungan, kami secara sepintas memperkenalkan entitas baru: angka $$$n = 1,2,3, \ ldots$ yang menentukan jumlah gelombang dan $$$\ Rightarrow$ jari-jari orbit, dan bahkan kecepatan elektron di orbit. Angka ini diketahui oleh semua orang dari sekolah: ini adalah nomor kuantum paling penting dari atom yang mirip hidrogen. Kami akan membicarakan hal ini secara lebih rinci di bagian selanjutnya, tetapi untuk sekarang Anda dapat mencoba menemukan energi dari masing-masing level.

Seperti yang kita pahami, energi dari sistem tertutup (dan tidak ada keraguan bahwa atom mirip hidrogen kita demikian) terdiri dari dua bagian:

• dari energi kinetik $$$T = \ frac {mv ^ 2} {2}$ ,
• dan potensi, yang dalam kasus kami diberikan oleh hukum Coulomb $$$V = \ frac {ke ^ 2} {R}$ .

Kami mengganti kecepatan dan jari-jari orbit di dalamnya untuk bilangan pokok yang dipilih n . Kami sudah menuliskan radiusnya, tetapi kecepatannya akan terlihat seperti $$$v_n ^ 2 = \ frac {k e ^ 2} {m R_n} = \ frac {k ^ 2 e ^ 4} {n ^ 2 \ hbar ^ 2}$ .

Lalu $$$T_n = \ frac {m v_n ^ 2} {2} = \ frac {m} {2} = \ frac {m k ^ 2 e ^ 4} {2 n ^ 2 \ hbar ^ 2}$ . Dengan potensi, semuanya lebih sederhana: $$$V_n = - \ frac {ke ^ 2} {R_n} = - \ frac {m k ^ 2 e ^ 4} {n ^ 2 \ hbar ^ 2}$ . Ringkasnya kontribusi ini, kami memperoleh energi total dari atom mirip-hidrogen:

$$

$$E_n = T_n + V_n = - \ frac {m k ^ 2 e ^ 4} {2 n ^ 2 \ hbar ^ 2}$$

Dan formula ini memainkan peran besar dalam membuktikan kebenaran mekanika kuantum, karena tumpukan garis spektral (Lyman, Balmer, Paschen, dll.) Diamati dalam spektrum atom hidrogen. Dan dengan satu formula dan model sederhana, mereka semua berhasil dijelaskan sekaligus, yang merupakan argumen yang sangat meyakinkan untuk mengakui ide-ide Bohr.

Setelah memeras semua jus dari model paling sederhana ini, kita dapat melanjutkan ke pertimbangan yang benar dari masalah dari sudut pandang mekanika kuantum yang jujur.

Orbit atom mirip hidrogen

Yang kedua, hal yang lebih penting adalah apa itu mekanika kuantum dan cara kerjanya. Ini bisa diingat dari berbagai sumber. Saya merekomendasikan:

• tidak jauh, sebuah artikel dari Habr: Book “Mekanika kuantum. Teoritis minimum ” (sepotong buku dengan nama yang sama oleh Leonard Sasskind dan Art Friedman ),
• buku yang luar biasa "Bagaimana memahami mekanika kuantum" dari guru MFTIshnogo MG Ivanova (tersedia untuk diunduh dari tautan),
• pada forum dxdy di Terpilih, ada banyak posting yang menjelaskan esensi dari kuantumme dengan baik ,
• Ulasan dan artikel sejarah yang cukup cocok tentang Lurke
• Ya, semua sampah juga ditemukan di Internet.

  manual jaringan pada kimia kuantum dari VK .
  

Namun, ada juga hal-hal yang perlu ditekan di sini:


Untuk menemukan bagaimana elektron / muon bergerak dalam medan listrik Coulomb yang dibuat oleh proton, seseorang harus menyelesaikan persamaan dasar mekanika kuantum: persamaan Schrödinger. Karena sistem yang dipertimbangkan adalah stasioner (tidak berubah seiring waktu), itu sudah cukup untuk menyelesaikan versi yang disederhanakan: persamaan Schrödinger stasioner, yang memiliki bentuk

$$

$$\ underbrace {(\ overbrace {- \ frac {\ hbar ^ 2} {2m} \ cdot \ left (\ frac {\ partial ^ 2} {\ partial x ^ 2} + \ frac {\ partial ^ 2} { \ partial y ^ 2} + \ frac {\ partial ^ 2} {\ partial z ^ 2} \ kanan)} ^ {\ hat {T}} + \ overbrace {- \ frac {ke ^ 2} {R}} ^ {\ hat {V}})} _ {\ hat {H}} \ psi = E \ psi$$

Persamaan ini adalah persamaan diferensial parsial orde kedua, dan di dalamnya kita secara bersamaan mencari fungsi gelombang $$$\ psi (x, y, z)$ menggambarkan keadaan spesifik sistem dan menunjukkan "pengolesan" partikel negatif dalam ruang di sekitar proton, dan energi dari keadaan ini E. Ilmu sihir memutuskan itu dapat ditemukan lebih atau kurang di mana-mana .


Tetapi hal yang lebih sederhana: siapa pun yang terbiasa dengan persamaan diferensial dapat menemukan solusi untuk keadaan dasar atom mirip hidrogen. Agar tidak membuat orang lain takut, bagian ini dihapus di spoiler:


Hasil dari penyelesaian persamaan Schrödinger adalah seperangkat orbital, yang dideskripsikan menggunakan tiga bilangan bulat n , l dan m , yang disebut "bilangan kuantum". Ketergantungan pada energi orbital ini $$$(n, l, m)$ diberikan di bawah ini (dan steren dari sumber keren dalam kimia ):

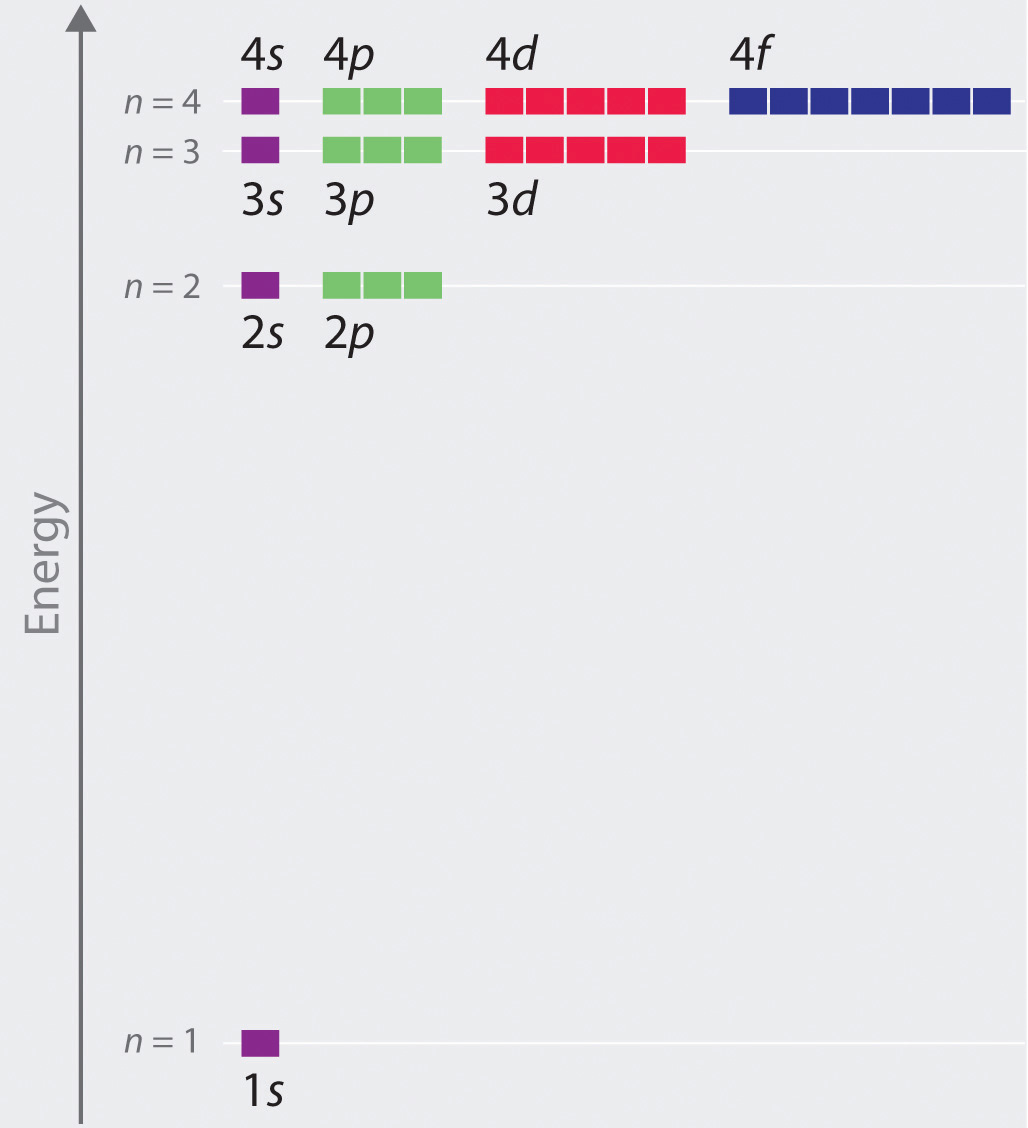
1. Dengan angka pertama, n = 1,2,3, ... kita sudah bertemu. Inilah yang disebut bilangan kuantum utama. Ini menentukan energi tingkat, serta ukuran orbit Bohr. (.. ) «». , / , , — , , , . n =1 n =2 ( ):
   
   
   : , n . , .
2. l , , . n , n ( $$$l = 0, 1,2, \ldots, n$ ). , . , , . , ( $$$\psi=0$ ), , . - ( ):
   
   
   
   «» . , .
   
   
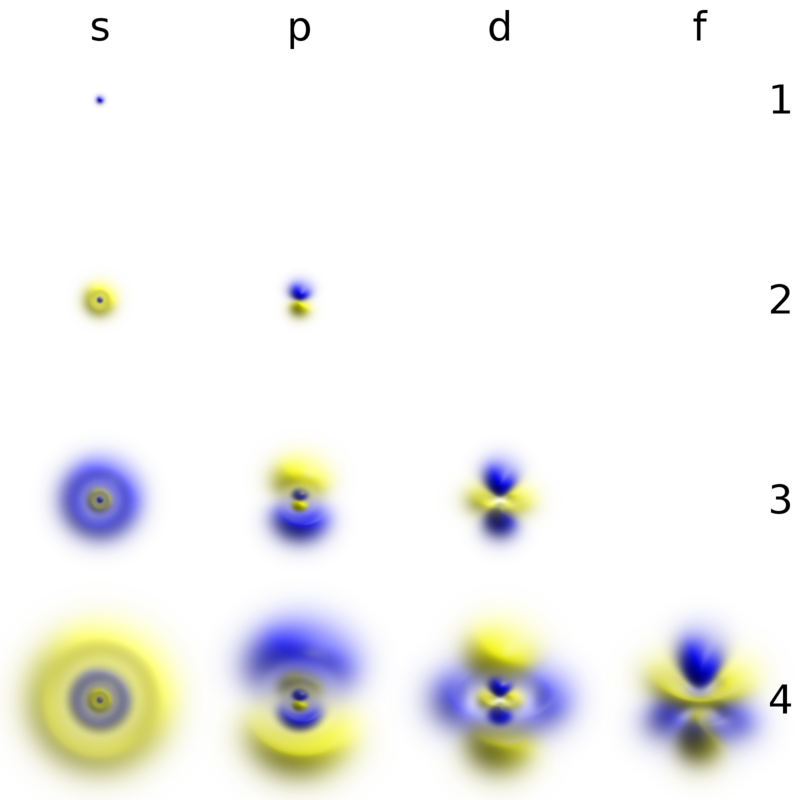
   • $$$l=0$ , , , . s-.
   • ( $$$l=1$ ) p-.
   • 4- $$$l=2$ , d-. .
   • 6- ( $$$l=3$ ) f-.
   • 8- ( $$$l=4$ ) g-.
   • 10- ( $$$l=5$ ) h-.
   • Dll dll.
   
   , ( n ) , . : , .
   
3. , m , . . 2l+1 : $$$m = -l, -l+1, \ldots, 0 , \ldots , l-1, l$ .

Apa yang kita dapatkan sebagai hasilnya: energi dalam kasus kuantum ternyata sama dengan energi Bohr, tetapi jumlah keadaan yang memungkinkan untuk n yang diberikan ternyata juga merupakan jumlah yang terbatas. Dan jumlah ini tumbuh dengan meningkatnya energi orbital. Tanpa diduga, tetapi setuju dengan eksperimen.

Jadi apa perbedaan antara atom hidrogen ( $$H ⋅ = p + e - ) dari mitranya muon ($\mathrm{H}^\cdot = \mathrm{p^+ e^-}$$$p + μ - )?$\mathrm{p}^+ \mu^-$

Sekarang kita menerapkan formula yang diperoleh untuk memahami apa yang sebenarnya berubah ketika sebuah elektron digantikan oleh muon dalam atom hidrogen.

• Energi keadaan dasar (mis., Energi minimum, paling stabil, dari mana tidak ada tempat), dengan bilangan kuantum utama n = 1. Itu diberikan oleh formula
  

  $$

  $$E_1 = - \frac{m k^2 e^4}{2 \underbrace{n^2}_{1^2} \hbar^2} = - \frac{m k^2 e^4}{2 \hbar^2}$$
  
  Ketika sebuah elektron transfer ke muon, hanya massa ( $$$m_{\mu} \approx 207 m_\mathrm{e}$ , — , — ). , 207 : $$$E_1(\mathrm{p}^+\mu^-) = 207 E_1(\mathrm{H}^\cdot)$
  
• . //, . $$$\mathrm{A \rightarrow A^+ + e^-}$ , A — . , $$$\mathrm{A \rightarrow A^+ + \mu^-}$ . . $$$E=0$ . $$$E_n = - \frac{m k^2 e^4}{2{n^2}\hbar^2}$ $$$n \rightarrow + \infty$ . Yaitu , , / , , - (. ).
  
  , ( $$$E>0$ , ).
  
  , (IP) +/ :
  

  $$

  $$\mathrm{IP} = \underbrace{0}_{\text{ }} - \underbrace{E_1}_{\text{ }} = -E_1$$
  
  , + 207 , , .. «» , .
  
• , «». , , (1s-)
  

  $$

  $$\psi_{1s}(R) = c\cdot \exp\left(-\frac{R}{R_1} \right)$$
  
  $$$R_1 = \frac{\overbrace{n^2}^{1^2} \hbar^2 }{mk e^2} = \frac{ \hbar^2 }{mk e^2}$ , semakin cepat fungsi gelombang berkurang dengan jarak dari proton, dan semakin kecil "ukuran" -nya, yaitu. lokalisasi partikel bermuatan negatif. Ketika berpindah dari satu elektron ke muon, jari-jari R1 ini berkurang dengan faktor 207, oleh karena itu, ternyata muon itu lebih dekat pada proton daripada elektron. Dan oleh karena itu, lebih sulit untuk melepaskannya, karena ionisasi pada dasarnya adalah transisi ke orbit yang jauh, mis. muon harus lebih dari sekadar elektron untuk melarikan diri dari proton.
  

Secara konseptual, semua kesimpulan kami dari formula adalah sangat sederhana: untuk memecahkan masalah $$$\ mathrm {H ^ \ cdot}$ dan $$$\ mathrm {p} ^ + \ mu ^ -$ terlihat sama, tetapi karena fakta bahwa muon lebih berat, ia lebih menempel pada proton, dan lebih sulit baginya untuk melarikan diri dari itu.

Jelas kan? Tetapi dengan formula itu masih lebih jelas.

Apa yang akan terjadi selanjutnya?

Teks ini hanyalah persiapan untuk bagian selanjutnya.

Di dalamnya, kita akan langsung membahas mekanisme yang diusulkan untuk menurunkan suhu minimum fusi.

Sistem unit atom PS

Akhirnya, kami membahas hal yang akan sangat menyederhanakan kami semua formula yang ditulis di atas. Dalam tugas yang berbeda (bahkan sekolah), pemilihan satuan ukuran dapat sangat memudahkan kehidupan. Dan dalam kasus mekanika kuantum, ada juga sistem unit yang sangat nyaman. Inilah yang disebut sistem satuan atom . Itu milik kelas unit alami, yang pada dasarnya kebalikan dari unit antroposentris ( SI , GHS ), di mana jumlah yang dapat segera dibayangkan seseorang digunakan sebagai potongan referensi. Sebagai contoh, di SI, satuan panjangnya adalah satu meter (kira-kira panjang lengan / kaki orang dewasa), massa - satu kilogram (kira-kira massa bir dalam lingkaran di Oktoberfest), semua ini kita amati dalam kehidupan sehari-hari.

Namun, sistem satuan alamiah sebagai dasar sesuatu yang menyederhanakan formula dalam bidang pengetahuan yang sesuai. Dan dalam kasus unit atom:

• pertama-tama, konstanta Planck di mana-mana diasumsikan bersatu ( $$$\ hbar = 1$ ),
• satuan massa adalah massa elektron $$$m_ \ mathrm {e} \ sekitar 9,1 \ kali 10 ^ {- 31}$ kg
• satuan muatan adalah muatan proton (atau, ekuivalen, modulus muatan elektron) $$$e = 1,6 \ kali 10 ^ {- 19}$ Kl
• Nah, pada saat yang sama, konstanta listrik diambil sebagai unit $$$k = \ frac {1} {4 \ pi \ varepsilon_0}$ , karena itu hukum Coulomb mengambil bentuk $$$V (R) = \ frac {q_1 q_2} {R}$ .

Dalam hal ini, jari-jari Bohr dari keadaan dasar untuk atom hidrogen menjadi satuan panjang $$$a_0 = R_1 = \ frac {\ hbar ^ 2} {m_ \ mathrm {e} k e ^ 2} = 1$ (seingat kita, ini sekitar 0,5 Å). Unit energi menjadi nilai yang disebut Hartree (untuk menghormati sudut D dari Hartree ), yang dilambangkan $$$E_ \ mathrm {h} = \ frac {m_ \ mathrm {e} k ^ 2 e ^ 4} {\ hbar ^ 2} = 1$ . Terlihat bahwa energi level 1s hidrogen dalam satuan atom adalah 0,5 Hartree.

Pada bagian selanjutnya, kita akan secara aktif duduk di unit-unit ini.