Memahami Q-learning, masalah "Berjalan di atas batu"

Halo, Habr! Saya membawa perhatian Anda pada terjemahan dari artikel "Memahami Q-Learning, masalah the Cliff Walking" oleh Lucas Vazquez .

Dalam posting terakhir, kami menyajikan masalah "Berjalan di atas batu" dan menetapkan algoritma yang mengerikan yang tidak masuk akal. Kali ini kami akan mengungkapkan rahasia kotak abu-abu ini dan melihat bahwa itu tidak begitu menakutkan sama sekali.

Ringkasan

Kami menyimpulkan bahwa dengan memaksimalkan jumlah imbalan di masa depan, kami juga menemukan jalur tercepat ke sasaran, jadi sasaran kami sekarang adalah menemukan cara untuk melakukan ini!

Pengantar Q-Learning

• Mari kita mulai dengan membangun tabel yang mengukur seberapa baik tindakan tertentu akan tampil di negara bagian mana pun (kita bisa mengukurnya dengan nilai skalar sederhana, jadi semakin besar nilainya, semakin baik tindakan)
• Tabel ini akan memiliki satu baris untuk setiap negara bagian dan satu kolom untuk setiap tindakan. Di dunia kita, grid memiliki 48 (4 oleh Y oleh 12 oleh X) menyatakan dan 4 tindakan diizinkan (atas, bawah, kiri, kanan), sehingga tabel akan menjadi 48 x 4.
• Nilai yang disimpan dalam tabel ini disebut "nilai-Q."
• Ini adalah perkiraan jumlah hadiah di masa depan. Dengan kata lain, mereka memperkirakan berapa banyak hadiah yang bisa kita dapatkan sebelum akhir pertandingan, dalam keadaan S dan melakukan aksi A.
• Kami menginisialisasi tabel dengan nilai acak (atau konstanta, misalnya, semua nol).

"Q-table" yang optimal memiliki nilai-nilai yang memungkinkan kita untuk mengambil tindakan terbaik di setiap negara bagian, memberikan kita cara terbaik untuk menang pada akhirnya. Masalahnya terpecahkan, tepuk tangan, Robot Lords :).

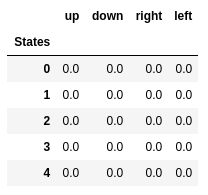Nilai-Q dari lima negara bagian pertama.

Q-learning

• Q-learning adalah algoritma yang “mempelajari” nilai-nilai ini.
• Di setiap langkah kami mendapatkan informasi lebih lanjut tentang dunia.
• Informasi ini digunakan untuk memperbarui nilai-nilai dalam tabel.

Sebagai contoh, anggaplah kita satu langkah menjauh dari target (kuadrat [2, 11]), dan jika kita memutuskan untuk turun, kita mendapatkan hadiah 0 bukannya -1.
Kita dapat menggunakan informasi ini untuk memperbarui nilai pasangan tindakan-negara di tabel kita, dan saat berikutnya kita mengunjunginya, kita akan tahu bahwa bergerak ke bawah memberi kita hadiah 0.

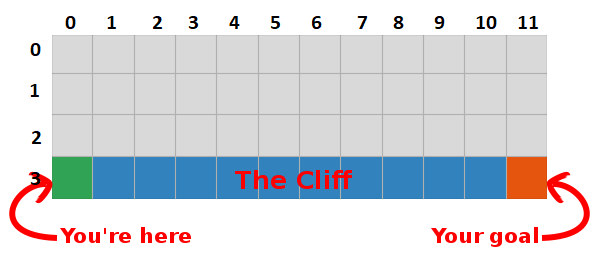
Sekarang kami dapat menyebarkan informasi ini lebih jauh! Karena kita sekarang tahu jalan menuju tujuan dari kuadrat [2, 11], tindakan apa pun yang membawa kita ke alun-alun [2, 11] juga akan baik, oleh karena itu kita memperbarui nilai-Q dari kuadrat, yang mengarahkan kita ke [2, 11] lebih dekat ke 0.

Dan itu, hadirin sekalian, adalah inti dari pembelajaran Q!

Harap perhatikan bahwa setiap kali kami mencapai tujuan, kami meningkatkan "peta" kami tentang cara mencapai tujuan dengan satu kotak, jadi setelah jumlah iterasi yang memadai, kami akan memiliki peta lengkap yang akan menunjukkan kepada kami cara mencapai tujuan dari setiap negara.

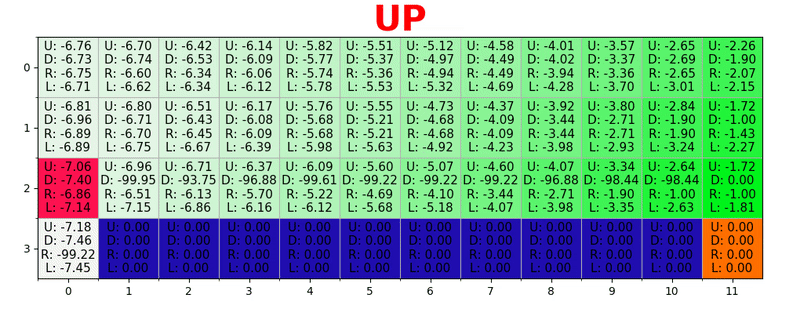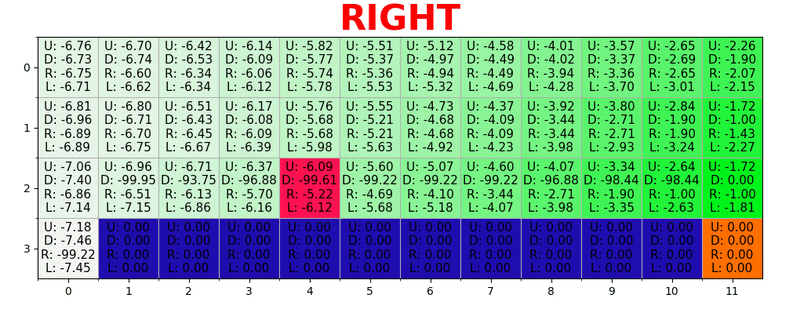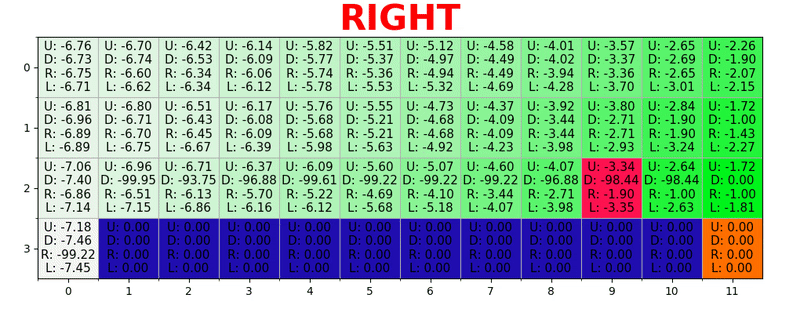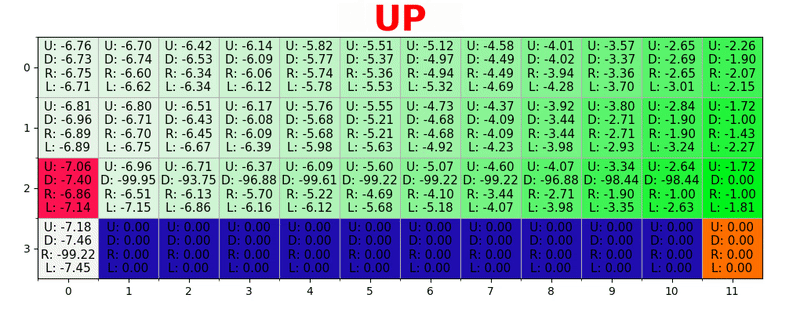Sebuah jalur dihasilkan dengan mengambil tindakan terbaik di setiap negara bagian. Kunci hijau mewakili makna tindakan yang lebih baik, kunci yang lebih jenuh mewakili nilai yang lebih tinggi. Teks mewakili nilai untuk setiap tindakan (atas, bawah, kanan, kiri).

Persamaan Bellman

Sebelum kita berbicara tentang kode, mari kita bicara tentang matematika: konsep dasar belajar-Q, persamaan Bellman.

• Pertama mari kita lupakan γ dalam persamaan ini
• Persamaan menyatakan bahwa nilai Q untuk pasangan tindakan-negara tertentu harus menjadi hadiah yang diterima saat transisi ke negara baru (dengan melakukan tindakan ini), ditambahkan ke nilai tindakan terbaik di negara berikutnya.

Dengan kata lain, kami menyebarkan informasi tentang nilai-nilai tindakan satu langkah pada satu waktu!

Tetapi kita dapat memutuskan bahwa menerima hadiah saat ini lebih berharga daripada menerima hadiah di masa depan, dan oleh karena itu kita memiliki γ, angka dari 0 hingga 1 (biasanya dari 0,9 menjadi 0,99) yang dikalikan dengan hadiah di masa depan, mendiskontokan hadiah di masa depan.

Jadi, mengingat γ = 0,9 dan menerapkan ini ke beberapa negara di dunia kita (kisi), kita memiliki:

Kita dapat membandingkan nilai-nilai ini dengan yang di atas dalam GIF dan melihat bahwa semuanya sama.

Implementasi

Sekarang setelah kita memiliki pemahaman intuitif tentang cara kerja pembelajaran-Q, kita dapat mulai berpikir tentang mengimplementasikan semua ini, dan kita akan menggunakan kode semu belajar-Q dari buku Sutton sebagai panduan.

Kode semu dari buku Sutton.

Kode:

# Initialize Q arbitrarily, in this case a table full of zeros q_values = np.zeros((num_states, num_actions)) # Iterate over 500 episodes for _ in range(500): state = env.reset() done = False # While episode is not over while not done: # Choose action action = egreedy_policy(q_values, state, epsilon=0.1) # Do the action next_state, reward, done = env.step(action) # Update q_values td_target = reward + gamma * np.max(q_values[next_state]) td_error = td_target - q_values[state][action] q_values[state][action] += learning_rate * td_error # Update state state = next_state 

• Pertama, kita mengatakan: "Untuk semua negara dan tindakan, kita menginisialisasi Q (s, a) secara sewenang-wenang", ini berarti bahwa kita dapat membuat tabel nilai-Q dengan nilai apa pun yang kita suka, mereka dapat acak, mereka dapat menjadi segala bentuk yang permanen tidak masalah. Kita melihat bahwa pada baris 2 kita membuat tabel yang penuh dengan nol.

Kami juga mengatakan: "Nilai Q untuk kondisi akhir adalah nol", kami tidak dapat mengambil tindakan apa pun di kondisi akhir, oleh karena itu kami menganggap nilai untuk semua tindakan di negara ini menjadi nol.

• Untuk setiap episode, kita harus "menginisialisasi S", ini hanya cara mewah untuk mengatakan "restart game", dalam kasus kami itu berarti menempatkan pemain di posisi awal; di dunia kita ada metode yang melakukan hal itu, dan kita menyebutnya jalur 6.
• Untuk setiap langkah waktu (setiap kali kita perlu bertindak), kita harus memilih tindakan yang diperoleh dari Q.

Ingat, saya berkata, “apakah kita mengambil tindakan yang paling berharga di setiap kondisi?

Ketika kami melakukan ini, kami menggunakan nilai-Q kami untuk membuat kebijakan; dalam hal ini akan menjadi kebijakan serakah, karena kami selalu mengambil tindakan yang, menurut pendapat kami, adalah yang terbaik di setiap negara bagian, oleh karena itu dikatakan bahwa kami bertindak rakus.

Sampah

Tetapi ada masalah dengan pendekatan ini: bayangkan bahwa kita berada di labirin yang memiliki dua hadiah, satu adalah +1, dan yang lainnya adalah +100 (dan setiap kali kita menemukan salah satu dari mereka, permainan berakhir). Karena kami selalu mengambil tindakan yang kami anggap sebagai yang terbaik, kami akan terjebak dengan penghargaan pertama yang ditemukan, selalu kembali ke sana, oleh karena itu, jika kami pertama kali mengenali penghargaan +1, maka kami akan kehilangan penghargaan +100 besar.

Solusi

Kita perlu memastikan bahwa kita telah mempelajari dunia kita dengan cukup (ini adalah tugas yang sangat sulit). Di sinilah ε berperan. ε dalam algoritma serakah berarti bahwa kita harus bertindak dengan penuh semangat, TETAPI untuk melakukan tindakan acak sebagai persentase dari ε dari waktu ke waktu, jadi dengan jumlah upaya yang tak terbatas, kita harus memeriksa semua status.

Tindakan dipilih sesuai dengan strategi ini di baris 12, dengan epsilon = 0,1, yang berarti bahwa kita sedang melakukan penelitian di dunia 10% dari waktu. Implementasi kebijakan adalah sebagai berikut:

 def egreedy_policy(q_values, state, epsilon=0.1): # Get a random number from a uniform distribution between 0 and 1, # if the number is lower than epsilon choose a random action if np.random.random() < epsilon: return np.random.choice(4) # Else choose the action with the highest value else: return np.argmax(q_values[state]) 

Pada baris 14 dalam daftar pertama, kami memanggil metode langkah untuk melakukan tindakan, dunia mengembalikan kita keadaan berikutnya, hadiah dan informasi tentang akhir permainan.

Kembali ke matematika:

Kami memiliki persamaan panjang, mari kita pikirkan:

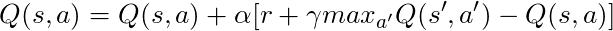
Jika kita mengambil α = 1:

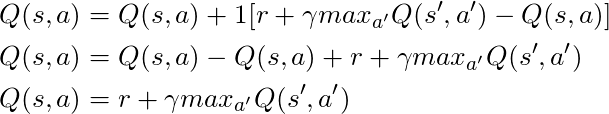
Yang persis cocok dengan persamaan Bellman, yang kami lihat beberapa paragraf yang lalu! Jadi kita sudah tahu bahwa ini adalah garis yang bertanggung jawab untuk menyebarkan informasi tentang nilai-nilai negara.

Tetapi biasanya α (kebanyakan dikenal sebagai kecepatan belajar) jauh lebih sedikit dari 1, tujuan utamanya adalah untuk menghindari perubahan besar dalam satu pembaruan, jadi alih-alih terbang ke tujuan, kami perlahan mendekatinya. Dalam pendekatan tabular kami, pengaturan α = 1 tidak menyebabkan masalah, tetapi ketika bekerja dengan jaringan saraf (lebih lanjut tentang ini dalam artikel berikut), semuanya dapat dengan mudah lepas kendali.

Melihat kode, kita melihat bahwa pada baris 16 dalam daftar pertama yang kita tentukan td_target, ini adalah nilai yang harus kita dekati, tetapi alih-alih langsung menuju nilai ini di baris 17, kita menghitung td_error, kita akan menggunakan nilai ini dalam kombinasi dengan kecepatan belajar perlahan-lahan bergerak menuju tujuan.

Ingatlah bahwa persamaan ini adalah entitas Q-Learning.

Sekarang kita hanya perlu memperbarui keadaan kita, dan semuanya sudah siap, ini adalah baris 20. Kita ulangi proses ini sampai kita mencapai akhir episode, sekarat di batu atau mencapai tujuan.

Kesimpulan

Sekarang kita secara intuitif memahami dan tahu cara menyandikan Q-Learning (setidaknya versi tabular), pastikan untuk memeriksa semua kode yang digunakan untuk posting ini, tersedia di GitHub .

Visualisasi tes proses pembelajaran:

Harap dicatat bahwa semua tindakan dimulai dengan nilai yang melebihi nilai akhirnya, ini adalah trik untuk merangsang eksplorasi dunia.