Kami telah membahas
mesin pengindeksan PostgreSQL dan
antarmuka metode akses , serta
indeks hash , salah satu metode akses. Kami sekarang akan mempertimbangkan B-tree, indeks yang paling tradisional dan banyak digunakan. Artikel ini besar, jadi bersabarlah.
Btree
Struktur
Jenis indeks B-tree, diimplementasikan sebagai metode akses "btree", cocok untuk data yang dapat diurutkan. Dengan kata lain, operator "lebih besar", "lebih besar atau sama", "kurang", "kurang atau sama", dan "sama" harus ditentukan untuk tipe data. Perhatikan bahwa data yang sama terkadang dapat diurutkan secara berbeda, yang
membawa kita kembali ke konsep keluarga operator.
Seperti biasa, baris indeks B-tree dikemas ke dalam halaman. Di halaman daun, baris ini berisi data yang akan diindeks (kunci) dan referensi ke baris tabel (TIDs). Di halaman internal, setiap baris referensi halaman anak indeks dan berisi nilai minimal di halaman ini.
Pohon-B memiliki beberapa sifat penting:
- Pohon-B seimbang, yaitu, setiap halaman daun dipisahkan dari akar dengan jumlah halaman internal yang sama. Karena itu, mencari nilai apa pun membutuhkan waktu yang sama.
- Pohon-B adalah multi-cabang, yaitu, setiap halaman (biasanya 8 KB) berisi banyak (ratusan) TUT. Akibatnya, kedalaman pohon-B cukup kecil, sebenarnya hingga 4-5 untuk tabel yang sangat besar.
- Data dalam indeks diurutkan dalam urutan nondecreasing (baik antara halaman dan di dalam setiap halaman), dan halaman tingkat yang sama terhubung satu sama lain dengan daftar dua arah. Oleh karena itu, kita bisa mendapatkan kumpulan data yang diurutkan hanya dengan daftar jalan satu atau arah lainnya tanpa kembali ke root setiap kali.
Di bawah ini adalah contoh sederhana dari indeks pada satu bidang dengan kunci integer.
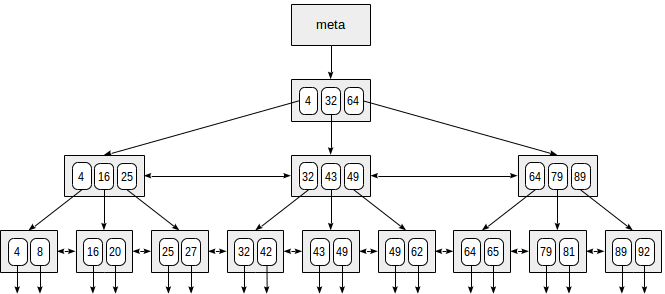
Halaman pertama indeks adalah metapage, yang mereferensikan root indeks. Node internal terletak di bawah root, dan halaman daun berada di baris paling bawah. Panah bawah mewakili referensi dari node daun ke baris tabel (TIDs).
Cari berdasarkan kesetaraan
Mari pertimbangkan pencarian nilai dalam pohon berdasarkan kondisi "
indexed-field =
ekspresi ". Katakanlah, kami tertarik pada kunci 49.

Pencarian dimulai dengan simpul akar, dan kita perlu menentukan ke mana dari simpul anak untuk diturunkan. Menyadari kunci-kunci di simpul akar (4, 32, 64), oleh karena itu kami mencari tahu kisaran nilai dalam simpul anak. Karena 32 ≤ 49 <64, kita perlu turun ke simpul anak kedua. Selanjutnya, proses yang sama diulang secara rekursif sampai kita mencapai simpul daun dari mana TIDs yang dibutuhkan dapat diperoleh.
Pada kenyataannya, sejumlah rincian mempersulit proses yang tampaknya sederhana ini. Misalnya, indeks dapat berisi kunci yang tidak unik dan ada begitu banyak nilai yang sama sehingga tidak cocok dengan satu halaman. Kembali ke contoh kita, tampaknya kita harus turun dari simpul internal atas referensi ke nilai 49. Tapi, seperti yang jelas dari gambar, dengan cara ini kita akan melewati salah satu dari "49" kunci di halaman daun sebelumnya . Oleh karena itu, setelah kami menemukan kunci yang persis sama di halaman internal, kami harus turun satu posisi ke kiri dan kemudian mencari melalui baris indeks dari level yang mendasarinya dari kiri ke kanan untuk mencari kunci yang dicari.
(Komplikasi lain adalah bahwa selama pencarian proses lain dapat mengubah data: pohon dapat dibangun kembali, halaman dapat dibagi menjadi dua, dll. Semua algoritma direkayasa untuk operasi bersamaan ini untuk tidak saling mengganggu satu sama lain dan tidak menyebabkan kunci tambahan sedapat mungkin. Tapi kami akan menghindari memperluas ini.)
Cari berdasarkan ketidaksetaraan
Saat mencari dengan kondisi "
bidang-indeks ≤
ekspresi " (atau "
bidang-indeks ≥
ekspresi "), pertama-tama kita menemukan nilai (jika ada) dalam indeks dengan kondisi kesetaraan "
indeks-bidang =
ekspresi " dan kemudian berjalan melalui halaman daun dalam arah yang sesuai sampai akhir.
Angka tersebut menggambarkan proses ini untuk n ≤ 35:

Operator "lebih besar" dan "kurang" didukung dengan cara yang sama, kecuali bahwa nilai yang awalnya ditemukan harus diturunkan.
Cari berdasarkan rentang
Saat mencari berdasarkan rentang "
ekspresi1 ≤
bidang terindeks ≤
ekspresi2 ", kami menemukan nilai berdasarkan kondisi "
bidang terindeks =
ekspresi1 ", dan kemudian terus berjalan melalui halaman daun sementara kondisi "
bidang terindeks ≤
ekspresi2 " terpenuhi; atau sebaliknya: mulai dengan ekspresi kedua dan berjalan ke arah yang berlawanan sampai kita mencapai ekspresi pertama.
Gambar menunjukkan proses ini untuk kondisi 23 ≤ n ≤ 64:

Contoh
Mari kita lihat contoh seperti apa rencana kueri. Seperti biasa, kami menggunakan database demo, dan kali ini kami akan mempertimbangkan tabel pesawat. Ini berisi sedikitnya sembilan baris, dan perencana akan memilih untuk tidak menggunakan indeks karena seluruh tabel cocok dengan satu halaman. Tetapi tabel ini menarik bagi kita untuk tujuan ilustrasi.
demo=# select * from aircrafts;
aircraft_code | model | range ---------------+---------------------+------- 773 | Boeing 777-300 | 11100 763 | Boeing 767-300 | 7900 SU9 | Sukhoi SuperJet-100 | 3000 320 | Airbus A320-200 | 5700 321 | Airbus A321-200 | 5600 319 | Airbus A319-100 | 6700 733 | Boeing 737-300 | 4200 CN1 | Cessna 208 Caravan | 1200 CR2 | Bombardier CRJ-200 | 2700 (9 rows)
demo=# create index on aircrafts(range); demo=# set enable_seqscan = off;
(Atau secara eksplisit, "buat indeks pada pesawat menggunakan btree (range)", tapi itu adalah B-tree yang dibangun secara default.)
Cari berdasarkan kesetaraan:
demo=# explain(costs off) select * from aircrafts where range = 3000;
QUERY PLAN --------------------------------------------------- Index Scan using aircrafts_range_idx on aircrafts Index Cond: (range = 3000) (2 rows)
Cari berdasarkan ketidaksetaraan:
demo=# explain(costs off) select * from aircrafts where range < 3000;
QUERY PLAN --------------------------------------------------- Index Scan using aircrafts_range_idx on aircrafts Index Cond: (range < 3000) (2 rows)
Dan dengan rentang:
demo=# explain(costs off) select * from aircrafts where range between 3000 and 5000;
QUERY PLAN ----------------------------------------------------- Index Scan using aircrafts_range_idx on aircrafts Index Cond: ((range >= 3000) AND (range <= 5000)) (2 rows)
Menyortir
Sekali lagi mari kita tekankan poin bahwa dengan segala jenis pemindaian (indeks, hanya indeks, atau bitmap), metode akses "btree" mengembalikan data yang dipesan, yang dapat kita lihat dengan jelas pada gambar di atas.
Oleh karena itu, jika tabel memiliki indeks pada kondisi pengurutan, pengoptimal akan mempertimbangkan kedua opsi: pemindaian indeks dari tabel, yang dengan mudah mengembalikan data yang diurutkan, dan pemindaian berurutan dari tabel dengan pengurutan selanjutnya dari hasil.
Sortir pesanan
Saat membuat indeks, kami dapat secara eksplisit menentukan urutan pengurutan. Misalnya, kami dapat membuat indeks berdasarkan rentang penerbangan dengan cara ini khususnya:
demo=# create index on aircrafts(range desc);
Dalam hal ini, nilai yang lebih besar akan muncul di pohon di sebelah kiri, sedangkan nilai yang lebih kecil akan muncul di sebelah kanan. Mengapa ini bisa diperlukan jika kita bisa berjalan melalui nilai yang diindeks di kedua arah?
Tujuannya adalah indeks multi-kolom. Mari kita buat tampilan untuk menunjukkan model pesawat dengan divisi konvensional menjadi pesawat jarak pendek, menengah, dan panjang:
demo=# create view aircrafts_v as select model, case when range < 4000 then 1 when range < 10000 then 2 else 3 end as class from aircrafts; demo=# select * from aircrafts_v;
model | class ---------------------+------- Boeing 777-300 | 3 Boeing 767-300 | 2 Sukhoi SuperJet-100 | 1 Airbus A320-200 | 2 Airbus A321-200 | 2 Airbus A319-100 | 2 Boeing 737-300 | 2 Cessna 208 Caravan | 1 Bombardier CRJ-200 | 1 (9 rows)
Dan mari kita buat indeks (menggunakan ekspresi):
demo=# create index on aircrafts( (case when range < 4000 then 1 when range < 10000 then 2 else 3 end), model);
Sekarang kita dapat menggunakan indeks ini untuk mendapatkan data yang diurutkan berdasarkan kedua kolom dalam urutan menaik:
demo=# select class, model from aircrafts_v order by class, model;
class | model -------+--------------------- 1 | Bombardier CRJ-200 1 | Cessna 208 Caravan 1 | Sukhoi SuperJet-100 2 | Airbus A319-100 2 | Airbus A320-200 2 | Airbus A321-200 2 | Boeing 737-300 2 | Boeing 767-300 3 | Boeing 777-300 (9 rows)
demo=# explain(costs off) select class, model from aircrafts_v order by class, model;
QUERY PLAN -------------------------------------------------------- Index Scan using aircrafts_case_model_idx on aircrafts (1 row)
Demikian pula, kita dapat melakukan kueri untuk mengurutkan data dalam urutan menurun:
demo=# select class, model from aircrafts_v order by class desc, model desc;
class | model -------+--------------------- 3 | Boeing 777-300 2 | Boeing 767-300 2 | Boeing 737-300 2 | Airbus A321-200 2 | Airbus A320-200 2 | Airbus A319-100 1 | Sukhoi SuperJet-100 1 | Cessna 208 Caravan 1 | Bombardier CRJ-200 (9 rows)
demo=# explain(costs off) select class, model from aircrafts_v order by class desc, model desc;
QUERY PLAN ----------------------------------------------------------------- Index Scan BACKWARD using aircrafts_case_model_idx on aircrafts (1 row)
Namun, kami tidak dapat menggunakan indeks ini untuk mendapatkan data yang diurutkan berdasarkan satu kolom dalam urutan menurun dan oleh kolom lainnya dalam urutan naik. Ini akan membutuhkan pengurutan secara terpisah:
demo=# explain(costs off) select class, model from aircrafts_v order by class ASC, model DESC;
QUERY PLAN ------------------------------------------------- Sort Sort Key: (CASE ... END), aircrafts.model DESC -> Seq Scan on aircrafts (3 rows)
(Perhatikan bahwa, sebagai upaya terakhir, perencana memilih pemindaian berurutan terlepas dari pengaturan "enable_seqscan = off" yang dibuat sebelumnya. Ini karena sebenarnya pengaturan ini tidak melarang pemindaian tabel, tetapi hanya menetapkan biaya astronomisnya - silakan lihat paket dengan "Biaya pada".)
Untuk membuat kueri ini menggunakan indeks, yang terakhir harus dibangun dengan arah pengurutan yang diperlukan:
demo=# create index aircrafts_case_asc_model_desc_idx on aircrafts( (case when range < 4000 then 1 when range < 10000 then 2 else 3 end) ASC, model DESC); demo=# explain(costs off) select class, model from aircrafts_v order by class ASC, model DESC;
QUERY PLAN ----------------------------------------------------------------- Index Scan using aircrafts_case_asc_model_desc_idx on aircrafts (1 row)
Urutan kolom
Masalah lain yang muncul saat menggunakan indeks multi-kolom adalah urutan kolom daftar dalam indeks. Untuk B-tree, urutan ini sangat penting: data di dalam halaman akan diurutkan berdasarkan bidang pertama, kemudian oleh yang kedua, dan seterusnya.
Kami dapat mewakili indeks yang kami buat pada interval interval dan model dengan cara simbolis sebagai berikut:

Sebenarnya indeks sekecil itu pasti cocok untuk satu halaman root. Dalam gambar, itu sengaja didistribusikan di antara beberapa halaman untuk kejelasan.
Jelas dari bagan ini bahwa pencarian berdasarkan predikat seperti "class = 3" (pencarian hanya oleh bidang pertama) atau "class = 3 dan model = 'Boeing 777-300'" (pencarian oleh kedua bidang) akan bekerja secara efisien.
Namun, pencarian dengan predikat "model = 'Boeing 777-300'" akan jauh lebih efisien: dimulai dengan root, kita tidak dapat menentukan ke mana simpul anak akan diturunkan, oleh karena itu, kita harus turun ke mereka semua. Ini tidak berarti bahwa indeks seperti ini tidak dapat digunakan - efisiensinya menjadi masalah. Sebagai contoh, jika kita memiliki tiga kelas pesawat dan banyak sekali model di setiap kelas, kita harus melihat sekitar sepertiga dari indeks dan ini mungkin lebih efisien daripada pemindaian tabel penuh ... atau tidak.
Namun, jika kita membuat indeks seperti ini:
demo=# create index on aircrafts( model, (case when range < 4000 then 1 when range < 10000 then 2 else 3 end));
urutan bidang akan berubah:

Dengan indeks ini, pencarian dengan predikat "model = 'Boeing 777-300'" akan bekerja secara efisien, tetapi pencarian dengan predikat "class = 3" tidak akan.
Nulls
Metode akses "Btree" mengindeks NULL dan mendukung pencarian berdasarkan ketentuan IS NULL dan NOT NOT NULL.
Mari kita perhatikan tabel penerbangan, tempat NULL terjadi:
demo=# create index on flights(actual_arrival); demo=# explain(costs off) select * from flights where actual_arrival is null;
QUERY PLAN ------------------------------------------------------- Bitmap Heap Scan on flights Recheck Cond: (actual_arrival IS NULL) -> Bitmap Index Scan on flights_actual_arrival_idx Index Cond: (actual_arrival IS NULL) (4 rows)
NULL terletak di satu atau ujung node daun tergantung pada bagaimana indeks dibuat (NULLS FIRST atau NULLS LAST). Ini penting jika kueri menyertakan pengurutan: indeks dapat digunakan jika perintah SELECT menentukan urutan NULL yang sama dalam klausa ORDER BY sebagai urutan yang ditentukan untuk indeks yang dibuat (NULLS FIRST atau NULLS LAST).
Dalam contoh berikut, pesanan ini sama, oleh karena itu, kami dapat menggunakan indeks:
demo=# explain(costs off) select * from flights order by actual_arrival NULLS LAST;
QUERY PLAN -------------------------------------------------------- Index Scan using flights_actual_arrival_idx on flights (1 row)
Dan di sini pesanan ini berbeda, dan pengoptimal memilih pemindaian berurutan dengan pengurutan berikutnya:
demo=# explain(costs off) select * from flights order by actual_arrival NULLS FIRST;
QUERY PLAN ---------------------------------------- Sort Sort Key: actual_arrival NULLS FIRST -> Seq Scan on flights (3 rows)
Untuk menggunakan indeks, itu harus dibuat dengan NULL yang terletak di awal:
demo=# create index flights_nulls_first_idx on flights(actual_arrival NULLS FIRST); demo=# explain(costs off) select * from flights order by actual_arrival NULLS FIRST;
QUERY PLAN ----------------------------------------------------- Index Scan using flights_nulls_first_idx on flights (1 row)
Masalah seperti ini tentu saja disebabkan oleh NULL yang tidak dapat disortir, yaitu, hasil perbandingan untuk NULL dan nilai lainnya tidak terdefinisi:
demo=# \pset null NULL demo=# select null < 42;
?column? ---------- NULL (1 row)
Ini bertentangan dengan konsep B-tree dan tidak cocok dengan pola umum. Namun, NULL memainkan peran penting dalam basis data sehingga kami selalu harus membuat pengecualian untuknya.
Karena NULLs dapat diindeks, dimungkinkan untuk menggunakan indeks bahkan tanpa persyaratan apa pun yang dikenakan pada tabel (karena indeks berisi informasi tentang semua baris tabel pasti). Ini mungkin masuk akal jika permintaan memerlukan pemesanan data dan indeks memastikan pesanan diperlukan. Dalam hal ini, perencana lebih suka memilih akses indeks untuk menghemat penyortiran terpisah.
Properti
Mari kita lihat properti dari metode akses "btree" (pertanyaan
telah disediakan ).
amname | name | pg_indexam_has_property --------+---------------+------------------------- btree | can_order | t btree | can_unique | t btree | can_multi_col | t btree | can_exclude | t
Seperti yang telah kita lihat, B-tree dapat memesan data dan mendukung keunikan - dan ini adalah satu-satunya metode akses untuk memberi kami properti seperti ini. Indeks multikolom juga diizinkan, tetapi metode akses lainnya (meskipun tidak semuanya) juga dapat mendukung indeks tersebut. Kami akan membahas dukungan batasan EXCLUDE lain kali, dan bukan tanpa alasan.
name | pg_index_has_property ---------------+----------------------- clusterable | t index_scan | t bitmap_scan | t backward_scan | t
Metode akses "Btree" mendukung kedua teknik untuk mendapatkan nilai: pemindaian indeks, serta pemindaian bitmap. Dan seperti yang bisa kita lihat, metode akses dapat berjalan melalui pohon baik "maju" dan "mundur".
name | pg_index_column_has_property --------------------+------------------------------ asc | t desc | f nulls_first | f nulls_last | t orderable | t distance_orderable | f returnable | t search_array | t search_nulls | t
Empat properti pertama dari layer ini menjelaskan bagaimana tepatnya nilai-nilai kolom tertentu tertentu dipesan. Dalam contoh ini, nilai diurutkan dalam urutan naik ("asc") dan NULL diberikan terakhir ("nulls_last"). Tetapi seperti yang telah kita lihat, kombinasi lain dimungkinkan.
Properti "Search_array" menunjukkan dukungan ekspresi seperti ini oleh indeks:
demo=# explain(costs off) select * from aircrafts where aircraft_code in ('733','763','773');
QUERY PLAN ----------------------------------------------------------------- Index Scan using aircrafts_pkey on aircrafts Index Cond: (aircraft_code = ANY ('{733,763,773}'::bpchar[])) (2 rows)
Properti "Dapat dikembalikan" menunjukkan dukungan pemindaian hanya indeks, yang masuk akal karena barisan indeks menyimpan sendiri nilai yang diindeks (misalnya, tidak seperti dalam indeks hash). Di sini masuk akal untuk mengatakan beberapa kata tentang meliputi indeks berdasarkan B-tree.
Indeks unik dengan baris tambahan
Seperti yang kita bahas
sebelumnya , indeks penutup adalah indeks yang menyimpan semua nilai yang diperlukan untuk kueri, akses ke tabel itu sendiri tidak diperlukan (hampir). Indeks unik dapat secara spesifik mencakup.
Tetapi mari kita asumsikan bahwa kita ingin menambahkan kolom tambahan yang diperlukan untuk kueri ke indeks unik. Namun, keunikan dari nilai-nilai komposit tersebut tidak menjamin keunikan kunci, dan kemudian diperlukan dua indeks pada kolom yang sama: satu unik untuk mendukung kendala integritas dan satu lagi untuk digunakan sebagai penutup. Ini tentu saja tidak efisien.
Di perusahaan kami Anastasiya Lubennikova
lubennikovaav meningkatkan metode "btree" sehingga kolom tambahan yang tidak unik dapat dimasukkan dalam indeks yang unik. Kami berharap, tambalan ini akan diadopsi oleh komunitas untuk menjadi bagian dari PostgreSQL, tetapi ini tidak akan terjadi pada awal versi 10. Saat ini, tambalan ini tersedia dalam Pro Standard 9.5+, dan inilah yang terlihat seperti.
Sebenarnya tambalan ini dilakukan untuk PostgreSQL 11.
Mari kita perhatikan tabel pemesanan:
demo=# \d bookings
Table "bookings.bookings" Column | Type | Modifiers --------------+--------------------------+----------- book_ref | character(6) | not null book_date | timestamp with time zone | not null total_amount | numeric(10,2) | not null Indexes: "bookings_pkey" PRIMARY KEY, btree (book_ref) Referenced by: TABLE "tickets" CONSTRAINT "tickets_book_ref_fkey" FOREIGN KEY (book_ref) REFERENCES bookings(book_ref)
Dalam tabel ini, kunci utama (book_ref, kode pemesanan) disediakan oleh indeks "btree" biasa. Mari kita buat indeks unik baru dengan kolom tambahan:
demo=# create unique index bookings_pkey2 on bookings(book_ref) INCLUDE (book_date);
Sekarang kami mengganti indeks yang ada dengan yang baru (dalam transaksi, untuk menerapkan semua perubahan secara bersamaan):
demo=# begin; demo=# alter table bookings drop constraint bookings_pkey cascade; demo=# alter table bookings add primary key using index bookings_pkey2; demo=# alter table tickets add foreign key (book_ref) references bookings (book_ref); demo=# commit;
Inilah yang kami dapatkan:
demo=# \d bookings
Table "bookings.bookings" Column | Type | Modifiers --------------+--------------------------+----------- book_ref | character(6) | not null book_date | timestamp with time zone | not null total_amount | numeric(10,2) | not null Indexes: "bookings_pkey2" PRIMARY KEY, btree (book_ref) INCLUDE (book_date) Referenced by: TABLE "tickets" CONSTRAINT "tickets_book_ref_fkey" FOREIGN KEY (book_ref) REFERENCES bookings(book_ref)
Sekarang satu dan indeks yang sama berfungsi sebagai unik dan berfungsi sebagai indeks penutup untuk permintaan ini, misalnya:
demo=# explain(costs off) select book_ref, book_date from bookings where book_ref = '059FC4';
QUERY PLAN -------------------------------------------------- Index Only Scan using bookings_pkey2 on bookings Index Cond: (book_ref = '059FC4'::bpchar) (2 rows)
Pembuatan indeks
Sudah terkenal, namun tidak kalah pentingnya, bahwa untuk tabel ukuran besar, lebih baik memuat data di sana tanpa indeks dan membuat indeks yang diperlukan nanti. Ini tidak hanya lebih cepat, tetapi kemungkinan besar indeks akan memiliki ukuran lebih kecil.
Masalahnya adalah bahwa penciptaan indeks "btree" menggunakan proses yang lebih efisien daripada penyisipan nilai-nilai baris ke pohon. Secara kasar, semua data yang tersedia di tabel diurutkan, dan halaman daun dari data ini dibuat. Kemudian halaman internal "dibangun di atas" basis ini sampai seluruh piramida menyatu ke root.
Kecepatan proses ini tergantung pada ukuran RAM yang tersedia, yang dibatasi oleh parameter "maintenance_work_mem". Jadi, meningkatkan nilai parameter dapat mempercepat proses. Untuk indeks unik, memori ukuran "work_mem" dialokasikan di samping "maintenance_work_mem".
Semantik perbandingan
Terakhir kali kami menyebutkan bahwa PostgreSQL perlu tahu fungsi hash mana yang membutuhkan nilai dari tipe yang berbeda dan bahwa asosiasi ini disimpan dalam metode akses "hash". Demikian juga, sistem harus mencari cara untuk memesan nilai. Ini diperlukan untuk pengurutan, pengelompokan (kadang-kadang), gabung bergabung, dan sebagainya. PostgreSQL tidak mengikat dirinya sendiri ke nama operator (seperti>, <, =) karena pengguna dapat menentukan tipe data mereka sendiri dan memberikan nama yang berbeda kepada operator yang sesuai. Keluarga operator yang digunakan oleh metode akses "btree" mendefinisikan nama operator sebagai gantinya.
Misalnya, operator perbandingan ini digunakan dalam keluarga operator "bool_ops":
postgres=# select amop.amopopr::regoperator as opfamily_operator, amop.amopstrategy from pg_am am, pg_opfamily opf, pg_amop amop where opf.opfmethod = am.oid and amop.amopfamily = opf.oid and am.amname = 'btree' and opf.opfname = 'bool_ops' order by amopstrategy;
opfamily_operator | amopstrategy ---------------------+-------------- <(boolean,boolean) | 1 <=(boolean,boolean) | 2 =(boolean,boolean) | 3 >=(boolean,boolean) | 4 >(boolean,boolean) | 5 (5 rows)
Di sini kita dapat melihat lima operator pembanding, tetapi seperti yang telah disebutkan, kita tidak boleh mengandalkan nama mereka. Untuk mengetahui perbandingan yang dilakukan masing-masing operator, konsep strategi diperkenalkan. Lima strategi didefinisikan untuk menggambarkan semantik operator:
- 1 - kurang
- 2 - kurang atau sama
- 3 - sama
- 4 - lebih besar atau sama
- 5 - lebih besar
Beberapa keluarga operator dapat berisi beberapa operator yang menerapkan satu strategi. Misalnya, keluarga operator "integer_ops" berisi operator berikut untuk strategi 1:
postgres=# select amop.amopopr::regoperator as opfamily_operator from pg_am am, pg_opfamily opf, pg_amop amop where opf.opfmethod = am.oid and amop.amopfamily = opf.oid and am.amname = 'btree' and opf.opfname = 'integer_ops' and amop.amopstrategy = 1 order by opfamily_operator;
opfamily_operator ---------------------- <(integer,bigint) <(smallint,smallint) <(integer,integer) <(bigint,bigint) <(bigint,integer) <(smallint,integer) <(integer,smallint) <(smallint,bigint) <(bigint,smallint) (9 rows)
Berkat ini, pengoptimal dapat menghindari gips saat membandingkan nilai berbagai jenis yang terkandung dalam satu keluarga operator.
Dukungan indeks untuk tipe data baru
Dokumentasi menyediakan
contoh pembuatan tipe data baru untuk bilangan kompleks dan kelas operator untuk mengurutkan nilai tipe ini. Contoh ini menggunakan bahasa C, yang benar-benar masuk akal ketika kecepatan sangat penting. Tapi tidak ada yang menghalangi kita menggunakan SQL murni untuk percobaan yang sama hanya untuk mencoba dan lebih memahami semantik perbandingan.
Mari kita buat tipe komposit baru dengan dua bidang: bagian nyata dan imajiner.
postgres=# create type complex as (re float, im float);
Kita bisa membuat tabel dengan bidang tipe baru dan menambahkan beberapa nilai ke tabel:
postgres=# create table numbers(x complex); postgres=# insert into numbers values ((0.0, 10.0)), ((1.0, 3.0)), ((1.0, 1.0));
Sekarang muncul pertanyaan: bagaimana cara memesan bilangan kompleks jika tidak ada hubungan urutan didefinisikan untuk mereka dalam arti matematika?
Ternyata, operator perbandingan sudah ditentukan untuk kami:
postgres=# select * from numbers order by x;
x -------- (0,10) (1,1) (1,3) (3 rows)
Secara default, pengurutan adalah komponen untuk jenis komposit: bidang pertama dibandingkan, lalu bidang kedua, dan seterusnya, kira-kira sama dengan cara string teks dibandingkan karakter per karakter. Tetapi kita dapat mendefinisikan urutan yang berbeda. Sebagai contoh, bilangan kompleks dapat diperlakukan sebagai vektor dan dipesan oleh modulus (panjang), yang dihitung sebagai akar kuadrat dari jumlah kuadrat dari koordinat (teorema Pythagoras '). Untuk mendefinisikan urutan seperti itu, mari kita buat fungsi bantu yang menghitung modulus:
postgres=# create function modulus(a complex) returns float as $$ select sqrt(a.re*a.re + a.im*a.im); $$ immutable language sql;
Sekarang kita akan secara sistematis menentukan fungsi untuk semua lima operator pembanding yang menggunakan fungsi bantu ini:
postgres=# create function complex_lt(a complex, b complex) returns boolean as $$ select modulus(a) < modulus(b); $$ immutable language sql; postgres=# create function complex_le(a complex, b complex) returns boolean as $$ select modulus(a) <= modulus(b); $$ immutable language sql; postgres=# create function complex_eq(a complex, b complex) returns boolean as $$ select modulus(a) = modulus(b); $$ immutable language sql; postgres=# create function complex_ge(a complex, b complex) returns boolean as $$ select modulus(a) >= modulus(b); $$ immutable language sql; postgres=# create function complex_gt(a complex, b complex) returns boolean as $$ select modulus(a) > modulus(b); $$ immutable language sql;
Dan kami akan membuat operator yang sesuai. Untuk mengilustrasikan bahwa mereka tidak perlu dipanggil ">", "<", dan seterusnya, mari kita beri mereka nama "aneh".
postgres=# create operator #<#(leftarg=complex, rightarg=complex, procedure=complex_lt); postgres=# create operator #<=#(leftarg=complex, rightarg=complex, procedure=complex_le); postgres=# create operator #=#(leftarg=complex, rightarg=complex, procedure=complex_eq); postgres=# create operator #>=#(leftarg=complex, rightarg=complex, procedure=complex_ge); postgres=# create operator #>#(leftarg=complex, rightarg=complex, procedure=complex_gt);
Pada titik ini, kita dapat membandingkan angka:
postgres=# select (1.0,1.0)::complex #<# (1.0,3.0)::complex;
?column? ---------- t (1 row)
Selain lima operator, metode akses "btree" memerlukan satu fungsi lagi (berlebihan tetapi nyaman) untuk didefinisikan: harus mengembalikan -1, 0, atau 1 jika nilai pertama kurang dari, sama dengan, atau lebih besar dari yang kedua satu. Fungsi bantu ini disebut dukungan. Metode akses lain dapat memerlukan pendefinisian fungsi pendukung lainnya.
postgres=# create function complex_cmp(a complex, b complex) returns integer as $$ select case when modulus(a) < modulus(b) then -1 when modulus(a) > modulus(b) then 1 else 0 end; $$ language sql;
Sekarang kita siap untuk membuat kelas operator (dan keluarga operator dengan nama yang sama akan dibuat secara otomatis):
postgres=# create operator class complex_ops default for type complex using btree as operator 1 #<#, operator 2 #<=#, operator 3 #=#, operator 4 #>=#, operator 5 #>#, function 1 complex_cmp(complex,complex);
Sekarang penyortiran berfungsi seperti yang diinginkan:
postgres=# select * from numbers order by x;
x -------- (1,1) (1,3) (0,10) (3 rows)
Dan itu pasti akan didukung oleh indeks "btree".
Untuk melengkapi gambar, Anda bisa mendapatkan fungsi dukungan menggunakan kueri ini:
postgres=# select amp.amprocnum, amp.amproc, amp.amproclefttype::regtype, amp.amprocrighttype::regtype from pg_opfamily opf, pg_am am, pg_amproc amp where opf.opfname = 'complex_ops' and opf.opfmethod = am.oid and am.amname = 'btree' and amp.amprocfamily = opf.oid;
amprocnum | amproc | amproclefttype | amprocrighttype -----------+-------------+----------------+----------------- 1 | complex_cmp | complex | complex (1 row)
Internal
Kita dapat menjelajahi struktur internal B-tree menggunakan ekstensi "pageinspect".
demo=# create extension pageinspect;
Indeks metapage:
demo=# select * from bt_metap('ticket_flights_pkey');
magic | version | root | level | fastroot | fastlevel --------+---------+------+-------+----------+----------- 340322 | 2 | 164 | 2 | 164 | 2 (1 row)
Yang paling menarik di sini adalah level indeks: indeks pada dua kolom untuk sebuah tabel dengan satu juta baris diperlukan hanya 2 level (tidak termasuk root).
Informasi statistik pada blok 164 (root):
demo=# select type, live_items, dead_items, avg_item_size, page_size, free_size from bt_page_stats('ticket_flights_pkey',164);
type | live_items | dead_items | avg_item_size | page_size | free_size ------+------------+------------+---------------+-----------+----------- r | 33 | 0 | 31 | 8192 | 6984 (1 row)
Dan data di blok (bidang "data", yang di sini dikorbankan untuk lebar layar, berisi nilai kunci pengindeksan dalam representasi biner):
demo=# select itemoffset, ctid, itemlen, left(data,56) as data from bt_page_items('ticket_flights_pkey',164) limit 5;
itemoffset | ctid | itemlen | data ------------+---------+---------+---------------------------------------------------------- 1 | (3,1) | 8 | 2 | (163,1) | 32 | 1d 30 30 30 35 34 33 32 33 30 35 37 37 31 00 00 ff 5f 00 3 | (323,1) | 32 | 1d 30 30 30 35 34 33 32 34 32 33 36 36 32 00 00 4f 78 00 4 | (482,1) | 32 | 1d 30 30 30 35 34 33 32 35 33 30 38 39 33 00 00 4d 1e 00 5 | (641,1) | 32 | 1d 30 30 30 35 34 33 32 36 35 35 37 38 35 00 00 2b 09 00 (5 rows)
Elemen pertama berkaitan dengan teknik dan menentukan batas atas semua elemen dalam blok (detail implementasi yang tidak kami diskusikan), sedangkan data itu sendiri dimulai dengan elemen kedua. Jelas bahwa simpul anak paling kiri adalah blok 163, diikuti oleh blok 323, dan seterusnya. Mereka, pada gilirannya, dapat dieksplorasi menggunakan fungsi yang sama.
Sekarang, mengikuti tradisi yang baik, masuk akal untuk membaca dokumentasi,
README , dan kode sumber.
Namun satu ekstensi yang berpotensi lebih bermanfaat adalah "
amcheck ", yang akan dimasukkan dalam PostgreSQL 10, dan untuk versi yang lebih rendah Anda bisa mendapatkannya dari
github . Ekstensi ini memeriksa konsistensi logis dari data dalam B-tree dan memungkinkan kami untuk mendeteksi kesalahan sebelumnya.
Itu benar, "amcheck" adalah bagian dari PostgreSQL mulai dari versi 10.
Baca terus .