Akhirnya, sebuah panduan berbahasa Rusia untuk bahasa Julia muncul. Ini memberikan pengantar lengkap untuk bahasa bagi mereka yang memiliki sedikit pengalaman dalam pemrograman (sisanya akan berguna untuk pengembangan umum), ada juga pengantar pembelajaran mesin dan banyak tugas untuk mengkonsolidasikan materi.
Selama pencarian, saya menemukan kursus pemrograman untuk para ekonom (selain Julia, ada juga Python). Berpengalaman dapat mengikuti kursus singkat atau membaca buku How to Think Like a Computer Scientist
Berikut ini adalah terjemahan materi dari blog Christopher Rackauckas 7 Julia Gotchas dan Cara Menangani Mereka
Mari saya mulai dengan mengatakan bahwa Julia adalah bahasa yang indah. Saya mencintainya, inilah yang saya anggap sebagai bahasa yang paling kuat dan intuitif yang pernah saya gunakan. Tidak diragukan lagi ini adalah bahasa favorit saya. Namun, ada beberapa 'jebakan', hal-hal kecil yang rumit yang perlu Anda ketahui. Setiap bahasa memiliki mereka, dan salah satu hal pertama yang harus Anda lakukan untuk menguasai bahasa adalah untuk mengetahui apa itu dan bagaimana menghindarinya. Maksud dari posting ini adalah untuk membantu Anda mempercepat proses ini dengan mengungkap beberapa
Julia adalah bahasa yang baik untuk memahami apa yang terjadi, karena tidak ada keajaiban di dalamnya. Pengembang Julia ingin memiliki aturan perilaku yang jelas. Ini berarti bahwa semua perilaku dapat dijelaskan. Namun, ini mungkin berarti Anda harus berusaha keras untuk memahami mengapa hal ini dan bukan yang lain terjadi. Itu sebabnya saya tidak hanya akan menjelaskan beberapa masalah umum, tetapi saya juga akan menjelaskan mengapa mereka muncul. Anda akan melihat bahwa ada beberapa pola yang sangat mirip, dan begitu Anda menyadarinya, Anda tidak akan lagi melakukan kesalahan. Karena itu, Julia memiliki kurva belajar yang sedikit lebih curam dibandingkan dengan bahasa yang lebih sederhana seperti MATLAB / R / Python . Namun, setelah Anda menguasainya, Anda akan dapat sepenuhnya memanfaatkan singkatnya Julia dalam mendapatkan kinerja C / Fortran . Sekarang gali lebih dalam.
Tanpa diduga: REPL (terminal) memiliki cakupan global
Sejauh ini, ini adalah masalah paling umum yang dilaporkan oleh pengguna baru Julia. Seseorang akan berkata: "Saya dengar, Julia cepat!", Buka REPL, cepat tulis beberapa algoritma terkenal dan jalankan skrip ini. Setelah eksekusi, mereka melihat waktu dan berkata: "Tunggu sebentar, mengapa lambat, seperti di Python?" Karena ini adalah masalah yang begitu penting dan umum, mari kita luangkan waktu menjelajahi alasan mengapa hal ini terjadi untuk mencari tahu bagaimana cara menghindarinya.
Penyimpangan kecil: mengapa Julia cepat
Anda harus memahami bahwa Julia tidak hanya kompilasi kode, tetapi juga spesialisasi tipe (yaitu, kompilasi kode yang spesifik untuk tipe ini). Biarkan saya ulangi: Julia tidak cepat, karena kode dikompilasi menggunakan kompiler JIT, bukan rahasia kecepatan adalah kode jenis-spesifik dikompilasi.
Jika Anda membutuhkan cerita lengkap, lihat beberapa catatan yang saya tulis untuk seminar mendatang . Jenis spesifisitas ditentukan oleh prinsip dasar desain Julia: pengiriman ganda . Ketika Anda menulis kode:
function f(a,b) return 2a+b end
Tampaknya ini hanya satu f(2.0,3.0) , Julia akan menjalankan kode yang dikompilasi, yang mengambil dua angka floating point dan mengembalikan 2a + b . Jika Anda memanggil f(2,3) , maka Julia akan menjalankan kode kompilasi lain yang mengambil dua bilangan bulat dan mengembalikan 2a + b . Fungsi f adalah abstraksi atau singkatan untuk berbagai metode yang memiliki bentuk yang sama, dan skema penggunaan simbol f untuk memanggil semua metode yang berbeda ini disebut pengiriman ganda. Dan ini berlaku di mana-mana: operator + sebenarnya adalah fungsi yang akan memanggil metode tergantung pada jenis yang dilihatnya. Julia benar-benar mendapatkan kecepatannya karena kode yang dikompilasi olehnya mengetahui tipenya, dan oleh karena itu kode yang dikompilasi yang memanggil f (2.0,3.0) adalah persis kode terkompilasi yang Anda dapatkan dengan mendefinisikan fungsi yang sama di C / Fortran . Anda dapat memeriksa ini dengan makro code_native untuk melihat kumpulan yang dikompilasi:
@code_native f(2.0,3.0)
pushq %rbp movq %rsp, %rbp Source line: 2 vaddsd %xmm0, %xmm0, %xmm0 vaddsd %xmm1, %xmm0, %xmm0 popq %rbp retq nop
Ini adalah kumpulan terkompilasi yang sama yang Anda harapkan dari fungsi di C / Fortran , dan berbeda dari kode perakitan untuk bilangan bulat:
@code_native f(2,3) pushq %rbp movq %rsp, %rbp Source line: 2 leaq (%rdx,%rcx,2), %rax popq %rbp retq nopw (%rax,%rax)
Esensi: REPL / Global Scope tidak mengizinkan tipe spesifik
Ini membawa kita ke poin utama: REPL / Global Scope lambat karena tidak memungkinkan spesifikasi tipe. Pertama-tama, perhatikan bahwa REPL adalah ruang lingkup global karena Julia memungkinkan ruang bersarang untuk fungsi. Misalnya, jika kita mendefinisikan
function outer() a = 5 function inner() return 2a end b = inner() return 3a+b end
kita akan melihat bahwa kode ini berfungsi. Ini karena Julia memungkinkan Anda untuk menangkap dari fungsi eksternal ke fungsi internal. Jika Anda menerapkan ide ini secara berulang , Anda akan menyadari bahwa area tertinggi adalah area yang langsung REPL (yang merupakan lingkup global dari modul Utama ). Tapi sekarang mari kita pikirkan bagaimana fungsi akan dikompilasi dalam situasi ini. Kami menerapkan hal yang sama, tetapi menggunakan variabel global:
a=2.0; b=3.0 function linearcombo() return 2a+b end ans = linearcombo()
dan
a = 2; b = 3 ans2= linearcombo()
Pertanyaan: Jenis apa yang harus diterima oleh kompiler untuk a dan b ? Perhatikan bahwa dalam contoh ini, kami mengubah jenis dan masih memanggil fungsi yang sama. Itu dapat menangani semua jenis yang kita tambahkan: mengambang, bilangan bulat, array, tipe pengguna aneh, dll. Di Julia, ini berarti bahwa variabel harus kotak, dan jenis diperiksa setiap kali mereka digunakan. Menurut Anda seperti apa kode yang dikompilasi?
Tebal pushq %rbp movq %rsp, %rbp pushq %r15 pushq %r14 pushq %r12 pushq %rsi pushq %rdi pushq %rbx subq $96, %rsp movl $2147565792, %edi # imm = 0x800140E0 movabsq $jl_get_ptls_states, %rax callq *%rax movq %rax, %rsi leaq -72(%rbp), %r14 movq $0, -88(%rbp) vxorps %xmm0, %xmm0, %xmm0 vmovups %xmm0, -72(%rbp) movq $0, -56(%rbp) movq $10, -104(%rbp) movq (%rsi), %rax movq %rax, -96(%rbp) leaq -104(%rbp), %rax movq %rax, (%rsi) Source line: 3 movq pcre2_default_compile_context_8(%rdi), %rax movq %rax, -56(%rbp) movl $2154391480, %eax # imm = 0x806967B8 vmovq %rax, %xmm0 vpslldq $8, %xmm0, %xmm0 # xmm0 = zero,zero,zero,zero,zero,zero,zero,zero,xmm0[0,1,2,3,4,5,6,7] vmovdqu %xmm0, -80(%rbp) movq %rdi, -64(%rbp) movabsq $jl_apply_generic, %r15 movl $3, %edx movq %r14, %rcx callq *%r15 movq %rax, %rbx movq %rbx, -88(%rbp) movabsq $586874896, %r12 # imm = 0x22FB0010 movq (%r12), %rax testq %rax, %rax jne L198 leaq 98096(%rdi), %rcx movabsq $jl_get_binding_or_error, %rax movl $122868360, %edx # imm = 0x752D288 callq *%rax movq %rax, (%r12) L198: movq 8(%rax), %rax testq %rax, %rax je L263 movq %rax, -80(%rbp) addq $5498232, %rdi # imm = 0x53E578 movq %rdi, -72(%rbp) movq %rbx, -64(%rbp) movq %rax, -56(%rbp) movl $3, %edx movq %r14, %rcx callq *%r15 movq -96(%rbp), %rcx movq %rcx, (%rsi) addq $96, %rsp popq %rbx popq %rdi popq %rsi popq %r12 popq %r14 popq %r15 popq %rbp retq L263: movabsq $jl_undefined_var_error, %rax movl $122868360, %ecx # imm = 0x752D288 callq *%rax ud2 nopw (%rax,%rax)
Untuk bahasa dinamis tanpa jenis spesialisasi, kode kembung ini dengan semua instruksi tambahan sebaik yang Anda bisa, jadi Julia memperlambat kecepatannya. Untuk memahami mengapa ini sangat penting, perhatikan bahwa setiap bagian dari kode yang Anda tulis di Julia mengkompilasi. Katakanlah Anda menulis satu loop di skrip Anda:
a = 1 for i = 1:100 a += a + f(a) end
Compiler harus mengkompilasi loop ini, tetapi karena itu tidak dapat menjamin bahwa tipe tidak berubah, itu secara konservatif membungkus footcloth pada semua tipe, yang mengarah pada eksekusi yang lambat.
Bagaimana cara menghindari masalah
Ada beberapa cara untuk menghindari masalah ini. Cara termudah adalah dengan selalu membungkus skrip Anda dalam fungsi. Misalnya, kode sebelumnya akan berbentuk:
function geta(a) # can also just define a=1 here for i = 1:100 a += a + f(a) end return a end a = geta(1)
Ini akan memberi Anda hasil yang sama, tetapi karena kompiler dapat berspesialisasi dalam tipe a , itu akan memberikan kode terkompilasi yang Anda inginkan. Hal lain yang dapat Anda lakukan adalah mendefinisikan variabel Anda sebagai konstanta.
const b = 5
Dengan melakukan ini, Anda memberi tahu kompiler bahwa variabel tidak akan berubah, dan dengan demikian ia akan dapat mengkhususkan semua kode yang menggunakannya pada tipe yang sekarang. Ada sedikit kekhasan bahwa Julia benar-benar memungkinkan Anda untuk mengubah nilai konstanta, tetapi bukan tipe. Jadi, Anda bisa menggunakan const untuk memberi tahu kompiler bahwa Anda tidak akan mengubah jenisnya. Namun, perhatikan bahwa ada beberapa kebiasaan kecil:
const a = 5 f() = a println(f()) # Prints 5 a = 6 println(f()) # Prints 5 # WARNING: redefining constant a
ini tidak bekerja seperti yang diharapkan, karena kompiler, menyadari bahwa dia tahu jawaban untuk f () = a (karena a adalah konstanta), cukup mengganti pemanggilan fungsi dengan jawaban, memberikan perilaku yang berbeda daripada jika a tidak konstan.
Moral: jangan menulis skrip Anda langsung di REPL, selalu bungkus dalam suatu fungsi.
Nezhdanchik dua: Ketidakstabilan tipe
Jadi, saya baru saja menyatakan pendapat tentang betapa pentingnya spesialisasi kode untuk tipe data. Izinkan saya mengajukan pertanyaan, apa yang terjadi ketika tipe Anda dapat berubah? Jika Anda menebak: "Ya, dalam hal ini, Anda tidak dapat mengkhususkan kode yang dikompilasi," maka Anda benar. Masalah seperti itu dikenal sebagai ketidakstabilan tipe. Mereka mungkin muncul secara berbeda, tetapi satu contoh umum adalah bahwa Anda menginisialisasi nilai dengan yang sederhana, tetapi tidak harus tipe yang seharusnya. Sebagai contoh, mari kita lihat:
function g() x=1 for i = 1:10 x = x/2 end return x end
Perhatikan bahwa 1/2 adalah angka floating point di Julia. Oleh karena itu, jika kita mulai dengan x = 1 , bilangan bulat akan berubah menjadi angka floating-point, dan dengan demikian, fungsi harus mengkompilasi loop batin, seolah-olah bisa dari jenis apa pun. Jika sebaliknya kita punya:
function h() x=1.0 for i = 1:10 x = x/2 end return x end
maka seluruh fungsi akan dapat dikompilasi secara optimal, mengetahui bahwa x akan tetap menjadi angka floating point (kemampuan ini bagi kompiler untuk menentukan jenis disebut tipe inferensi). Kami dapat memeriksa kode yang dikompilasi untuk melihat perbedaannya:
Alas kaki asli pushq %rbp movq %rsp, %rbp pushq %r15 pushq %r14 pushq %r13 pushq %r12 pushq %rsi pushq %rdi pushq %rbx subq $136, %rsp movl $2147565728, %ebx # imm = 0x800140A0 movabsq $jl_get_ptls_states, %rax callq *%rax movq %rax, -152(%rbp) vxorps %xmm0, %xmm0, %xmm0 vmovups %xmm0, -80(%rbp) movq $0, -64(%rbp) vxorps %ymm0, %ymm0, %ymm0 vmovups %ymm0, -128(%rbp) movq $0, -96(%rbp) movq $18, -144(%rbp) movq (%rax), %rcx movq %rcx, -136(%rbp) leaq -144(%rbp), %rcx movq %rcx, (%rax) movq $0, -88(%rbp) Source line: 4 movq %rbx, -104(%rbp) movl $10, %edi leaq 477872(%rbx), %r13 leaq 10039728(%rbx), %r15 leaq 8958904(%rbx), %r14 leaq 64(%rbx), %r12 leaq 10126032(%rbx), %rax movq %rax, -160(%rbp) nopw (%rax,%rax) L176: movq %rbx, -128(%rbp) movq -8(%rbx), %rax andq $-16, %rax movq %r15, %rcx cmpq %r13, %rax je L272 movq %rbx, -96(%rbp) movq -160(%rbp), %rcx cmpq $2147419568, %rax # imm = 0x7FFF05B0 je L272 movq %rbx, -72(%rbp) movq %r14, -80(%rbp) movq %r12, -64(%rbp) movl $3, %edx leaq -80(%rbp), %rcx movabsq $jl_apply_generic, %rax vzeroupper callq *%rax movq %rax, -88(%rbp) jmp L317 nopw %cs:(%rax,%rax) L272: movq %rcx, -120(%rbp) movq %rbx, -72(%rbp) movq %r14, -80(%rbp) movq %r12, -64(%rbp) movl $3, %r8d leaq -80(%rbp), %rdx movabsq $jl_invoke, %rax vzeroupper callq *%rax movq %rax, -112(%rbp) L317: movq (%rax), %rsi movl $1488, %edx # imm = 0x5D0 movl $16, %r8d movq -152(%rbp), %rcx movabsq $jl_gc_pool_alloc, %rax callq *%rax movq %rax, %rbx movq %r13, -8(%rbx) movq %rsi, (%rbx) movq %rbx, -104(%rbp) Source line: 3 addq $-1, %rdi jne L176 Source line: 6 movq -136(%rbp), %rax movq -152(%rbp), %rcx movq %rax, (%rcx) movq %rbx, %rax addq $136, %rsp popq %rbx popq %rdi popq %rsi popq %r12 popq %r13 popq %r14 popq %r15 popq %rbp retq nop
menentang
Mantra assembler yang rapi pushq %rbp movq %rsp, %rbp movabsq $567811336, %rax # imm = 0x21D81D08 Source line: 6 vmovsd (%rax), %xmm0 # xmm0 = mem[0],zero popq %rbp retq nopw %cs:(%rax,%rax)
Perbedaan dalam jumlah perhitungan untuk mendapatkan nilai yang sama!
Cara menemukan dan menangani ketidakstabilan tipe

Pada titik ini, Anda mungkin bertanya: "Nah, mengapa tidak menggunakan C saja sehingga Anda tidak perlu mencari ketidakstabilan ini?" Jawabannya adalah:
- Mudah ditemukan
- Mereka mungkin membantu.
Anda dapat menangani ketidakstabilan dengan hambatan fungsional
Julia memberi Anda makro code_warntype untuk menunjukkan di mana ketidakstabilan tipe. Misalnya, jika kita menggunakan ini dalam fungsi g kita buat:
@code_warntype g()
dapatkan analisisnya Variables: #self#::#g x::ANY #temp#@_3::Int64 i::Int64 #temp#@_5::Core.MethodInstance #temp#@_6::Float64 Body: begin x::ANY = 1 # line 3: SSAValue(2) = (Base.select_value)((Base.sle_int)(1,10)::Bool,10,(Base.box)(Int64,(Base.sub_int)(1,1)))::Int64 #temp#@_3::Int64 = 1 5: unless (Base.box)(Base.Bool,(Base.not_int)((#temp#@_3::Int64 === (Base.box)(Int64,(Base.add_int)(SSAValue(2),1)))::Bool)) goto 30 SSAValue(3) = #temp#@_3::Int64 SSAValue(4) = (Base.box)(Int64,(Base.add_int)(#temp#@_3::Int64,1)) i::Int64 = SSAValue(3) #temp#@_3::Int64 = SSAValue(4) # line 4: unless (Core.isa)(x::UNION{FLOAT64,INT64},Float64)::ANY goto 15 #temp#@_5::Core.MethodInstance = MethodInstance for /(::Float64, ::Int64) goto 24 15: unless (Core.isa)(x::UNION{FLOAT64,INT64},Int64)::ANY goto 19 #temp#@_5::Core.MethodInstance = MethodInstance for /(::Int64, ::Int64) goto 24 19: goto 21 21: #temp#@_6::Float64 = (x::UNION{FLOAT64,INT64} / 2)::Float64 goto 26 24: #temp#@_6::Float64 = $(Expr(:invoke, :(#temp#@_5), :(Main./), :(x::Union{Float64,Int64}), 2)) 26: x::ANY = #temp#@_6::Float64 28: goto 5 30: # line 6: return x::UNION{FLOAT64,INT64} end::UNION{FLOAT64,INT64}
Perhatikan bahwa pada awalnya kita mengatakan bahwa tipe x adalah Any . Ini akan menggunakan tipe apa pun yang tidak ditetapkan sebagai strict type , yaitu tipe abstrak yang perlu dikotak / dicentang pada setiap langkah. Kita melihat bahwa pada akhirnya kita mengembalikan x sebagai UNION {FLOAT64, INT64} , yang merupakan tipe non-ketat lainnya. Ini memberitahu kita bahwa tipe code_warntype untuk h , kita mendapatkan semua tipe ketat:
@code_warntype h() Variables: #self#::#h x::Float64 #temp#::Int64 i::Int64 Body: begin x::Float64 = 1.0 # line 3: SSAValue(2) = (Base.select_value)((Base.sle_int)(1,10)::Bool,10,(Base.box)(Int64,(Base.sub_int)(1,1)))::Int64 #temp#::Int64 = 1 5: unless (Base.box)(Base.Bool,(Base.not_int)((#temp#::Int64 === (Base.box)(Int64,(Base.add_int)(SSAValue(2),1)))::Bool)) goto 15 SSAValue(3) = #temp#::Int64 SSAValue(4) = (Base.box)(Int64,(Base.add_int)(#temp#::Int64,1)) i::Int64 = SSAValue(3) #temp#::Int64 = SSAValue(4) # line 4: x::Float64 = (Base.box)(Base.Float64,(Base.div_float)(x::Float64,(Base.box)(Float64,(Base.sitofp)(Float64,2)))) 13: goto 5 15: # line 6: return x::Float64 end::Float64
Ini menunjukkan bahwa fungsi tersebut adalah tipe stable dan pada dasarnya akan mengkompilasi menjadi kode C yang optimal. Dengan demikian, ketidakstabilan jenis tidak sulit ditemukan. Yang lebih sulit adalah menemukan desain yang tepat. Mengapa mengatasi ketidakstabilan tipe? Ini adalah masalah lama yang telah menyebabkan fakta bahwa bahasa yang diketik secara dinamis mendominasi bidang permainan skrip. Idenya adalah bahwa dalam banyak kasus Anda ingin menemukan kompromi antara kinerja dan keandalan.
Misalnya, Anda bisa membaca tabel dari halaman web di mana bilangan bulat dicampur dengan angka floating point. Di Julia, Anda dapat menulis fungsi Anda sehingga jika semuanya adalah bilangan bulat, itu mengkompilasi dengan baik, dan jika semuanya adalah angka floating point, itu juga mengkompilasi dengan baik. Dan jika mereka dicampur? Ini masih akan berfungsi. Ini adalah fleksibilitas / kenyamanan yang kita ketahui dan sukai dari bahasa seperti Python / R. Tetapi Julia akan memberi tahu Anda secara langsung ( melalui code_warntype ) ketika Anda mengorbankan kinerja.
Bagaimana menangani ketidakstabilan tipe
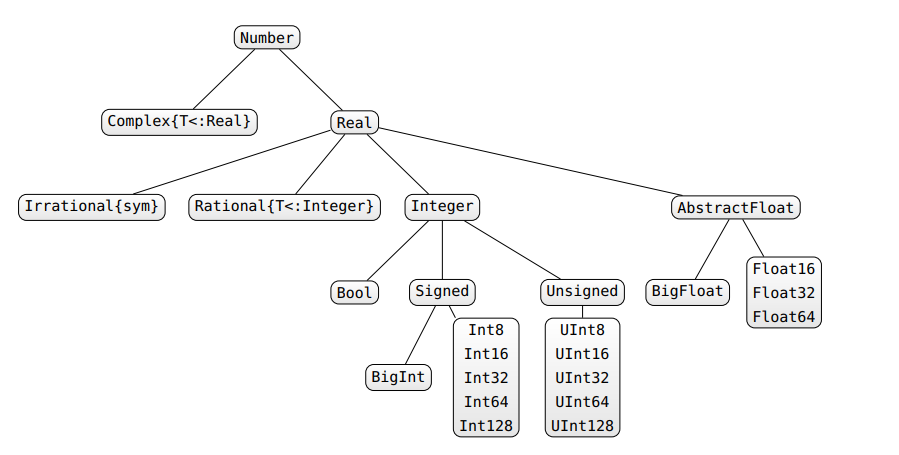
Ada beberapa cara untuk mengatasi ketidakstabilan tipe. Pertama-tama, jika Anda menyukai sesuatu seperti C / Fortran di mana tipe Anda dideklarasikan dan tidak dapat diubah (yang memastikan stabilitas tipe), Anda dapat melakukan ini di Julia:
local a::Int64 = 5
Ini membuat bilangan bulat 64-bit, dan jika kode di masa depan mencoba mengubahnya, pesan kesalahan akan dihasilkan (atau konversi yang benar akan dilakukan. Tetapi karena konversi tidak akan dibulatkan secara otomatis, kemungkinan besar akan menyebabkan kesalahan). Taburkan di sekitar kode Anda dan Anda mendapatkan stabilitas tipe, ala, C / Fortran . Cara yang tidak terlalu rumit untuk menangani ini adalah dengan pernyataan tipe. Di sini Anda meletakkan sintaks yang sama di sisi lain dari tanda sama dengan. Sebagai contoh:
a = (b/c)::Float64
Tampaknya mengatakan: "hitung b / c dan pastikan bahwa outputnya adalah Float64. Jika tidak, cobalah untuk melakukan konversi otomatis. Jika konversi tidak dapat dilakukan dengan mudah, hasilkan kesalahan." Menempatkan desain seperti itu akan membantu Anda memastikan Anda tahu jenis apa yang terlibat. Namun, dalam beberapa kasus, ketidakstabilan jenis diperlukan. Misalnya, katakan Anda ingin memiliki kode yang dapat diandalkan, tetapi pengguna memberi Anda sesuatu yang gila, seperti:
arr = Vector{Union{Int64,Float64}}(undef, 4) arr[1]=4 arr[2]=2.0 arr[3]=3.2 arr[4]=1
yang merupakan array bilangan bulat 4x1 dan angka floating point. Jenis elemen aktual untuk array adalah Union {Int64, Float64} , yang, seperti yang kita lihat sebelumnya, tidak ketat, yang dapat menyebabkan masalah. Kompiler hanya tahu bahwa setiap nilai dapat berupa bilangan bulat atau angka titik mengambang, tetapi bukan elemen jenis apa. Ini berarti naif untuk melakukan aritmatika dengan array ini, misalnya:
function foo{T,N}(array::Array{T,N}) for i in eachindex(array) val = array[i] # do algorithm X on val end end
akan lambat karena operasi akan dikotak. Namun, kami dapat menggunakan beberapa pengiriman untuk menjalankan kode dengan cara yang khusus. Ini dikenal sebagai menggunakan hambatan fungsional. Sebagai contoh:
function inner_foo{T<:Number}(val::T) # Do algorithm X on val end function foo2{T,N}(array::Array{T,N}) for i in eachindex(array) inner_foo(array[i]) end end
Perhatikan bahwa karena beberapa pengiriman, memanggil panggilan inner_foo baik metode yang dikompilasi khusus untuk angka floating point atau metode yang dikompilasi khusus untuk bilangan bulat. Dengan demikian, Anda bisa meletakkan perhitungan panjang di inner_foo dan tetap membuatnya bekerja dengan baik, tidak kalah dengan pengetikan ketat yang diberikan penghalang fungsional.
Jadi, saya harap Anda melihat bahwa Julia menawarkan kombinasi yang baik antara kinerja pengetikan yang kuat dan kenyamanan pengetikan dinamis. Seorang programmer yang baik, Julia, memiliki kedua opsi untuk memaksimalkan produktivitas dan / atau produktivitas jika perlu.
Kejutan 3: Eval bekerja secara global

Salah satu kekuatan terbesar Julia adalah kemampuan pemrogramannya. Ini memungkinkan Anda untuk dengan mudah menulis program penghasil kode, secara efektif mengurangi jumlah kode yang perlu Anda tulis dan pertahankan. Makro adalah fungsi yang berjalan pada waktu kompilasi dan (biasanya) mengeluarkan kode. Sebagai contoh:
macro defa() :(a=5) end
akan mengganti instance defa dengan kode a = 5 ( :(a = 5) yang dikutip ekspresi . Kode Julia adalah ekspresi, dan karenanya metaprogramming adalah kumpulan ekspresi).
Anda dapat menggunakan ini untuk membangun program Julia kompleks apa pun yang Anda inginkan dan menjalankannya sebagai jenis pintasan yang benar-benar cerdas. Namun, kadang-kadang Anda mungkin perlu mengevaluasi kode yang dihasilkan secara langsung. Julia memberi Anda fungsi eval atau makro makro untuk melakukan ini. Secara umum, Anda harus mencoba menghindari eval , tetapi ada beberapa kode yang diperlukan, misalnya, perpustakaan baru saya untuk mentransfer data antara berbagai proses untuk pemrograman paralel . , , :
@eval :(a=5)
(REPL). , / . Sebagai contoh:
function testeval() @eval :(a=5) return 2a+5 end
, a REPL. , , :
function testeval() @eval :(a=5) b = a::Int64 return 2b+5 end
b — , , , , , . eval , , REPL .
4:
Julia , . : , .
, ? , , . Sebagai contoh:
a = 2 + 3 + 4 + 5 + 6 + 7 +8 + 9 + 10+ 11+ 12+ 13 a
, 90, 27. ? a = 2 + 3 + 4 + 5 + 6 + 7 , a = 27 , +8 + 9 + 10+ 11+ 12+ 13 , , , :
a = 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10+ 11+ 12+ 13
90, . , .
. — , . rssdev10
. Sebagai contoh:
x = rand(2,2) a = [cos(2*pi.*x[:,1]).*cos(2*pi.*x[:,2])./(4*pi) -sin(2.*x[:,1]).*sin(2.*x[:,2])./(4)] b = [cos(2*pi.*x[:,1]).*cos(2*pi.*x[:,2])./(4*pi) - sin(2.*x[:,1]).*sin(2.*x[:,2])./(4)]
, a b — , ! (2,2) , — (1-) 2. , , :
a = [1 -2] b = [1 - 2]
: 1 -2 . : 1-2 . - . :
a = [1 2 3 -4 2 -3 1 4]
2x4. , . : hcat :
a = hcat(cos(2*pi.*x[:,1]).*cos(2*pi.*x[:,2])./(4*pi),-sin(2.*x[:,1]).*sin(2.*x[:,2])./(4))
!
№5: ,

(View) — () , ( ), .
, , . , . , .
— "". ""
a = [3;4;5] b = a b[1] = 1
, a — [1; 4; 5] , . . b a . , b = a b a . , , b , , ( b a ). , . , , :
a = rand(2,2) # Makes a random 2x2 matrix b = vec(a) # Makes a view to the 2x2 matrix which is a 1-dimensional array
b , b a , b . , , ( , ). . , . Sebagai contoh:
c = a[1:2,1]
c a ). , , , , . , , :
d = @view a[1:2,1] e = view(a,1:2,1)
d , e — , d e a , , , reshape , .) , . Sebagai contoh:
a[1:2,1] = [1;2]
a , a[1:2,1] view (a, 1:2,1) , , a . -? , :
b = copy(a)
, b a , , b a . a , copy! (B, a) , a a ( , b ). . , Vector {Vector} :
a = [ [1, 2, 3], [4, 5], [6, 7, 8, 9] ]
b = copy(a) b[1][1] = 10 a
3-element Array{Array{Int64,1},1}: [10, 2, 3] [4, 5] [6, 7, 8, 9]
, a[1][1] 10! ? copy a . a , b , b . , deepcopy :
b = deepcopy(a)
, . , , .
№6: , In-Place
MATLAB / Python / R . Julia , , , " ".
function f() x = [1;5;6] for i = 1:10 x = x + inner(x) end return x end function inner(x) return 2x end
, inner , , 2x . , . , - y , :
function f() x = [1;5;6] y = Vector{Int64}(3) for i = 1:10 inner(y,x) for i in 1:3 x[i] = x[i] + y[i] end copy!(y,x) end return x end function inner!(y,x) for i=1:3 y[i] = 2*x[i] end nothing end
. inner!(y, x) , y . y , y , , , inner! (y, x) ! ( ).
, inner!(y, x) . copy!(y, x) — , x y , . , , . : x y . , x + inner(x) , , , 11 . , .
, , , . - ( loop-fusion ). Julia v0.5 . ( ( broadcast ), f.(x) — , f x , , . f x , x = x + f. (x) . :
x .= x .+ f.(x)
.= , , ,
for i = 1:length(x) x[i] = x[i] + f(x[i]) end
, :
function f() x = [1;5;6] for i = 1:10 x .= x .+ inner.(x) end return x end function inner(x) return 2x end
MATLAB / R / Python , , , .
: ,
: , . , . , . , , . , .
- , C / Fortran , . - , , !
: ? , . , , ? [ , Javascript var x = 3 x , x = 3 x . ? , - Javascript!]