Pendahuluan:Sejumlah besar masalah paling beragam yang berkaitan dengan hampir semua cabang fisika matematika yang paling penting dan dirancang untuk menjawab pertanyaan teknis topikal terkait dengan penerapan fungsi Bessel.
Fungsi Bessel banyak digunakan dalam menyelesaikan masalah akustik, radiofisika, hidrodinamika, masalah atom dan fisika nuklir. Banyak aplikasi fungsi Bessel untuk teori konduktivitas termal dan teori elastisitas (masalah pada getaran pelat, masalah teori shell, masalah menentukan konsentrasi tegangan dekat retakan)
Popularitas fungsi Bessel tersebut dijelaskan oleh fakta bahwa penyelesaian persamaan fisika matematika yang mengandung operator Laplace dalam koordinat silindris dengan metode klasik pemisahan variabel mengarah ke persamaan diferensial biasa, yang berfungsi untuk menentukan fungsi-fungsi ini [1].
Fungsi Bessel dinamai astronom Jerman Friedrich Bessel, yang pada tahun 1824, mempelajari gerakan planet di sekitar matahari, memperoleh hubungan perulangan untuk fungsi Bessel
Jv(x) diterima untuk bilangan bulat
v representasi integral dari suatu fungsi
Jv(x) , membuktikan adanya nol fungsi yang tak terhitung jumlahnya
J0(x) dan menyusun tabel pertama untuk fungsi
J1(x) dan
J2(x) .
Namun, untuk pertama kalinya salah satu fungsi Bessel
J0(x) Itu dianggap kembali pada 1732 oleh Daniel Bernoulli dalam sebuah karya yang ditujukan untuk osilasi rantai berat. D. Bernoulli menemukan ekspresi fungsi
J0(x) dalam bentuk seri kekuatan dan memperhatikan (tanpa bukti) bahwa persamaan
J0(x)=0 memiliki akar valid yang tak terhitung jumlahnya.
Karya berikutnya, di mana fungsi Bessel ditemui, adalah karya Leonardo Euler pada 1738, yang dikhususkan untuk studi getaran dari membran melingkar. Dalam karya ini, L. Euler ditemukan untuk bilangan bulat
v Ekspresi fungsi Bessel
Jv(x) dalam bentuk serangkaian kekuatan
x , dan dalam makalah berikutnya memperluas ungkapan ini untuk kasus nilai indeks sewenang-wenang
v . Selain itu, L. Euler membuktikan itu untuk
v sama dengan bilangan bulat dan setengah, fungsi
Jv(x) diekspresikan melalui fungsi-fungsi dasar.
Dia mencatat (tanpa bukti) bahwa dengan valid
v fungsi
Jv(x) memiliki nol nyata yang tak terhitung jumlahnya dan memberikan representasi integral untuk
Jv(x) . Beberapa peneliti percaya bahwa hasil utama yang terkait dengan fungsi Bessel dan aplikasinya dalam fisika matematika dihubungkan dengan nama L. Euler.
Untuk mempelajari properti fungsi Bessel dan pada saat yang sama menguasai metode untuk menyelesaikan persamaan yang direduksi menjadi fungsi Bessel, memungkinkan program matematika simbolik SymPy - the Python library yang didistribusikan secara bebas.
Dalam program matematika simbolik SymPy, grafik fungsi Bessel dari jenis pertama dari bilangan bulat pesanan dapat dibangun menggunakan relasi untuk jumlah seri:
Jp(x)= sum inftym=0 fracx2m+p(−1)m22m+pm! Gamma(p+m+1)
Fungsi Bessel dari jenis pertamafrom sympy import* from sympy.plotting import plot x,n, p=var('x,n, p') def besselj(p,x): return summation(((-1)**n*x**(2*n+p))/(factorial(n)*gamma(n+p+1)*2**(2*n+p)),[n,0,oo]) st="J_{p}(x)" p1=plot(besselj(0,x),(x,-20,20),line_color='b',title=' $'+st+ '$',show=False) p2=plot(besselj(1,x),(x,-20,20),line_color='g',show=False) p3=plot(besselj(2,x),(x,-20,20),line_color='r',show=False) p4=plot(besselj(3,x),(x,-20,20),line_color='c',show=False) p1.extend(p2) p1.extend(p3) p1.extend(p4) p1.show()
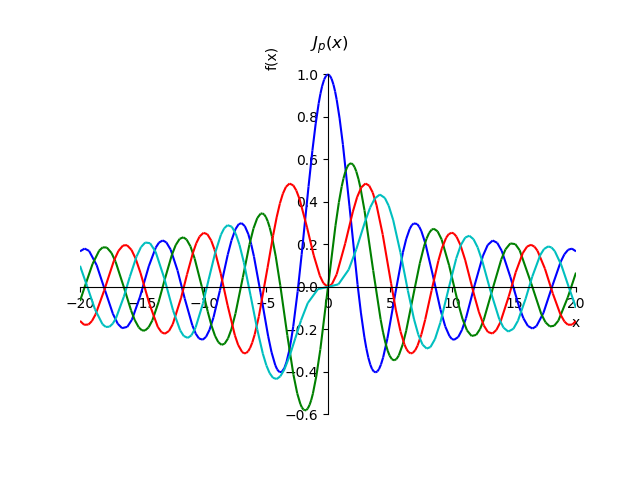
Dengan menggunakan relasi untuk jumlah seri, kami dapat membuktikan properti dari fungsi-fungsi ini untuk seluruh pesanan
J1(x)=−J−1(x):
Properti fungsi Bessel jenis pertama from sympy import* from sympy.plotting import plot x,n, p=var('x,n, p') def besselj(p,x): return summation(((-1)**n*x**(2*n+p))/(factorial(n)*gamma(n+p+1)*2**(2*n+p)),[n,0,oo]) st="J_{1}(x)=-J_{-1}(x)" p1=plot(besselj(1,x),(x,-10,10),line_color='b',title=' $'+st+ '$',show=False) p2=plot(besselj(-1,x),(x,-10,10),line_color='r',show=False) p1.extend(p2) p1.show()

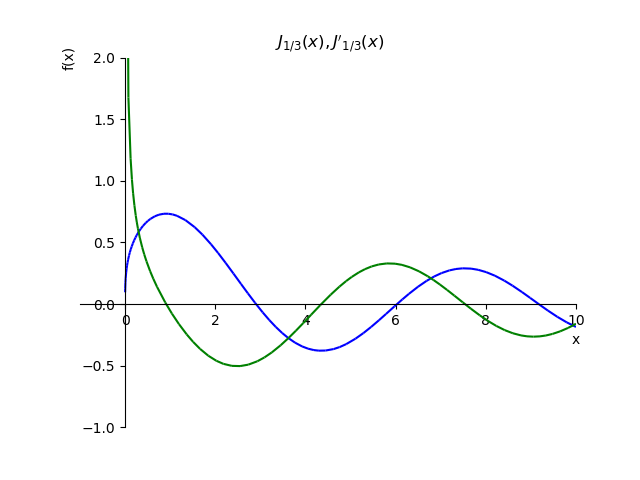
Untuk menunjukkan kondisi Cauchy, kami membangun sebuah fungsi
J1/3(x) dan turunannya
fracdJ1/3(x)dx: :
Fungsi urutan pecahan dan turunannya from sympy import* from sympy.plotting import plot x,n, p=var('x,n, p') def besselj(p,x): return summation(((-1)**n*x**(2*n+p))/(factorial(n)*gamma(n+p+1)*2**(2*n+p)),[n,0,oo]) st="J_{1/3}(x),J{}'_{1/3}(x)" p1=plot(besselj(1/3,x),(x,-1,10),line_color='b',title=' $'+st+ '$',ylim=(-1,2),show=False) def dbesselj(p,x): return diff(summation(((-1)**n*x**(2*n+p))/(factorial(n)*gamma(n+p+1)*2**(2*n+p)),[n,0,oo]),x) p2=plot(dbesselj(1/3,x),(x,-1,10),line_color='g',show=False) p1.extend(p2) p1.show()
Namun, untuk perhitungan praktis, modul mpmath yang luar biasa digunakan, yang memungkinkan tidak hanya menyelesaikan persamaan dengan fungsi Bessel jenis pertama dan kedua, termasuk yang dimodifikasi dari semua pesanan yang dapat diterima, tetapi juga membuat grafik dengan penskalaan otomatis.
Selain itu, modul mpmath tidak memerlukan alat khusus untuk berbagi matematika simbolik dan numerik. Sejarah pembuatan modul ini dan kemungkinan penggunaannya untuk transformasi Laplace terbalik telah saya pertimbangkan dalam publikasi [2]. Sekarang kami melanjutkan diskusi mpmath untuk bekerja dengan fungsi Bessel [3].
Fungsi Bessel dari jenis pertama JN(x)mpmath.besselj (n, x, turunan = 0) - memberikan fungsi Bessel dari jenis pertama
Jn(x) . Fungsi
JN(x) adalah solusi untuk persamaan diferensial berikut:
x2y″+xy′+(x2−n2)y=0
Untuk semuanya positif
n berperilaku seperti sinus atau kosinus, dikalikan dengan koefisien yang perlahan-lahan berkurang
x rightarrow pm inftyFungsi Bessel dari jenis pertama
JN(x) adalah kasus khusus fungsi hipergeometrik
oF1 :
Jn(x)= fracxn2n Gamma(n+1)oF1(n+1, fracx24)
Fungsi Bessel dapat dibedakan
m kali asalkan turunan ke-saya tidak sama dengan nol:
fracdmdxmJn(x)
Fungsi Bessel dari jenis pertama
JN(x) untuk pesanan bilangan bulat positif n = 0,1,2,3 - solusi dari persamaan Bessel:
from mpmath import* j0 = lambda x: besselj(0,x) j1 = lambda x: besselj(1,x) j2 = lambda x: besselj(2,x) j3 = lambda x: besselj(3,x) plot([j0,j1,j2,j3],[0,14]

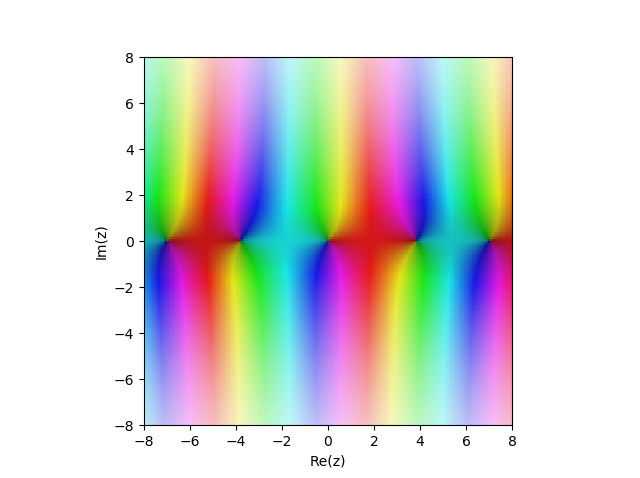
Fungsi Bessel dari jenis pertama
JN(x) di bidang kompleks:
from sympy import* from mpmath import* cplot(lambda z: besselj(1,z), [-8,8], [-8,8], points=50000)
Contoh:
Fungsi
besselj(N,x) memberikan hasil dengan jumlah digit tertentu
(mp.dps) setelah koma:
from mpmath import* mp.dps = 15; mp.pretty = True print(besselj(2, 1000)) nprint(besselj(4, 0.75)) nprint(besselj(2, 1000j)) mp.dps = 25 nprint( besselj(0.75j, 3+4j)) mp.dps = 50 nprint( besselj(1, pi))
Argumen fungsi bisa berupa sejumlah besar:
from mpmath import* mp.dps = 25 nprint( besselj(0, 10000)) nprint(besselj(0, 10**10)) nprint(besselj(2, 10**100)) nprint( besselj(2, 10**5*j))
Fungsi Bessel dari jenis pertama memenuhi simetri sederhana sehubungan dengan
x=0 :
from sympy import* from mpmath import* mp.dps = 15 nprint([besselj(n,0) for n in range(5)]) nprint([besselj(n,pi) for n in range(5)]) nprint([besselj(n,-pi) for n in range(5)])
Akar tidak periodik, tetapi jarak antara akar berturut mendekati tanpa gejala
2π . Fungsi Bessel dari jenis pertama memiliki kode berikut:
from mpmath import* print(quadosc(j0, [0, inf], period=2*pi)) print(quadosc(j1, [0, inf], period=2*pi))
Untuk
n=1/2 atau
n=−1/2 Fungsi Bessel direduksi menjadi fungsi trigonometri:
from sympy import* from mpmath import* x = 10 print(besselj(0.5, x)) print(sqrt(2/(pi*x))*sin(x)) print(besselj(-0.5, x)) print(sqrt(2/(pi*x))*cos(x))
Derivatif pesanan apa pun dapat dihitung,
pesanan negatif terkait dengan integrasi :
from mpmath import* mp.dps = 25 print(besselj(0, 7.5, 1)) print(diff(lambda x: besselj(0,x), 7.5)) print(besselj(0, 7.5, 10)) print(diff(lambda x: besselj(0,x), 7.5, 10)) print(besselj(0,7.5,-1) - besselj(0,3.5,-1)) print(quad(j0, [3.5, 7.5]))
Diferensiasi dengan orde non-integer memberikan turunan fraksional dalam arti integral diferensial Riemann-Liouville, dihitung menggunakan fungsi
difint() :
from mpmath import* mp.dps = 15 print(besselj(1, 3.5, 0.75)) print(differint(lambda x: besselj(1, x), 3.5, 0.75))
Cara lain untuk memanggil fungsi Bessel dari jenis pertama nol dan urutan pertama
mpmath.j0 (x) - Menghitung fungsi Bessel
J0(x) ;
mpmath.j1 (x) - Menghitung fungsi Bessel
J1(x) ;
Fungsi Bessel dari jenis keduabessely (n, x, turunan = 0) Menghitung fungsi Bessel jenis kedua dari relasi:
Yn(x)= fracJn(x)cos( pi cdotn)−J−n(x)sin( pi cdotn)
Untuk bilangan bulat
n Rumus berikut harus dipahami sebagai batas. Fungsi Bessel dapat dibedakan
m kali asalkan turunan ke-saya tidak sama dengan nol:
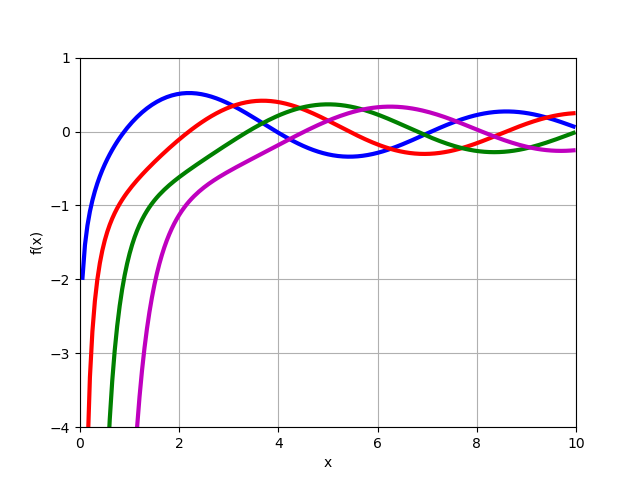
fracdmdxmYn(x)Fungsi Bessel dari jenis kedua
Yn(x) untuk pesanan positif bilangan bulat
n=0,1,2,3 .
from sympy import* from mpmath import* y0 = lambda x: bessely(0,x) y1 = lambda x: bessely(1,x) y2 = lambda x: bessely(2,x) y3 = lambda x: bessely(3,x) plot([y0,y1,y2,y3],[0,10],[-4,1])
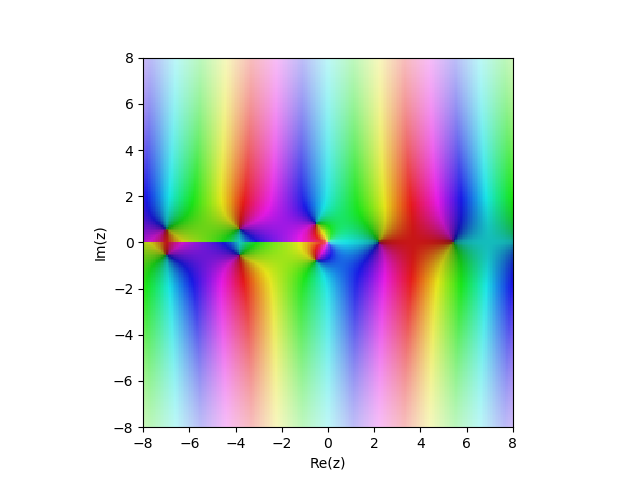
Fungsi Bessel jenis 2
Yn(x) di bidang kompleks
from sympy import* from mpmath import* cplot(lambda z: bessely(1,z), [-8,8], [-8,8], points=50000)
Contoh:
Beberapa nilai fungsi
Yn(x) :
from sympy import* from mpmath import* mp.dps = 25; mp.pretty = True print(bessely(0,0)) print(bessely(1,0)) print(bessely(2,0)) print(bessely(1, pi)) print(bessely(0.5, 3+4j))
Argumen bisa jadi besar:
from sympy import* from mpmath import* mp.dps = 25; mp.pretty = True print(bessely(0, 10000)) print(bessely(2.5, 10**50)) print(bessely(2.5, -10**50))
Derivatif pesanan apa pun, termasuk negatif, dapat dihitung:
from sympy import* from mpmath import* mp.dps = 25; mp.pretty = True print(bessely(2, 3.5, 1)) print(diff(lambda x: bessely(2, x), 3.5)) print(bessely(0.5, 3.5, 1)) print(diff(lambda x: bessely(0.5, x), 3.5)) print(diff(lambda x: bessely(2, x), 0.5, 10)) print(bessely(2, 0.5, 10)) print(bessely(2, 100.5, 100)) print(quad(lambda x: bessely(2,x), [1,3])) print(bessely(2,3,-1) - bessely(2,1,-1))
Fungsi Bessel yang dimodifikasi dari jenis pertama
mpmath.besseli(n, x, derivative=0)
besseli (n, x, turunan = 0) memodifikasi fungsi Bessel dari jenis pertama
In(x)= mathiti−nJn(ix)
fracdmdxmIn(x)
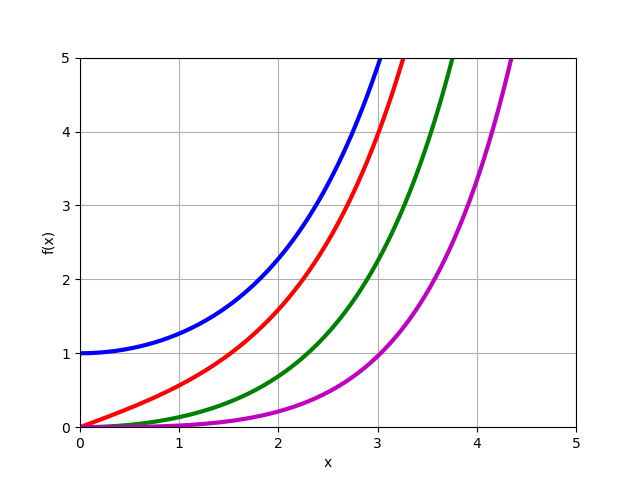
Fungsi Bessel yang Dimodifikasi
In(x) untuk pesanan nyata
n=0,1,2,3 :
from mpmath import* i0 = lambda x: besseli(0,x) i1 = lambda x: besseli(1,x) i2 = lambda x: besseli(2,x) i3 = lambda x: besseli(3,x) plot([i0,i1,i2,i3],[0,5],[0,5])
Fungsi Bessel yang Dimodifikasi
In(x) di bidang kompleks
from mpmath import* cplot(lambda z: besseli(1,z), [-8,8], [-8,8], points=50000)

Contoh:
Beberapa arti
In(x) from mpmath import* mp.dps = 25; mp.pretty = True print(besseli(0,0)) print(besseli(1,0)) print(besseli(0,1)) print(besseli(3.5, 2+3j))
Argumen bisa jadi besar:
from mpmath import* mp.dps = 25; mp.pretty = True print(besseli(2, 1000)) print(besseli(2, 10**10)) print(besseli(2, 6000+10000j))
Untuk bilangan bulat n, representasi integral berikut ini berlaku:
from mpmath import* mp.dps = 15; mp.pretty = True n = 3 x = 2.3 print(quad(lambda t: exp(x*cos(t))*cos(n*t), [0,pi])/pi) print(besseli(n,x))
Derivatif pesanan apa pun dapat dihitung:
from mpmath import* mp.dps = 25; mp.pretty = True print(besseli(2, 7.5, 1)) print(diff(lambda x: besseli(2,x), 7.5)) print(besseli(2, 7.5, 10)) print(diff(lambda x: besseli(2,x), 7.5, 10)) print(besseli(2,7.5,-1) - besseli(2,3.5,-1)) print(quad(lambda x: besseli(2,x), [3.5, 7.5]))
Fungsi Bessel yang dimodifikasi dari jenis kedua,
mpmath.besselk(n, x)
besselk (n, x) memodifikasi fungsi Bessel jenis kedua
Kn(x)= frac pi4 fracI−n(x)−In(x)sin( pi cdotn)
Untuk bilangan bulat
n rumus ini harus dipahami sebagai batasan.
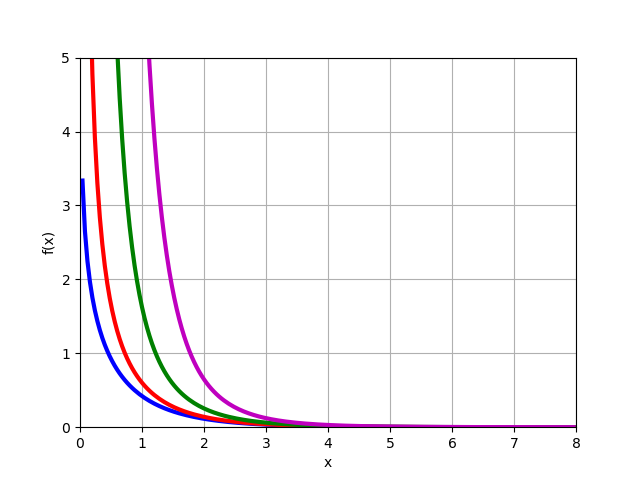
Fungsi Bessel yang dimodifikasi dari jenis kedua
Kn(x) untuk material
n=0,1,2,3 :
from mpmath import* k0 = lambda x: besselk(0,x) k1 = lambda x: besselk(1,x) k2 = lambda x: besselk(2,x) k3 = lambda x: besselk(3,x) plot([k0,k1,k2,k3],[0,8],[0,5])
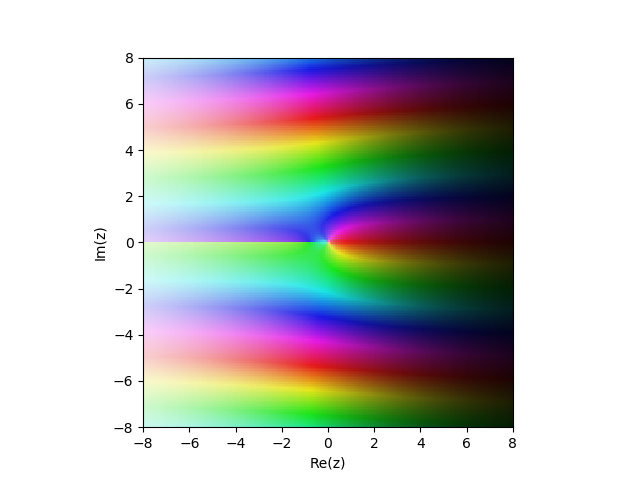
Fungsi Bessel yang dimodifikasi dari jenis kedua
Kn(x)) di bidang kompleks
from mpmath import* cplot(lambda z: besselk(1,z), [-8,8], [-8,8], points=50000)
Contoh:
Argumen yang rumit dan kompleks:
from mpmath import * mp.dps = 25; mp.pretty = True print(besselk(0,1)) print(besselk(0, -1)) print(besselk(3.5, 2+3j)) print(besselk(2+3j, 0.5))
Argumen adalah Bilangan Besar
from mpmath import * mp.dps = 25; mp.pretty = True print(besselk(0, 100)) print(besselk(1, 10**6)) print(besselk(1, 10**6*j)) print(besselk(4.5, fmul(10**50, j, exact=True)))
Fitur perilaku fungsi pada suatu titik
x=0 :
from mpmath import * print(besselk(0,0)) print(besselk(1,0)) for n in range(-4, 5): print(besselk(n, '1e-1000'))
Fungsi Bessel Nol besseljzero() mpmath.besseljzero(v, m, derivative=0)
Untuk pesanan nyata
mathit nu geq0 dan bilangan bulat positif
m kembali
j nu,m , nol positif pertama dari fungsi Bessel jenis pertama
J nu(z) (lihat
besselj () ). Atau, dengan
derivatif=1 memberikan nol perdana non-negatif pertama
j′ nu,m dari
J′ nu(z) . Penunjukan perjanjian pengindeksan menggunakan Abramowitz & Stegun dan DLMF. Perhatikan kasus khusus.
j′0,1=0 sementara semua nol lainnya positif.
Pada kenyataannya, hanya nol sederhana yang dihitung (semua nol dari fungsi Bessel sederhana, kecuali kapan
z=0 ), dan
j nu,m menjadi fungsi monoton dari
nu dan
m . Nol bergantian sesuai dengan ketidaksetaraan:
j′ nu,k<j nu,k<j′ nu,k+1
j nu,1<j nu+1,2<j nu,2<j nu+1,2<j nu,3 cdots
Contoh:
Memimpin nol fungsi Bessel
J0(z) ,
J1(z) ,
J2(z) from mpmath import * mp.dps = 25; mp.pretty = True print(besseljzero(0,1)) print(besseljzero(0,2)) print(besseljzero(0,3)) print(besseljzero(1,1)) print(besseljzero(1,2)) print(besseljzero(1,3)) print(besseljzero(2,1)) print(besseljzero(2,2)) print(besseljzero(2,3))
Memimpin nol turunan dari fungsi Bessel
J′0(z) ,
J′1(z) ,
J′2(z) from mpmath import * mp.dps = 25; mp.pretty = True print(besseljzero(0,1,1)) print(besseljzero(0,2,1)) print(besseljzero(0,3,1)) print(besseljzero(1,1,1)) print(besseljzero(1,2,1)) print(besseljzero(1,3,1)) print(besseljzero(2,1,1)) print(besseljzero(2,2,1)) print(besseljzero(2,3,1))
Nol dengan indeks besar:
from mpmath import * mp.dps = 25; mp.pretty = True print(besseljzero(0,100)) print(besseljzero(0,1000)) print(besseljzero(0,10000)) print(besseljzero(5,100)) print(besseljzero(5,1000)) print(besseljzero(5,10000)) print(besseljzero(0,100,1)) print(besseljzero(0,1000,1)) print(besseljzero(0,10000,1))
Nol fungsi dengan pesanan besar:
from mpmath import * mp.dps = 25; mp.pretty = True print(besseljzero(50,1)) print(besseljzero(50,2)) print(besseljzero(50,100)) print(besseljzero(50,1,1)) print(besseljzero(50,2,1)) print(besseljzero(50,100,1))
Nol fungsi dengan urutan fraksional:
from mpmath import * mp.dps = 25; mp.pretty = True print(besseljzero(0.5,1)) print(besseljzero(1.5,1)) print(besseljzero(2.25,4))
Dan
J nu(z) . dan
J′ nu(z) dapat dinyatakan sebagai produk tanpa batas di nol mereka:
from mpmath import * mp.dps = 6; mp.pretty = True v,z = 2, mpf(1) nprint((z/2)**v/gamma(v+1) * \ nprod(lambda k: 1-(z/besseljzero(v,k))**2, [1,inf])) print(besselj(v,z)) nprint((z/2)**(v-1)/2/gamma(v) * \ nprod(lambda k: 1-(z/besseljzero(v,k,1))**2, [1,inf])) print(besselj(v,z,1))
besselyzero() mpmath.besselyzero(v, m, derivative=0)
Untuk pesanan nyata
mathit nu geq0 dan bilangan bulat positif
m kembali
y nu,m ,
m , nol positif positif dari jenis kedua dari fungsi Bessel
Y nu(z) (lihat
Bessely () ). Atau, dengan
derivatif=1 memberikan nol positif pertama
y′ nu,m dari
Y′ nu(z) . Nol bergantian sesuai dengan ketidaksetaraan:
y nu,k<y′ nu,k<y nu,k+1
y nu,1<y nu+1,2<y nu,2<y nu+1,2<y nu,3 cdots
Contoh:
Memimpin nol fungsi Bessel
Y0(z) ,
Y1(z) ,
Y2(z) from mpmath import * mp.dps = 25; mp.pretty = True print(besselyzero(0,1)) print(besselyzero(0,2)) print(besselyzero(0,3)) print(besselyzero(1,1)) print(besselyzero(1,2)) print(besselyzero(1,3)) print(besselyzero(2,1)) print(besselyzero(2,2)) print(besselyzero(2,3))
Memimpin nol turunan dari fungsi Bessel
Y′0(z) ,
Y′1(z) ,
Y′2(z) from mpmath import * mp.dps = 25; mp.pretty = True print(besselyzero(0,1,1)) print(besselyzero(0,2,1)) print(besselyzero(0,3,1)) print(besselyzero(1,1,1)) print(besselyzero(1,2,1)) print(besselyzero(1,3,1)) print(besselyzero(2,1,1)) print(besselyzero(2,2,1)) print(besselyzero(2,3,1))
Nol dengan indeks besar:
from mpmath import * mp.dps = 25; mp.pretty = True print(besselyzero(0,100)) print(besselyzero(0,1000)) print(besselyzero(0,10000)) print(besselyzero(5,100)) print(besselyzero(5,1000)) print(besselyzero(5,10000)) print(besselyzero(0,100,1)) print(besselyzero(0,1000,1)) print(besselyzero(0,10000,1))
Nol fungsi dengan pesanan besar:
from mpmath import * mp.dps = 25; mp.pretty = True print(besselyzero(50,1)) print(besselyzero(50,2)) print(besselyzero(50,100)) print(besselyzero(50,1,1)) print(besselyzero(50,2,1)) print(besselyzero(50,100,1))
Nol fungsi dengan urutan fraksional:
from mpmath import * mp.dps = 25; mp.pretty = True print(besselyzero(0.5,1)) print(besselyzero(1.5,1)) print(besselyzero(2.25,4))
Aplikasi Fungsi BesselPentingnya fungsi Bessel bukan hanya karena seringnya muncul persamaan Bessel dalam aplikasi, tetapi juga pada kenyataan bahwa solusi dari banyak persamaan diferensial linier orde dua lainnya dapat diekspresikan dalam hal fungsi Bessel. Untuk melihat bagaimana mereka muncul, kita mulai dengan persamaan urutan Bessel
p dalam bentuk:
z2 fracd2wdz2+z fracdwdz+(z2−p2)w=0,(1)
dan gantikan di sini
w=x− alpha,z=kx beta,(2)
Kemudian, menggunakan (2) dan memperkenalkan konstanta
A,B,C dari persamaan (1), kita memperoleh:
x2y″+Axey′+(B+Cxq)y=0,(3)
A=1−2 alpha,B= alpha2− beta2p2,C= beta2k2,q=2 beta,(4)
Dari persamaan (4) kita dapatkan:
\ left \ {\ begin {matrix} \ alpha = \ frac {1-A} {2}, \\ \ beta = \ frac {q} {2}, \\ k = \ frac {2 \ sqrt {C }} {q} \\ p = \ frac {\ sqrt {(1-A ^ {2} -4B}} {q} \\ \ end {matrix} \ kanan. (5)
Jika
C>0 ,
q neq0 ,
(1−A)2 geqslant4B , maka solusi umum (untuk
x>0 ) dari persamaan (3) memiliki bentuk:
y(x)=x alpha kiri[c1Jp(kx beta)+c2J−p(kx beta) kanan](6)
dimana:
alpha ,
beta ,
k ditentukan dari sistem (5). Jika
p Adalah bilangan bulat kalau begitu
Jp perlu diganti oleh
Yp .
Pembengkokan longitudinal pada kolom vertikalKami sekarang akan mempertimbangkan tugas yang penting untuk aplikasi praktis. Dalam tugas ini, diperlukan untuk menentukan kapan kolom vertikal yang seragam ditekuk di bawah bobotnya sendiri. Kami kira
x=0 di ujung atas kolom dan
x=L>0 di dasarnya; kita asumsikan bahwa alasnya dimasukkan dengan kaku (mis., tidak bergerak) ke dalam alas (ke tanah), mungkin ke dalam beton.
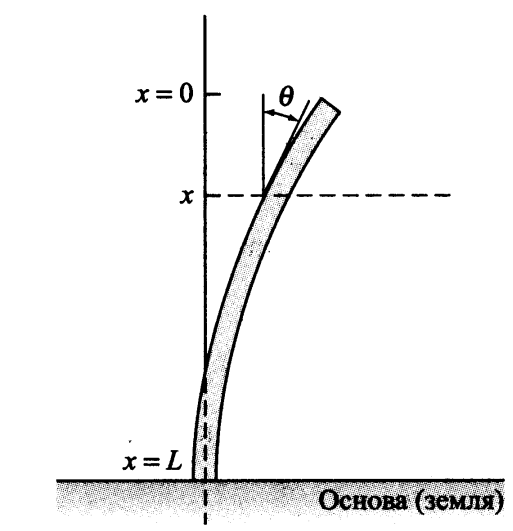
Nyatakan deviasi sudut kolom pada titik tersebut
x melalui
theta(x) . Dari teori elastisitas dalam kondisi-kondisi ini dapat disimpulkan bahwa:
EI fracd2 thetadx2+g rhox theta=0,(7)
dimana
E - Modulus Young dari bahan kolom,
I - momen inersia dari penampang melintang,
rho - Kerapatan linear kolom dan
g - percepatan gravitasi. Kondisi batas adalah dalam bentuk:
theta′(0)=0, theta(L)=0,(8)
Kami akan memecahkan masalah menggunakan (7) dan (8) dengan:
lambda= gamma2= fracg rhoEI(9)
Kami menulis ulang (7) dengan mempertimbangkan (9) dalam kondisi (8):
fracd2 thetadx2+ gamma2x theta=0; fracd thetadx=0, theta(L)=0.(10)
Kolom dapat dideformasi hanya jika ada solusi non-sepele untuk masalah (10); jika tidak, kolom akan tetap pada posisi yang tidak menyimpang dari vertikal (mis., secara fisik tidak dapat menyimpang dari vertikal).
Persamaan diferensial (10) adalah persamaan Airy. Persamaan (10) memiliki bentuk persamaan (3) untuk
A=B=0 ,
C= gamma2 ,
q=3 . Dari sistem persamaan (5) kita dapatkan
alpha= frac12 ,
beta= frac32 ,
k= frac23 gamma ,
p= frac13 .
Oleh karena itu, solusi umum memiliki bentuk:
theta(x)=x1/2 kiri[c1J1/3( frac23 gammax3/2)+c2J−1/3( frac23 gammax3/2) kanan].(11)
Untuk menerapkan kondisi awal, kami mengganti
p= pm frac13 masuk
Jp= sum inftym=0 frac(−1)mm! Gamma(p+m+1) kiri( fracx2 kanan)2m+p(12)
Setelah transformasi (12), dengan mempertimbangkan solusi (11), kami memperoleh:
theta(x)= fracc1 gamma1/331/3 Gamma(4/3) kiri(x− frac gamma2x412+ frac gamma4x7504− cdot cdot cdot kanan)++ fracc231/3 gamma1/3 Gamma( frac23) kiri(1− frac gamma2x36+ frac gamma4x6180− cdot cdot cdot right).(13)
Disediakan di titik awal
theta′(0)=0 kita dapatkan
c1=0 , lalu (11) berbentuk:
theta(x)=c2x1/2J−1/3( frac23 gammax3/2),(14)
Disediakan pada titik akhir
theta(L)=0 , dari (14) kita dapatkan:
J−1/3( frac23 gammaL3/2)=0(15)
Perlu dicatat bahwa transformasi (13), (14) tidak dapat dilakukan jika grafik fungsi dibangun
J1/3(x),J−1/3(x) menggunakan kemampuan yang dipertimbangkan dari modul mpmath:
from mpmath import* mp.dps = 6; mp.pretty = True f=lambda x: besselj(-1/3,x) f1=lambda x: besselj(1/3,x) plot([f,f1], [0, 15])
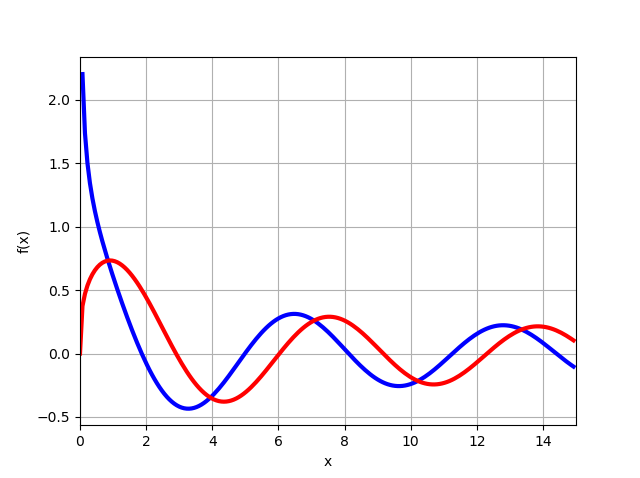
Dari grafik berikut bahwa untuk x = 0 fungsi
J1/3(0)=0 dan dengan mempertimbangkan solusi (11), kami segera mendapatkan persamaan yang diperlukan (15), tetap hanya untuk menemukan z, seperti yang akan ditunjukkan di bawah ini.
Dengan demikian, kolom hanya berubah bentuk jika
z= frac23 gammaL3/2 Apakah akar dari persamaan
J−1/3(z)=0 . Bangun sebuah fungsi
J−1/3(z) pada grafik terpisah:
from mpmath import* mp.dps = 6; mp.pretty = True f=lambda x: besselj(-1/3,x) plot(f, [0, 15])

Grafik menunjukkan bahwa root pertama sedikit kurang dari 2. Temukan root
z0 dari persamaan
J−1/3(z)=0 Anda dapat, menggunakan fungsi
findroot (f, z0) , menerima, sesuai dengan grafik, pencarian
x0=1 dan enam tempat desimal
mp.dps = 6 :
from mpmath import* mp.dps = 6; mp.pretty = True f=lambda x: besselj(-1/3,x) print("z0=%s"%findroot(f, 1)
Kami mendapatkan:
z0=1.86635Kami menghitung panjang kritis, misalnya, tiang bendera, menggunakan rumus (15):
Tinggi tiang bendera untuk parameter yang berbeda di bagian from numpy import* def LRr(R,r): E=2.9*10**11
Kami mendapatkan:
8,47 m
10,25 m
Tiang bendera berlubang mungkin lebih tinggi dari yang solid.
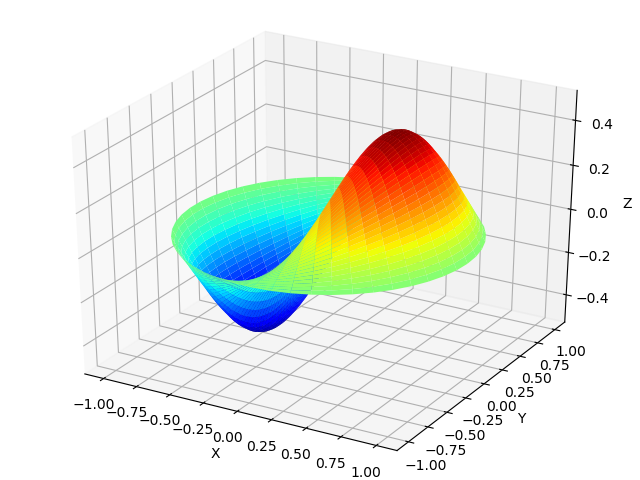
Perambatan gelombang dalam membran tipis.
Selaput tipis ketika gelombang suara masuk tidak hanya berosilasi dengan frekuensi gelombang. Bentuk getaran membran dapat diperoleh dalam fungsi Bessel sesuai dengan daftar berikut, menggunakan rumus
besselj () dan
besseljzero () :
Gelombang Membran from mpmath import* from numpy import* import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D from matplotlib import cm def Membrana(r): mp.dps=25 return cos(0.5) * cos( theta) *float(besselj(1,r*besseljzero(1,1) ,0)) theta =linspace(0,2*pi,50) radius = linspace(0,1,50) x = array([r * cos(theta) for r in radius]) y = array([r * sin(theta) for r in radius]) z = array([Membrana(r) for r in radius]) fig = plt.figure("") ax = Axes3D(fig) ax.plot_surface(x, y, z, rstride=1, cstride=1, cmap=cm.jet) ax.set_xlabel('X') ax.set_ylabel('Y') ax.set_zlabel('Z') plt.show()
Alternatif untuk modul mpmath dalam fungsi Bessel khusus dari perpustakaan SciPy
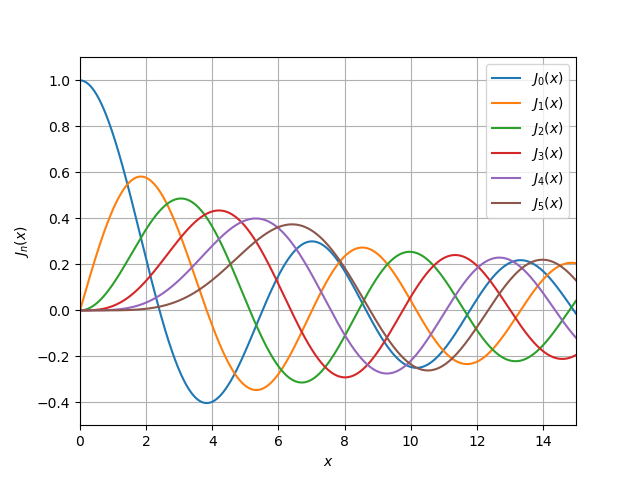
Tanpa menggali diskusi rinci tentang fungsi Bessel dari perpustakaan SciPy [4], saya hanya akan memberikan dua daftar untuk fungsi plot dari jenis pertama dan kedua
jv (v, x) ,
yv (v, x) :
jv (v, x) import numpy as np import pylab as py import scipy.special as sp x = np.linspace(0, 15, 500000) for v in range(0, 6): py.plot(x, sp.jv(v, x)) py.xlim((0, 15)) py.ylim((-0.5, 1.1)) py.legend(('$J_{0}(x)$', '$ J_{1}(x)$', '$J_{2}(x)$', '$J_{3}(x)$', '$ J_{4}(x)$','$ J_{5}(x)$'), loc = 0) py.xlabel('$x$') py.ylabel('${J}_n(x)$') py.grid(True) py.show()
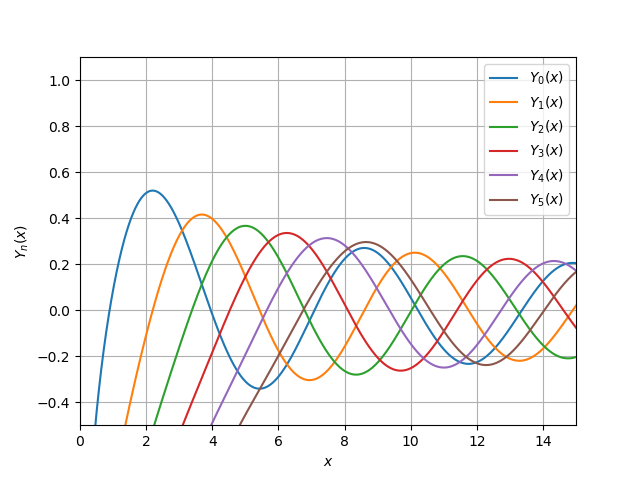
yv (v, x) import numpy as np import pylab as py import scipy.special as sp x = np.linspace(0, 15, 500000) for v in range(0, 6): py.plot(x, sp.yv(v, x)) py.xlim((0, 15)) py.ylim((-0.5, 1.1)) py.legend(('$Y_{0}(x)$', '$ Y_{1}(x)$', '$Y_{2}(x)$', '$Y_{3}(x)$', '$ Y_{4}(x)$','$ Y_{5}(x)$'), loc = 0) py.xlabel('$x$') py.ylabel('$Y_{n}(x)$') py.grid(True) py.show()
Kesimpulan:
Artikel ini menjelaskan dasar-dasar bekerja dengan fungsi Bessel menggunakan pustaka mpmath, sympy, dan scipy, memberikan contoh penggunaan fungsi untuk menyelesaikan persamaan diferensial. Artikel ini mungkin berguna dalam mempelajari persamaan fisika matematika.
Referensi:
1.
Fungsi Bessel2.
Menggunakan transformasi Laplace terbalik untuk menganalisis tautan dinamis sistem kontrol3.
Fungsi terkait fungsi Bessel4.
Fungsi khusus (scipy.special).