Salah satu legenda urban mengatakan bahwa pencipta tas gula, tongkat, gantung diri ketika mengetahui bahwa konsumen tidak memecahkannya menjadi dua di atas cangkir, tetapi dengan lembut merobek ujungnya. Ini, tentu saja, tidak demikian, tetapi jika logika ini diikuti, maka seorang pecinta bir Guinness Inggris bernama William Gosset seharusnya tidak hanya menggantung diri, tetapi dengan perputarannya di peti mati seharusnya sudah mengebor Bumi ke pusat. Dan semua karena penemuan ikoniknya, yang diterbitkan di bawah nama samaran Student , telah disalahgunakan secara buruk selama beberapa dekade.
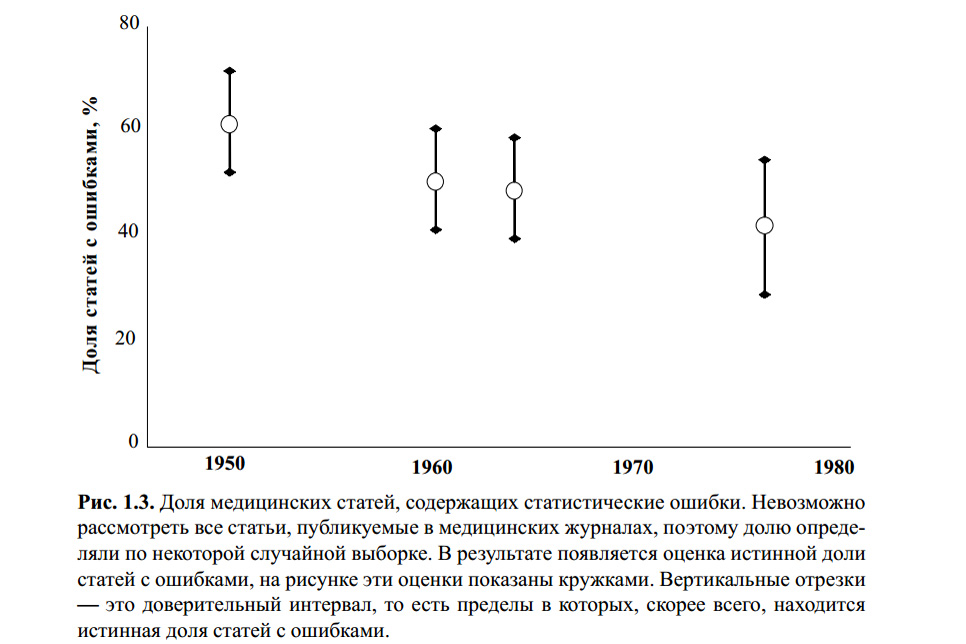
Gambar di atas adalah dari buku S. Glanz. Statistik biomedis. Per. dari bahasa inggris - M., Praktek, 1998 .-- 459 hal. Saya tidak tahu apakah ada yang memeriksa kesalahan statistik perhitungan untuk grafik ini. Namun, sejumlah artikel modern tentang topik ini, dan pengalaman saya sendiri menunjukkan bahwa kriteria Student-T tetap yang paling terkenal, dan karena itu yang paling populer digunakan, dengan atau tanpa.
Alasan untuk ini adalah pendidikan dangkal (guru ketat mengajarkan bahwa Anda perlu "memeriksa statistik", jika tidak uuuuuu!), Kemudahan penggunaan (tabel dan kalkulator online tersedia dalam banyak) dan keengganan dangkal untuk menggali fakta bahwa "dan itu berfungsi." Kebanyakan orang yang telah menggunakan kriteria ini setidaknya sekali dalam makalah mereka atau bahkan karya ilmiah akan mengatakan sesuatu seperti: "Ya, kami membandingkan 5 anak sekolah yang marah dan 7 anak sekolah yang gamer dalam hal agresi, nilai tabel kami mendekati p = 0,05 dan ini berarti game itu jahat. Ya, tidak persis, tetapi dengan probabilitas 95%. " Berapa banyak kesalahan logis dan metodologis yang telah mereka buat?
Dasar-dasarnya
Berdasarkan apa uji-t siswa? Logikanya diambil dari teorema Bayesian, dasar matematika dari distribusi Gaussian, metodologi ini didasarkan pada analisis varian:

di mana parameter μ adalah ekspektasi matematis (nilai rata-rata) dari distribusi, dan parameter σ adalah standar deviasi (σ ² adalah varian) dari distribusi.
Apa itu analisis varian? Bayangkan audiens Habr, diurutkan berdasarkan jumlah orang dari setiap usia tertentu. Jumlah orang berdasarkan usia cenderung mematuhi distribusi normal - sesuai dengan fungsi Gauss:
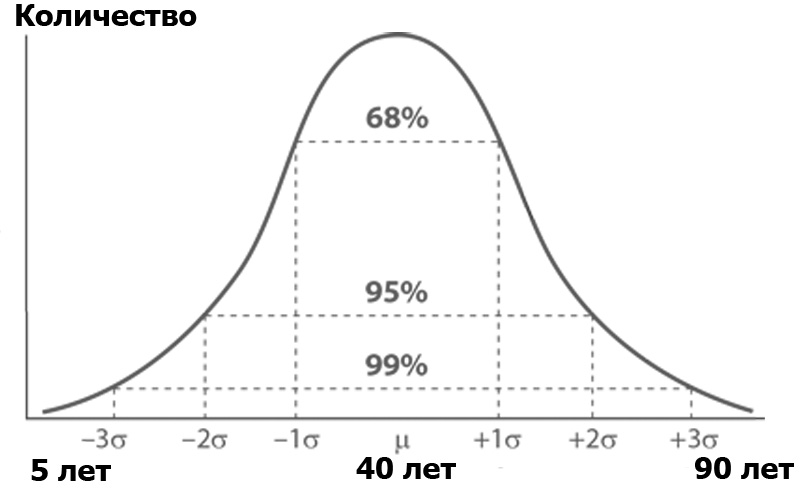
Distribusi normal memiliki properti yang menarik - hampir semua nilainya terletak pada batas tiga standar deviasi dari nilai rata-rata. Dan apa standar deviasi? Ini adalah akar dari varian. Dispersi , pada gilirannya, adalah jumlah kuadrat dari perbedaan semua anggota populasi umum dan nilai rata-rata dibagi dengan jumlah anggota ini:
Artinya, setiap nilai dikurangi dari rata-rata, kuadrat untuk membunuh minus, dan kemudian mengambil rata-rata, dengan bodohnya disimpulkan dan dibagi dengan jumlah nilai-nilai ini. Hasilnya adalah ukuran dispersi rata-rata nilai relatif terhadap varians rata-rata.
Bayangkan bahwa kami memilih dua sampel dalam populasi umum ini: pembaca hub Cryptocurrency dan pembaca hub Old Iron. Dengan membuat sampel acak , kami selalu mendapatkan distribusi mendekati normal . Dan sekarang kami mendapatkan distributor kecil di dalam populasi kami:
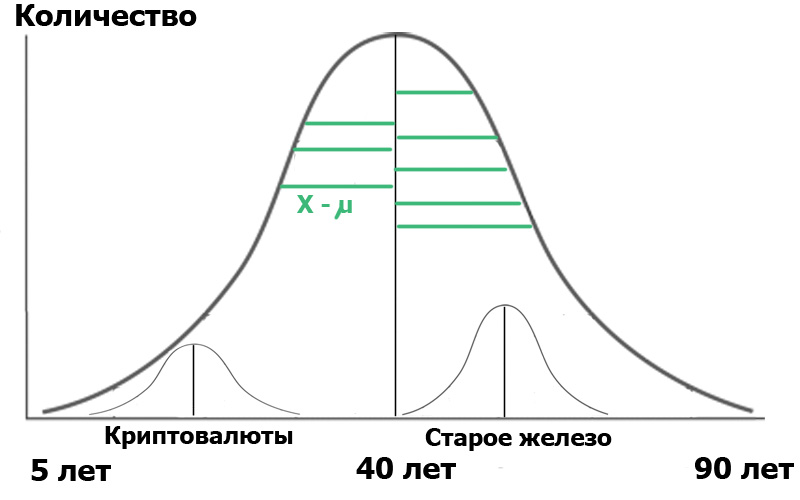
Untuk kejelasan, saya menunjukkan segmen hijau - jarak dari titik distribusi ke nilai rata-rata. Jika panjang segmen hijau ini dikuadratkan, dijumlahkan, dan dirata-rata - ini akan menjadi varian.
Dan sekarang - perhatian. Kita dapat mengkarakterisasi populasi melalui dua sampel kecil ini. Di satu sisi, varians dari sampel mencirikan varians dari seluruh populasi. Di sisi lain, nilai rata-rata sampel itu sendiri juga angka-angka yang variansnya dapat dihitung! Jadi: kami memiliki rata - rata varian sampel dan varian nilai rata-rata sampel.
Kemudian kita dapat melakukan analisis varian, secara kasar merepresentasikannya dalam bentuk rumus logis:
Apa yang akan diberikan formula di atas kepada kita? Sangat sederhana. Dalam statistik, semuanya dimulai dengan "hipotesis nol", yang dapat dirumuskan sebagai "tampaknya bagi kita", "semua kebetulan adalah acak" - dalam arti, dan "tidak ada hubungan antara dua peristiwa yang diamati" - jika benar-benar. Jadi, dalam kasus kami, hipotesis nol adalah tidak adanya perbedaan yang signifikan antara distribusi usia pengguna kami di dua hub. Dalam kasus hipotesis nol, diagram kita akan terlihat seperti ini:
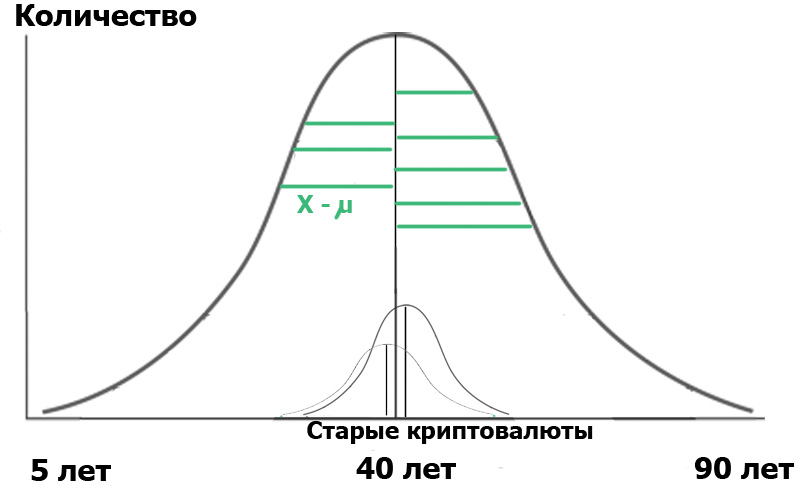
Ini berarti bahwa kedua varian sampel dan nilai rata-ratanya sangat dekat atau sama satu sama lain, dan oleh karena itu, secara umum, kriteria kami
Tetapi jika varians sampel sama, tetapi usia habrausers benar-benar sangat berbeda, maka pembilangnya (varians dari nilai rata-rata) akan besar, dan F akan jauh lebih dari satu. Maka diagram akan terlihat lebih seperti pada gambar sebelumnya. Dan apa yang akan memberi kita? Tidak ada, jika Anda tidak memperhatikan kata-katanya: hipotesis nol adalah tidak adanya perbedaan yang signifikan .
Tapi signifikansinya ... kita atur sendiri. Ini dilambangkan sebagai α dan memiliki arti sebagai berikut: tingkat signifikansi adalah probabilitas maksimum yang dapat diterima untuk menolak hipotesis nol secara keliru . Dengan kata lain, kami akan menganggap acara kami sebagai perbedaan yang signifikan antara satu kelompok dan yang lain, hanya jika probabilitas P dari kesalahan kami kurang dari α. Ini adalah p terkenal <0,05, karena biasanya dalam penelitian biomedis tingkat signifikansi ditetapkan pada 5%.
Nah, maka semuanya sederhana. Bergantung pada α, ada nilai kritis F, dimulai dengan mana kami menolak hipotesis nol. Mereka diterbitkan dalam bentuk tabel, yang sudah biasa kita gunakan. Ini untuk analisis varians. Dan bagaimana dengan siswa itu?
Begitu kata si Pelajar
Dan kriteria siswa hanyalah kasus khusus dari analisis varian. Sekali lagi, saya tidak akan membebani Anda dengan rumus yang mudah google, tapi saya akan sampaikan intinya:
Jadi, semua penjelasan panjang ini harus sangat kasar dan lancar, tetapi jelas menunjukkan berdasarkan apa kriteria tersebut. Dan karenanya, dari apa sifat bawaannya secara langsung mengikuti batasan penggunaannya, yang bahkan oleh para ilmuwan profesional sekalipun sering membuat kesalahan.
Properti Satu: Normalitas Distribusi.
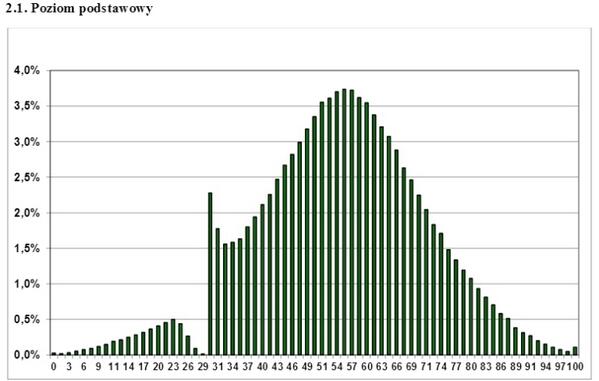
Ini adalah beberapa tahun sebagai grafik distribusi skor ujian negara Polandia di Internet. Kesimpulan apa yang bisa ditarik darinya? Bahwa ujian ini tidak lulus hanya benar-benar jijik Gopnik? Apa guru "mencapai" siswa? Tidak, hanya satu - untuk distribusi selain normal, Anda tidak dapat menerapkan kriteria analisis parametrik, seperti Siswa. Jika Anda memiliki grafik distribusi satu sisi, bergerigi, bergelombang, diskrit - lupakan kriteria-t, Anda tidak dapat menggunakannya. Namun, ini terkadang berhasil diabaikan bahkan oleh karya ilmiah yang serius.
Apa yang harus dilakukan dalam kasus ini? Gunakan apa yang disebut kriteria analisis nonparametrik. Mereka menerapkan pendekatan yang berbeda, yaitu menentukan peringkat data, yaitu menjauh dari nilai-nilai dari masing-masing poin ke peringkat yang ditugaskan padanya. Kriteria ini kurang akurat daripada yang parametrik, tetapi setidaknya penggunaannya benar, berbeda dengan penggunaan kriteria parametrik yang tidak dibenarkan pada populasi abnormal. Dari kriteria ini, kriteria U-Mann Whitney paling dikenal, dan sering digunakan sebagai kriteria "untuk sampel kecil." Ya, ini memungkinkan Anda untuk menangani sampel hingga 5 poin, tetapi ini, sebagaimana seharusnya sudah jelas, bukan tujuan utamanya.
Properti kedua: apakah Anda ingat rumusnya? Nilai-nilai kriteria-F berubah dengan perbedaan (peningkatan varians) dari nilai rata - rata sampel . Tetapi penyebutnya, yaitu varians itu sendiri, tidak boleh berubah. Oleh karena itu, kriteria lain untuk penerapan harus kesetaraan varian. Fakta bahwa pemeriksaan ini diamati bahkan lebih jarang dikatakan, misalnya, di sini: Kesalahan dalam analisis statistik data biomedis. Leonov V.P. Jurnal Internasional Praktik Kedokteran, 2007, no. 2, hlm . 19-35 .
Properti Tiga: Perbandingan dua sampel. Mereka suka menggunakan kriteria-t untuk membandingkan lebih dari dua kelompok. Sebagai aturan, ini dilakukan sebagai berikut: perbedaan antara kelompok A dari B, B dari C, dan A dari C. dibandingkan secara berpasangan.Kemudian, berdasarkan ini, kesimpulan tertentu dibuat, yang sama sekali tidak benar. Dalam hal ini, efek dari beberapa perbandingan muncul.
Setelah memperoleh nilai t yang cukup tinggi di salah satu dari tiga perbandingan, para peneliti melaporkan bahwa "P <0,05". Tetapi pada kenyataannya, probabilitas kesalahan secara signifikan melebihi 5%.
Mengapa
Kami mencari tahu: misalnya, penelitian ini mengadopsi tingkat signifikansi 5%. Ini berarti bahwa probabilitas maksimum yang dapat diterima untuk menolak hipotesis nol secara keliru ketika membandingkan kelompok A dan B adalah 5%. Tampaknya semuanya benar? Tetapi kesalahan yang sama persis akan terjadi dalam kasus membandingkan kelompok B dan C, dan ketika membandingkan kelompok A dan C juga. Akibatnya, kemungkinan melakukan kesalahan secara keseluruhan dengan penilaian semacam ini tidak akan menjadi 5%, tetapi lebih dari itu. Secara umum, probabilitas ini sama dengan
P ′ = 1 - (1 - 0,05) ^ k
di mana k adalah jumlah perbandingan.
Kemudian, dalam penelitian kami, probabilitas membuat kesalahan dalam menolak hipotesis nol adalah sekitar 15%. Ketika membandingkan empat kelompok, jumlah pasangan dan, karenanya, kemungkinan perbandingan berpasangan adalah 6. Oleh karena itu, dengan tingkat signifikansi dalam masing-masing perbandingan 0,05
probabilitas salah mendeteksi perbedaan setidaknya satu tidak lagi 0,05, tetapi 0,31.
Meski demikian, kesalahan ini tidak sulit dihilangkan. Salah satu caranya adalah memperkenalkan amandemen Bonferroni. Ketimpangan Bonferroni memberi tahu kami bahwa jika Anda menerapkan kriteria k kali
dengan tingkat signifikansi α, maka probabilitas, setidaknya dalam satu kasus, untuk menemukan perbedaan di mana tidak ada tidak melebihi produk k oleh α. Dari sini:
α ′ <αk,
di mana α ′ adalah probabilitas setidaknya sekali salah mengira perbedaannya. Maka masalah kita diselesaikan dengan sangat sederhana: kita perlu membagi tingkat signifikansi kita dengan koreksi Bonferroni - yaitu, dengan banyaknya perbandingan. Untuk tiga perbandingan, kita perlu mengambil nilai yang sesuai dengan α = 0,05 / 3 = 0,0167 dari tabel uji-t. Saya ulangi - ini sangat sederhana, tetapi amandemen ini tidak dapat diabaikan. Ngomong-ngomong, Anda tidak boleh terbawa oleh amandemen ini, bahkan setelah membaginya dengan angka 8, nilai-nilai kriteria-t lebih ketat.
Berikutnya "hal-hal kecil" yang sangat sering mereka tidak perhatikan sama sekali. Saya sengaja tidak memberikan rumus di sini, agar tidak mengurangi keterbacaan teks, tetapi harus diingat bahwa perhitungan kriteria-t bervariasi untuk kasus-kasus berikut:
Ukuran berbeda dari dua sampel (secara umum, ingat bahwa dalam kasus umum kami membandingkan dua kelompok menggunakan rumus untuk kriteria dua sampel);
Ketersediaan sampel tergantung. Ini adalah kasus ketika data diukur dari satu pasien pada interval waktu yang berbeda, data dari sekelompok hewan sebelum dan sesudah percobaan, dll.
Akhirnya, agar Anda dapat membayangkan sepenuhnya apa yang terjadi, saya akan memberikan data yang lebih baru tentang penggunaan kriteria-t yang salah. Jumlahnya untuk 1998 dan 2008 untuk sejumlah jurnal ilmiah Cina, dan mereka berbicara sendiri. Saya benar-benar ingin ini menjadi lebih ceroboh dalam desain daripada data ilmiah yang tidak akurat:
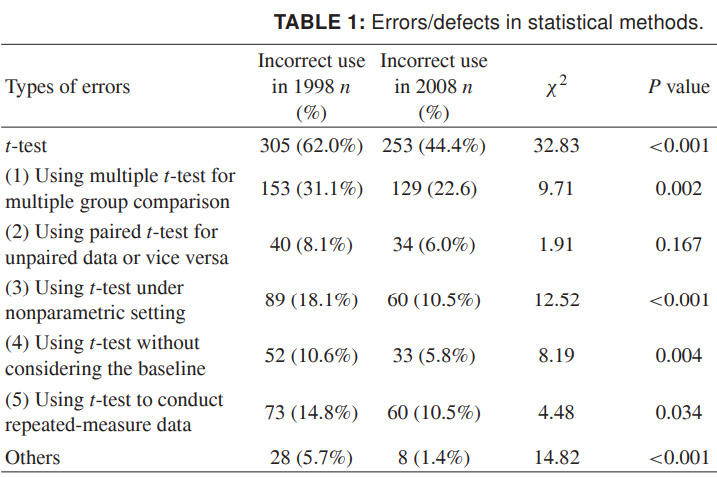
Sumber: Penyalahgunaan Metode Statistik dalam 10 Jurnal Medis Tiongkok Terkemuka pada tahun 1998 dan 2008. Shunquan Wu et al, The Scientific World Journal, 2011, 11, 2106–2114
Ingat, signifikansi rendah dari hasil bukanlah hal yang menyedihkan sebagai hasil yang salah. Tidak mungkin membawa dosa ilmiah - kesimpulan yang salah - dengan mendistorsi data dengan statistik yang salah diterapkan.
Tentang interpretasi logis, termasuk data statistik yang salah, saya, mungkin, akan memberi tahu secara terpisah.
Baca dengan benar.