Mountain Car: Memecahkan tantangan klasik dengan pelatihan penguatan

Sebagai aturan, modifikasi pada algoritma yang mengandalkan fitur spesifik dari tugas tertentu dianggap kurang bernilai, karena sulit untuk digeneralisasi ke kelas masalah yang lebih luas. Namun, ini tidak berarti modifikasi seperti itu tidak diperlukan. Selain itu, seringkali mereka dapat secara signifikan meningkatkan hasil bahkan untuk masalah klasik sederhana, yang sangat penting dalam aplikasi praktis algoritma. Sebagai contoh, dalam posting ini saya akan memecahkan masalah Mobil Gunung menggunakan pelatihan penguatan dan menunjukkan bahwa menggunakan pengetahuan tentang bagaimana tugas ini diatur, itu dapat diselesaikan lebih cepat.

Tentang diri saya

Nama saya Oleg Svidchenko, sekarang saya belajar di Sekolah Ilmu Fisika, Matematika dan Komputer St. Petersburg HSE, sebelum itu saya belajar di Universitas St. Petersburg selama tiga tahun. Saya juga bekerja di JetBrains Research sebagai peneliti. Sebelum memasuki universitas, saya belajar di SSC Moscow State University dan menjadi pemenang Olimpiade All-Rusia anak sekolah dalam ilmu komputer sebagai bagian dari tim Moskow.

Apa yang kita butuhkan

Jika Anda tertarik untuk mencoba pelatihan penguatan, tantangan Mobil Gunung sangat bagus untuk ini. Hari ini kita membutuhkan Python dengan pustaka Gym dan PyTorch yang terinstal , serta pengetahuan dasar jaringan saraf.

Deskripsi tugas

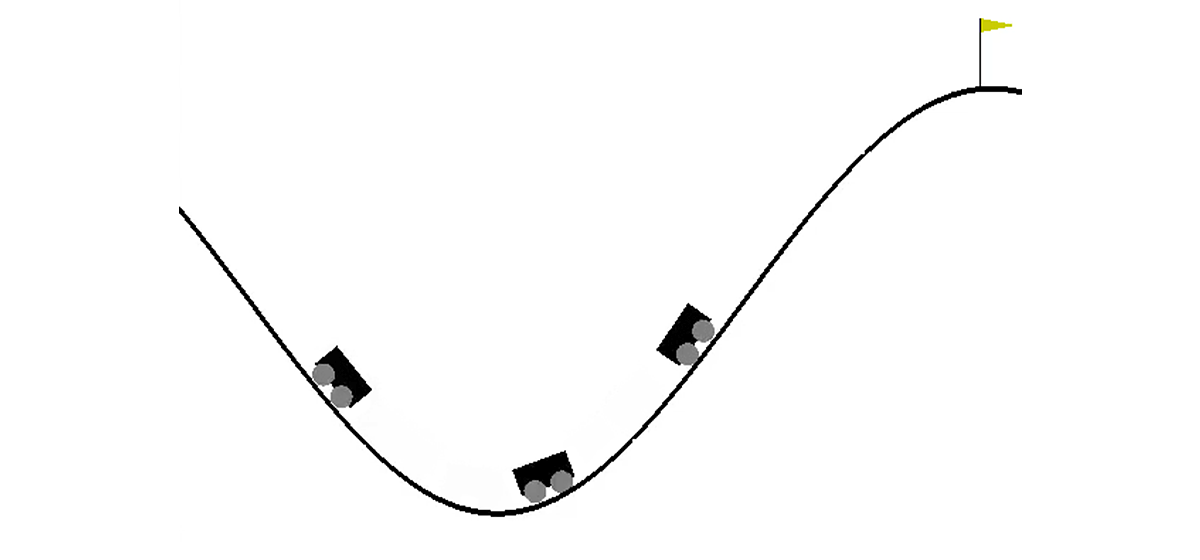
Dalam dunia dua dimensi, mobil harus memanjat dari lubang di antara dua bukit ke puncak bukit yang tepat. Ini rumit oleh kenyataan bahwa dia tidak memiliki tenaga mesin yang cukup untuk mengatasi kekuatan gravitasi dan masuk ke sana pada upaya pertama. Kami diundang untuk melatih agen (dalam kasus kami, jaringan saraf), yang dapat, dengan mengendalikannya, memanjat bukit kanan secepat mungkin.

Kontrol mesin dilakukan melalui interaksi dengan lingkungan. Ini dibagi menjadi episode independen, dan setiap episode dilakukan langkah demi langkah. Pada setiap langkah, agen menerima keadaan dan lingkungan r dari lingkungan sebagai respons atas tindakan a . Selain itu, kadang-kadang media juga dapat melaporkan bahwa episode telah berakhir. Dalam masalah ini, s adalah sepasang angka, yang pertama adalah posisi mobil pada kurva (satu koordinat sudah cukup, karena kita tidak dapat melepaskan diri dari permukaan), dan yang kedua adalah kecepatannya di permukaan (dengan tanda). Hadiah r adalah angka yang selalu sama dengan -1 untuk tugas ini. Dengan cara ini, kami mendorong agen untuk menyelesaikan episode secepat mungkin. Hanya ada tiga tindakan yang mungkin: dorong mobil ke kiri, jangan lakukan apa-apa dan dorong mobil ke kanan. Tindakan ini sesuai dengan angka dari 0 hingga 2. Episode dapat berakhir jika mobil mencapai puncak bukit yang tepat atau jika agen telah mengambil 200 langkah.

Sedikit teori

Pada Habré sudah ada artikel tentang DQN di mana penulis cukup baik menggambarkan semua teori yang diperlukan. Namun demikian, untuk kemudahan membaca, saya akan mengulanginya di sini dalam bentuk yang lebih formal.

Tugas pembelajaran penguatan didefinisikan oleh seperangkat ruang keadaan S, ruang tindakan A, koefisien $$$\ gamma$, fungsi transisi T dan fungsi hadiah R. Secara umum, fungsi transisi dan fungsi hadiah bisa menjadi variabel acak, tetapi sekarang kami akan mempertimbangkan versi yang lebih sederhana di mana mereka didefinisikan secara unik. Tujuannya adalah untuk memaksimalkan imbalan kumulatif. $$$\ sum_ {t = 0} ^ {T} r_ {t} \ cdot \ gamma ^ {t}$, di mana t adalah nomor langkah dalam medium, dan T adalah jumlah langkah dalam episode.

Untuk mengatasi masalah ini, kami mendefinisikan nilai-fungsi V negara s sebagai nilai maksimum hadiah kumulatif, asalkan kita mulai dalam keadaan s. Mengetahui fungsi seperti itu, kita dapat memecahkan masalah hanya dengan melewati di setiap langkah ke s dengan nilai maksimum yang mungkin. Namun, tidak semuanya begitu sederhana: dalam banyak kasus kita tidak tahu tindakan apa yang akan membawa kita ke keadaan yang diinginkan. Oleh karena itu, kami menambahkan aksi sebagai parameter kedua dari fungsi. Fungsi yang dihasilkan disebut fungsi-Q. Ini menunjukkan berapa banyak hadiah kumulatif maksimum yang bisa kita dapatkan dengan melakukan tindakan dalam keadaan s. Tapi kita sudah bisa menggunakan fungsi ini untuk menyelesaikan masalah: dalam keadaan s, kita cukup memilih sedemikian rupa sehingga Q (s, a) sudah maksimal.

Dalam praktiknya, kita tidak tahu fungsi-Q yang sebenarnya, tetapi kita dapat memperkirakannya dengan berbagai metode. Salah satu teknik tersebut adalah Deep Q Network (DQN). Idenya adalah bahwa untuk setiap tindakan kami memperkirakan fungsi-Q menggunakan jaringan saraf.

Lingkungan

Sekarang mari kita berlatih. Pertama, kita perlu belajar bagaimana meniru lingkungan MountainCar. Perpustakaan Gym, yang menyediakan sejumlah besar lingkungan pembelajaran penguatan standar, akan membantu kami mengatasi tugas ini. Untuk membuat sebuah lingkungan, kita perlu memanggil metode make pada modul gym yang meneruskannya dengan nama lingkungan yang diinginkan sebagai parameter:

import gym env = gym.make("MountainCar-v0") 

Dokumentasi terperinci dapat ditemukan di sini , dan deskripsi lingkungan ada di sini .
Mari kita pertimbangkan secara lebih terperinci apa yang dapat kita lakukan dengan lingkungan yang kita buat:

• env.reset() - mengakhiri episode saat ini dan memulai episode baru. Mengembalikan status awal.
• env.step(action) - melakukan tindakan yang ditentukan. Mengembalikan status baru, hadiah, apakah episode telah berakhir dan informasi tambahan yang dapat digunakan untuk debugging.
• env.seed(seed) - mengatur benih acak. Itu tergantung pada bagaimana status awal akan dihasilkan selama env.reset ().
• env.render() - menampilkan kondisi lingkungan saat ini.

Kami menyadari DQN

DQN adalah algoritma yang menggunakan jaringan saraf untuk mengevaluasi fungsi-Q. Dalam artikel aslinya, DeepMind mendefinisikan arsitektur standar untuk game Atari menggunakan jaringan saraf convolutional. Tidak seperti game ini, Mountain Car tidak menggunakan gambar sebagai keadaan, jadi kita harus menentukan arsitekturnya sendiri.

Ambil contoh, sebuah arsitektur dengan dua lapisan tersembunyi dari 32 neuron di masing-masingnya. Setelah setiap lapisan tersembunyi, kami akan menggunakan ReLU sebagai fungsi aktivasi. Dua angka yang menggambarkan status dimasukkan ke input dari jaringan saraf, dan pada output kita mendapatkan estimasi fungsi-Q.

 import torch.nn as nn model = nn.Sequential( nn.Linear(2, 32), nn.ReLU(), nn.Linear(32, 32), nn.ReLU(), nn.Linear(32, 3) ) target_model = copy.deepcopy(model) #    def init_weights(layer): if type(layer) == nn.Linear: nn.init.xavier_normal(layer.weight) model.apply(init_weights) 

Karena kita akan melatih jaringan saraf pada GPU, kita perlu memuat jaringan kita di sana:

 #     CPU,  “cuda”    “cpu” device = torch.device("cuda") model.to(device) target_model.to(device) 

Variabel perangkat akan bersifat global, karena kita juga perlu memuat data.

Kita juga perlu mendefinisikan optimizer yang akan memperbarui bobot model menggunakan gradient descent. Ya, ada banyak lebih dari satu.

 optimizer = optim.Adam(model.parameters(), lr=0.00003) 

Sekarang kita mendeklarasikan fungsi yang akan mempertimbangkan fungsi kesalahan, gradien sepanjang itu, dan menerapkan keturunan. Tetapi sebelum itu, Anda perlu mengunduh data dari batch ke GPU:

 state, action, reward, next_state, done = batch #       state = torch.tensor(state).to(device).float() next_state = torch.tensor(next_state).to(device).float() reward = torch.tensor(reward).to(device).float() action = torch.tensor(action).to(device) done = torch.tensor(done).to(device) 

Selanjutnya, kita perlu menghitung nilai sebenarnya dari fungsi-Q, namun, karena kita tidak mengetahuinya, kita akan mengevaluasinya melalui nilai-nilai untuk keadaan berikut:

 target_q = torch.zeros(reward.size()[0]).float().to(device) with torch.no_grad(): #     Q-function    target_q = target_model(next_state).max(1)[0].view(-1) target_q[done] = 0 target_q = reward + target_q * gamma 

Dan prediksi saat ini:

 q = model(state).gather(1, action.unsqueeze(1)) 

Menggunakan target_q dan q, kami menghitung fungsi kerugian dan memperbarui model:

 loss = F.smooth_l1_loss(q, target_q.unsqueeze(1)) #      optimizer.zero_grad() #     loss.backward() #   . ,       for param in model.parameters(): param.grad.data.clamp_(-1, 1) #    optimizer.step() 

Karena model hanya mempertimbangkan fungsi-Q, dan tidak melakukan tindakan, kita perlu menentukan fungsi yang akan memutuskan tindakan mana yang akan dilakukan agen. Sebagai algoritma pengambilan keputusan, kami ambil $$$\ varepsilon$politik -reedy. Idenya adalah bahwa agen biasanya melakukan tindakan dengan rakus, memilih fungsi-Q maksimum, tetapi dengan probabilitas $$$\ varepsilon$dia akan mengambil tindakan acak. Diperlukan tindakan acak sehingga algoritme dapat memeriksa tindakan tersebut yang tidak akan dilakukan hanya dengan dipandu oleh kebijakan serakah - proses ini disebut eksplorasi.

 def select_action(state, epsilon, model): if random.random() < epsilon: return random.randint(0, 2) return model(torch.tensor(state).to(device).float().unsqueeze(0))[0].max(0)[1].view(1, 1).item() 

Karena kami menggunakan batch untuk melatih jaringan saraf, kami membutuhkan buffer di mana kami akan menyimpan pengalaman berinteraksi dengan lingkungan dan dari mana kami akan memilih batch:

 class Memory: def __init__(self, capacity): self.capacity = capacity self.memory = [] self.position = 0 def push(self, element): """    """ if len(self.memory) < self.capacity: self.memory.append(None) self.memory[self.position] = element self.position = (self.position + 1) % self.capacity def sample(self, batch_size): """    """ return list(zip(*random.sample(self.memory, batch_size))) def __len__(self): return len(self.memory) 

Keputusan naif

Pertama, nyatakan konstanta yang akan kita gunakan dalam proses pembelajaran, dan buat model:

 #  model   target model target_update = 1000 #  ,      batch_size = 128 #   max_steps = 100001 #  exploration max_epsilon = 0.5 min_epsilon = 0.1 #    memory = Memory(5000) model, target_model, optimizer = create_new_model() 

Terlepas dari kenyataan bahwa akan logis untuk membagi proses interaksi menjadi beberapa episode, untuk menggambarkan proses pembelajaran, lebih mudah bagi kita untuk membaginya menjadi langkah-langkah terpisah, karena kami ingin membuat satu langkah penurunan gradien setelah setiap langkah lingkungan.

Mari kita bicara lebih terinci tentang bagaimana satu langkah pembelajaran terlihat seperti di sini. Kami berasumsi bahwa sekarang kami membuat langkah dengan jumlah langkah dari langkah max_steps dan status saat ini. Kemudian lakukan aksinya bersama $$$\ varepsilon$Kebijakan -reedy akan terlihat seperti ini:

 epsilon = max_epsilon - (max_epsilon - min_epsilon)* step / max_steps action = select_action(state, epsilon, model) new_state, reward, done, _ = env.step(action) 

Segera tambahkan pengalaman yang diperoleh ke memori dan mulai episode baru jika episode saat ini telah berakhir:

 memory.push((state, action, reward, new_state, done)) if done: state = env.reset() done = False else: state = new_state 

Dan kami akan mengambil langkah gradient descent (jika, tentu saja, kami sudah dapat mengumpulkan setidaknya satu batch):

 if step > batch_size: fit(memory.sample(batch_size), model, target_model, optimizer) 

Sekarang tetap memperbarui target_model:

 if step % target_update == 0: target_model = copy.deepcopy(model) 

Namun, kami juga ingin mengikuti proses pembelajaran. Untuk melakukan ini, kami akan memainkan episode tambahan setelah setiap pembaruan target_model dengan epsilon = 0, menyimpan total penghargaan di buffer rewards_by_target_updates:

 if step % target_update == 0: target_model = copy.deepcopy(model) state = env.reset() total_reward = 0 while not done: action = select_action(state, 0, target_model) state, reward, done, _ = env.step(action) total_reward += reward done = False state = env.reset() rewards_by_target_updates.append(total_reward) 

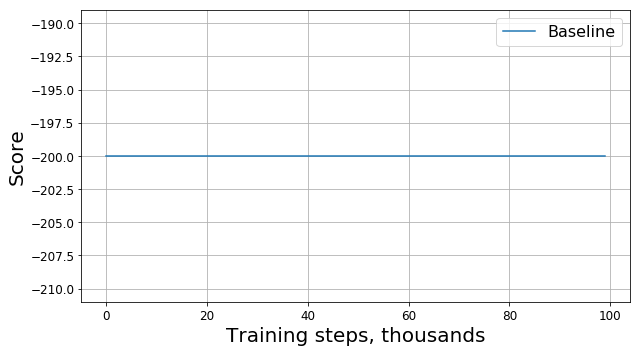
Jalankan kode ini dan dapatkan sesuatu seperti grafik ini:

Apa yang salah?

Apakah ini bug? Apakah ini algoritma yang salah? Apakah ini parameter buruk? Tidak juga. Padahal, masalahnya ada di tugas, yaitu pada fungsi hadiah. Mari kita lihat lebih dekat. Pada setiap langkah, agen kami menerima hadiah -1, dan ini terjadi hingga episode berakhir. Hadiah seperti itu memotivasi agen untuk menyelesaikan episode secepat mungkin, tetapi pada saat yang sama tidak memberitahunya bagaimana melakukannya. Karena itu, satu-satunya cara untuk belajar bagaimana menyelesaikan masalah dalam formulasi untuk agen adalah dengan menyelesaikannya berkali-kali menggunakan eksplorasi.

Tentu saja, orang dapat mencoba menggunakan algoritma yang lebih kompleks untuk mempelajari lingkungan daripada kita $$$\ varepsilon$Kebijakan -greedy. Namun, pertama, karena penerapannya, model kami akan menjadi lebih kompleks, yang ingin kami hindari, dan kedua, bukan fakta bahwa mereka akan bekerja cukup baik untuk tugas ini. Sebagai gantinya, kita dapat menghilangkan sumber masalah dengan memodifikasi tugas itu sendiri, yaitu dengan mengubah fungsi hadiah, yaitu dengan menerapkan apa yang disebut reward shaping.

Mempercepat konvergensi

Pengetahuan intuitif kami memberi tahu kami bahwa untuk mendaki bukit, Anda harus mempercepat. Semakin tinggi kecepatan, semakin dekat agen untuk memecahkan masalah. Anda dapat memberitahunya tentang ini, misalnya, dengan menambahkan modul kecepatan dengan koefisien tertentu pada hadiah:

  modified_reward = hadiah + 10 * abs (new_state [1]) 

Dengan demikian, garis dalam fungsi tersebut pas

  memory.push ((status, tindakan, hadiah, new_state, selesai)) 

harus diganti oleh

  memory.push ((status, aksi, modified_reward, new_state, selesai)) 

Sekarang mari kita lihat pada grafik baru (ini menyajikan penghargaan asli tanpa modifikasi):


Di sini RS adalah kependekan dari Reward Shaping.

Apakah baik melakukan ini?

Kemajuannya jelas: agen kami jelas belajar untuk mendaki bukit, karena penghargaan mulai berbeda dari -200. Hanya ada satu pertanyaan yang tersisa: jika mengubah fungsi hadiah, kami juga mengubah tugas itu sendiri, akankah solusi untuk masalah baru yang kami temukan baik untuk masalah lama?

Untuk memulainya, kita memahami apa artinya "kebaikan" dalam kasus kita. Menyelesaikan masalah, kami mencoba menemukan kebijakan yang optimal - kebijakan yang memaksimalkan total hadiah untuk episode tersebut. Dalam hal ini, kita dapat mengganti kata "baik" dengan kata "optimal", karena kita mencarinya. Kami juga optimis berharap bahwa cepat atau lambat DQN kami akan menemukan solusi optimal untuk masalah yang dimodifikasi, dan tidak terjebak pada maksimum lokal. Jadi, pertanyaannya dapat dirumuskan kembali sebagai berikut: jika mengubah fungsi hadiah, kami juga mengubah masalah itu sendiri, akankah solusi optimal untuk masalah baru yang kami temukan menjadi optimal untuk masalah yang lama?

Ternyata, kami tidak dapat memberikan jaminan seperti itu dalam kasus umum. Jawabannya tergantung pada bagaimana tepatnya kita mengubah fungsi hadiah, bagaimana itu diatur sebelumnya dan bagaimana lingkungan itu sendiri diatur. Untungnya, ada sebuah artikel yang penulisnya menyelidiki bagaimana mengubah fungsi hadiah mempengaruhi optimalitas solusi yang ditemukan.

Pertama, mereka menemukan seluruh kelas perubahan "aman" yang didasarkan pada metode potensial: $$$R ’= R + (\ gamma \ cdot \ Phi (new \ _state) - \ Phi (negara bagian))$dimana $$$\ Phi$- potensi, yang hanya bergantung pada negara. Untuk fungsi seperti itu, penulis dapat membuktikan bahwa jika solusi untuk masalah baru optimal, maka untuk masalah lama juga optimal.

Kedua, penulis menunjukkan itu untuk yang lain $$$R ’= R + F (s, a)$ada masalah seperti itu, fungsi hadiah R, dan solusi optimal untuk masalah yang diubah, bahwa solusi ini tidak optimal untuk masalah aslinya. Ini berarti bahwa kami tidak dapat menjamin kebaikan solusi yang kami temukan jika kami menggunakan perubahan yang tidak didasarkan pada metode potensial.

Dengan demikian, penggunaan fungsi potensial untuk memodifikasi fungsi hadiah hanya dapat mengubah tingkat konvergensi algoritma, tetapi tidak mempengaruhi solusi akhir.

Percepat konvergensi dengan benar

Sekarang kita tahu bagaimana cara mengubah hadiah dengan aman, mari kita coba modifikasi tugas lagi, menggunakan metode potensial alih-alih heuristik naif:

  modified_reward = hadiah + 300 * (gamma * abs (new_state [1]) - abs (status [1])) 

Mari kita lihat jadwal penghargaan asli:



Ternyata, selain memiliki jaminan teoretis, memodifikasi hadiah dengan bantuan fungsi potensial juga secara signifikan meningkatkan hasilnya, terutama pada tahap awal. Tentu saja, ada kemungkinan bahwa akan mungkin untuk memilih hiperparameter yang lebih optimal (benih acak, gamma, dan koefisien lainnya) untuk melatih agen, tetapi pembentukan hadiah namun secara signifikan meningkatkan laju konvergensi model.

Kata penutup

Terima kasih sudah membaca sampai akhir! Saya harap Anda menikmati perjalanan kecil berorientasi praktik ini ke dalam pembelajaran yang diperkuat. Jelas bahwa Mountain Car adalah tugas "mainan", namun, seperti yang dapat kami perhatikan, untuk mengajar agen memecahkan bahkan tugas yang tampaknya sederhana dari sudut pandang manusia bisa sulit.