Besar o

Catatan Terjemahan singkat, agak menceritakan kembali kata-kata Anda sendiri.
UPD: seperti disebutkan dalam komentar, contohnya tidak sempurna. Penulis tidak mencari solusi terbaik untuk masalah ini, tujuannya adalah untuk menjelaskan kompleksitas algoritma "di jari".

Notasi O besar diperlukan untuk menggambarkan kompleksitas algoritme. Untuk ini, konsep waktu digunakan. Topik itu menakutkan bagi banyak orang, programmer menghindari berbicara tentang "waktu urutan N" adalah hal yang umum.

Jika Anda dapat mengevaluasi kode dalam hal Big O, Anda kemungkinan besar dianggap sebagai "orang pintar." Dan kemungkinan besar Anda akan menjalani wawancara berikutnya. Anda tidak akan dihentikan oleh pertanyaan apakah mungkin untuk mengurangi kompleksitas sepotong kode menjadi n log n terhadap n ^ 2.

Struktur data

Pilihan struktur data tergantung pada tugas spesifik: pada jenis data dan algoritma untuk pemrosesan mereka. Berbagai struktur data (dalam. NET atau Java atau Elixir) dibuat untuk beberapa jenis algoritma.

Seringkali, memilih satu atau lain struktur, kami hanya menyalin solusi yang diterima secara umum. Dalam kebanyakan kasus, ini sudah cukup. Namun pada kenyataannya, tanpa memahami kompleksitas algoritma, kami tidak dapat membuat pilihan berdasarkan informasi. Topik struktur data hanya dapat diteruskan setelah kompleksitas algoritma.

Di sini kita hanya akan menggunakan array angka (seperti dalam wawancara). Contoh JavaScript.

Mari kita mulai dengan yang paling sederhana: O (1)

Ambil 5 nomor array:

const nums = [1,2,3,4,5]; 

Misalkan Anda perlu mendapatkan elemen pertama. Kami menggunakan indeks untuk ini:

 const nums = [1,2,3,4,5]; const firstNumber = nums[0]; 

Seberapa rumitkah algoritma ini? Kita dapat mengatakan: "sama sekali tidak rumit - cukup ambil elemen pertama dari array." Ini benar, tetapi lebih tepat untuk menggambarkan kompleksitas melalui jumlah operasi yang dilakukan untuk mencapai hasil, tergantung pada input ( operasi input).

Dengan kata lain: berapa banyak operasi akan meningkat seiring dengan meningkatnya parameter input.

Dalam contoh kita, ada 5 parameter input, karena ada 5 elemen dalam array. Untuk mendapatkan hasilnya, Anda perlu melakukan satu operasi (mengambil elemen dengan indeks). Berapa banyak operasi yang diperlukan jika ada 100 elemen dalam array? Atau 1000? Atau 100.000? Semua sama, hanya satu operasi yang diperlukan.

Yaitu: "satu operasi untuk semua data input yang mungkin" - O (1).

O (1) dapat dibaca sebagai "kompleksitas urutan 1" (urutan 1), atau "algoritma berjalan dalam waktu konstan / konstan" (waktu konstan).

Anda sudah menebak bahwa algoritma O (1) adalah yang paling efisien.

Iterasi dan "waktu pemesanan n": O (n)

Sekarang mari kita cari jumlah elemen-elemen dari array:

 const nums = [1,2,3,4,5]; let sum = 0; for(let num of nums){ sum += num; } 

Sekali lagi kami bertanya pada diri sendiri: berapa banyak operasi input yang kita butuhkan? Di sini Anda perlu memilah-milah semua elemen, yaitu operasi pada setiap elemen. Semakin besar array, semakin banyak operasi.

Menggunakan notasi O Besar: O (n), atau "kompleksitas urutan n (urutan n)". Juga, jenis algoritma ini disebut "linier" atau bahwa algoritme itu "skala linear".

Analisis

Bisakah kita membuat penjumlahan lebih efisien? Secara umum tidak. Dan jika kita tahu bahwa array dijamin mulai dari 1, disortir dan tidak memiliki celah? Kemudian kita bisa menerapkan rumus S = n (n + 1) / 2 (di mana n adalah elemen terakhir dari array):

 const sumContiguousArray = function(ary){ //get the last item const lastItem = ary[ary.length - 1]; //Gauss's trick return lastItem * (lastItem + 1) / 2; } const nums = [1,2,3,4,5]; const sumOfArray = sumContiguousArray(nums); 

Algoritma seperti itu jauh lebih efisien daripada O (n), apalagi, dieksekusi dalam "waktu konstan / konstan", yaitu. itu adalah O (1).

Bahkan, ada lebih dari satu operasi: Anda perlu mendapatkan panjang array, mendapatkan elemen terakhir, melakukan perkalian dan pembagian. Bukankah itu O (3) atau sesuatu? Dalam notasi O Besar, jumlah langkah aktual tidak penting, penting bahwa algoritma berjalan dalam waktu yang konstan.

Algoritma konstan-waktu selalu O (1). Sama dengan algoritma linier, pada kenyataannya, operasi dapat menjadi O (n + 5), dalam Big O notasi adalah O (n).

Bukan solusi terbaik: O (n ^ 2)

Mari kita menulis fungsi yang memeriksa array untuk duplikat. Solusi Nested Loop:

 const hasDuplicates = function (num) { //loop the list, our O(n) op for (let i = 0; i < nums.length; i++) { const thisNum = nums[i]; //loop the list again, the O(n^2) op for (let j = 0; j < nums.length; j++) { //make sure we're not checking same number if (j !== i) { const otherNum = nums[j]; //if there's an equal value, return if (otherNum === thisNum) return true; } } } //if we're here, no dups return false; } const nums = [1, 2, 3, 4, 5, 5]; hasDuplicates(nums);//true 

Kita sudah tahu bahwa iterasi array adalah O (n). Kami memiliki loop bersarang, untuk setiap elemen kami mengulangi lagi - yaitu O (n ^ 2) atau "kompleksitas urutan n kuadrat."

Algoritma dengan loop bersarang atas koleksi yang sama selalu O (n ^ 2).

"Kompleksitas urutan log n": O (log n)

Pada contoh di atas, loop bersarang, dengan sendirinya (jika Anda tidak memperhitungkannya bersarang), memiliki kompleksitas O (n), karena ini adalah enumerasi elemen array. Siklus ini berakhir segera setelah elemen yang diinginkan ditemukan, mis. pada kenyataannya, tidak semua elemen akan disebutkan. Namun notasi Big O selalu mempertimbangkan skenario terburuk - item yang Anda cari mungkin yang terakhir.

Di sini, loop bersarang digunakan untuk mencari elemen yang diberikan dalam array. Pencarian elemen dalam array, dalam kondisi tertentu, dapat dioptimalkan - dilakukan lebih baik daripada linear O (n).

Biarkan array diurutkan. Kemudian kita dapat menggunakan algoritma pencarian biner: membagi array menjadi dua bagian, membuang yang tidak perlu, membagi sisanya lagi menjadi dua bagian, dan seterusnya sampai kita menemukan nilai yang diinginkan. Jenis algoritma ini disebut Divide and Conquer Divide and Conquer.



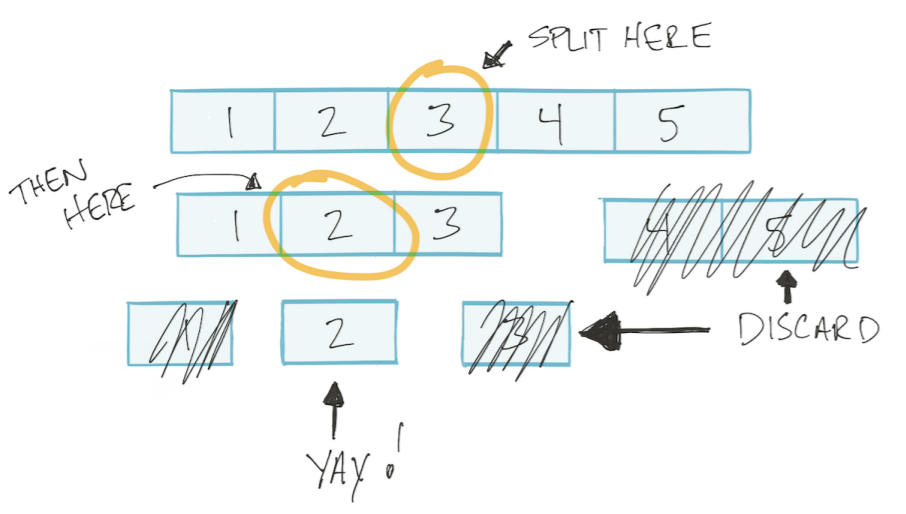
Algoritma ini didasarkan pada logaritma.

Tinjauan singkat logaritma

Pertimbangkan sebuah contoh, apa yang akan sama dengan x?

x ^ 3 = 8

Kita perlu mengambil akar kubik 8 - ini akan 2. Sekarang lebih sulit

2 ^ x = 512

Menggunakan logaritma, masalahnya bisa ditulis sebagai

log2 (512) = x

"Logaritma basis 2 dari 512 adalah x." Perhatikan “base 2”, mis. kami pikir dalam dua - berapa kali Anda perlu mengalikan 2 untuk mendapatkan 512.

Dalam algoritma pencarian biner, pada setiap langkah kami membagi array menjadi dua bagian.

Tambahan saya. Yaitu dalam kasus terburuk, kami melakukan operasi sebanyak yang kami bisa membagi array menjadi dua bagian. Misalnya, berapa kali kita dapat membagi array 4 elemen menjadi dua bagian? 2 kali. Dan array 8 elemen? 3 kali. Yaitu jumlah divisi / operasi = log2 (n) (di mana n adalah jumlah elemen dalam array).

Ternyata ketergantungan dari jumlah operasi pada jumlah elemen input digambarkan sebagai log2 (n)


Dengan demikian, menggunakan notasi Big O, algoritma pencarian biner memiliki kompleksitas O (log n).

Tingkatkan O (n ^ 2) menjadi O (n log n)

Mari kita kembali ke tugas memeriksa array untuk duplikat. Kami mengulangi semua elemen array, dan untuk setiap elemen kami mengulangi lagi. Mereka melakukan O (n) di dalam O (n), yaitu O (n * n) atau O (n ^ 2).

Kita dapat mengganti nested loop dengan pencarian biner *. Yaitu kita hanya harus melalui semua elemen O (n), di dalam kita lakukan O (log n). Ternyata O (n * log n), atau O (n log n).

 const nums = [1, 2, 3, 4, 5]; const searchFor = function (items, num) { //use binary search! //if found, return the number. Otherwise... //return null. We'll do this in a later chapter. } const hasDuplicates = function (nums) { for (let num of nums) { //let's go through the list again and have a look //at all the other numbers so we can compare if (searchFor(nums, num)) { return true; } } //only arrive here if there are no dups return false; } 

* PERHATIAN, untuk menghindari pencetakan . Menggunakan pencarian biner untuk memeriksa array untuk duplikat adalah solusi yang buruk. Ini hanya menunjukkan bagaimana, dalam istilah Big O, untuk mengevaluasi kompleksitas algoritma yang ditunjukkan dalam daftar kode di atas. Algoritma yang baik atau yang buruk tidak penting untuk artikel ini, visibilitas penting.

Berpikir dalam hal Big O

• Mendapatkan barang koleksi adalah O (1). Apakah itu diperoleh dengan indeks dalam array, atau dengan kunci dalam kamus dalam notasi O Besar, itu akan menjadi O (1)
• Iterasi atas koleksi adalah O (n)
• Loop bersarang atas koleksi yang sama adalah O (n ^ 2)
• Bagi dan Taklukkan selalu O (log n)
• Iterasi yang menggunakan Divide dan Conquer adalah O (n log n)