Saya ingat kesimpulan penting dari bagian sebelumnya. Untuk perilaku berurutan siklik yang tidak mengandung banyak sinyal (beralih satu siklus lebih dari dua kali), fungsi logis minimum dari setiap sinyal dapat direpresentasikan dalam bentuk berikut (secara alami, tanpa adanya konflik CSC):
1)
di mana a * b * ... * c adalah implan dari satu atau lebih variabel. g + h + ... + i - ini mungkin set kosong implan yang terdiri dari satu variabel. x * f adalah implan dari 2 variabel, keberadaan yang dalam bentuk minimal tidak diperlukan. Semua variabel, kecuali x, dapat dimasukkan dalam rumus baik dalam bentuk langsung dan terbalik, tergantung pada susunan tanda-tanda peristiwa yang sesuai. Semua variabel dimasukkan dalam rumus sebagai argumen hanya sekali.
Sebelum melanjutkan, kita akan melihat lebih dekat pada fenomena seperti dekomposisi. Pertama-tama, dekomposisi adalah hal yang menarik, yang menjaga sinkronisasi-diri. Saat mendekomposisi fungsi BUKAN-DAN-ATAU yang logis, seseorang dapat membedakan sebagai elemen baru:
a) satu atau lebih implan,
b) beberapa sinyal (variabel) dari satu implan,
c) satu input inverter.
Untuk mulai dengan, kami mempertimbangkan kasus khusus fungsi AND AND. Perilaku fungsi logis seperti itu (x = a + b + c + d) untuk model yang dimaksud:
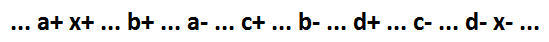
Dia dapat membedakan beberapa sinyal sebagai elemen terpisah.
Faktanya, pemilihan elemen baru selama dekomposisi adalah penambahan sinyal baru (f). Untuk menjaga perilaku yang benar, semi-modularitas, dan sinkronisasi-diri, pergantian sinyal yang baru ditambahkan f harus memiliki peristiwa konsekuensi. Karena dekomposisi hanya mempengaruhi satu elemen rangkaian (dalam hal ini, x) dan tidak mempengaruhi elemen-elemen yang tersisa dari rangkaian, mengalihkan sinyal f hanya dapat menyebabkan perpindahan sinyal x. Jika tidak, fungsi logis dari sinyal lain akan tergantung pada sinyal f. Dengan memberikan kesimpulan ini, mari kita coba menyoroti beberapa variabel kecuali variabel a sebagai elemen baru f. Ambil contoh variabel b dan c. Mereka membentuk elemen logis f = b + c.
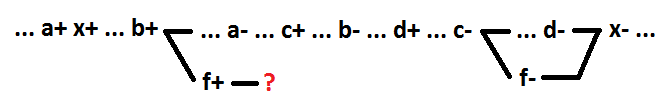
Seperti dapat dilihat, untuk peristiwa f + tidak mungkin untuk menentukan peristiwa konsekuensi tanpa melanggar kebenaran perilaku. Grup sinyal apa pun yang tidak mengandung variabel a tidak dapat dialokasikan sebagai elemen terpisah sambil tetap melakukan sinkronisasi diri.
Sinyal seperti dalam contoh ini akan dinamakan aktif. Dalam kasus umum, sinyal switching untuk fungsi OR (DAN) adalah sinyal, beralih ke 1 (0) mengubah nilai fungsi dari 0 ke 1 (dari 1 ke 0). Untuk mempertahankan sinkronisasi-diri selama dekomposisi fungsi logis ATAU (DAN) ketika memilih elemen baru, Anda harus menggunakan sinyal switching. Saat memilih elemen baru, perlu juga hanya menggunakan sinyal yang membentuk rantai yang terhubung (dalam contoh di bawah a + b). x = f + c + d, f = a + b.
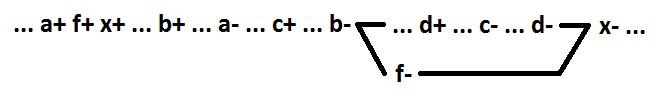
Saat menggunakan sinyal + b + d, sinkronisasi-sendiri tidak dipertahankan.
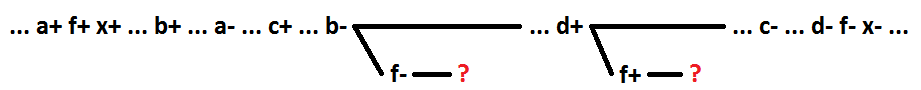
Dengan demikian, untuk perilaku berurutan tanpa beberapa sinyal selama dekomposisi fungsi logis OR (I), menyoroti sebagai elemen baru beberapa pertama dalam proses penyebaran sinyal, mulai dari yang termasuk, memastikan bahwa rangkaian disinkronkan sendiri.
Sekarang perhatikan fungsi non-OR (x =! A +! B). Sebagai elemen terpisah (f) sambil mempertahankan sinkronisasi-diri, kita hanya dapat memilih inverter input yang sesuai dengan sinyal switching (x = f +! B, f =! A). Pemisahan inverter input lain sebagai elemen yang terpisah akan menyebabkan pelanggaran sinkronisasi diri.
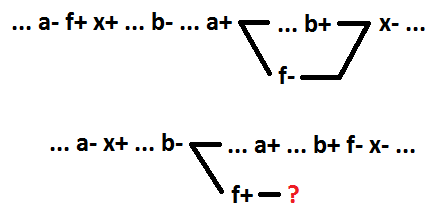
Mari beralih ke fungsi AND-OR. Demikian pula, sebagai sinyal switching untuk fungsi OR, kami mendefinisikan switching implant untuk fungsi AND-OR. Ini adalah implan, mengubah nilai yang dari 0 ke 1 mengarah ke perubahan nilai fungsi dari 0 menjadi 1. Demikian pula, seperti yang ditemukan untuk fungsi OR, untuk perilaku berurutan tanpa beberapa sinyal ketika menguraikan fungsi AND-OR logis, menyoroti beberapa yang pertama dalam proses penyebaran, yang tersirat, dimulai dengan penyertaan, menjamin pelestarian sinkronisasi-diri dari rangkaian. Kalau tidak, sinkronisasi diri akan terputus. Pada contoh di bawah ini, sebelum dekomposisi x = a * b + c. Setelah dekomposisi, x = f + c, f = a * b.
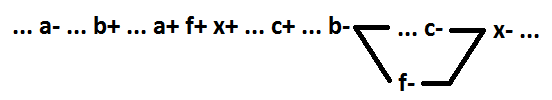
Sekarang untuk fungsi AND-OR, kami menganggap pemilihan sebagai elemen baru dari beberapa variabel yang termasuk dalam implan yang sama. Hanya fungsi minimal yang dipertimbangkan. Di bawah ini adalah semua opsi yang mungkin untuk contoh fungsi x = a * b * c + d (untuk opsi 4 - x = a * b * c + d + e, untuk opsi 6 - x = a * b * c * d + e) . Elemen yang disorot adalah f = a * b.

Dalam opsi 1, beralih salah satu sinyal yang dialokasikan (a +) adalah penyebab peristiwa x +. Dalam opsi 2, beralih salah satu sinyal yang dialokasikan (a-) adalah penyebab dari x-event. Dalam opsi 3 dan 4, pengalihan salah satu sinyal yang dialokasikan (masing-masing + dan a-) terletak di antara peristiwa x + dan x-, dan bukan merupakan penyebab peristiwa x-. Opsi 5 adalah kasus khusus dari opsi 4, ketika implan, di mana sinyal dialokasikan, inklusif. Pilihan yang tersisa 6 - semua pergantian sinyal yang dialokasikan terletak di antara peristiwa x- dan x +, dan bukan merupakan penyebab peristiwa x +.
Seperti yang Anda lihat, dalam opsi 1 dan 6, f-event tidak dapat diposisikan dengan benar. Transformasi semacam itu bukan dekomposisi dengan menjaga sinkronisasi-diri. Dalam opsi 2, 3 dan 4, sinkronisasi-diri dipertahankan. Tetapi nilai fungsi x ternyata berbeda dari f * c + d (f * c + d + e untuk 4 opsi). Untuk 2 opsi - x = f * (d + c), untuk 3 opsi x = c * x + d *! F + x *! F, untuk 4 opsi x = (f + d) * (e + c). Transformasi semacam itu bukanlah dekomposisi.
Hanya opsi 5 yang merupakan dekomposisi dengan mempertahankan sinkronisasi-diri (x = f * c + d). Dalam hal ini, sebagai elemen terpisah dalam implan inklusi, beberapa sinyal pertama dipilih, mulai dari inklusi (sinyal termasuk implan Dan sama dengan sinyal termasuk fungsi Dan). Tetapi, seperti yang ditunjukkan di atas, hasil serupa dicapai dalam dua langkah. Pertama, penyertaan implan disorot. Pada langkah kedua, beberapa sinyal pertama dipilih dalam elemen baru, dimulai dengan sinyal switching.
Mari kita beralih ke fungsi NON-DAN-OR. Mari kita memilih input inverter sebagai elemen terpisah. Sinyal a sesuai dengan input elemen x, yang terhubung dengan input inverter khusus (f =! A).
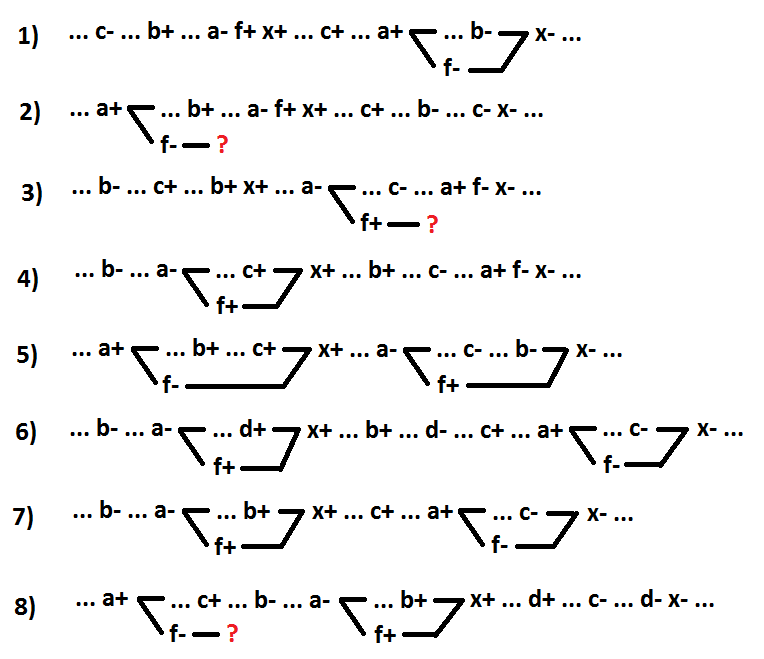
Opsi 1 dan 2 - sinyal switching a adalah penyebab peristiwa x + (1 - x =! A + b * c, 2 - x = b *! A + c). Opsi 3 dan 4 - mengganti sinyal a adalah penyebab kejadian x- (3 - x =! A + b * c, 4 - x =! A * b + c). Opsi 5 dan 6 - pengalihan sinyal a terletak antara peristiwa x + dan x-, dan bukan merupakan penyebab peristiwa x- (5 - x = b *! A + c, 6 - x =! A * b + d + c). Opsi 7 adalah kasus khusus dari opsi 6, ketika sinyal a adalah sinyal switching termasuk implan (x =! A * b + c). Pilihan yang tersisa 8 - semua pensaklaran sinyal a terletak di antara peristiwa x dan x +, dan bukan merupakan penyebab peristiwa x + (x = c *! A * b + d).
Seperti yang Anda lihat, opsi 2, 3 dan 8 bukanlah dekomposisi dengan menjaga sinkronisasi-diri, karena mustahil untuk memposisikan perpindahan sinyal dengan benar f. Untuk opsi 4, setelah konversi x = f * (c + b). Untuk opsi 5, setelah konversi x = c *! F +! F * x + b * x. Untuk opsi 6, setelah konversi x = (f + c) * (d + b). Transformasi ini (opsi 4, 5 dan 6) bukan dekomposisi. Untuk opsi 7, setelah konversi x = f * b + c. Opsi 7 adalah penguraian dengan pelestarian sinkronisasi diri. Dalam hal ini, inverter yang sesuai dengan sinyal switching termasuk implan dialokasikan sebagai elemen terpisah. Hasil serupa dicapai dalam dua langkah menggunakan transformasi di atas. Pertama, penyertaan implan disorot, kemudian inverter input dari sinyal sakelar dialokasikan untuk itu. Untuk opsi 1, setelah konversi x = f + b * c. Opsi 1 juga merupakan dekomposisi dengan menjaga sinkronisasi-diri. Ini adalah kasus khusus dari opsi 7, ketika penyertaan implan terdiri dari satu sinyal.
Kami mensistematisasikan hasil yang diperoleh. Untuk model yang dipertimbangkan, ketika menguraikan fungsi NOT-AND-OR yang logis untuk mempertahankan sinkronisasi-diri, hanya transformasi berikut yang dimungkinkan - alokasi sebagai elemen terpisah:
1 - satu atau lebih, mulai dari implan inklusif dan tumpang tindih (kasus khusus - untuk fungsi pemilihan NON-OR dari beberapa sinyal yang tumpang tindih, mulai dari inklusif);
2 - dalam inklusi implan beberapa, mulai dari inklusi, sinyal yang tumpang tindih;
3 - inverter input sesuai dengan sinyal switching termasuk implan (kasus khusus - untuk fungsi pemilihan NON-OR dari input input yang sesuai dengan sinyal switching).
Transformasi ini tidak memungkinkan implan menjadi inklusif jika tidak sebelum transformasi. Maka kesimpulannya: jika fungsi logis mengandung implan, yang terdiri dari lebih dari satu sinyal dan tidak inklusif, fungsi seperti itu tidak dapat difragmentasi menggunakan dekomposisi yang menjaga sinkronisasi diri, hingga dua elemen input. Setiap fungsi NOT-AND-OR logis di mana lebih dari satu variabel hanya berisi implan inklusif dapat dibagi menjadi dua elemen input (2AND-NOT, 2OR-NOT) menggunakan dekomposisi yang menjaga sinkronisasi diri.
Langkah 1 - jika elemen logis hanya berisi satu implant (atau semua implant terdiri dari satu variabel), lanjutkan ke langkah 3, jika tidak, lanjutkan ke langkah 2.
Langkah 2 - pilih sebagai elemen terpisah semua implan, kecuali satu, dimulai dengan inklusi. Selanjutnya, kami bekerja dengan item yang baru diterima. Lanjutkan ke langkah 1.
Langkah 3 - jika elemen terdiri dari dua variabel, lanjutkan ke langkah 5, jika tidak, lanjutkan ke langkah 4.
Langkah 4 - kami memilih sebagai elemen terpisah semua variabel, kecuali satu, dimulai dengan inklusi. Selanjutnya, kami bekerja dengan item yang baru diterima. Lanjutkan ke langkah 3.
Langkah 5 - berlaku untuk semua elemen input dua yang diterima.
Langkah 5.1 - jika inverter input berada di kedua input, kami akan mengonversi elemen menjadi ganda.
Langkah 5.2 - jika inverter input adalah satu dan sesuai dengan sinyal yang tidak aktif, kami akan mengonversi elemen menjadi yang ganda.
Langkah 5.3 - inverter input, jika ada, disorot sebagai elemen terpisah. Menghancurkan selesai.
Sekarang kembali ke rumus 1 di awal teks. Jika x * f yang tersirat tidak dalam ekspresi logis, maka fungsinya terlihat seperti ini: x = a * b * c + g + h + i. Perilakunya:
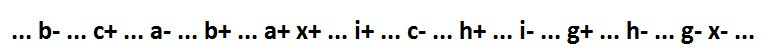
Seperti yang Anda lihat, satu-satunya implan dari lebih dari satu variabel (a * b * c) adalah inklusif. Dan fungsi ini dengan bantuan dekomposisi dapat difragmentasi menjadi komponen minimum sambil mempertahankan sinkronisasi diri.
Jika x * f implant hadir dalam ekspresi logis, maka fungsinya terlihat seperti ini: x = a * b * c + x * f + g + h + i. Perilakunya:
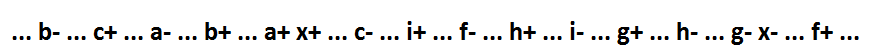
Implan x * f non-inklusif terdiri dari lebih dari satu variabel. Fungsi seperti itu tidak dapat difragmentasi sambil mempertahankan sinkronisasi diri. Tetapi kami menerapkan transformasi yang menjaga sinkronisasi-diri: tambahkan sinyal y - ganda ke sinyal x. Menambahkan sinyal y mengubah fungsi hanya sinyal x dan sinyal, pergantian yang merupakan konsekuensi dari peristiwa x- (variabel x digantikan oleh variabel y).
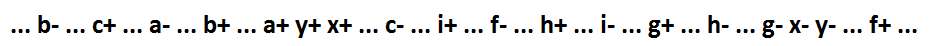
Sekarang x = (f + i + h + g) * y, y = c * b * a + x. Implan f + i + h + g dan c * b * a termasuk dan, masing-masing, fungsi x dan y dapat difragmentasi ke komponen minimum dengan tetap menjaga sinkronisasi diri.
Model perilaku yang disederhanakan (tanpa paralelisme, pilihan, dan banyak sinyal) memungkinkan Anda mengidentifikasi properti yang secara alami melekat dalam proses biner. Sintesis rangkaian sinkronisasi-diri secara minimal adalah fenomena alami yang tidak memerlukan desain apa pun.