Dalam artikel sebelumnya, saya menunjukkan betapa meluasnya masalah penyalahgunaan kriteria-t dalam publikasi ilmiah (dan ini hanya dapat dilakukan berkat keterbukaannya, dan sampah apa yang dibuat ketika digunakan dalam kursus, laporan, tugas pelatihan, dll. - tidak diketahui) . Untuk membahas ini, saya berbicara tentang dasar-dasar analisis varians dan tingkat signifikansi yang ditetapkan oleh peneliti sendiri. Tetapi untuk pemahaman penuh dari keseluruhan gambaran analisis statistik, perlu ditekankan sejumlah hal penting. Dan yang paling mendasar dari mereka adalah konsep kesalahan.
Aplikasi salah dan salah: apa bedanya?
Setiap sistem fisik mengandung beberapa jenis kesalahan, ketidaktepatan. Dalam bentuk yang paling beragam: toleransi yang disebut - perbedaan dalam ukuran produk yang berbeda dari jenis yang sama; karakteristik non-linear - ketika perangkat atau metode mengukur sesuatu sesuai dengan hukum terkenal dalam batas-batas tertentu, dan kemudian menjadi tidak berlaku; discreteness - ketika kita secara teknis tidak dapat memastikan karakteristik output yang lancar.
Dan pada saat yang sama, ada kesalahan manusia murni - penggunaan perangkat, instrumen, hukum matematika yang tidak benar. Ada perbedaan mendasar antara kesalahan yang melekat dalam sistem dan kesalahan dalam menerapkan sistem ini. Penting untuk membedakan dan tidak membingungkan di antara mereka sendiri dua konsep ini, yang disebut kata "kesalahan" yang sama. Dalam artikel ini, saya lebih suka menggunakan kata "kesalahan" untuk menunjukkan sifat-sifat sistem, dan "penggunaan yang salah" - untuk penggunaannya yang salah.
Artinya, kesalahan penguasa sama dengan toleransi peralatan, menempatkan goresan di kanvasnya. Kesalahan dalam arti penggunaan yang salah adalah menggunakannya saat mengukur detail jam tangan. Kesalahan steelyard tertulis di atasnya dan berjumlah sekitar 50 gram, dan penyalahgunaan steelyard adalah menimbang tas 25 kg di atasnya, yang membentang pegas dari wilayah hukum Hooke ke wilayah deformasi plastik. Kesalahan mikroskop kekuatan atom berasal dari kelonggarannya - Anda tidak bisa "menyentuh" objek dengan probe lebih kecil dari diameter atom. Tetapi ada banyak cara untuk menyalahgunakannya atau salah mengartikan data. Dan sebagainya.
Jadi, kesalahan macam apa yang ada dalam metode statistik ini? Dan kesalahan ini justru tingkat signifikansi yang terkenal α.
Kesalahan jenis pertama dan kedua
Kesalahan dalam alat matematika statistik adalah esensi probabilistik Bayesian itu sendiri. Dalam artikel terakhir, saya telah menyebutkan metode statistik apa yang didasarkan pada: menentukan tingkat signifikansi α sebagai probabilitas terbesar yang dapat diterima untuk secara ilegal menolak hipotesis nol, dan peneliti untuk secara independen memberikan nilai ini kepada peneliti.
Apakah Anda sudah melihat konvensi ini? Bahkan, dalam metode kriteria tidak ada kekakuan matematika yang akrab. Matematika beroperasi pada karakteristik probabilistik.
Dan inilah titik lain di mana salah tafsir atas satu kata dalam konteks yang berbeda dimungkinkan. Penting untuk membedakan antara konsep probabilitas dan implementasi aktual suatu peristiwa, yang dinyatakan dalam distribusi probabilitas. Misalnya, sebelum memulai eksperimen apa pun, kami tidak tahu nilai seperti apa yang akan kami dapatkan sebagai hasilnya. Ada dua kemungkinan hasil: setelah membuat nilai hasil tertentu, kita akan benar-benar mendapatkannya atau tidak. Adalah logis bahwa probabilitas kedua peristiwa adalah 1/2. Tetapi kurva Gaussian yang ditunjukkan pada artikel sebelumnya menunjukkan
distribusi probabilitas bahwa kita menebak dengan tepat kebetulan.
Anda dapat dengan jelas menggambarkan ini dengan sebuah contoh. Mari kita putar dua dadu 600 kali - teratur dan curang. Kami mendapatkan hasil sebagai berikut:

Sebelum percobaan, untuk kedua kubus hilangnya wajah apa pun akan sama-sama memungkinkan - 1/6. Namun, setelah percobaan, esensi dari kubus kecurangan muncul, dan kita dapat mengatakan bahwa kepadatan probabilitas keenam jatuh di dalamnya adalah 90%.
Contoh lain yang diketahui oleh ahli kimia, ahli fisika, dan siapa pun yang tertarik dengan efek kuantum adalah orbital atom. Secara teoritis, sebuah elektron dapat "dioleskan" di ruang angkasa dan terletak hampir di mana saja. Tetapi dalam praktiknya ada bidang-bidang di mana 90 persen atau lebih kasus. Daerah-daerah ruang ini dibentuk oleh permukaan dengan kerapatan probabilitas elektron yang ada 90% adalah orbital atom klasik dalam bentuk bola, halter, dll.
Jadi, dengan menetapkan level signifikansi secara independen, kami dengan sengaja menyetujui kesalahan yang dijelaskan dalam namanya. Karena itu, tidak ada satu pun hasil yang dapat dianggap "sepenuhnya dapat diandalkan" - selalu kesimpulan statistik kami akan mengandung beberapa kemungkinan kegagalan.
Kesalahan yang dirumuskan dengan menentukan tingkat signifikansi α disebut
kesalahan jenis pertama . Ini dapat didefinisikan sebagai "alarm salah", atau, lebih tepatnya, hasil positif palsu. Sebenarnya, apa arti kata “menolak hipotesis nol” dengan salah? Ini berarti secara keliru mengambil data yang diamati untuk perbedaan yang signifikan antara kedua kelompok. Untuk membuat diagnosa yang salah tentang keberadaan penyakit, terburu-buru untuk mengungkapkan kepada dunia penemuan baru, yang sebenarnya tidak ada - ini adalah contoh kesalahan dari jenis pertama.
Tetapi, haruskah ada hasil negatif palsu? Benar sekali, dan mereka disebut
kesalahan jenis kedua . Contohnya adalah diagnosis atau kekecewaan sebelum waktunya sebagai hasil dari penelitian, meskipun sebenarnya itu berisi data penting. Kesalahan jenis kedua ditunjukkan oleh huruf, anehnya, β. Tetapi konsep ini sendiri tidak begitu penting untuk statistik seperti angka 1-β. Angka 1-β disebut
kekuatan kriteria , dan seperti yang Anda tebak, itu mencirikan kemampuan kriteria untuk tidak melewatkan peristiwa penting.
Namun, konten dalam metode statistik kesalahan jenis pertama dan kedua tidak hanya keterbatasan mereka. Konsep kesalahan ini dapat digunakan secara langsung dalam analisis statistik. Bagaimana?
Analisis ROC
Analisis ROC (dari karakteristik operasi penerima) adalah metode untuk mengukur penerapan atribut tertentu ke klasifikasi objek biner. Sederhananya, kita dapat menemukan beberapa cara untuk membedakan orang sakit dari orang sehat, kucing dari anjing, hitam dari putih, dan kemudian memeriksa validitas metode ini. Mari kita lihat contoh lagi.
Biarkan Anda menjadi ilmuwan forensik pemula, dan kembangkan cara baru untuk secara diam-diam dan tegas menentukan apakah seseorang adalah penjahat. Anda datang dengan tanda kuantitatif: untuk mengevaluasi kecenderungan kriminal orang dengan frekuensi mereka mendengarkan Mikhail Krug. Tetapi apakah gejala Anda akan memberikan hasil yang memadai? Mari kita perbaiki.
Anda akan membutuhkan dua kelompok orang untuk memvalidasi kriteria Anda: warga negara biasa dan penjahat. Memang, mari kita asumsikan bahwa rata-rata waktu tahunan mereka mendengarkan Mikhail Krug berbeda (lihat gambar):
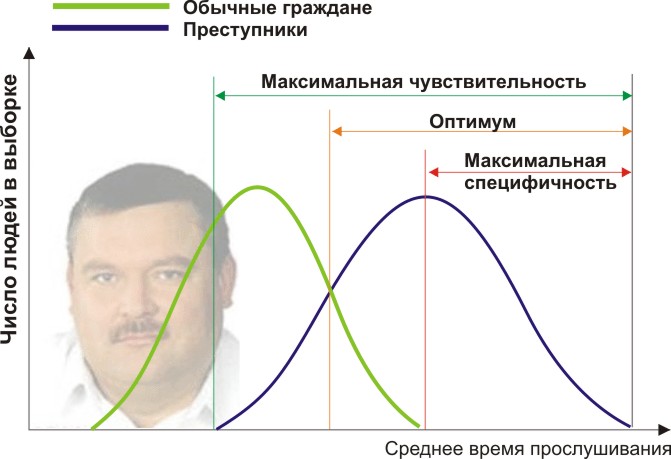
Di sini kita melihat bahwa dengan tanda kuantitatif waktu mendengarkan, sampel kami berpotongan. Seseorang mendengarkan Circle secara spontan di radio tanpa melakukan kejahatan, dan seseorang melanggar hukum dengan mendengarkan musik lain atau bahkan tuli. Kondisi batas apa yang kita miliki? Analisis ROC memperkenalkan konsep selektivitas (sensitivitas) dan spesifisitas. Sensitivitas didefinisikan sebagai kemampuan untuk mengidentifikasi semua poin yang menarik bagi kami (dalam contoh ini, penjahat), dan kekhususan - tidak untuk menangkap sesuatu yang positif palsu (tidak untuk membuat penduduk biasa dicurigai). Kita dapat mengatur beberapa sifat kuantitatif kritis yang memisahkan beberapa dari yang lain (oranye), mulai dari sensitivitas maksimum (hijau) hingga spesifisitas maksimum (merah).
Mari kita lihat diagram berikut:

Dengan menggeser nilai atribut kami, kami mengubah rasio hasil false-positif dan false-negatif (area di bawah kurva). Dengan cara yang sama, kita dapat mendefinisikan Sensitivitas = Posisi. Res-t / (Res-Positif + t-false-negatif. Res-t) dan Spesifisitas = Neg. Res-t / (Negatif Res-t + false-positive. Res-t).
Tetapi yang paling penting, kita dapat mengevaluasi rasio hasil positif ke hasil positif palsu pada seluruh rentang nilai atribut kuantitatif kita, yang merupakan kurva ROC yang kita inginkan (lihat gambar):

Dan bagaimana kita memahami dari grafik ini seberapa baik atribut kita? Sangat sederhana, hitung area di bawah kurva (AUC, area di bawah kurva). Garis putus-putus (0,0; 1,1) berarti kebetulan lengkap dari dua sampel dan kriteria yang sama sekali tidak berarti (area di bawah kurva adalah 0,5 dari seluruh kuadrat). Tetapi cembungnya kurva ROC hanya menunjukkan kesempurnaan kriteria. Jika kami berhasil menemukan kriteria sedemikian rupa sehingga sampel tidak akan berpotongan sama sekali, maka area di bawah kurva akan menempati seluruh grafik. Secara umum, sifat tersebut dianggap baik, memungkinkan seseorang untuk memisahkan satu sampel dengan andal jika AUC> 0,75-0,8.
Dengan analisis ini, Anda dapat memecahkan berbagai masalah. Setelah memutuskan bahwa terlalu banyak ibu rumah tangga dicurigai karena Michael Krug, dan di samping itu, pelanggar berulang berbahaya yang mendengarkan Noggano terlewatkan, Anda dapat menolak kriteria ini dan mengembangkan yang lain.
Setelah muncul sebagai cara pemrosesan sinyal radio dan mengidentifikasi "teman atau musuh" setelah serangan di Pearl Harbor (maka nama aneh untuk karakteristik penerima), analisis ROC telah menemukan aplikasi luas dalam statistik biomedis untuk analisis, validasi, pembuatan, dan karakterisasi panel biomarker dll. Ini fleksibel untuk digunakan jika didasarkan pada logika suara. Misalnya, Anda dapat mengembangkan indikasi untuk pemeriksaan medis pasien inti yang sudah pensiun dengan menerapkan kriteria yang sangat spesifik, meningkatkan efisiensi mendeteksi penyakit jantung dan tidak membebani dokter dengan pasien yang tidak perlu. Dan selama epidemi berbahaya dari virus yang sebelumnya tidak diketahui, sebaliknya, Anda dapat menemukan kriteria yang sangat selektif sehingga tidak ada orang lain yang benar-benar lolos dari vaksinasi.
Kami bertemu dengan kesalahan dari kedua jenis dan visibilitas mereka dalam deskripsi kriteria yang divalidasi. Sekarang, bergerak dari fondasi logis ini, kita dapat menghancurkan serangkaian deskripsi stereotip yang salah tentang hasilnya. Beberapa formulasi yang salah menangkap pikiran kita, sering bingung dengan kata-kata dan konsep yang sama, dan juga karena sangat sedikit perhatian yang diberikan pada interpretasi yang salah. Ini, mungkin, perlu ditulis secara terpisah.