Algoritma triangulasi delaunay dengan metode garis menyapu

Hari baik!

Pada artikel ini, saya akan menjelaskan secara terperinci algoritma yang saya peroleh sebagai hasil dari menggunakan gagasan "menyapu garis lurus" untuk membangun triangulasi Delaunay di pesawat. Ada beberapa ide di dalamnya yang tidak pernah saya temui ketika saya membaca artikel tentang triangulasi.
Mungkin seseorang juga akan menemukan mereka tidak biasa. Saya akan mencoba melakukan segalanya dalam tradisi terbaik dan memasukkan hal-hal berikut dalam cerita: deskripsi struktur data yang digunakan, deskripsi langkah-langkah algoritma, bukti kebenaran, perkiraan waktu, serta perbandingan dengan algoritma berulang menggunakan pohon kD.

Definisi dan pernyataan masalah

Triangulasi

Mereka mengatakan bahwa triangulasi ditentukan pada himpunan titik-titik di pesawat jika beberapa pasang titik dihubungkan oleh suatu tepi, setiap permukaan yang terbatas pada grafik yang dihasilkan membentuk segitiga, ujung-ujungnya tidak berpotongan, dan grafik maksimal dalam jumlah tepi.

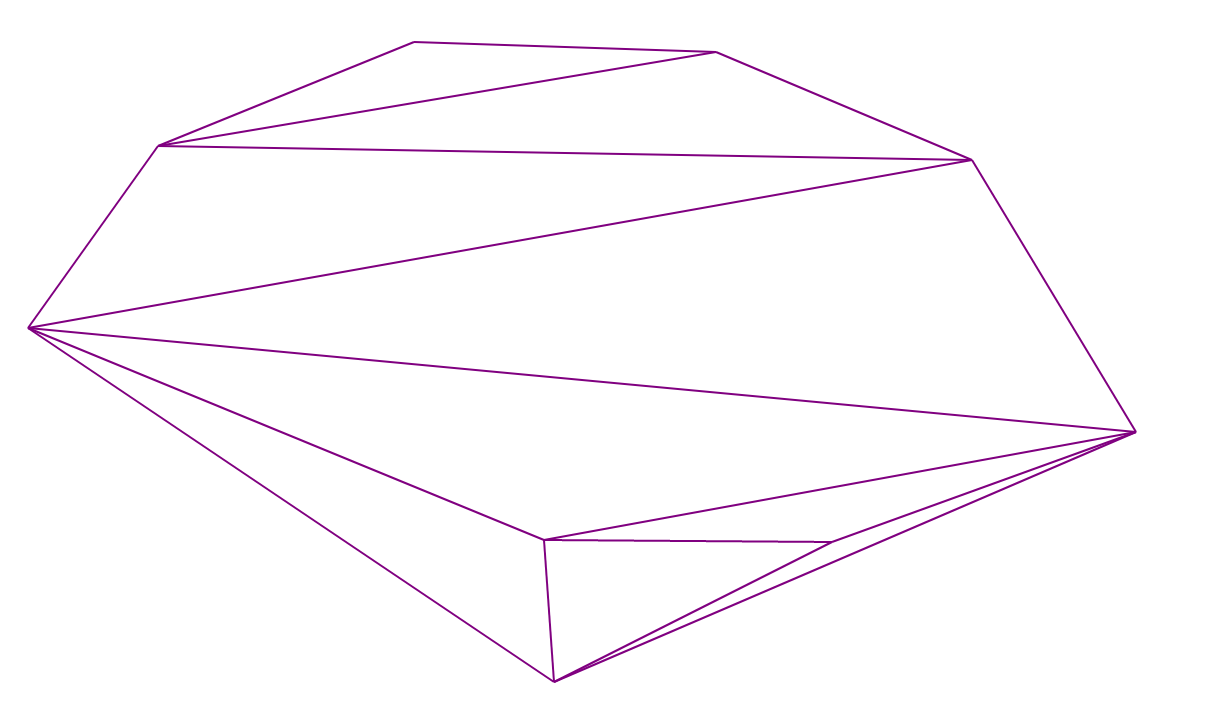
Triangulasi Delaunay

Triangulasi Delaunay adalah triangulasi di mana untuk segitiga apa pun memang benar bahwa tidak ada titik dari set asli di dalam lingkaran yang dibatasi di sekitarnya.

Catatan : untuk sekumpulan poin tertentu di mana tidak ada 4 poin pada lingkaran yang sama, tepat ada satu triangulasi Delaunay.

Kondisi Delaunay

Biarkan triangulasi diberikan pada set poin. Kami mengatakan bahwa subset poin tertentu memenuhi kondisi Delaunay jika triangulasi yang terikat pada subset ini adalah triangulasi Delaunay untuknya.

Kriteria untuk Triangulasi Delaunay

Pemenuhan kondisi Delaunay untuk semua poin yang membentuk segi empat dalam triangulasi sama dengan fakta bahwa triangulasi ini adalah triangulasi Delaunay.

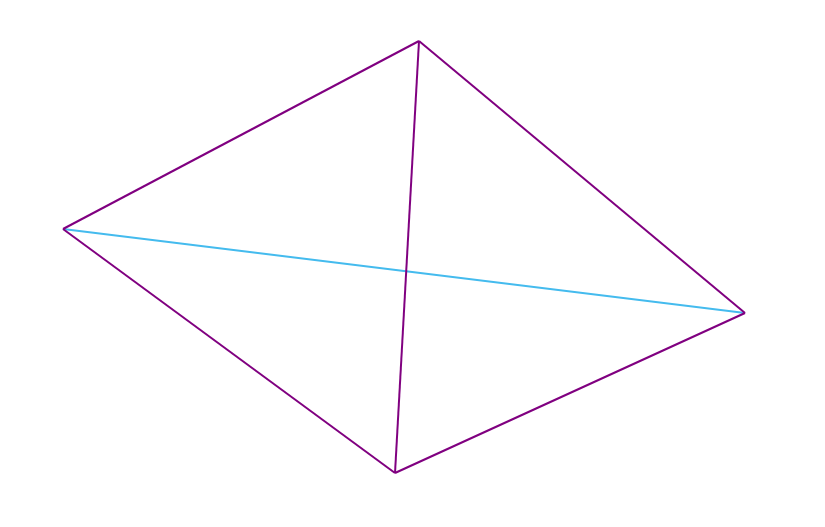
Catatan : untuk quadrangles non-cembung, kondisi Delaunay selalu terpenuhi, dan untuk quadrangles cembung (yang simpulnya tidak terletak pada lingkaran yang sama) ada 2 kemungkinan triangulasi (salah satunya adalah triangulasi Delaunay).

Tugasnya adalah membangun triangulasi Delaunay untuk sekumpulan poin tertentu.

Deskripsi algoritma

Titik yang terlihat dan tepi yang terlihat

Biarkan lambung cembung minimal (selanjutnya, MBO) diberikan dari himpunan titik yang terbatas (ujung-ujungnya menghubungkan beberapa titik sehingga mereka membentuk poligon yang mengandung semua titik himpunan) dan titik A yang terletak di luar lambung. Maka titik pesawat disebut terlihat untuk titik A, jika segmen yang menghubungkannya ke titik A tidak memotong MBO.

Tepi MBO disebut terlihat untuk titik A jika ujungnya terlihat untuk A.

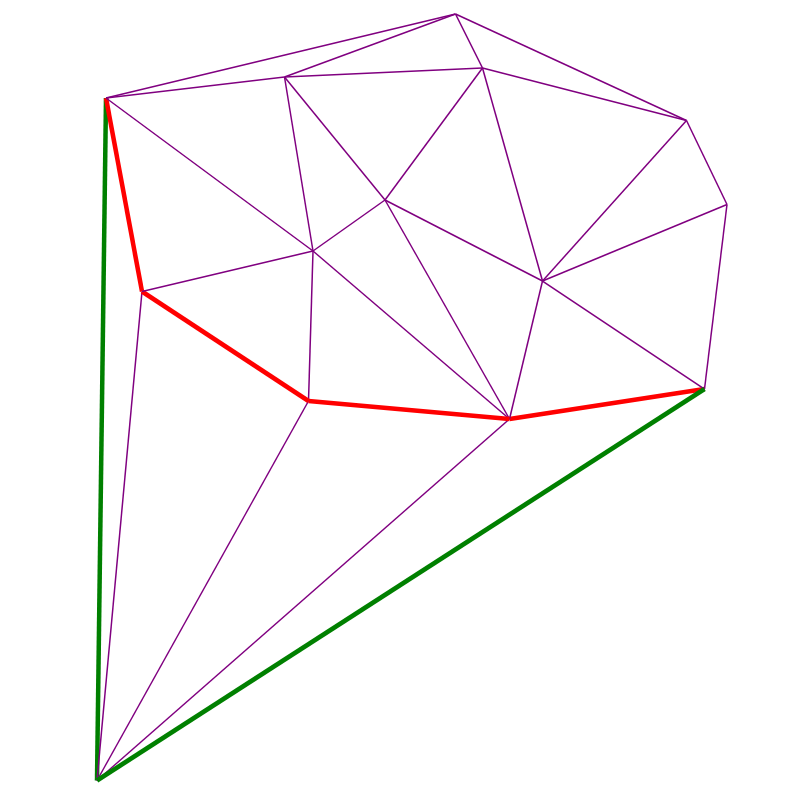
Pada gambar berikut, tepi yang terlihat untuk titik merah ditandai dengan warna merah:

Catatan : kontur triangulasi Delaunay adalah MBO untuk titik-titik di mana ia dibangun.

Catatan 2 : dalam algoritma, tepi terlihat untuk titik yang ditambahkan A membentuk rantai, yaitu, beberapa tepi MBO berturut-turut

Menyimpan triangulasi dalam memori

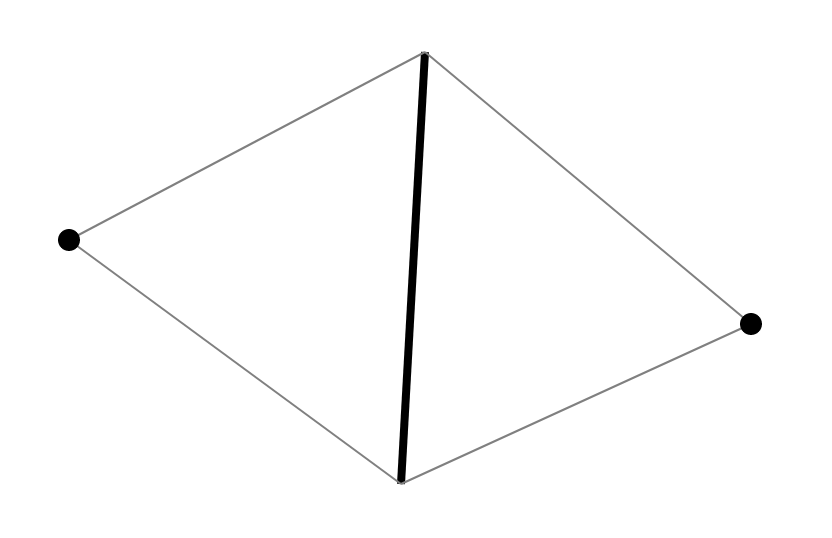
Ada beberapa metode standar yang dijelaskan dengan baik dalam buku Skvortsov [1]. Karena spesifik dari algoritma, saya akan menawarkan versi saya sendiri. Karena kami ingin memeriksa 4-gons untuk kondisi Delaunay, kami mempertimbangkan strukturnya. Setiap segi empat dalam triangulasi adalah 2 segitiga yang memiliki tepi yang sama. Setiap tepian memiliki tepat 2 segitiga yang berdekatan dengannya. Dengan demikian, setiap segi empat dalam triangulasi dihasilkan oleh satu tepi dan dua simpul berlawanan dengan tepi dalam segitiga yang berdekatan.
Karena dua segitiga dan kedekatannya dipulihkan di sepanjang tepi dan dua simpul, kita dapat mengembalikan triangulasi untuk semua struktur tersebut. Oleh karena itu, diusulkan untuk menyimpan tepi dengan dua simpul di set dan melakukan pencarian di sepanjang tepi (sepasang simpul yang dipesan).

Algoritma

Gagasan garis sapuan adalah bahwa semua titik diurutkan dalam satu arah, dan kemudian diproses secara bergantian.

1. Urutkan semua titik di sepanjang garis lurus (untuk kesederhanaan, dengan koordinat $$$x$)
2. Kami membangun segitiga pada 3 poin pertama.
   
   Selanjutnya, untuk setiap poin berikutnya kami akan melakukan langkah-langkah yang menjaga invarian bahwa ada triangulasi Delaunay untuk poin yang sudah ditambahkan dan, karenanya, MBO untuk mereka.
3. Tambahkan segitiga yang dibentuk oleh tepi yang terlihat dan titik itu sendiri (yaitu, tambahkan tepi dari titik yang dimaksud ke semua ujung tepi yang terlihat).
4. Kami memeriksa kondisi Delaunay semua segi empat yang dihasilkan oleh tepi yang terlihat. Jika kondisinya tidak terpenuhi di suatu tempat, maka kami membangun kembali triangulasi dalam segi empat (saya ingat bahwa hanya ada dua dari mereka) dan secara rekursif menjalankan pemeriksaan untuk segi empat yang dihasilkan oleh tepi segi empat saat ini (karena hanya setelah mereka kondisi Delaunay dapat dilanggar).

Catatan : pada langkah (4) selama permulaan rekursif, Anda tidak dapat memeriksa kuadrangel yang dihasilkan oleh tepi yang berasal dari titik yang dipertimbangkan pada iterasi ini (selalu ada dua dari empat di antaranya). Paling sering mereka tidak cembung, karena cembung buktinya murni geometris, saya akan menyerahkannya kepada pembaca. Selanjutnya, kami mengasumsikan bahwa hanya 2 awal rekursif yang dilakukan untuk setiap pembangunan kembali.

Memverifikasi Kondisi Delaunay

Cara untuk menguji segi empat untuk kondisi Delaunay dapat ditemukan dalam buku yang sama [1]. Saya hanya mencatat bahwa ketika memilih metode dengan fungsi trigonometri dari sana, dengan implementasi yang tidak akurat, nilai negatif dari sinus dapat diperoleh, masuk akal untuk mengambilnya modulo.

Cari tepi yang terlihat

Masih memahami bagaimana menemukan tepi yang terlihat secara efektif. Perhatikan bahwa titik tambah sebelumnya S adalah dalam MBO pada iterasi saat ini, karena memiliki koordinat terbesar $$$x$, dan juga terlihat untuk titik saat ini. Kemudian, dengan memperhatikan bahwa ujung-ujung tepi yang terlihat membentuk rantai kontinyu dari titik-titik yang terlihat, kita dapat pergi dari titik S di kedua arah sepanjang MBO dan mengumpulkan ujung-ujungnya selagi terlihat (visibilitas tepi diperiksa menggunakan produk vektor). Dengan demikian, mudah untuk menyimpan MBO sebagai daftar yang terhubung dua kali lipat, pada setiap iterasi menghapus tepi yang terlihat dan menambahkan 2 yang baru dari titik yang dipertimbangkan.

Visualisasi algoritma

Dua titik merah - ditambahkan dan sebelumnya. Tepi merah pada setiap saat membentuk tumpukan rekursi dari langkah (4):

Algoritma benar

Untuk membuktikan kebenaran algoritma, cukup membuktikan konservasi invarian dalam langkah (3) dan (4).

Langkah (3)

Setelah langkah (3), jelas, kita mendapatkan triangulasi dari set poin saat ini.

Langkah (4)

Dalam proses langkah (4), semua segi empat yang tidak memenuhi kondisi Delaunay berada di tumpukan rekursi (mengikuti dari deskripsi), yang berarti bahwa pada akhir langkah (4) semua segi empat memenuhi kondisi Delaunay, yaitu, triangulasi Delaunay sebenarnya dibangun. Maka tetap membuktikan bahwa proses pada langkah (4) suatu hari nanti akan berakhir. Ini mengikuti dari fakta bahwa semua tepi yang ditambahkan selama pembangunan kembali berasal dari simpul saat ini yang dipertanyakan (mis., Dalam langkah $$$k$tidak ada lagi $$$k-1$) dan dari fakta bahwa setelah menambahkan tepi ini kami tidak akan mempertimbangkan segi empat yang dihasilkan oleh mereka (lihat komentar sebelumnya), yang berarti kami tidak akan menambahkan lebih dari sekali.

Kompleksitas waktu

Rata-rata, algoritma bekerja dengan sangat baik pada distribusi normal yang seragam (hasilnya ditunjukkan pada tabel di bawah). Ada asumsi bahwa waktu kerjanya adalah $$$O (NlogN)$. Dalam kasus terburuk, penilaian dilakukan $$$O (N ^ 2)$.

Mari kita lihat waktu kerja di beberapa bagian dan memahami mana yang memiliki dampak terbesar pada total waktu:

Sortir menurut arah

Untuk menyortir, kami akan menggunakan estimasi $$$O (NlogN)$.

Cari tepi yang terlihat

Pertama, kami menunjukkan bahwa total waktu yang dihabiskan untuk mencari tepi yang terlihat adalah $$$O (N)$. Perhatikan bahwa pada setiap iterasi kami menemukan semua tepi yang terlihat dan 2 lebih (pertama tidak terlihat) dalam waktu linier. Pada langkah (3), kami menambahkan 2 tepi baru ke MBO. Jadi, secara total, tidak lebih dari $$$2N$tulang rusuk, oleh karena itu, dan berbagai tulang rusuk yang terlihat tidak akan lagi $$$2N$. Kami juga akan menemukan $$$2N$tepi yang tidak terlihat. Dengan demikian, secara total tidak ada lagi $$$4N$tulang rusuk yang sesuai dengan waktu $$$O (N)$.

Membangun segitiga baru

Total waktu untuk membangun segitiga dari langkah (3) dengan tepi yang terlihat sudah ditemukan jelas $$$O (N)$.

Membangun kembali triangulasi

Masih berurusan dengan langkah (4). Pertama, perhatikan bahwa memeriksa kondisi Delaunay dan membangun kembali jika tidak terpenuhi adalah tindakan yang cukup mahal (meskipun mereka berhasil $$$O (1)$) Hanya dengan memeriksa kondisi Delaunay dapat mengambil sekitar 28 operasi aritmatika. Mari kita lihat jumlah rata-rata pembangunan kembali selama langkah ini. Hasil praktis pada beberapa distribusi diberikan di bawah ini. Bagi mereka saya benar-benar ingin mengatakan bahwa jumlah rata-rata penataan ulang tumbuh dengan kecepatan logaritmik, tetapi mari kita tinggalkan ini sebagai asumsi.

Di sini saya juga ingin mencatat bahwa jumlah rata-rata pengaturan ulang per titik dapat sangat bervariasi dari arah sepanjang penyortiran dilakukan. Jadi, untuk satu juta yang terdistribusi secara merata pada persegi panjang rendah dengan rasio aspek 100000: 1, angka ini bervariasi dari 1,2 hingga 24 (nilai-nilai ini dicapai ketika menyortir data secara horizontal dan vertikal, masing-masing). Oleh karena itu, saya melihat titik dalam memilih arah pengurutan secara sewenang-wenang (dalam contoh ini, dengan pemilihan sewenang-wenang, rata-rata sekitar 2 pembangunan kembali diperoleh) atau secara manual memilihnya jika data diketahui sebelumnya.

Jadi, waktu utama program biasanya diperlukan untuk langkah (4). Jika berjalan cepat, masuk akal untuk berpikir tentang mempercepat penyortiran.

Kasus terburuk

Kasus terburuk aktif $$$k$iterasi terjadi $$$k-1$panggilan rekursif pada langkah (4), yaitu, menjumlahkan semua i, kita mendapatkan perilaku asimptotik dalam kasus terburuk $$$O (N ^ 2)$. Gambar berikut menggambarkan contoh yang indah di mana program dapat bekerja untuk waktu yang lama (rata-rata 1.100 dibangun kembali ketika menambahkan titik baru dengan input 10.000 poin).

Perbandingan dengan algoritma iteratif untuk membangun triangulasi Delaunay menggunakan kD-tree

Deskripsi algoritma berulang

Saya akan menjelaskan secara singkat algoritma di atas. Ketika titik berikutnya tiba, kita menggunakan kD-tree (saya sarankan Anda untuk membacanya di suatu tempat, jika Anda tidak tahu), kami menemukan sebuah segitiga yang sudah cukup dekat dengannya. Kemudian melewati kedalaman kita mencari segitiga, di mana titik itu sendiri jatuh. Kami memperluas tepi ke simpul dari segitiga yang ditemukan dan benar-benar melakukan langkah (4) dari algoritma kami untuk segi empat baru. Karena titik dapat berada di luar triangulasi, untuk penyederhanaan diusulkan untuk mencakup semua titik dengan segitiga besar (untuk membangunnya di muka), ini akan menyelesaikan masalah.

Kesamaan algoritma

Bahkan, jika poin ditambahkan dalam urutan diurutkan berdasarkan arah, maka algoritma kami benar-benar berfungsi sama seperti berulang, kecuali bahwa jumlah penataan ulang kurang. Animasi berikut menunjukkan ini dengan sempurna. Di atasnya, titik ditambahkan dari kanan ke kiri, dan mereka semua ditutupi oleh segitiga besar, yang kemudian dihapus.

Perbedaan Algoritma

Dalam algoritma iteratif, lokalisasi titik (mencari segitiga yang diinginkan) terjadi rata-rata lebih $$$O (logN)$, pada distribusi di atas, rata-rata, 3 pengaturan ulang terjadi (seperti yang ditunjukkan pada [1]) di bawah kondisi urutan pasokan poin yang sewenang-wenang. Dengan demikian, garis sweeping memenangkan waktu dari algoritma iteratif dalam pelokalan, tetapi kehilangan dalam membangun kembali (yang, saya ingat, cukup sulit). Selain itu, algoritma berulang bekerja online, yang juga merupakan fitur pembeda.

Kesimpulan

Di sini saya hanya menunjukkan beberapa triangulasi menarik yang dihasilkan dari pengoperasian algoritma.

Pola yang indah

Distribusi normal, 1000 poin

Pemerataan, 1000 poin

Triangulasi dibangun di lokasi semua kota di Rusia

Di sini Anda dapat melihat contoh kode saya untuk algoritma ini:
github.com/Vemmy124/Delaunay-Triangulation-Algorithm

Terima kasih atas perhatian anda!

Sastra

[1] Skvortsov A.V. Delaunay triangulasi dan penerapannya. - Tomsk: Rumah penerbitan Tom. University, 2002 .-- 128 hal. ISBN 5-7511-1501-5