Posting klasik ini merinci cara paling populer untuk membuat dan melewati labirin. Artikel ini dibagi menjadi empat bagian: klasifikasi, algoritma pembangkitan, algoritma untuk memecahkan labirin dan operasi lainnya dengan labirin.Klasifikasi labirin
Labirin secara keseluruhan (dan karenanya algoritma untuk membuatnya) dapat dibagi menjadi tujuh klasifikasi yang berbeda: dimensi, hyperdimension, topologi, tessellation, routing, tekstur dan prioritas. Labirin dapat menggunakan satu elemen dari setiap kelas dalam kombinasi apa pun.
Dimensi: kelas dimensi pada dasarnya menentukan berapa banyak dimensi di ruang yang diisi labirin. Jenis-jenis berikut tersedia:

Dua dimensi : sebagian besar labirin, baik kertas dan nyata, memiliki dimensi ini, yaitu, kita selalu dapat menampilkan rencana labirin pada selembar kertas dan bergerak di sepanjang itu tanpa melintasi koridor lain dari labirin.- Tiga dimensi : labirin tiga dimensi memiliki beberapa tingkatan; di dalamnya (setidaknya dalam versi ortogonal), bagian-bagian dapat, di samping empat arah mata angin, turun dan naik. Labirin 3D sering divisualisasikan sebagai array level 2D dengan naik turun tangga.
Dimensi yang lebih tinggi : Anda dapat membuat labirin empat dimensi dan bahkan lebih multidimensi. Kadang-kadang mereka divisualisasikan sebagai labirin 3D dengan "portal" memimpin melalui dimensi keempat, misalnya, portal ke "masa lalu" dan "masa depan".
Menjalin : labirin dengan menjalin - ini pada dasarnya adalah labirin dua dimensi (atau lebih tepatnya 2,5 dimensi), di mana, bagaimanapun, bagian dapat tumpang tindih satu sama lain. Saat ditampilkan, biasanya cukup jelas di mana buntu dan bagaimana satu bagian di atas yang lain. Labirin dari dunia nyata, di mana ada jembatan yang menghubungkan satu bagian labirin dengan yang lain, sebagian terjalin.
Hyperdimension: klasifikasi menurut hyperdimension sesuai dengan dimensi objek yang bergerak melalui labirin, dan bukan labirin itu sendiri. Jenis-jenis berikut tersedia:

Non-hyperlabyrinths : hampir semua labirin, bahkan yang dibuat dalam dimensi tinggi atau dengan aturan khusus, biasanya non-hyperlabyrinths. Di dalamnya kita bekerja dengan titik atau objek kecil, misalnya, bola atau pemain sendiri, yang bergerak dari titik ke titik, dan rute beraspal membentuk garis. Di setiap titik, ada jumlah pilihan yang mudah dihitung.- Hyperlabyrinths: hyperlabyrinths adalah labirin di mana objek yang dipecahkan bukan hanya sebuah titik. Hyperlabyrinth standar (atau hyperlabyrinth orde pertama) terdiri dari garis yang membentuk permukaan saat bergerak di sepanjang jalan. Hyperlabyrinth hanya bisa ada dalam 3D atau dalam medium dengan dimensi yang lebih besar, dan pintu masuk ke hyperlabyrinth seringkali bukan sebuah titik, melainkan sebuah garis. Hyperlabyrinth secara fundamental berbeda, karena itu perlu untuk memperhitungkan dan secara bersamaan bekerja dengan beberapa bagian di sepanjang garis, dan pada waktu tertentu ada jumlah negara yang hampir tak terbatas dan opsi untuk apa yang dapat dilakukan dengan garis. Garis solusi tidak terbatas, atau titik akhir berada di luar hyperlabyrinth untuk menghindari garis yang dikompresi ke titik, karena dalam kasus ini dapat dianggap sebagai non-hyperlabyrinth.
- Hyper-hyperlabyrinth: hyperlabyrinths dapat memiliki dimensi tinggi yang berubah-ubah. Hyper-hyperlabyrinth (atau hyperlabyrinth orde kedua) kembali meningkatkan dimensi objek yang sedang diselesaikan. Di sini, objek yang akan dipecahkan adalah pesawat, yang, ketika bergerak di sepanjang jalan, membentuk sosok tiga dimensi. Hyper-hyperlabyrinth hanya bisa ada di lingkungan 4D atau dimensi yang lebih tinggi.
Topologi: Kelas topologi menggambarkan geometri ruang labirin tempat keberadaannya secara keseluruhan. Jenis-jenis berikut tersedia:

Normal : Ini adalah labirin standar di ruang Euclidean.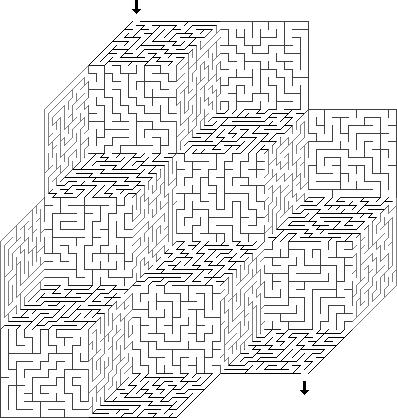
Planair : Istilah "planair" menggambarkan setiap labirin dengan topologi yang tidak biasa. Biasanya ini berarti bahwa ujung-ujung labirin terhubung dengan cara yang menarik. Contoh: labirin di permukaan kubus, labirin di permukaan jalur Mobius dan labirin setara dengan yang ada di torus di mana sisi kiri dan kanan, atas dan bawah terhubung berpasangan.
Tessellation: klasifikasi geometri sel-sel individu yang membentuk labirin. Jenis yang ada:

Orthogonal : Ini adalah kotak persegi panjang standar di mana sel memiliki bagian berpotongan pada sudut kanan. Dalam konteks tessellation, mereka juga bisa disebut labirin gamma.
Delta : Delta labirin terdiri dari segitiga yang terhubung, dan setiap sel dapat memiliki hingga tiga bagian yang terhubung dengannya.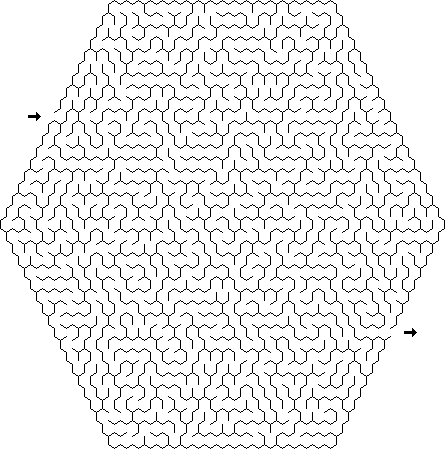
Sigma : Labirin Sigma terdiri dari segi enam terhubung; setiap sel dapat memiliki hingga enam lintasan.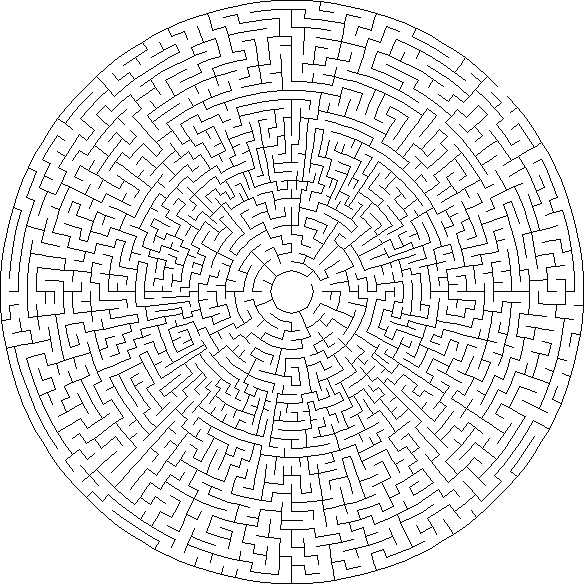
Theta : Labirin Theta terdiri dari lingkaran konsentris lorong-lorong di mana awal atau akhir berada di tengah dan yang lainnya di tepi luar. Sel biasanya memiliki empat jalur koneksi yang mungkin, tetapi mungkin ada lebih banyak karena lebih banyak sel di cincin luar lorong.
Epsilon : Labirin Epsilon terdiri dari octagons atau kuadrat yang terhubung, setiap sel di dalamnya dapat memiliki hingga delapan atau empat lintasan.
Zeta : Labirin zeta terletak di kotak persegi panjang, hanya di samping lorong horisontal dan vertikal, lorong diagonal diperbolehkan pada sudut 45 derajat.
Omega : istilah omega mengacu pada hampir setiap labirin dengan tessellation non-ortogonal yang konstan. Labirin delta, sigma, theta, dan ipsilon adalah dari jenis ini, seperti banyak skema lain yang dapat Anda pikirkan, misalnya, sebuah labirin yang terdiri dari pasangan segitiga siku-siku.
Retak : Labirin retak adalah labirin amorf tanpa penghentian konstan, di mana dinding dan jalur pejalan kaki terletak pada sudut acak.
Fraktal : Labirin fraktal adalah labirin yang terdiri dari labirin yang lebih kecil. Labirin fraktal dari sel bersarang adalah labirin di setiap sel tempat labirin lainnya ditempatkan, dan proses ini dapat diulang beberapa kali. Labirin fraktal rekursif tak terhingga adalah fraktal sejati di mana isi labirin mereplikasi dirinya sendiri, menciptakan labirin besar yang pada dasarnya tak terhingga.
Routing: Klasifikasi oleh routing mungkin merupakan aspek yang paling menarik dalam menghasilkan labirin. Dari dikaitkan dengan jenis lintasan dalam geometri yang didefinisikan dalam kategori yang dijelaskan di atas.

Ideal : "ideal" adalah labirin tanpa loop atau sirkuit tertutup dan tanpa area yang tidak terjangkau. Ini juga disebut Labirin yang terhubung sederhana. Dari setiap titik ada tepat satu jalur ke titik lain. Labirin hanya memiliki satu solusi. Dari sudut pandang pemrograman, labirin seperti itu dapat digambarkan sebagai pohon, sekumpulan sel atau simpul penghubung.
Jalinan : Jalinan berarti bahwa tidak ada jalan buntu di labirin. Ini juga disebut labirin labirin yang terhubung secara murni. Dalam labirin seperti itu, lorong-lorong digunakan sedekat itu dan kembali satu sama lain (karenanya disebut "anyaman"), mereka membuat mereka menghabiskan lebih banyak waktu berjalan dalam lingkaran daripada masuk ke jalan buntu. Labirin anyaman yang berkualitas bisa jauh lebih rumit daripada labirin ideal dengan ukuran yang sama.
Rute tunggal (Unicursal) : rute tunggal berarti labirin tanpa garpu. Labirin satu arah berisi satu lorong panjang berliku yang mengubah arah sepanjang labirin. Ini tidak terlalu rumit, hanya jika Anda tidak sengaja kembali setengah jalan dan tidak kembali ke awal.
Jarang: labirin jarang tidak melewati setiap sel, artinya, beberapa di antaranya tidak dibuat. Ini menyiratkan adanya daerah yang tidak terjangkau, yaitu, dalam arti, itu adalah kebalikan dari labirin anyaman. Konsep serupa dapat diterapkan ketika menambahkan dinding, sehingga Anda bisa mendapatkan labirin yang tidak rata dengan lorong dan kamar yang luas.- Parsial Wicker: Sebagian Wicker Maze adalah labirin campuran yang memiliki kedua loop dan jalan buntu. Kata "anyaman" dapat digunakan untuk penilaian kuantitatif, yaitu, "labirin dengan tenunan yang kuat" adalah labirin dengan banyak loop atau dinding dihilangkan, dan hanya ada beberapa di "labirin dengan tenun lemah".
Tekstur: klasifikasi
tekstur menjelaskan gaya lintasan dengan rute dan geometri yang berbeda. Tekstur bukan hanya parameter yang bisa dihidupkan atau dimatikan. Berikut ini beberapa contoh variabel:

Bias : dalam labirin dengan lorong-lorong yang bergeser, lorong lurus cenderung lebih ke satu arah daripada di yang lain. Misalnya, dalam labirin dengan perpindahan horisontal yang tinggi, kita akan memiliki lorong panjang dari kiri ke kanan, dan hanya lorong pendek dari atas ke bawah yang menghubungkannya. Labirin seperti itu biasanya lebih sulit untuk dilewati “melintasi serat”.
Overflight : Metrik Overflight menentukan berapa lama lorong akan diperlukan sebelum belokan paksa muncul. Dalam labirin dengan rentang rendah, tidak akan ada bagian lurus lebih lama dari tiga atau empat sel, dan itu akan terlihat sangat acak. Dalam labirin dengan rentang tinggi, labirin akan memiliki persentase lintasan panjang yang besar, yang akan membuatnya terlihat seperti microchip.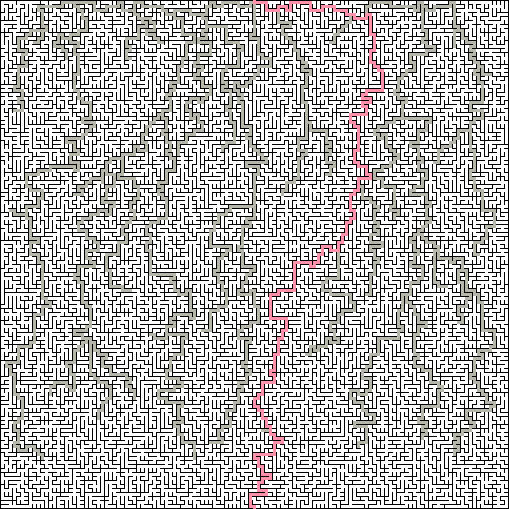
Elitisme: indikator "elit" dari labirin menentukan panjang solusi relatif terhadap ukuran labirin. Labirin elit biasanya memiliki solusi langsung yang pendek, sedangkan di labirin non-elit, solusi melewati sebagian besar area labirin. Labirin elit berkualitas tinggi bisa jauh lebih rumit daripada labirin non-elit.
Simetri : labirin simetris memiliki bagian simetris, misalnya, dalam simetri rotasi relatif ke pusat, atau tercermin sepanjang sumbu horizontal atau vertikal. Labirin dapat sebagian atau seluruhnya simetris, dan dapat mengulangi polanya beberapa kali.
Homogenitas: algoritma homogen menghasilkan semua labirin yang memungkinkan dengan probabilitas yang sama. Labirin dapat disebut memiliki tekstur homogen jika terlihat seperti labirin khas yang dihasilkan oleh algoritma homogen. Algoritma heterogen secara teoritis juga dapat menghasilkan semua labirin yang memungkinkan di ruang apa pun, tetapi tidak dengan probabilitas yang sama. Heterogenitas dapat melangkah lebih jauh - mungkin ada labirin yang tidak akan pernah dihasilkan oleh algoritma.- Aliran Sungai: Karakteristik "aliran" berarti bahwa ketika membuat labirin, algoritme akan mencari dan membersihkan sel-sel tetangga (atau dinding) ke sel saat ini, yaitu, ia akan mengalir (maka istilah "fluiditas") ke bagian labirin yang masih belum dibuat, seperti air. Dalam labirin ideal dengan laju aliran yang lebih rendah, biasanya akan ada banyak jalan buntu pendek, dan dalam labirin lebih "cair" akan ada lebih sedikit jalan buntu, tetapi mereka akan lebih lama.
Prioritas: klasifikasi ini menunjukkan bahwa proses pembuatan labirin dapat dibagi menjadi dua jenis utama: menambahkan dinding dan lorong ukiran. Biasanya, ketika membuat ini, hanya turun ke perbedaan dalam algoritma, dan tidak untuk perbedaan yang nyata dalam labirin, tetapi masih berguna untuk mempertimbangkan ini. Labirin yang sama sering dihasilkan dalam dua cara:
- Menambah dinding: Algoritma di mana dinding menjadi prioritas dimulai dengan area kosong (atau perbatasan eksternal), menambahkan dinding dalam proses. Di dunia nyata, labirin nyata yang terdiri dari pagar, langit-langit atau dinding kayu jelas menambah dinding.
- Pemotongan gang: Algoritma yang prioritasnya adalah gang mulai dengan blok padat dan memotong bagian di dalamnya dalam proses. Di dunia nyata, labirin seperti itu adalah terowongan tambang atau labirin di dalam pipa.

Templat: tentu saja, labirin dapat secara bersamaan memotong lorong dan menambahkan dinding; beberapa algoritma komputer melakukan itu. Templat labirin adalah gambar grafik yang bukan labirin, yang dalam beberapa langkah berubah menjadi labirin nyata, tetapi masih mempertahankan tekstur templat grafik asli. Gaya labirin yang kompleks, seperti berpotongan spiral, lebih mudah diimplementasikan sebagai pola di komputer, daripada mencoba membuat labirin yang tepat sambil mempertahankan gayanya.
Lainnya: yang di atas tidak berarti daftar lengkap dari semua kelas atau elemen yang mungkin dalam setiap kelas. Ini hanya tipe-tipe labirin yang saya buat sendiri. Perhatikan bahwa hampir setiap jenis labirin, termasuk labirin dengan aturan khusus, dapat dinyatakan sebagai grafik terarah, di mana akan ada jumlah negara hingga dan sejumlah pilihan hingga di setiap negara, dan ini disebut
kesetaraan labirin . Berikut adalah beberapa klasifikasi dan jenis labirin lainnya:

Orientasi : pada bagian-bagian tertentu Anda hanya dapat bergerak dalam satu arah. Dari sudut pandang pemrograman, labirin seperti itu akan dijelaskan oleh grafik berarah, berbeda dengan grafik tidak berarah yang menggambarkan semua jenis lainnya.
Segmentasi : labirin dapat memiliki bagian yang berbeda sesuai dengan kelas yang berbeda.
Labirin dengan panjang tak hingga: kita dapat membuat labirin panjang tak terhingga (sejumlah kolom dan jumlah baris terbatas), tetapi pada saat yang sama menyimpan hanya satu bagian dari labirin dalam memori, "menggulir" dari satu ujung ke ujung lainnya dan menghancurkan garis sebelumnya ketika membuat yang berikutnya. Salah satu contoh adalah versi modifikasi dari algoritma Hunt and Kill. Orang bisa membayangkan labirin yang tak berujung berpotensi dalam bentuk film panjang yang terdiri dari frame individu. Hanya dua frame berturut-turut yang disimpan dalam memori sekaligus. Mari kita jalankan algoritma Hunt and Kill, meskipun itu menciptakan bias yang cenderung ke frame atas, jadi itu berakhir dulu. Setelah selesai, bingkai tidak lagi diperlukan, Anda dapat mencetaknya atau melakukan hal lain dengannya. Namun, buanglah, buat frame bawah yang baru dibuat sebagian menjadi frame atas baru dan kosongkan frame bawah yang baru. Ulangi proses ini sampai kami memutuskan untuk berhenti, dan kemudian menunggu sampai Hunt And Kill menyelesaikan kedua frame. Satu-satunya batasan adalah bahwa labirin tidak akan pernah memiliki jalan bercabang menuju pintu masuk untuk panjang lebih dari dua bingkai. Cara termudah untuk membuat labirin tak berujung adalah algoritma Eller atau algoritma Sidewinder, karena mereka sudah membuat labirin satu baris pada satu waktu, sehingga Anda bisa membiarkan mereka menambahkan baris tanpa akhir ke labirin.
Virtual labirin fraktal: virtual adalah labirin di mana seluruh labirin tidak disimpan dalam memori pada saat yang sama. Misalnya, itu hanya dapat menyimpan bagian dari lorong 100x100 di dekat lokasi Anda dalam simulasi tempat Anda berjalan melalui labirin besar. Perpanjangan labirin fraktal bersarang dapat digunakan untuk membuat labirin virtual yang sangat besar, misalnya, satu miliar per miliar lintasan. Jika kita membuat salinan nyata labirin dari satu miliar per miliar lintasan (dengan jarak enam kaki di antara lintasan), maka itu akan memenuhi permukaan bumi lebih dari 6.000 kali! Pertimbangkan sebuah labirin dengan 10 9 hingga 10 9 lintasan, atau sebuah labirin tertutup dengan hanya 9 tingkat. Jika kita ingin memiliki setidaknya 100x100 bagian di sekitar kita, maka cukup bagi kita untuk membuat pada level terendah sub labirin 100x100 lintasan dan tujuh 10x10 labirin di mana ia tertanam untuk mengetahui dengan tepat di mana dinding berada di dalam bagian 100x100. (Sebenarnya, lebih baik memiliki empat bagian yang berdekatan berukuran 100x100, membentuk bujur sangkar jika Anda berada di dekat tepi atau sudut bagian tersebut, tetapi konsep yang sama berlaku di sini.) Untuk memastikan labirin konstan dan tidak berubah ketika bergerak di sekitarnya, kami memiliki rumus, mendefinisikan nomor benih acak untuk setiap koordinat di setiap tingkat bersarang. Labirin fraktal virtual mirip dengan fraktal Mandelbrot, dalam gambar yang memang ada, dan kita perlu mengunjungi koordinat tertentu dengan perbesaran yang cukup tinggi. sehingga muncul.
Algoritma Labirin
Berikut adalah daftar algoritma umum untuk membuat berbagai kelas labirin yang dijelaskan di atas:

Ideal : untuk membuat labirin ideal standar, biasanya perlu “menumbuhkannya”, memastikan tidak adanya loop dan area yang terisolasi. Kami mulai dari dinding luar dan secara acak menambahkan fragmen dinding yang menyentuhnya. Kami terus menambahkan segmen dinding secara acak ke labirin, tetapi pastikan bahwa setiap segmen baru menyentuh dari satu ujung dinding yang ada, dan ujung lainnya berada di bagian labirin yang masih belum dibuat. Jika Anda menambahkan segmen dinding, kedua ujungnya dipisahkan dari sisa labirin, maka ini akan membuat dinding yang tidak terhubung dengan lingkaran di sekitarnya, dan jika Anda menambahkan segmen, kedua ujungnya menyentuh labirin, ini akan membuat area yang tidak terjangkau. Ini adalah metode penambahan dinding; hampir analog dengan memotong bagian-bagian, di mana bagian-bagian bagian dipotong sehingga hanya satu ujung yang menyentuh bagian yang ada.
: , , . : (1) , (2) , , -«», (3) , , , (4) , , (3) , , .
: — , , , , . U- , , , , . . , : , , , . , . , .
: , . , , . - , , , , .- 3D : , , , . - .

: , , . ( ): , , , . , . , ; , . , , .
Crack : Crack- , , . , , , «» . , , . , - . , , ; . , .
: «» , , . , - : (1) , . (2) , , , , , (.. ). (3) , , . , .
: — 3D-, -, , . 3D- , , . , , . , . , ( ), , , .
Planair : Planair- , . — . , .
: , , , -, , , , . , . , , , , , .
Ada banyak cara untuk membuat labirin yang sempurna, dan masing-masing memiliki karakteristiknya sendiri. Di bawah ini adalah daftar algoritma spesifik. Semua dari mereka menggambarkan penciptaan labirin dengan memotong jalan, namun, kecuali dinyatakan sebaliknya, masing-masing juga dapat diimplementasikan dengan menambahkan dinding:
Backtracker rekursif : - recursive backtracker, , . , , . , , . , . , . , , , . , . Recursive backtracking , , , .
: , . , «» , , . , , ( ). , . , , . , - , , . , , . , . , - (union-find algorithm): , . . , - .
Algoritma Prima (benar) : Algoritma ini menciptakan pohon rentang minimum dengan memproses bobot tepi acak yang unik. Jumlah memori yang dibutuhkan sebanding dengan ukuran labirin. Kita mulai dari titik mana pun (labirin jadi akan sama, tidak peduli dari atas kita mulai). Kami memilih tepi lorong dengan bobot terkecil yang menghubungkan labirin ke titik yang belum ada di dalamnya, dan kemudian menempelkannya ke labirin. Labirin selesai ketika ujung-ujungnya tidak lagi tersisa. Untuk memilih tepi berikutnya secara efisien, Anda memerlukan antrian prioritas (biasanya diimplementasikan menggunakan heap) yang menyimpan semua tepi perbatasan. Namun, algoritma ini agak lambat karena butuh log (n) waktu untuk memilih item dari heap. Oleh karena itu, lebih baik untuk memilih algoritma Kraskal, yang juga membuat pohon spanning minimal, karena lebih cepat dan menciptakan labirin dengan struktur yang identik. Faktanya, dengan seed acak yang sama, algoritma Prima dan Kraskal dapat membuat labirin yang sama.
Algoritma Prim (Sederhana) : Algoritma Prim ini membuat pohon spanning minimal. Ini disederhanakan sedemikian rupa sehingga semua bobot tepi adalah sama. Ini membutuhkan kapasitas memori sebanding dengan ukuran labirin. Kami mulai dari puncak acak. Kami secara acak memilih tepi lorong yang menghubungkan labirin dengan titik yang belum ada di dalamnya, dan kemudian menempelkannya ke labirin. Labirin selesai ketika ujung-ujungnya tidak lagi tersisa. Karena tepinya tidak berbobot dan tidak dipesan, maka dapat disimpan sebagai daftar sederhana, yaitu pemilihan elemen dari daftar akan sangat cepat dan membutuhkan waktu yang konstan. Oleh karena itu, ini jauh lebih cepat daripada algoritma Prim sejati dengan bobot tepi acak. Tekstur labirin yang dibuat akan memiliki indeks hasil lebih rendah dan solusi yang lebih sederhana daripada algoritma Prima yang sebenarnya, karena menyebar dari titik awal secara merata, seperti sirup yang tumpah, dan tidak mem-bypass fragmen tulang rusuk dengan bobot lebih tinggi, yang diperhitungkan kemudian.
Algoritma Prim (dimodifikasi) : Algoritma Prim ini membuat pohon spanning minimal, dimodifikasi sehingga semua bobot tepi adalah sama. Namun, ini diterapkan sedemikian rupa sehingga alih-alih tepi itu melihat sel. Jumlah memori sebanding dengan ukuran labirin. Dalam proses penciptaan, setiap sel dapat memiliki satu dari tiga jenis: (1) "internal": sel adalah bagian dari labirin dan sudah dipotong di dalamnya, (2) "batas": sel bukan bagian dari labirin dan belum dipotong di dalamnya, tetapi terletak di sebelah sel yang sudah "internal", dan (3) "eksternal": sel belum menjadi bagian dari labirin, dan tidak ada tetangganya yang juga sel "internal". Kami mulai dengan memilih sel, menjadikannya "internal", dan untuk semua tetangganya kami menyetel jenisnya menjadi "batas". Kami secara acak memilih sel "batas" dan memotong satu bagian dari salah satu sel "internal" di sekitarnya. Kami mengubah status sel "batas" ini menjadi "internal" dan mengubah jenis semua tetangganya dari "eksternal" menjadi "perbatasan". Labirin diselesaikan ketika tidak ada lagi sel "batas" yang tersisa (yaitu, tidak ada sel "eksternal" yang tersisa, yang berarti bahwa setiap orang telah menjadi "internal"). Algoritma ini menciptakan labirin dengan indeks hasil yang sangat rendah, memiliki banyak deadlock pendek dan solusi yang lebih mudah. Labirin yang dihasilkan sangat mirip dengan hasil dari algoritma Prima yang disederhanakan, dengan sedikit perbedaan: void dalam spanning tree diisi hanya jika sel batas dipilih secara acak, berbeda dengan probabilitas tiga kali lipat untuk mengisi sel ini melalui salah satu sel batas yang mengarah ke sana. Selain itu, algoritma ini sangat cepat, lebih cepat daripada algoritma Prim yang disederhanakan, karena tidak perlu mengkompilasi dan memproses daftar edge.
Algoritma Aldous-Broder : apa yang menarik dalam algoritma ini adalah bahwa itu homogen, yaitu, ia menciptakan dengan probabilitas yang sama semua labirin yang mungkin dari ukuran yang diberikan. Selain itu, tidak memerlukan memori atau tumpukan tambahan. Kami memilih titik dan secara acak pindah ke sel tetangga. Jika kita masuk ke sel yang belum dipotong, maka potong bagian dari sel sebelumnya ke dalamnya. Kami terus bergerak ke sel tetangga sampai kami memotong bagian ke semua sel. Algoritma ini menciptakan labirin dengan laju aliran rendah, hanya sedikit lebih tinggi dari algoritma Kraskal. (Ini berarti bahwa untuk pertukaran yang diberikan, ada lebih banyak labirin dengan indeks hasil rendah daripada dengan yang tinggi, karena labirin dengan probabilitas rata-rata sama rendahnya.) Hal buruk tentang algoritma ini adalah sangat lambat karena tidak melakukan pencarian intelektual untuk yang terakhir. sel, yaitu, pada kenyataannya, tidak memiliki jaminan penyelesaian. Namun, karena kesederhanaannya, ia dapat dengan cepat melewati banyak sel, sehingga selesai lebih cepat dari yang Anda kira. Rata-rata, dibutuhkan tujuh kali lebih lama untuk menyelesaikan daripada algoritma standar, meskipun dalam kasus yang buruk bisa lebih lama jika generator angka acak terus-menerus menghindari beberapa sel terakhir. Ini dapat diimplementasikan sebagai dinding tambahan, jika dinding perbatasan dianggap sebagai simpul tunggal, mis., Misalnya, jika memindahkan kita ke dinding perbatasan, kita akan berteleportasi ke titik acak di sepanjang perbatasan, dan hanya kemudian terus bergerak. Dalam hal penambahan dinding, ia bekerja hampir dua kali lebih cepat, karena teleportasi di sepanjang dinding perbatasan memungkinkan akses yang lebih cepat ke bagian-bagian labirin yang jauh.
Algoritma Wilson : ini adalah versi perbaikan dari algoritma Aldous-Broder, ini menciptakan labirin dengan tekstur yang persis sama (algoritmanya homogen, artinya, semua labirin yang mungkin dihasilkan dengan probabilitas yang sama), tetapi algoritma Wilson jauh lebih cepat. Perlu memori hingga ukuran labirin. Kami mulai dengan sel labirin awal yang dipilih secara acak. Kami memilih sel acak yang belum menjadi bagian dari labirin dan melakukan jalan acak hingga kami menemukan sel yang sudah dimiliki labirin. Segera setelah kita menemukan bagian labirin yang telah dibuat, kita kembali ke sel acak yang dipilih dan memotong seluruh jalur yang dilakukan dengan menambahkan sel-sel ini ke labirin. Lebih khusus lagi, ketika kita kembali di sepanjang jalan, kita memotong di setiap sel ke arah di mana berjalan acak terjadi terakhir kali kita meninggalkan sel. Ini menghindari tampilan loop di sepanjang jalan kembali, sehingga satu bagian panjang bergabung dengan labirin. Labirin selesai ketika semua sel melekat padanya. Algoritme memiliki masalah kecepatan yang sama dengan Aldous-Broder, karena dapat memakan waktu lama untuk menemukan jalur acak pertama ke sel awal, tetapi setelah menempatkan beberapa jalur, sisa labirin dipotong cukup cepat. Rata-rata, ini berjalan lima kali lebih cepat dari Aldous-Broder, dan kurang dari dua kali lebih lambat dari algoritma terbaik. Perlu dipertimbangkan bahwa dalam kasus penambahan dinding, ia bekerja dua kali lebih cepat, karena seluruh dinding perbatasan awalnya merupakan bagian dari labirin, sehingga dinding pertama bergabung lebih cepat.
Algoritma berburu dan membunuh : algoritma ini mudah digunakan karena tidak memerlukan memori tambahan atau tumpukan, dan karenanya cocok untuk membuat labirin besar atau labirin pada komputer yang lemah karena ketidakmungkinan kehabisan memori. Karena tidak memiliki aturan yang harus diikuti terus-menerus, ia juga paling mudah untuk memodifikasi dan membuat labirin dengan tekstur berbeda yang menggunakannya. Ini hampir mirip dengan backtracker rekursif, hanya saja tidak ada sel yang tidak dibuat di dekat posisi saat ini. Kami memasuki mode "berburu" dan memindai labirin secara sistematis hingga kami menemukan sel yang belum dibuat di sebelah sel yang sudah dipotong. Pada tahap ini, kami kembali mulai memotong di lokasi baru ini. Labirin selesai ketika dalam mode "berburu" semua sel dipindai. Algoritma ini cenderung membuat labirin dengan laju aliran tinggi, tetapi tidak setinggi backtracker rekursif. Anda dapat memaksanya untuk menghasilkan labirin dengan laju aliran yang lebih rendah, lebih sering memasuki mode "berburu". Ini berjalan lebih lambat karena waktu yang dihabiskan untuk berburu sel terakhir, tetapi tidak jauh lebih lambat daripada algoritma Kraskal. Ini dapat diimplementasikan sesuai dengan prinsip menambahkan dinding, jika Anda sesekali teleport secara acak untuk menghindari masalah yang melekat pada backtracker rekursif.
Algoritma yang berkembang
tree (Growing tree algorithm) : ini adalah algoritma umum yang dapat membuat labirin dengan tekstur yang berbeda. Memori yang dibutuhkan dapat mencapai ukuran labirin. Setiap kali sel dipotong, kami menambahkannya ke daftar. Pilih sel dari daftar dan potong bagian ke sel yang tidak dibuat di sebelahnya. Jika tidak ada sel yang belum dibuat di dekat yang sekarang, hapus sel saat ini dari daftar. Labirin selesai ketika tidak ada yang lain dalam daftar. Hal yang menarik tentang algoritme adalah bahwa, tergantung pada bagaimana Anda memilih sel dari daftar, Anda dapat membuat banyak tekstur yang berbeda. Misalnya, jika Anda selalu memilih sel yang ditambahkan terakhir, maka algoritme ini berubah menjadi pelacak mundur rekursif. Jika Anda selalu memilih sel secara acak, maka berperilaku serupa, tetapi tidak identik dengan algoritma Prim. Jika Anda selalu memilih sel tertua yang ditambahkan ke daftar, maka kami akan membuat labirin dengan indeks hasil serendah mungkin, bahkan lebih rendah dari pada algoritma Prim. Jika Anda biasanya memilih sel terakhir, tetapi sesekali memilih sel acak, maka labirin akan memiliki laju aliran tinggi, tetapi solusi singkat dan langsung. Jika salah satu sel terbaru dipilih secara acak, labirin akan memiliki laju aliran rendah, tetapi solusi yang panjang dan berliku.
Algoritma hutan tumbuh : Ini adalah algoritma yang lebih umum menggabungkan jenis berdasarkan pohon dan set. Ini adalah perpanjangan dari algoritma pertumbuhan pohon, yang pada dasarnya mencakup beberapa contoh yang berkembang secara bersamaan. Kami mulai dengan semua sel yang diurutkan secara acak ke dalam daftar "baru"; Selain itu, setiap sel memiliki set sendiri, seperti pada awal algoritma Kruskal. Pertama, pilih satu atau lebih sel dengan memindahkannya dari daftar "baru" ke daftar "aktif". Pilih sel dari daftar "aktif" dan hilangkan bagian ke sel yang tidak dibuat berikutnya dari daftar "baru", menambahkan sel baru ke daftar "aktif" dan menggabungkan set dua sel. Jika suatu upaya dilakukan untuk memotong bagian labirin yang ada, maka aktifkan jika sel-sel berada di set yang berbeda dan menggabungkan sel-sel, seperti yang dilakukan dalam algoritma Kraskal. Jika tidak ada sel "baru" di dekat sel saat ini, maka pindahkan sel saat ini ke daftar yang "selesai". Labirin selesai ketika daftar "aktif" menjadi kosong. Pada akhirnya, kami menggabungkan semua set yang tersisa, seperti pada algoritma Kruskal. Secara berkala, Anda dapat membuat pohon baru dengan memindahkan satu atau lebih sel dari daftar "baru" ke daftar "aktif", seperti yang dilakukan di awal. Dengan mengontrol jumlah pohon asli dan bagian dari pohon yang baru dibuat, Anda dapat menghasilkan banyak tekstur unik yang digabungkan dengan parameter yang sudah fleksibel dari algoritma penanaman pohon.
Algoritma Eller : ini adalah algoritma khusus, karena tidak hanya lebih cepat dari yang lain, tetapi juga tidak memiliki bias atau kekurangan yang jelas; selain itu, ketika dibuat, memori digunakan paling efisien. Bahkan tidak mengharuskan seluruh labirin ada di memori, ia menggunakan volume yang proporsional dengan ukuran garis. Ini menciptakan garis labirin demi baris, setelah generasi string selesai, algoritma tidak lagi memperhitungkannya. Setiap sel dalam satu baris terkandung dalam satu set; dua sel milik set yang sama jika ada jalur di antara mereka di sepanjang labirin yang sudah dibuat. Informasi ini memungkinkan Anda untuk memotong bagian-bagian di jalur saat ini tanpa membuat loop atau area yang terisolasi. Bahkan, ini sangat mirip dengan algoritma Kraskal, hanya di sini ia dibentuk satu baris pada satu waktu, sementara Kraskal melihat melalui seluruh labirin. Membuat baris terdiri dari dua bagian: sambungkan sel yang berdekatan secara acak di dalam baris, mis. kita memotong bagian horisontal, lalu secara acak menghubungkan sel-sel antara arus dan baris berikutnya, mis. memotong bagian vertikal. Saat memotong bagian horisontal, kita tidak menghubungkan sel yang sudah ada di set yang sama (karena loop akan dibuat sebaliknya), dan ketika memotong bagian vertikal kita harus menghubungkan sel jika memiliki ukuran satuan (karena jika Anda meninggalkannya, itu akan membuat area yang terisolasi). Saat memotong bagian horisontal, kami menghubungkan sel jika mereka berada di set yang sama (karena sekarang ada jalur di antara mereka), dan ketika memotong bagian vertikal ketika kami tidak terhubung dengan sel, kami meletakkannya di set yang terpisah (karena sekarang dipisahkan dari sisa labirin) ) Penciptaan dimulai dengan fakta bahwa sebelum menghubungkan sel-sel di baris pertama, setiap sel memiliki set sendiri. Pembuatan selesai setelah sel terhubung di baris terakhir. Ada aturan khusus penyelesaian: pada saat selesai, masing-masing sel harus dalam set yang sama untuk menghindari daerah yang terisolasi. (Baris terakhir dibuat dengan menggabungkan masing-masing pasangan sel tetangga yang belum dalam set yang sama.) Yang terbaik untuk mengimplementasikan set menggunakan daftar sel yang saling terkait secara siklik (yang bisa berupa array yang mengikat sel ke pasangan sel di kedua sisi set yang sama), memungkinkan melakukan penyisipan, penghapusan dan verifikasi keberadaan sel tetangga dalam satu set untuk waktu yang konstan. Masalah dengan algoritma ini adalah ketidakseimbangan dalam memproses tepi yang berbeda dari labirin; Untuk menghindari noda pada tekstur, Anda perlu menghubungkan dan melewati sel penghubung dalam proporsi yang benar.
Pembagian rekursif: algoritma ini agak mirip dengan backtracking rekursif, karena mereka berdua menggunakan tumpukan, hanya bekerja tidak dengan lorong, tetapi dengan dinding. Kita mulai dengan membuat dinding horizontal atau vertikal acak yang memotong area yang dapat diakses dalam baris atau kolom acak, dan secara acak menempatkan ruang kosong di sepanjang itu. Kemudian kami mengulangi proses secara rekursif untuk dua subregional yang dihasilkan oleh dinding pemisah. Untuk hasil terbaik, Anda perlu menambahkan penyimpangan dalam pilihan horizontal atau vertikal berdasarkan proporsi area, misalnya, area yang lebarnya dua kali tingginya harus lebih sering dibagi dengan dinding vertikal. Ini adalah algoritme tercepat tanpa penyimpangan arah, dan seringkali dapat bersaing dengan labirin yang didasarkan pada pohon biner, karena ia menciptakan beberapa sel pada saat yang sama, meskipun ia memiliki kelemahan yang jelas dalam bentuk dinding panjang yang memotong interior labirin. Algoritma ini adalah semacam labirin fraktal yang tertanam, tetapi alih-alih secara konstan membuat labirin sel dengan ukuran tetap dengan labirin dengan ukuran yang sama di dalam setiap sel, algoritma ini secara acak membagi area tertentu menjadi labirin ukuran acak: 1x2 atau 2x1. Pembagian rekursif tidak dapat digunakan untuk memotong bagian-bagian, karena ini mengarah pada penciptaan solusi yang jelas yang mengikuti sepanjang tepi luar, atau sebaliknya langsung memotong bagian dalam.
Labirin yang didasarkan pada pohon biner : sebenarnya, ini adalah algoritma yang paling sederhana dan tercepat, namun, labirin yang dibuat memiliki tekstur dengan bias yang sangat tinggi. Untuk setiap sel, kami memotong bagian baik ke atas atau ke kiri, tetapi tidak pernah di kedua arah. Dalam versi dengan penambahan dinding, segmen dinding ditambahkan untuk setiap titik mengarah ke bawah atau ke kanan, tetapi tidak di kedua arah. Setiap sel independen dari semua sel lain, karena kita tidak perlu memeriksa keadaan beberapa sel lain saat membuatnya. Oleh karena itu, ini adalah algoritma nyata untuk menghasilkan labirin tanpa memori, tidak dibatasi oleh ukuran labirin yang dibuat. Sebenarnya, ini adalah pohon biner, jika kita menganggap sudut kiri atas sebagai root, dan setiap simpul atau sel memiliki satu simpul induk unik, yang merupakan sel di atas atau di sebelah kiri darinya. Labirin yang didasarkan pada pohon biner berbeda dari labirin ideal standar, karena lebih dari setengah jenis sel tidak dapat ada di dalamnya. Sebagai contoh, tidak akan pernah ada persimpangan di dalamnya, dan semua jalan buntu memiliki bagian mengarah ke atas atau ke kiri, dan tidak pernah mengarah ke bawah atau ke kanan. Labirin cenderung memiliki lorong-lorong yang mengarah secara diagonal dari kiri atas ke kanan bawah, dan jauh lebih mudah untuk bergerak dari kanan bawah ke kiri atas. Anda selalu dapat bergerak ke atas atau ke kiri, tetapi tidak pernah secara bersamaan di kedua arah, sehingga Anda selalu dapat bergerak secara deterministik diagonal ke atas dan ke kiri, tanpa menemui hambatan. Anda akan memiliki kesempatan untuk memilih dan jatuh ke jalan buntu dengan bergerak ke bawah dan ke kanan. , , , .
Sidewinder: , . : , , . , , , , , . , ( , ). , sidewinder . , sidewinder . , sidewinder , , . sidewinder , « ». , sidewinder — , , , , . sidewinder , , , .
| % | | | ? | ? | | | % |
| 0 | | | | | N^2 | 379 | 100.0 |
| Recursive Backtracker | 10 | | | | | N^2 | 27 | 19.0 |
| Hunt and Kill | 11 (21) | | | | | 0 | 100 (143) | 9.5 (3.9) |
| 23 | | | | | N* | 10 | 7.2 |
| 25 | | | | | 0* | 10 | 2.0 |
| Sidewinder | 27 | | | | | 0* | 12 | 2.6 |
| 28 | | | | | N* | 20 | 4.2 (3.2) |
| Tanggal 29 | | | | | N^2 | 48 (25) | 4.5 |
| - | Tanggal 29 | | | | | 0 | 279 (208) | 4.5 |
| 30 | | | | | N^2 | 33 | 4.1 |
| () | 30 | | | | | N^2 | 160 | 4.1 |
| () | 32 | | | | | N^2 | 59 | 2.3 |
| () | 36 (31) | | | | | N^2 | 30 | 2.3 |
| 49 (39) | | | | | N^2 | 48 | 11.0 |
| 49 (39) | | | | | N^2 | 76 | 11.0 |
Tabel ini merangkum karakteristik algoritma untuk membuat labirin ideal yang dijelaskan di atas. Sebagai perbandingan, algoritma labirin rute tunggal telah ditambahkan (secara teoritis, labirin rute tunggal ideal). Penjelasan kolom:- : , , , 2D-. . , , , . 10% ( ) 49% ( ). Recursive Backtracker 1%. 66%: .
- : : , , . , , , , . , , .
- : , . . , , . Recursive Backtracker , , , . , , . , Hunt and Kill , , .
- : , . , . Sidewinder , . , . Hunt and Kill , , , .
- : . «» , . «» , , . «» , , . , .
- : , . , , (N), (N^2). , ( ). , , . Sidewinder , . , .
- : , , , . , ( 10), . 100x100 Daedalus. , , , .
- : , , . , 100x100 . . «» . , . , . , , , .
Ada banyak cara untuk mengatasi labirin, dan masing-masing memiliki karakteristik sendiri. Berikut adalah daftar algoritma tertentu:
Mengikuti sepanjang dinding (Pengikut dinding) : . («»), . ( ). , ( ) . , . , , . , , , . 3D- , 3D- 2D-, .. , -, -, .
: , «» , . 2D- , , .. . , , . . , , . , , . , , . , , — -1, — 1. , , .. 360 , «». , «», , , , , . , , . , — , .
: (Chain algorithm) , ( ) . , , . , . , , . , . ( ) , . . , , . «» , . , , , . , . , .
Recursive backtracker: , . , . : ( ), «», , , «», , . , , «»; «» . (backtracking) , , . , . , , .
(Trémaux's algorithm): . recursive backtracker : , . , . , , . , , , . ( , .) , (.. ), , , , (.. , ). , , , , , . , . , , .
(Dead end filler) : . , . , , . , . , , . , , .
Cul-de-sac filler : , , . dead end filler, , . ( — , , ) , . dead end filler. , , , , . , , , dead end filler.
Blind alley filler : , , . , . — , , . , , cul-de-sac filler, . . , , , , . , , , ( ). , , . , cul-de-sac filler - , collision solver , - .
Blind alley sealer : blind alley filler , , . . . , , blind alley filler, . . , , , , . , , . , . , , . , , .
(Shortest path finder): , , . , , . collision solver, , , «» , ( ), «» , , . «», , . , - , . , , , A* , .
(Shortest paths finder) : , . , , , , , , , - , . , , , «» , , , . , , , , . , .- Collision solver: "amoeba" solver. . , . «» , ( ). « » ( ), , . «», , , , . ( , «», . , , , .) , shortest paths finder, ( ) ( ).
- Random mouse: , , .. , . 180 , . , , . , , .
| | ? | | ? | ? | ? | ? |
| Random Mouse | 1 | | | / | | | |
| Wall Follower | 1 | | | / | | | |
| 1 | | | / | | | |
| 1 | | + | | | | |
| Backtracker rekursif | 1 | Ya | Kamu adalah | Tidak | Ya | Tidak | Ya |
| Algoritma Tremo | 1 | Ya | Kamu adalah | Di dalam / di atas | Tidak | Tidak | Ya |
| Pengisi buntu | Semua + | Tidak | Labirin | Berakhir | Tidak | Ya | Ya |
| Pengisi kul-de-sac | Semua + | Tidak | Labirin | Berakhir | Tidak | Ya | Ya |
| Sealer lorong buta | Semua + | Ya | Labirin | Tidak | Tidak | Tidak | Ya |
| Pengisi lorong buta | Semua | Ya | Labirin | Berakhir | Tidak | Ya | Tidak |
| Pemecah tabrakan | Semua yang terpendek | Ya | Anda + | Tidak | Tidak | Tidak | Ya |
| Cari jalur terpendek | Semua yang terpendek | Ya | Anda + | Tidak | Ya | Tidak | Ya |
| Cari jalur terpendek | 1 terpendek | Ya | Anda + | Tidak | Ya | Tidak | Ya |
Tabel ini secara singkat mencantumkan karakteristik algoritma penyelesaian labirin yang dijelaskan di atas. Menurut kriteria ini, dimungkinkan untuk mengklasifikasikan dan mengevaluasi algoritma untuk memecahkan labirin. Penjelasan Kolom:- : , . . , () . Dead end filler cul-de-sac filler ( blind alley sealer ) , , , «+».
- : . Random mouse «», , wall follower «», , . dead end filler cul-de-sac filler «», .
- : : «» ( ) . , ( «») («+») . , .
- : , , . , «», , ( ), , , , . .
- : . , , , , . Wall follower, . Recursive backtracker shortest path(s) finder .
- : . .
- Cepat: Apakah proses pengambilan keputusan dianggap cepat. Algoritma yang paling efisien cukup untuk melihat setiap sel labirin hanya sekali, atau mereka dapat sepenuhnya melewati bagian-bagiannya. Runtime harus proporsional dengan ukuran labirin, atau O (n ^ 2), di mana n adalah jumlah sel di satu sisi. Mouse acak lambat karena penyelesaiannya tidak dijamin, dan pengisi jalan buntu berpotensi memecahkan labirin dari setiap garpu.
Operasi lain dengan labirin
Selain membuat dan menyelesaikan labirin, Anda dapat melakukan operasi lain dengannya:
: « », , Fill FloodFill. FloodFill , , . , , FloodFill , . , , FloodFill , , . «» .
(Isolation remover): , , . , . , . ( , ) , . , , . .
: , , . , , . , . ( , ) . , , , . , .
: , . , , , , . , , . , . , blind alley sealer ( , ). , , .
- Daedalus : Daedalus, Windows. Daedalus .