Gugologi (ini bukan kesalahan ketik) untuk programmer

Lebih sulit untuk menulis tentang matematika (sehingga menarik) daripada tentang fisika. Namun, saya harap Anda membaca setidaknya contoh program C gila.


Monster bisa tumbuh dari hal-hal yang sama sekali tidak berbahaya. Ambil, misalnya, permainan substring. Kami menulis string huruf a dan b dan memilih substring dari karakter 1 ke karakter 2, dari 2 hingga 4, dari tiga menjadi 6, dari n hingga 2n, hingga panjang string utama sudah cukup. Tugas kita adalah memastikan bahwa dalam substring ini yang lebih pendek tidak masuk ke dalam lagi. Saya bahkan menulis parser SQL:

declare @s varchar(max) = 'abbbaaaaaaab' declare @n int=1 declare @sub table (n int, sub varchar(max)) while @n*2<=len(@s) begin insert into @sub select @n,substring(@s,@n,@n+1) set @n=@n+1 end select *,(select max(sub) from @sub I where In>On and charindex(O.sub,I.sub)>0) as FoundMatch from @sub O order by 1 

Berikut adalah contoh output:



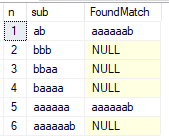
Seperti yang Anda lihat, substring 1 dan 5 tidak lulus tes. Kita dapat menghapus karakter terakhir, dan string 11 karakter yang dihasilkan 'abbbaaaaaaaa' akan lulus ujian. Ternyata ini adalah string terpanjang yang mungkin dalam alfabet dua karakter yang memenuhi kondisi ini.

Untuk alfabet satu karakter, panjang string maksimum adalah 3, dan kemudian karena alasan teknis semata. Ternyata panjang maksimalnya terbatas untuk alfabet sejumlah huruf. Jadi kita punya:

$$

$$f (1) = 3$$

$$

$$f (2) = 11$$

$$

$$f (3) = ???$$

Uji intuisi Anda tentang berapa lama string dapat dibuat dalam alfabet tiga huruf. 100? 1000? Bahkan, lebih dari Googol, dan lebih dari GoogolPlekh.

$$

$$f (3)> 2 \ uparrow ^ {7198} 158836$$

Dan saya harus menghabiskan waktu untuk menunjukkan kekuatan para penembak.

Panah (hiperoperasi)

Kami menggunakan perkalian agar tidak menulis banyak operasi tambahan:

$$

$$2 * 5 = 2 + 2 + 2 + 2 + 2$$

Kami menggunakan eksponensial agar tidak menulis banyak perkalian:

$$

$$2 ^ 3 = 2 * 2 * 2$$

Mempertimbangkan penambahan sebagai operasi level 0, perkalian sebagai 1, eksponensial sebagai 2, kita dapat memperkenalkan operasi "panah", misalnya,

$$

$$3 \ uparrow 3 = 3 ^ {(3 ^ 3)} = 3 ^ {27} = 7'625'597'484'987$$

Perhatikan bahwa tanda kurung sudah penting di sini. Level selanjutnya adalah operasi dua panah:

$$

$$3 \ uparrow \ uparrow 3 = 3 \ uparrow (3 \ uparrow 3) = 3 \ uparrow 7625597484987 = 3 ^ {3 ^ {... ^ 3}}$$

Piramida tiga kali lipat terakhir memiliki ketinggian 7 miliar, dan jumlah ini sudah jauh, jauh lebih besar daripada googol dan googolpleks. Kami menyatakan angka yang sangat besar ini sebagai Kegelapan (itu adalah angka dalam bahasa Rusia lama) dan mencoba untuk mengambil satu langkah lagi:

$$

$$3 \ uparrow ^ 3 3 = 3 \ uparrow \ uparrow \ uparrow 3 = 3 \ uparrow \ uparrow (3 \ uparrow \ uparrow 3) = 3 \ uparrow \ uparrow {darkness} = 3 \ uparrow 3 \ uparrow 3 ... \ uparrow 3$$

(Dan berkali-kali) ... Bahkan sudah ada yang membayangkan seberapa besar angka ini. Harap dicatat bahwa ketika ada banyak panah, kami menulis repeater di bagian atas. Jadi Anda bisa mengerti betapa hebatnya

$$

$$f (3)> 2 \ uparrow ^ {7198} 158836$$

Dan lagi

Dengan menggunakan panah, hanya angka terkecil dari jumlah besar yang dibuat. Tingkat pertumbuhan fungsi diukur pada skala tertentu - dengan membandingkan dengan fungsi yang tumbuh cepat . Fungsi pertama dalam hierarki ini terkait dengan penjumlahan, yang kedua ke perkalian, yang ketiga ke panah, dan panah ke-n ke ke-2 (kira-kira, tidak persis). Tapi Anda bisa mendefinisikan

$$

$$f_w (n) = f_n (n)$$

Fungsi seperti untuk n = 3 dapat dibandingkan dengan satu panah, untuk n = 4 dengan dua panah, dan ketika parameter n tumbuh, itu melampaui pertumbuhan fungsi dengan jumlah panah statis.

Anda dapat melangkah lebih jauh: $$$f_w, f_ {w + 1}, f_ {w + n}, f_ {w2}, f_ {w ^ 2}, f_ {w ^ w}, f_ {w ^ {w ^ {w}}}}, f_ \ epsilon$ Fungsi-fungsi ini diindeks oleh ordinal, atau dalam literatur Rusia dengan nomor urut. Gambar dengan struktur bilangan ordinal awal mendahului artikel, tetapi mereka memperpanjang lebih jauh, dan selanjutnya dimulai

Mistisisme kecil

Piramida omega yang tak ada habisnya memberikan ordinal $$$\ epsilon_0$ . Baca tentang fungsi yang pertumbuhannya diukur dengan ordinal ini. Ternyata suatu fungsi tumbuh begitu cepat sehingga aritmatika formal pada prinsipnya tidak dapat membuktikan bahwa fungsi semacam itu didefinisikan sama sekali!

Tentu saja, Anda tahu tentang teorema Godel bahwa ada pernyataan yang tidak dapat dibuktikan. Tetapi, sebagai suatu peraturan, satu-satunya contoh pernyataan semacam itu adalah konstruksi Gödel sendiri (“Saya tidak dapat dibuktikan”). Teorema Goodstein adalah contoh yang bagus dari pernyataan seperti itu.

Terlebih lagi, ternyata tata cara dalam beberapa hal mengukur kekuatan teori . 'Kekuatan' aritmatika formal adalah $$$\ epsilon_0$ , teori himpunan Kripke-Plateka yang disederhanakan memiliki kekuatan ordinal Feferman-Schutte , dll.

Tourniquet Timah - Matematika - kompetisi bahasa C

Sebuah kompetisi diadakan untuk menghasilkan jumlah besar. Tidak, pemrograman untuk mesin Turing masih terlalu kejam, jadi C digunakan untuk beberapa mesin abstrak tak terbatas dengan sizeof (int) = infinity. Anda juga bisa menggunakan malloc (), dan jumlah memori, seperti stack, tidak terbatas. Hanya panjang program terbatas - program harus masuk dalam 512 byte (tidak termasuk spasi), tetapi penggunaan preprocessor (#define) diizinkan.

Hasilnya diterbitkan di situs web matematika . Pada saat yang sama memeriksa desain situs ahli matematika sungguhan. Hasilnya ada di sini . Ini adalah teks dari program, yang mengambil tempat kedua, memberikan nomor

$$

$$f_ {w ^ w} (10 ^ {500})$$

 typedef int J; JP(J x,J y) { return x+y ? x%2 + y%2*2 + P(x/2,y/2)*4 : 0 ;} JH(J z) { return z ? z%2 + 2*H(z/4) : 0 ;} JI(J f,J e,J r){ return f ? P(P(f,e),r) : r ;} JM(J x,J e) { return x ? I(x%2, M(e,0), M(x/2, e+1)) : 0 ;} JD(J,J); JE(J f,J e,J r,J b) { return e ? E(1, D(e,b), I(b-1, D(e,b), I(f-1,e,r)), b) : I(f-1,e,r) ; } JD(J x,J b) { return x ? E( H(H(x)), H(H(x)/2), H(x/2), b) : 0 ;} JF(J x,J b) { return x ? F(D(x,b+1),b+1) : b ;} JG(J x) { return F(M(x,9), 9) ;} J f(J n,J x) { return n ? f(n-1, G(x ? f(n,x-1) : n)) : G(x) ;} J g(J x) { return f(x,x) ;} J h(J n,J x) { return n ? h(n-1, g(x ? h(n,x-1) : n)) : g(x) ;} J main(void) { return h(g(9),9) ;} 

Teks program pemenang lebih panjang, saya hanya ingin menunjukkan dari mana ia dimulai:

 #define R { return #define PP ( #define LL ( #define TS (v, y, c, #define C ), #define X x) #define F );} 

Tetapi bahkan penyelenggara kontes merasa sulit untuk mengevaluasi seberapa besar angkanya (ditulis sangat besar )

Berang-berang yang sibuk

Oke, cukup untuk berurusan dengan angka kecil, mari kita lakukan yang besar. Bayangkan bahwa kontes universal telah diselenggarakan untuk menulis sebuah program untuk menghasilkan jumlah terbesar. Karena jumlah program tidak lebih dari 512 karakter, tentu saja, selalu ada pemenang absolut. Mari kita tunjuk sebagai BB (512) - fungsi berang-berang yang sibuk .

Jelas bahwa BB (1024) >> BB (512). Tetapi seberapa cepat fungsi BB tumbuh? Ternyata itu tumbuh lebih cepat dari semua yang kami temui. Fungsi BB itu sendiri secara algoritmik tidak dapat dipecahkan, tidak dapat dihitung pada komputer. Namun seiring dengan meningkatnya durasi program yang valid, kami dapat menerapkan semakin banyak gagasan baru. Jadi BB tumbuh lebih cepat dari pada fungsi yang dapat ditentukan secara algoritmik.

FOOT BESAR

Oke, cukup untuk berurusan dengan angka kecil, mari kita lakukan yang besar. Ah, sudahkah aku mengatakan itu? Akan lebih baik menjalankan BB (BB (n)). Tetapi karena BB tidak dapat dihitung, ada kesulitan teknis dengan ini (fungsi seperti itu dapat dihitung pada mesin Turing dengan oracle - tidak untuk membingungkan oracle dengan Oracle DBMS).

Tetapi Anda dapat melakukannya dengan lebih mudah, alih-alih suatu program, pertimbangkan rumus dengan penjumlahan panjang n. Rumus kuantifier tidak masalah jika sesuatu dapat dihitung atau tidak. Jadi Anda setidaknya dapat mengambil fungsi BB (1.000.000.000), dan menerapkannya pada diri Anda sendiri BB (BB (BB (1.000.000))) kali. Dan ini hanya apa yang pertama kali terlintas dalam pikiran.

Angka terbesar yang dapat dilambangkan dengan rumus paling banyak n karakter dilambangkan dengan FOOT (n).

$$

$$BIG FOOT = FOOT ^ {10} (10 ^ {100})$$

PS

Untuk artikel selanjutnya saya ingin memahami apa yang menjadi fokus, silakan ikut serta dalam survei ini