Mengurangi ukuran sampel data eksperimental tanpa kehilangan informasi

Apa masalah histogram data eksperimental

Dasar manajemen kualitas produk dari setiap perusahaan industri adalah pengumpulan data eksperimental dengan proses selanjutnya.

Pemrosesan awal hasil eksperimen melibatkan membandingkan hipotesis tentang hukum distribusi data, yang menggambarkan, dengan kesalahan terkecil, variabel acak atas sampel yang diamati.

Untuk ini, sampel disajikan dalam bentuk histogram yang terdiri dari $$$k$ kolom dibangun pada interval panjang $$$d$ .

Identifikasi bentuk distribusi hasil pengukuran juga memerlukan sejumlah masalah yang efisiensi solusinya berbeda untuk distribusi yang berbeda (misalnya, menggunakan metode kuadrat terkecil atau menghitung perkiraan entropi).

Selain itu, identifikasi distribusi juga diperlukan karena penghamburan semua perkiraan (standar deviasi, kelebihan, kelebihan, counterexcess, dll.) Juga tergantung pada bentuk undang-undang distribusi.

Keberhasilan mengidentifikasi bentuk distribusi data eksperimental tergantung pada ukuran sampel dan, jika kecil, fitur distribusi ditutupi oleh keacakan sampel itu sendiri. Dalam praktiknya, tidak mungkin untuk memberikan ukuran sampel yang besar, misalnya, lebih dari 1000, karena berbagai alasan.

Dalam situasi seperti itu, penting untuk mendistribusikan data sampel dengan cara terbaik dalam interval, ketika seri interval diperlukan untuk analisis dan perhitungan lebih lanjut.

Oleh karena itu, untuk identifikasi yang berhasil, perlu untuk memecahkan masalah menetapkan jumlah interval k

A. Hald dalam buku [1] secara luas meyakinkan bahwa ada jumlah interval pengelompokan yang optimal ketika amplop bertahap dari histogram yang dibangun pada interval-interval ini paling dekat dengan kurva distribusi yang halus dari populasi umum.

Salah satu tanda praktis mendekati optimal adalah hilangnya dip dalam histogram, dan k terbesar dianggap dekat dengan optimal, di mana histogram masih mempertahankan karakter yang halus.

Jelas, jenis histogram tergantung pada konstruksi interval milik variabel acak, namun, bahkan dalam kasus partisi yang seragam, metode konstruksi yang memuaskan masih belum tersedia.

Partisi, yang dapat dianggap benar, mengarah pada fakta bahwa kesalahan aproksimasi oleh fungsi konstan piecewise dari kepadatan distribusi yang seharusnya kontinu (histogram) akan minimal.

Kesulitan disebabkan oleh fakta bahwa estimasi kepadatan tidak diketahui, oleh karena itu, jumlah interval sangat mempengaruhi bentuk distribusi frekuensi sampel akhir.

Untuk panjang sampel tetap, pembesaran interval partisi tidak hanya mengarah pada penyempurnaan probabilitas empiris jatuh ke dalamnya, tetapi juga hilangnya informasi yang tak terhindarkan (baik dalam arti umum maupun dalam arti kurva distribusi kepadatan kepadatan), oleh karena itu, dengan pembesaran lebih lanjut yang tidak dapat dibenarkan, distribusi yang diteliti terlalu banyak diperhalus. .

Setelah itu muncul, tugas membagi secara optimal rentang di bawah histogram tidak hilang dari bidang pandang spesialis, dan sampai muncul satu-satunya pendapat tentang solusinya, tugas itu akan tetap relevan.

Pilihan kriteria untuk mengevaluasi kualitas histogram data eksperimen

Kriteria Pearson, seperti diketahui, mengharuskan membagi sampel ke dalam interval - di dalamnya perbedaan di antara model yang diadopsi dan sampel yang dibandingkan dievaluasi.

$$$\ chi ^ {2} = \ sum_ {j = 1} ^ {m} \ frac {(E_ {j} -M_ {j}) ^ {2}} {M_ {j}}$

dimana: $$$E_ {j}$ - Frekuensi eksperimental $$$(n_ {j})$ ; $$$M_ {j}$ - nilai frekuensi dalam kolom yang sama; m-jumlah kolom histogram.

Namun, penerapan kriteria ini dalam kasus interval panjang konstan, biasanya digunakan untuk membuat histogram, tidak efisien. Oleh karena itu, dalam pekerjaan pada efektivitas kriteria Pearson, interval dianggap tidak dengan panjang yang sama, tetapi dengan probabilitas yang sama sesuai dengan model yang diterima.

Namun, dalam kasus ini, jumlah interval dengan panjang yang sama dan jumlah interval dengan probabilitas yang sama berbeda beberapa kali (dengan pengecualian distribusi yang sama-sama berpeluang), yang memungkinkan seseorang meragukan keandalan hasil yang diperoleh dalam [2].

Sebagai kriteria kedekatan, disarankan untuk menggunakan koefisien entropi, yang dihitung sebagai berikut [3]:

$$$k_ {e} = \ frac {dn} {2 \ sigma} 10 ^ {\ beta}$

$$$\ beta = - \ frac {1} {n} \ sum_ {i = 1} ^ {m} {n_ {i} lg (n_ {i})}$

dimana: $$$n_ {i}$ - jumlah pengamatan dalam interval ke-i $$$i = 0, ..., m$

Algoritma untuk menilai kualitas histogram dari data eksperimen menggunakan koefisien entropi dan modul numpy.histogram

Sintaks untuk menggunakan modul adalah sebagai berikut [4]:

numpy.histogram (a, nampan = m, range = Tidak ada, normed = Tidak ada, bobot = Tidak ada, kepadatan = Tidak ada)

Kami akan mempertimbangkan metode untuk menemukan angka m optimal interval pemisahan histogram yang diterapkan dalam modul numpy.histogram:

• 'otomatis' - peringkat maksimum 'sturges' dan 'fd' , memberikan kinerja yang baik;
• 'fd' (Freedman Diaconis Estimator) - evaluator yang dapat dipercaya (tahan emisi) yang memperhitungkan variabilitas dan ukuran data;
• 'doane' - versi perbaikan dari perkiraan angka yang bekerja lebih akurat dengan kumpulan data dengan distribusi yang tidak normal;
• 'scott' adalah evaluator yang kurang andal yang memperhitungkan variabilitas dan ukuran data;
• 'batu' - evaluator didasarkan pada pemeriksaan silang dari perkiraan kuadrat kesalahan, dapat dianggap sebagai generalisasi aturan Scott;
• 'beras' - penilai tidak memperhitungkan variabilitas, tetapi hanya ukuran data, sering melebih-lebihkan jumlah interval yang diperlukan;
• 'sturges' - metode (secara default) yang hanya memperhitungkan ukuran data, hanya optimal untuk data Gaussian dan meremehkan jumlah interval untuk set data non-Gaussian yang besar;
• 'sqrt' adalah estimator akar kuadrat untuk ukuran data yang digunakan oleh Excel dan program lain untuk perhitungan jumlah interval yang cepat dan mudah.

Untuk memulai deskripsi algoritma, kami mengadaptasi modul numpy.histogram () untuk menghitung koefisien entropi dan kesalahan entropi:

from numpy import* def diagram(a,m,n): z=histogram(a, bins=m) if type(m) is str:#       m=len(z[0]) y=z[0] d=z[1][1]-z[1][0]#   h=0.5*d*n*10**(-sum([w*log10(w) for w in y if w!=0])/n)#  ke=h/std (a)#    (1). return ke,h 

Sekarang perhatikan tahapan utama dari algoritma:

1) Kami membentuk sampel kontrol (selanjutnya disebut sebagai "sampel besar") yang memenuhi persyaratan untuk kesalahan dalam memproses data eksperimental . Dari sampel besar, dengan menghapus semua anggota aneh, kami membentuk sampel yang lebih kecil (selanjutnya disebut sebagai "sampel kecil");

2) Untuk semua 'evaluator' otomatis ',' fd ',' doane ',' scott ',' stone ',' rice ',' sturges ',' sqrt 'kami menghitung koefisien entropi ke1 dan kesalahan h1 dari sampel besar dan koefisien entropi ke2 dan kesalahan h2 untuk sampel kecil, serta nilai absolut dari perbedaan - abs (ke1-ke2);

3) Mengontrol nilai numerik evaluator pada level setidaknya empat interval, kami memilih evaluator yang menyediakan nilai minimum dari perbedaan absolut - abs (ke1-ke2).

4) Untuk keputusan akhir tentang pilihan penilai, kami membangun satu histogram distribusi untuk sampel besar dan kecil dengan penilai memberikan nilai abs minimum (ke1-ke2), dan pada yang kedua dengan penilai memberikan nilai abs maksimum (ke1-ke2). Munculnya lompatan tambahan dalam sampel kecil dalam histogram kedua menegaskan pilihan yang benar dari evaluator di yang pertama.

Pertimbangkan karya algoritma yang diusulkan pada sampel data dari publikasi [2]. Data diperoleh dengan memilih secara acak 80 kosong dari 500 dengan pengukuran massa berikutnya. Benda kerja harus memiliki massa dalam batas berikut: $$$m = 17 _ {- 0,4} ^ {+ 0,6}$ kg Kami menentukan parameter histogram optimal menggunakan daftar berikut:


Kami mendapatkan:

Simpangan baku untuk sampel (n = 80): 0,24
Harapan matematika untuk sampel (n = 80): 17.158
Simpangan baku untuk sampel (n = 40): 0,202
Harapan matematika dari sampel (n = 40): 17.138
ke1 = 1.95, h1 = 0.467, ke2 = 1.917, h2 = 0.387, dke = 0.033, m = otomatis
ke1 = 1.918, h1 = 0.46, ke2 = 1.91, h2 = 0.386, dke = 0.008, m = fd
ke1 = 1.831, h1 = 0.439, ke2 = 1.917, h2 = 0.387, dke = 0.086, m = doane
ke1 = 1.918, h1 = 0.46, ke2 = 1.91, h2 = 0.386, dke = 0.008, m = scott
ke1 = 1.898, h1 = 0.455, ke2 = 1.934, h2 = 0.39, dke = 0.036, m = batu
ke1 = 1.831, h1 = 0.439, ke2 = 1.917, h2 = 0.387, dke = 0.086, m = beras
ke1 = 1.95, h1 = 0.467, ke2 = 1.917, h2 = 0.387, dke = 0.033, m = sturges
ke1 = 1.831, h1 = 0.439, ke2 = 1.917, h2 = 0.387, dke = 0.086, m = sqrt



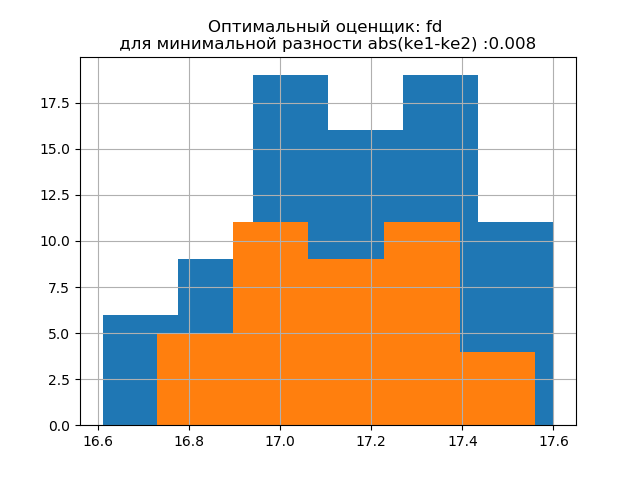
Bentuk distribusi sampel besar mirip dengan bentuk distribusi sampel kecil. Sebagai berikut dari skrip, 'fd' adalah evaluator yang dapat diandalkan (tahan emisi) yang memperhitungkan variabilitas dan ukuran data. Dalam hal ini, kesalahan entropi dari sampel kecil bahkan sedikit menurun: h1 = 0,46, h2 = 0,386 dengan sedikit penurunan koefisien entropi dari k1 = 1,918 ke k2 = 1,91.



Pola distribusi sampel besar dan kecil berbeda. Seperti yang dideskripsikan oleh deskripsi, 'doane' adalah versi perbaikan dari skor 'sturges' yang bekerja lebih baik dengan kumpulan data dengan distribusi yang tidak normal. Dalam kedua sampel, koefisien entropi mendekati dua, dan distribusinya mendekati normal. Penampilan lompatan tambahan dalam sampel kecil pada histogram ini, dibandingkan dengan yang sebelumnya, juga menunjukkan pilihan yang tepat dari evaluator 'fd' .

Kami menghasilkan dua sampel baru untuk distribusi normal dengan parameter mu = 20, sigma = 0,5 dan ukuran = 100 menggunakan relasi:

 a= list([round(random.normal(20,0.5),3) for x in arange(0,100,1)]) 

Metode yang dikembangkan berlaku untuk sampel yang diperoleh menggunakan program berikut:



Kami mendapatkan:
Simpangan baku untuk sampel (n = 100): 0,524
Harapan matematika untuk sampel (n = 100): 19,992
Simpangan baku untuk sampel (n = 50): 0,462
Harapan matematika dari sampel (n = 50): 20,002
ke1 = 1.979, h1 = 1.037, ke2 = 2.004, h2 = 0.926, dke = 0.025, m = otomatis
ke1 = 1.979, h1 = 1.037, ke2 = 1.915, h2 = 0.885, dke = 0.064, m = fd
ke1 = 1.979, h1 = 1.037, ke2 = 1.804, h2 = 0.834, dke = 0.175, m = doane
ke1 = 1.943, h1 = 1.018, ke2 = 1.934, h2 = 0.894, dke = 0.009, m = scott
ke1 = 1.943, h1 = 1.018, ke2 = 1.804, h2 = 0.834, dke = 0.139, m = batu
ke1 = 1.946, h1 = 1.02, ke2 = 1.804, h2 = 0.834, dke = 0.142, m = beras
ke1 = 1.979, h1 = 1.037, ke2 = 2.004, h2 = 0.926, dke = 0.025, m = sturges
ke1 = 1.946, h1 = 1.02, ke2 = 1.804, h2 = 0.834, dke = 0.142, m = sqrt



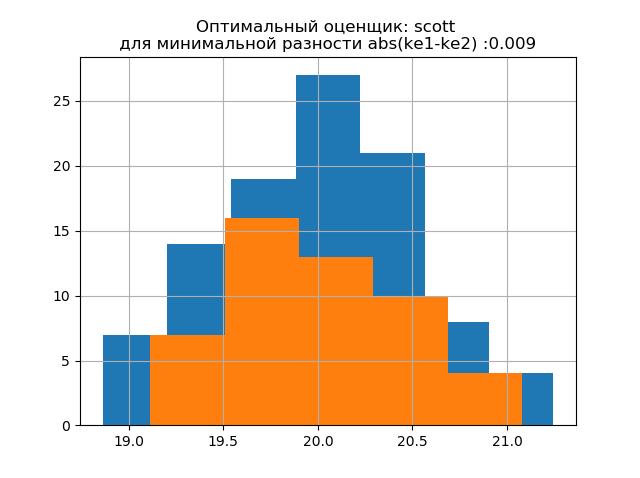
Bentuk distribusi sampel besar mirip dengan bentuk distribusi sampel kecil. Sebagai berikut dari uraian, 'scott' adalah evaluator yang kurang andal yang memperhitungkan variabilitas dan ukuran data. Dalam hal ini, kesalahan entropi dari sampel kecil bahkan sedikit menurun: h1 = 1,018 dan h2 = 0,894 dengan sedikit penurunan koefisien entropi dari k1 = 1,943 ke k2 = 1,934. . Perlu dicatat bahwa untuk sampel baru kami memiliki kecenderungan yang sama untuk mengubah parameter seperti pada contoh sebelumnya.



Pola distribusi sampel besar dan kecil berbeda. Sebagai berikut dari deskripsi, 'doane' adalah versi perbaikan dari perkiraan 'sturges' , yang bekerja lebih akurat dengan kumpulan data dengan distribusi yang tidak normal. Dalam kedua sampel, distribusi normal. Munculnya lompatan tambahan dalam sampel kecil pada histogram ini dibandingkan dengan yang sebelumnya juga menunjukkan pilihan yang benar dari evaluator 'scott' .

Penggunaan anti-aliasing untuk analisis komparatif histogram

Menghaluskan histogram yang dibangun di atas sampel besar dan kecil memungkinkan Anda untuk lebih akurat menentukan identitas mereka dari sudut pandang menjaga informasi yang terkandung dalam sampel yang lebih besar. Bayangkan dua histogram terakhir sebagai fungsi pemulusan:




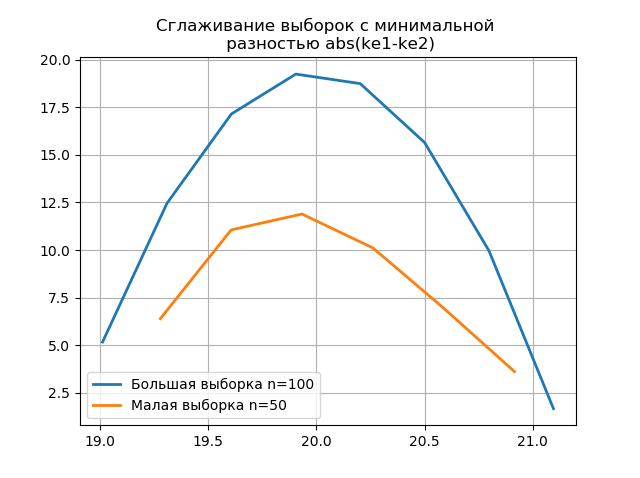
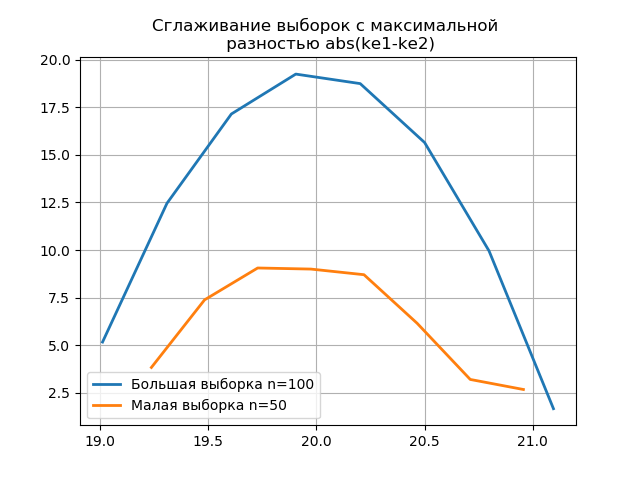
Penampilan lompatan tambahan dalam sampel kecil pada grafik histogram yang dihaluskan dibandingkan dengan yang sebelumnya juga menunjukkan pilihan yang benar dari penilai scott .

Kesimpulan

Perhitungan yang disajikan dalam artikel dalam kisaran sampel kecil yang umum dalam produksi mengkonfirmasi efisiensi menggunakan koefisien entropi sebagai kriteria untuk mempertahankan konten informasi sampel sambil mengurangi volumenya . Teknik menggunakan modul numpy.histogram versi terbaru dengan evaluator bawaan dianggap - 'otomatis', 'fd', 'doane', 'scott', 'scott', 'stone', 'rice', 'sturges', 'sqrt', yang cukup untuk optimasi analisis data eksperimen pada perkiraan interval.

Referensi:

1. Hald A. Statistik matematika dengan aplikasi teknis. - Moskow: Rumah Penerbitan. lit., 1956
2. Kalmykov V.V., Antonyuk F.I., Zenkin N.V.
Penentuan jumlah optimal kelas pengelompokan data eksperimen untuk perkiraan interval // Buletin Siberia Ilmiah Selatan - 2014. - No. 3. - P. 56-58.
3. Novitsky P. V. Konsep nilai entropi kesalahan // Teknik pengukuran - 1966. - No. 7. —S. 11-14.
4.numpy.histogram - NumPy v1.16 Manual