Geekly articles weekly

Monads dari sudut pandang programmer (dan sedikit teori kategori)

Pendahuluan


Bagaimana mengetahui bahwa seseorang memahami apa itu monad? Dia sendiri akan memberi tahu Anda tentang ini dalam 5 menit pertama komunikasi dan pasti akan mencoba menjelaskannya. Dia juga akan menulis teks tentang itu dan, jika mungkin, mempublikasikannya di suatu tempat, sehingga semua orang juga mengerti apa itu monad.


Di antara programmer fungsional, terutama pada Haskell, monad telah menjadi sedikit meme lokal. Mereka sering mencoba menjelaskan, mulai dari kasus khusus dan langsung memberi contoh penggunaan. Karena itu, pendengar mungkin tidak memahami esensi utama konsep, dan monad akan tetap menjadi ilmu hitam, atau hanya sebagai alat untuk menghancurkan efek samping dalam bahasa murni fungsional.


Pertama saya akan berbicara tentang konsep dasar teori kategori, dan kemudian dari sudut pandang praktis kita akan mendekati definisi monad dan melihat bahwa pada kenyataannya, sangat banyak programmer menggunakan abstraksi yang kuat ini dalam salah satu manifestasinya.


Presentasi saya sebagian besar didasarkan pada buku Bartosz Milewski, Kategori Teori untuk Programmer, yang dibuat sebagai serangkaian posting blog , tersedia dalam PDF , dan baru-baru ini diterbitkan dalam bentuk kertas.


Contoh diberikan dalam Haskell, diasumsikan bahwa pembaca sudah terbiasa dengan sintaks dan konsep dasar bahasa. Dalam buku yang disebutkan ada contoh dalam C ++, Anda dapat membandingkan kemurnian dan kelengkapan kode.



Kategori


Definisi


Kategori itu sendiri adalah konstruksi yang sangat sederhana. Kategori adalah kumpulan benda dan morfisme di antara mereka. Morfisme dapat dianggap sebagai panah searah yang menghubungkan objek. Dalam kasus umum, tidak ada yang diketahui tentang esensi dari objek itu sendiri. Teori kategori tidak bekerja dengan objek, tetapi dengan morfisme, atau lebih tepatnya, dengan komposisinya .


Notasi berikut digunakan:


  • Ob C - objek dari kategori C ;
  • Hom C (A, B) - morfisme dari A ke B;
  • g ∘ f adalah komposisi morfisme f dan g.

Dalam mendefinisikan suatu kategori, morfisme tunduk pada batasan tambahan:


  1. Untuk sepasang morfisme f dan g, jika f adalah morfisme dari A ke B (f ∈ Hom (A, B)), g adalah morfisme dari B ke C (g ∈ Hom (B, C)), maka terdapat komposisi g ∘ f adalah morfisme dari A ke C (g ∘ f ∈ Hom (A, C)).
  2. Untuk setiap objek, id morfisme identitas A ∈ Hom (A, A) diberikan.

Ada dua sifat penting yang harus dipenuhi oleh suatu kategori (aksioma teori kategori):


  1. Asosiativitas komposisi: h ∘ (g ∘ f) = (h ∘ g) ∘ f;
  2. Komposisi dengan morfisme identitas: jika f ∈ Hom (A, B), maka f ∘ id A = id B ∘ f = f.

Kategori sangat mudah dan secara alami divisualisasikan sebagai grafik berarah. Pada prinsipnya, setiap grafik yang berorientasi dapat diperluas ke kategori dengan menambahkan komposisi morfisme dan morfisme yang identik, jika perlu.



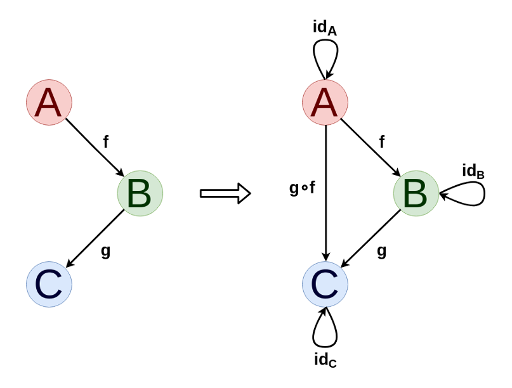
Untuk kategori apa pun, Anda dapat mendefinisikan kategori ganda (dilambangkan dengan C op , di mana morfisme diperoleh dengan memutar panah dari kategori asli, dan objek-objeknya sama. Ini memungkinkan kita untuk merumuskan pernyataan ganda dan teorema, yang kebenarannya tidak berubah ketika panah itu terbalik.


Objek dan morfisme tidak harus membentuk himpunan (dalam pengertian klasik, dari himpunan teori), oleh karena itu, dalam kasus umum, frasa "kelas objek" digunakan. Kategori di mana kelas objek dan morfisme masih ditetapkan disebut kategori kecil . Selanjutnya kami hanya akan bekerja dengan mereka.


Jenis dan Fungsi


, Haskell, — . , Int Bool — , Int -> Bool — .


id, :


id :: a -> a
id x = x

— , Haskell :


f :: a -> b
g :: b -> c
g . f :: a -> c
(g . f) x = g (f x)

, , — , Set. , — , : . bottom, _|_. , , , bottom. Haskell, , Hask. , Set. , , : HomC(A, B) ∈ C. , a -> b — Haskell.


.


Void, ( ). absurd, , , Void, :


absurd :: Void -> a

Unit, — , (). unit , :


unit :: a -> Unit
unit _ = ()

— Bool:


data Bool = True | False

, Void, Unit Bool.


Void , absurd, Bool, Unit. , Void, , .


Bool -> Unit , unit, . Unit -> Bool . (), True, False. , Unit Bool:


true, false :: a -> Bool
true _ = True
false _ = False

Bool Bool — , 4 ( n — 22n): id, true false, , not:


not :: Bool -> Bool
not True = False
not False = True

, :



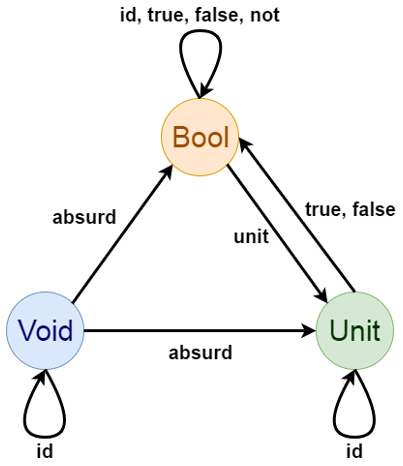
Haskell- .



— . , C D, F . -, C D. a — C, F a — D, . -, : f :: a -> b C F f :: F a -> F b D.



, " " :


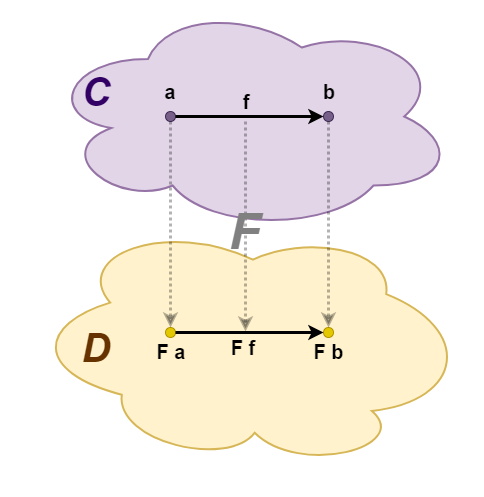
  1. h = g ∘ f, F h = F g ∘ F f.
  2. ida — a, F ida = idF a — F a.

, "" : , , . , , () . , .


. , F :: C -> D G :: D -> E G . F :: C -> E. , , , , . IdC, IdD IdE. , , .



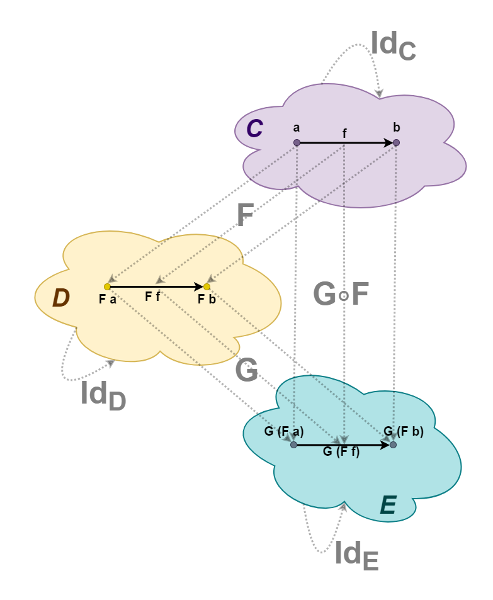
, , -, — (). , Cat ( ).


Haskell . , , - , .


Maybe , a Maybe a ( Maybe !):


data Maybe a = Nothing | Just a

, f :: a -> b F f :: Maybe a -> Maybe b. fmap. , ( ):


--          f                F f
--      /------\    /------------------\
fmap :: (a -> b) -> (Maybe a -> Maybe b)
fmap _ Nothing = Nothing
fmap f (Just x) = Just (f x)

, Maybe — . , , Functor. fmap, , ( — ):


class Functor f where
  fmap :: (a -> b) -> f a -> f b

— , , fmap . f a -> f b, , .



, , , .. , . : , - .


. , . , , — Haskell.


: upCase, , toWords, . toUpper words:


upCase :: String -> String
upCase = map toUpper

toWords :: String -> [String]
toWords = words

:


processString :: String -> [String]
processString = toWords . upCase

, . , processString "upCase toWords".


— , . -, , , -, , .


, a , .


newtype Writer a = Writer (a, String)

, Writer — , fmap:


instance Functor Writer where
  fmap f (Writer (x, s)) = Writer (f x, s)

upCase toWords , , "" Writer:


upCase :: String -> Writer String
upCase s = Writer (map toUpper s, "upCase ")

toWords :: String -> Writer [String]
toWords s = Writer (words s, "toWords ")

, , - . , b , , c c , :


compose :: (a -> Writer b) -> (b -> Writer c) -> (a -> Writer c)
compose f g = \x -> let Writer (y, s1) = f x
                        Writer (z, s2) = g y
                    in Writer (z, s1 ++ s2)

processString :


processString :: String -> [String]
processString = compose upCase toWords

. () a -> b a -> Writer b , a b. , .. a -> Writer a:


writerId :: a -> Writer a
writerId x = Writer (x, "")

, , Hask. , a b a -> b, a -> m b, .. "" - m. (embellished). m, Writer — .


C m. K, , C, .. ObK = ObC. a -> b K a -> m b C: HomK(a, b) = HomC(a, m b). , , K — C.


, , , . , m — . Haskell ( Hask):


class Monad m where
  --    
  (>=>)  :: (a -> m b) -> (b -> m c) -> (a -> m c)
  --  
  return :: a -> m a

>=>, "fish", : . , , — , , , . Writer — , compose — >=>, writerId — return.


>=> . , -. a, f, , , bind:


f >=> g = \a -> let mb = f a
                in (bind mb g)
  where
    bind :: m b -> (b -> m c) -> m c

bind b " " m , b m c. >=>. : m b -> (b -> m c) -> m c. , . "" Haskell >>=, bind, return:


class Monad m where
  (>>=)  :: m a -> (a -> m b) -> m b
  return :: a -> m a

, - b -> m c b, m b. , m, fmap, (a -> m b) -> m a -> m (m b). >>= m (m b) m b, "" , . join:


ma >>= g = join (fmap g ma)
  where
    join :: m (m a) -> m a

, Writer :


join :: Writer (Writer a) -> Writer a
join (Writer ((Writer (x, s2)), s1)) = Writer (x, s1 ++ s2)

Monad:


class Functor m => Monad m where
  join   :: m (m a) -> m a
  return :: a -> m a

, m . , fmap >>=:


fmap :: (a -> b) -> m a -> m b
fmap f ma = ma >>= (\a -> return (f a))


, "" .



(.. , ) .


(a -> [b]) -> (b -> [c]) -> (a -> [c]). :


(>=>) :: (a -> [b]) -> (b -> [c]) -> (a -> [c])
f >=> g = \x -> concat (map g (f x))

. a, , — f [b]. , b — g : map g (f x) :: [[c]]. , .


>>= :


(>>=) :: [a] -> (a -> [b]) -> [b]
xs >>= f = concat (map f xs)

return :: a -> [a]. :


return :: a -> [a]
return x = [x]

Monad:


instance Monad [] where
  xs >>= f = concat (map f xs)
  return x = [x]

, . , , . , — , ..



, , - .


, , Maybe. Just, — Nothing. , , :


(>=>) :: (a -> Maybe b) -> (b -> Maybe c) -> (a -> Maybe c)
f >=> g = \x -> case f x of
                  Just y  -> g y
                  Nothing -> Nothing

Monad Maybe:


instance Monad Maybe where
  (Just x) >>= f = f x
  Nothing  >>= f = Nothing
  return x = Just x

, . , - , , - . Either String a, : , . :


data Either a b = Left a | Right b

, . . :


type WithException a = Either String a

Maybe:


(>=>) :: (a -> WithException b) -> (b -> WithException c) -> (a -> WithException c)
f >=> g = \x -> case f x of
                  Right y -> g y
                  err     -> err

Monad :


instance Monad WithException where
  (Right x) >>= f = f x
  err >>= f = err
  return x = Right x


, , write-only , . a -> b , , . , , ( , ):


a -> s -> (b, s)

:


newtype State s a = State (s -> (a, s))

s , State s . runState:


runState :: State s a -> s -> (a, s)
runState (State f) s = f s

Functor:


instance Functor (State s) where
  fmap f state = State st'
    where
     st' prevState = let (a, newState) = runState state prevState
                     in (f a, newState)

, a b, , a -> State s b, State s — . , :


(>=>) :: (a -> State s b) -> (b -> State s c) -> (a -> State s c)
f >=> g = \x -> State (\s -> let (y, s') = runState (f x) s
                             in runState (g y) s')

Monad. , return, , -:


instance Monad (State s) where
  stateA >>= f = State (\s -> let (a, s') = runState stateA s
                              in runState (f a) s')
  return a = State (\s -> (a, s))

, . , Unit s , Unit -> State s s:


get :: Unit -> State s s
get _ = State (\s -> (s, s))

, Unit . , .


, , . , , , s Unit, s -> State s Unit:


put :: s -> State s Unit
put s = State (\_ -> ((), s))

, , /. , " " RealWorld, . RealWorld - , (, ). :


type IO a = State RealWorld a

IO — , Haskell, "". , . , , , -, .

Source: https://habr.com/ru/post/id445488/

More articles:


All Articles