💪 🐨 🙅🏾 Neural Quantum States - Representasi fungsi gelombang oleh jaringan saraf 🥨 🙎🏽 👏

Dalam artikel ini, kami akan mempertimbangkan aplikasi yang tidak biasa dari jaringan saraf pada umumnya dan mesin Boltzmann terbatas khususnya untuk memecahkan dua masalah kompleks mekanika kuantum - menemukan energi keadaan dasar dan mendekati fungsi gelombang dari sistem banyak-tubuh.

Kita dapat mengatakan bahwa ini adalah pengisahan ulang yang bebas dan disederhanakan dari sebuah artikel [2], diterbitkan dalam Science pada 2017 dan beberapa karya selanjutnya. Saya tidak menemukan eksposisi ilmiah populer dari karya ini dalam bahasa Rusia (dan hanya versi bahasa Inggris ini), meskipun bagi saya itu tampak sangat menarik.

Konsep esensial minimum dari mekanika kuantum dan pembelajaran dalam

Saya ingin segera mencatat bahwa definisi ini sangat disederhanakan . Saya membawa mereka untuk mereka yang masalah yang dijelaskan adalah hutan gelap.

Suatu negara hanyalah seperangkat jumlah fisik yang menggambarkan suatu sistem. Sebagai contoh, untuk elektron yang terbang di ruang angkasa itu akan menjadi koordinat dan momentumnya, dan untuk kisi kristal itu akan menjadi seperangkat putaran atom yang terletak di node-nya.

Fungsi gelombang dari sistem adalah fungsi kompleks dari keadaan sistem. Kotak hitam tertentu yang mengambil input, misalnya, satu set putaran, tetapi mengembalikan bilangan kompleks. Properti utama fungsi gelombang yang penting bagi kami adalah kuadratnya sama dengan probabilitas kondisi ini:

P s i (s) P s i (s)^{*} = P (s)

$\ Psi (s) \ Psi (s) ^ * = P (s)$

Adalah logis bahwa kuadrat dari fungsi gelombang harus dinormalisasi menjadi satu (dan ini juga merupakan salah satu masalah yang signifikan).

Ruang Hilbert - dalam kasus kami, definisi seperti itu sudah cukup - ruang dari semua kemungkinan status sistem. Misalnya, untuk sistem 40 putaran yang dapat mengambil nilai +1 atau -1, ruang Hilbert adalah segalanya

2^{40}

$2 ^ {40}$ kondisi yang memungkinkan. Untuk koordinat yang dapat mengambil nilai

[- i n f t y, + i n f t y]

$[- \ infty, + \ infty]$ , dimensi ruang Hilbert tidak terbatas. Ini adalah dimensi luar biasa dari ruang Hilbert untuk setiap sistem nyata yang merupakan masalah utama yang tidak memungkinkan penyelesaian persamaan secara analitis: dalam proses tersebut akan ada integral / penjumlahan atas seluruh ruang Hilbert yang tidak dapat dihitung “langsung”. Fakta yang aneh: untuk seluruh kehidupan Semesta Anda hanya dapat bertemu sebagian kecil dari semua keadaan yang mungkin termasuk dalam ruang Hilbert. Ini diilustrasikan dengan sangat baik oleh gambar dari artikel tentang Tensor Networks [1], yang secara skematis menggambarkan seluruh ruang Hilbert dan negara-negara yang dapat dipenuhi setelah polinomial dari karakteristik kompleksitas ruang (jumlah benda, partikel, putaran, dll.)

Mesin Boltzmann terbatas - jika sulit untuk dijelaskan, ini adalah model probabilistik grafis yang tidak diarahkan, yang batasannya adalah independensi kondisional dari kemungkinan node satu lapisan dari node lapisan yang sama. Jika dengan cara sederhana, maka ini adalah jaringan saraf dengan input dan satu lapisan tersembunyi. Nilai output neuron dalam lapisan tersembunyi dapat 0 atau 1. Perbedaan dari jaringan saraf biasa adalah bahwa output dari neuron lapisan tersembunyi adalah variabel acak yang dipilih dengan probabilitas yang sama dengan nilai fungsi aktivasi:

P_{i} (1) = s i g m a (b_{i} + s u m_{j} W_{i j} s_{j})

$P_i (1) = \ sigma (b_i + \ sum_jW_ {ij} s_j)$

dimana

s i g m a

$\ sigma$ - fungsi aktivasi sigmoid ,

b_{i}

$b_i$ - Mengimbangi untuk neuron ke-i,

W

$W$ - berat jaringan saraf,

s_{j}

$s_j$ - Lapisan yang terlihat. Mesin Boltzmann terbatas termasuk dalam apa yang disebut "model energi", karena kita dapat menyatakan probabilitas keadaan tertentu dari mesin yang menggunakan energi mesin ini:

E (v, h) = - a^{T} v - b^{T} h - v^{T} W h

$E (v, h) = -a ^ Tv - b ^ Th - v ^ TWh$

di mana v dan h adalah lapisan yang terlihat dan tersembunyi, a dan b adalah perpindahan dari lapisan yang terlihat dan tersembunyi, W adalah bobot. Maka probabilitas negara direpresentasikan dalam bentuk:

P (v, h) = f r a c 1 Z e^{- E (v, h)}

$P (v, h) = \ frac {1} {Z} e ^ {- E (v, h)}$

di mana Z adalah istilah normalisasi, juga disebut jumlah statistik (perlu sehingga probabilitas total sama dengan kesatuan).

Pendahuluan

Saat ini, ada pendapat di antara para spesialis dalam pembelajaran mendalam yang terbatas
Mesin Boltzmann (selanjutnya - OMB) adalah konsep usang yang praktis tidak berlaku dalam tugas nyata. Namun, pada 2017, sebuah artikel [2] muncul di Science yang menunjukkan penggunaan OMB yang sangat efisien untuk masalah mekanika kuantum.

Para penulis memperhatikan dua fakta penting yang mungkin tampak jelas, tetapi mereka tidak pernah terpikir oleh siapa pun sebelumnya:

OMB adalah jaringan saraf yang, menurut teorema universal Tsybenko , secara teoritis dapat memperkirakan fungsi apa pun dengan akurasi tinggi yang sewenang-wenang (masih ada banyak batasan, tetapi Anda dapat mengabaikannya).
OMB adalah sistem yang probabilitas masing-masing negara bagian adalah fungsi dari input (lapisan yang terlihat), bobot dan perpindahan dari jaringan saraf.

Baik dan selanjutnya penulis mengatakan: biarkan sistem kami sepenuhnya dijelaskan oleh fungsi gelombang, yang merupakan akar dari energi OMB, dan input OMB adalah karakteristik kondisi sistem kami (koordinat, putaran, dll.):

P s i = f r a c 1 Z s q r t e^{E (s, h)}

$\ Psi = \ frac {1} {Z} \ sqrt {e ^ {E (s, h)}}$

di mana s adalah karakteristik negara (misalnya, punggung), h adalah output dari lapisan tersembunyi OMB, E adalah energi OMB, Z adalah konstanta normalisasi (jumlah statistik).

Itu saja, artikel dalam Sains sudah siap, maka hanya beberapa detail kecil yang tersisa. Sebagai contoh, perlu untuk memecahkan masalah fungsi partisi yang tidak dapat dihitung karena ukuran ruang Hilbert yang sangat besar. Dan teorema Tsybenko memberi tahu kita bahwa jaringan saraf dapat memperkirakan fungsi apa pun, tetapi teorinya tidak mengatakan bagaimana menemukan set bobot dan offset jaringan yang cocok untuk ini. Yah, dan seperti biasa, kesenangan dimulai di sini.

Pelatihan model

Sekarang ada beberapa modifikasi dari pendekatan asli, tetapi saya hanya akan mempertimbangkan pendekatan dari artikel asli [2].

Tantangan

Dalam kasus kami, tugas pelatihan adalah sebagai berikut: untuk menemukan perkiraan fungsi gelombang yang akan membuat keadaan dengan energi minimum paling mungkin. Ini secara intuitif jelas: fungsi gelombang memberi kita kemungkinan suatu keadaan, nilai eigen dari Hamiltonian (operator energi, atau bahkan lebih sederhana, energi - dalam kerangka artikel ini, pengertian ini cukup) untuk fungsi gelombang adalah energi. Semuanya sederhana.

Pada kenyataannya, kami akan berusaha untuk mengoptimalkan kuantitas lain, yang disebut energi lokal, yang selalu lebih besar atau sama dengan energi keadaan dasar:

E_{l o c} (s i g m a) = R e s u m_{s i g m a s i g m a^{'}} H_{s i g m a s i g m a^{'}} f r a c P s i (s i g m a^{'}) P s i (s i g m a)

$E_ {loc} (\ sigma) = Re \ sum _ {\ sigma \ sigma '} H _ {\ sigma \ sigma'} \ frac {\ Psi (\ sigma ')} {\ Psi (\ sigma)}$

disini

s i g m a

$\ sigma$ Apakah kondisi kita

s i g m a^{'}

$\ sigma '$ - semua kemungkinan status ruang Hilbert (pada kenyataannya kami akan mempertimbangkan nilai yang lebih mendekati),

H_{s i g m a s i g m a^{'}}

$H _ {\ sigma \ sigma '}$ Merupakan elemen matriks dari Hamiltonian. Sangat tergantung pada Hamiltonian spesifik, misalnya, untuk model Ising, ini adil

f (s i g m a)

$f (\ sigma)$ jika

s i g m a = s i g m a^{'}

$\ sigma = \ sigma '$ , dan

- h a m p i r

$-hampir$ dalam semua kasus lainnya. Jangan berhenti di sini sekarang; penting bahwa elemen-elemen ini dapat ditemukan untuk berbagai warga Hamilton yang populer.

Proses optimasi

Sampling

Bagian penting dari pendekatan dari artikel asli adalah proses pengambilan sampel. Variasi yang dimodifikasi dari algoritma Metropolis-Hastings digunakan. Intinya adalah:

Kami mulai dari keadaan acak.
Kami mengubah tanda putaran yang dipilih secara acak ke sebaliknya (untuk koordinat ada modifikasi lain, tetapi mereka juga ada).
Dengan probabilitas sama dengan $P (\ sigma '| \ sigma) = \ Besar | {\ frac {\ Psi (\ sigma')} {\ Psi (\ sigma)} \ Besar | ^ 2$ , pindah ke negara baru.
Ulangi N kali.

Akibatnya, kami memperoleh satu set keadaan acak yang dipilih sesuai dengan distribusi yang diberikan fungsi gelombang kami. Anda dapat menghitung nilai energi di setiap negara bagian dan ekspektasi matematis energi

m a t h b b E (E_{l o c})

$\ mathbb {E} (E_ {loc})$ .

Dapat ditunjukkan bahwa estimasi gradien energi (lebih tepatnya, nilai yang diharapkan dari Hamiltonian) sama dengan:

G_{k} (x) = 2 * (E_{l o c} (x) - m a t h b b E (E_{l o c})) * D_{k}^{*} (x)

$G_k (x) = 2 * (E_ {loc} (x) - \ mathbb {E} (E_ {loc})) * D ^ * _ k (x)$

Kesimpulan

Ini dari kuliah yang diberikan oleh G. Carleo pada tahun 2017 untuk Advanced School on Quantum Science dan Quantum Technology. Ada entri di Youtube.

Nyatakan:

D_{k}^{*} (x) = f r a c p a r t i a l_{p_{k}} P s i (x) P s i (x)

$D ^ * _ k (x) = \ frac {\ partial_ {p_k} \ Psi (x)} {\ Psi (x)}$

Lalu:

p a r t i a l_{p_{k}} m a t h b b E (H) =

$\ partial_ {p_k} \ mathbb {E} (H) =$

p a r t i a l f r a c s u m_{x x^{'}} P s i^{*} (x) H_{x x^{'}} P s i (x^{'}) s u m_{x} | P s i (x) |^{2} =

$\ partial \ frac {\ sum_ {xx '} \ Psi ^ * (x) H_ {xx'} \ Psi (x ')} {\ sum_x | \ Psi (x) | ^ 2} =$

f r a c s u m_{x x^{'}} P s i^{*} (x) H_{x x^{'}} D_{k} (x^{'}) P s i (x^{'}) s u m_{x} | P s i (x) |^{2} + f r a c s u m_{x x^{'}} P s i^{*} (x) D_{k}^{*} (x) H_{x x^{'}} P s i (x^{'}) s u m_{x} | P s i (x) |^{2} -

$\ frac {\ sum_ {xx '} \ Psi ^ * (x) H_ {xx'} D_k (x ') \ Psi (x')} {\ sum_x | \ Psi (x) | ^ 2} + \ frac {\ sum_ {xx '} \ Psi ^ * (x) D_k ^ * (x) H_ {xx'} \ Psi (x ')} {\ sum_x | \ Psi (x) | ^ 2} -$

f r a c s u m_{x x^{'}} P s i^{*} (x) H_{x x^{'}} P s i (x^{'}) s u m_{x} | P s i (x) |^{2} f r a c s u m_{x} | P s i (x) |^{2} (D_{k} (x) - D_{k}^{*} (x)) s u m_{x} | P s i (x) |^{2} =

$\ frac {\ sum_ {xx '} \ Psi ^ * (x) H_ {xx'} \ Psi (x ')} {\ sum_x | \ Psi (x) | ^ 2} \ frac {\ sum_x | \ Psi (x) | ^ 2 (D_k (x) - D ^ * _ k (x))} {\ sum_x | \ Psi (x) | ^ 2} =$

f r a c s u m_{x x^{'}} f r a c P s i^{*} (x) P s i^{*} (x^{'}) H_{x x^{'}} D_{k} (x^{'}) | P s i (x^{'}) |^{2} + s u m_{x x^{'}} | P s i (x) |^{2} H_{x x^{'}} D_{k}^{*} (x^{'}) f r a c P s i (x^{'}) P s i (x) s u m_{x} | P s i (x) |^{2} -

$\ frac {\ sum_ {xx '} \ frac {\ Psi ^ * (x)} {\ Psi ^ * (x')} H_ {xx '} D_k (x') | \ Psi (x ') | ^ 2 + \ sum_ {xx '} | \ Psi (x) | ^ 2H_ {xx'} D ^ * _ k (x ') \ frac {\ Psi (x')} {\ Psi (x)}} {\ sum_x | \ Psi (x) | ^ 2} -$

m a t h b b E (H) f r a c s u m_{x} | P s i (x) |^{2} (D_{k} (x) + D_{k}^{*} (x)) s u m_{x} | P s i (x) |^{2} s e k i t a r

$\ mathbb {E} (H) \ frac {\ sum_x | \ Psi (x) | ^ 2 (D_k (x) + D ^ * _ k (x))} {\ sum_x | \ Psi (x) | ^ 2 } \ sekitar$

m a t h b b E (E_{l o c} D_{k}^{*}) - m a t h b b E (E_{l o c}) m a t h b b E (D_{k}^{*}) + C

$\ mathbb {E} (E_ {loc} D ^ * _ k) - \ mathbb {E} (E_ {loc}) \ mathbb {E} (D ^ * _ k) + C$

Maka kami baru saja menyelesaikan masalah optimasi:

Kami sampel negara dari OMB kami.
Kami menghitung energi setiap negara.
Perkirakan gradien.
Kami memperbarui bobot OMB.

Akibatnya, gradien energi cenderung nol, nilai energi menurun, seperti halnya jumlah negara baru yang unik dalam proses Metropolis-Hastings, karena dengan mengambil sampel dari fungsi gelombang yang sebenarnya kita hampir selalu mendapatkan keadaan dasar. Secara intuitif, ini tampak logis.

Dalam karya aslinya, untuk sistem kecil, nilai-nilai energi keadaan dasar diperoleh, sangat dekat dengan nilai-nilai pasti yang diperoleh secara analitis. Perbandingan dibuat dengan pendekatan terkenal untuk menemukan energi keadaan dasar, dan NQS menang, terutama mengingat kompleksitas komputasional NQS yang relatif rendah dibandingkan dengan metode yang dikenal.

NetKet - perpustakaan dari pendekatan "penemu"

Salah satu penulis artikel asli [2] bersama timnya mengembangkan pustaka NetKet yang sangat baik [3], yang berisi kernel-C yang sangat dioptimalkan dengan baik (menurut saya), serta API Python, yang bekerja dengan abstraksi tingkat tinggi.

Perpustakaan dapat diinstal melalui pip. Pengguna Windows 10 harus menggunakan Linux Subsystem untuk Windows.

Mari kita pertimbangkan bekerja dengan perpustakaan sebagai contoh rantai 40 putaran mengambil nilai + -1 / 2. Kami akan mempertimbangkan model Heisenberg, yang memperhitungkan interaksi tetangga.

NetKet memiliki dokumentasi yang sangat baik yang memungkinkan Anda dengan cepat mengetahui apa dan bagaimana melakukannya. Ada banyak model bawaan (punggung, boson, Ising, model Heisenberg, dll.), Dan kemampuan untuk sepenuhnya menggambarkan model itu sendiri.

Deskripsi Hitungan

Semua model disajikan dalam grafik. Untuk rantai kami, model Hypercube bawaan dengan satu dimensi dan kondisi batas periodik cocok:

import netket as nk graph = nk.graph.Hypercube(length=40, n_dim=1, pbc=True)

Deskripsi Ruang Hilbert

Ruang Hilbert kami sangat sederhana - semua putaran dapat mengambil nilai +1/2 atau -1/2. Untuk kasus ini, model bawaan untuk putaran cocok:

 hilbert = nk.hilbert.Spin(graph=graph, s=0.5)

Deskripsi Hamiltonian

Seperti yang sudah saya tulis, dalam kasus kami Hamiltonian adalah Heisenberg Hamiltonian yang memiliki operator bawaan:

 hamiltonian = nk.operator.Heisenberg(hilbert=hilbert)

Deskripsi RBM

Di NetKet, Anda dapat menggunakan implementasi RBM yang sudah jadi untuk spin - ini hanya kasus kami. Tetapi secara umum ada banyak mobil, Anda dapat mencoba yang berbeda.

 nk.machine.RbmSpin(hilbert=hilbert, alpha=4) machine.init_random_parameters(seed=42, sigma=0.01)

Di sini alpha adalah kepadatan neuron di lapisan tersembunyi. Untuk 40 neuron yang terlihat dan alpha 4, akan ada 160 di antaranya.Ada cara lain untuk menunjukkan secara langsung dengan angka. Perintah kedua menginisialisasi bobot secara acak

N (0, s i g m a)

$N (0, \ sigma)$ . Dalam kasus kami, sigma adalah 0,01.

Samler

Sampler adalah objek yang akan dikembalikan kepada kami oleh sampel dari distribusi kami, yang diberikan oleh fungsi gelombang pada ruang Hilbert. Kami akan menggunakan algoritma Metropolis-Hastings yang dijelaskan di atas, dimodifikasi untuk tugas kami:

 sampler = nk.sampler.MetropolisExchangePt( machine=machine, graph=graph, d_max=1, n_replicas=12 )

Lebih tepatnya, sampler adalah algoritma yang lebih rumit daripada yang saya jelaskan di atas. Di sini kita secara bersamaan memeriksa sebanyak 12 opsi secara paralel untuk memilih titik berikutnya. Tetapi prinsipnya, secara umum, adalah sama.

Pengoptimal

Ini menjelaskan pengoptimal yang akan digunakan untuk memperbarui bobot model. Menurut pengalaman pribadi bekerja dengan jaringan saraf di daerah yang lebih "akrab" bagi mereka, pilihan terbaik dan paling dapat diandalkan adalah keturunan gradien stochastic tua yang baik dengan momen (dijelaskan dengan baik di sini ):

 opt = nk.optimizer.Momentum(learning_rate=1e-2, beta=0.9)

Pelatihan

NetKet memiliki pelatihan baik tanpa guru (kasus kami) dan dengan guru (misalnya, yang disebut "kuantum tomografi", tetapi ini adalah topik dari artikel terpisah). Kami hanya menggambarkan "guru", dan hanya itu:

 vc = nk.variational.Vmc( hamiltonian=hamiltonian, sampler=sampler, optimizer=opt, n_samples=1000, use_iterative=True )

Variasi Monte Carlo menunjukkan bagaimana kita mengevaluasi gradien fungsi yang kita optimalkan. n_smaples adalah ukuran sampel dari distribusi kami yang dikembalikan oleh sampler.

Hasil

Kami akan menjalankan model sebagai berikut:

 vc.run(output_prefix=output, n_iter=1000, save_params_every=10)

Perpustakaan dibangun menggunakan OpenMPI, dan skrip harus dijalankan seperti ini: mpirun -n 12 python Main.py (12 adalah jumlah core).

Hasil yang saya terima adalah sebagai berikut:

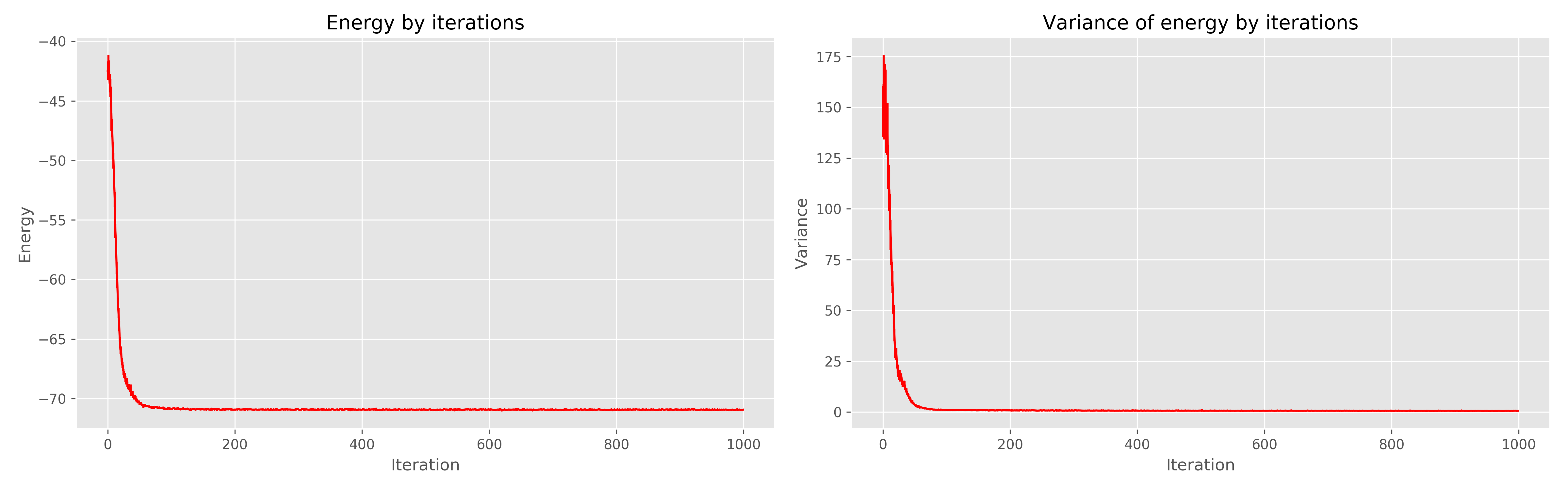
Di sebelah kiri adalah grafik energi dari era belajar, di sebelah kanan adalah penyebaran energi dari era belajar.
Dapat dilihat bahwa 1000 era jelas mubazir, 300 sudah cukup. Secara umum, ia bekerja sangat dingin, menyatu dengan cepat.

Sastra

Orús R. Pengantar praktis untuk jaringan tensor: Status produk Matrix dan proyeksi status pasangan terjerat // Sejarah Fisika. - 2014 .-- T. 349. - S. 117-158.
Carleo G., Troyer M. Memecahkan masalah banyak-tubuh kuantum dengan jaringan saraf tiruan // Sains. - 2017. - T. 355. - Tidak. 6325. - S. 602-606.
www.netket.org

Neural Quantum States - Representasi fungsi gelombang oleh jaringan saraf