Muon katalisis dalam hal kimia kuantum. Bagian II: elektronik vs. ikatan kimia muon

Mnogabukaff yang berpikir tentang kimia kuantum tentang prinsip katalisis muon: seberapa tepatnya muon menurunkan suhu plasma yang diinginkan. Dalam dua bagian (bagian pertama bisa dibaca di sini ).

Inti dari bagian kedua adalah sederhana: muon lebih berat dari elektron, sehingga memberikan ikatan kimia yang lebih kuat dan pendekatan inti yang lebih dekat, sehingga menurunkan suhu plasma yang diperlukan untuk memicu reaksi termonuklir.

Tetapi mereka yang ingin melihat rumus, grafik, dan melihat esensi konseptual kimia kuantum sebagaimana diterapkan pada molekul (kuasi) yang paling sederhana, diterima di bawah Cat.

Pendahuluan

Pada bagian pertama (lihat di sini ) kami memeriksa perbedaan antara atom hidrogen $$$\ mathrm {H} ^ \ cdot = \ mathrm {p ^ + e ^ -}$ dari mitra muon yang berat $$$\ mathrm {p} ^ + \ mu ^ -$ : dalam kasus kedua, muon akan diikat lebih kuat, dan itu akan duduk pada jarak yang lebih dekat dari proton. Pada saat yang sama, kami memeriksa beberapa hal penting yang kami perlukan di sini (bentuk orbital dan sistem atom unit).

Pada bagian kedua (mis., Di sini) kita akan mencoba memahami mengapa, bagaimana dan berapa suhu plasma yang diperlukan untuk menyalakan reaksi termonuklir akan menurun. Reaksi yang menarik minat kami adalah:

$$

$$\ mathrm {{} ^ nH + {} ^ m H \ rightarrow} \ \ text {kernel baru + energi}$$

di mana n, m = 1,2,3 masing-masing berhubungan dengan proton, deuterium dan tritium. Secara alami, nuklei ini memiliki muatan positif, jadi jika Anda mencoba mendekatkannya, mereka akan mulai menolak sesuai dengan hukum Coulomb (lihat bagian sebelumnya ), dan ini adalah penghalang yang sangat mencegah timbulnya reaksi fusi. Ngomong-ngomong, dalam kasus reaksi peluruhan nuklir, tolakan ini memiliki peran yang berlawanan, karena setelah pemisahan dari inti bersama, fragmen-fragmen, saling tolak satu sama lain, memperoleh energi kinetik tambahan, dan energi inilah yang dipanaskan di pembangkit listrik tenaga nuklir.

Untuk mengatasi penghalang Coulomb ini, diperlukan peningkatan suhu plasma ( T ), yang, sebagaimana semua orang ingat dari pelajaran sekolah MKT , dikaitkan dengan kecepatan partikel rata-rata dalam plasma ( v ) dengan rumus

$$

$$mv ^ 2 = 3k_ \ mathrm {B} T$$

di mana m adalah massa partikel, dan $$$k_ \ mathrm {B}$ - Konstanta Boltzmann .

Tapi, mari kita bayangkan bahwa kita telah menggabungkan dua inti hidrogen menjadi partikel tertentu, di mana mereka sudah berada dekat, dan oleh karena itu sisa penghalang bagi mereka sudah sangat kecil. Maka kita perlu mempercepat partikel-partikel ini secara signifikan (baca: kita perlu suhu yang lebih rendah) untuk menggabungkannya menjadi sesuatu yang baru. Dan peran seperti itu seharusnya memainkan ion perantara $$$(\ mathrm {{} ^ nH} \ mu ^ - \ mathrm {{} ^ mH}) ^ +$ , analog dari ion molekul hidrogen $$$\ mathrm {H} _2 ^ + = (\ mathrm {He ^ -H}) ^ +$ .
Setelah memeriksa perbedaan antara dua partikel ini, kita akan menyadari betapa efektifnya muon dalam menurunkan suhu pengapian fusi termonuklir.

Metode SUSU MO LKAO

Jadi, kami memiliki sistem molekuler kami, yang terdiri dari 2 inti hidrogen dengan muatan + e (satu modulo muatan elektron) dan satu partikel (elektron atau muon) dengan muatan - e . Sistem kami, sampai bertabrakan dengan partikel lain, diisolasi, dan oleh karena itu energinya dapat diuraikan menjadi bagian-bagian penyusunnya:

$$

$$E = T (\ mathrm {H} _1) + T (\ mathrm {H} _2) + \ underbrace {T (\ mathrm {e} ^ - / \ mu ^ -) + V (\ mathrm {H_1 \ text {from} H_2}) + V (\ mathrm {\ mathrm {e} ^ - / \ mu ^ - \ text {} \ mathrm {H} _1}) + V (\ mathrm {\ mathrm {e} ^ - - / \ mu ^ - \ text {k} \ mathrm {H} _2})} _ {E_ \ mathrm {e}}$$

dimana dua istilah pertama ( $$$T (\ mathrm {H} _1)$ dan $$$T (\ mathrm {H} _2)$ ) Adalah energi kinetik dari inti hidrogen, istilah ketiga ( $$$T (\ mathrm {e} ^ - / \ mu ^ -)$ ) Adalah energi kinetik dari partikel negatif (elektron atau muon), istilah keempat $$$V (\ mathrm {H_1 \ text {from} H_2})$ Adalah energi tolakan Coulomb dari hidrogen satu sama lain, dan dua sisanya adalah daya tarik Coulomb dari elektron / muon ke masing-masing proton. Dalam kasus umum, ini adalah masalah 3 tubuh, hanya masalah kuantum. Tentu saja, menyelesaikannya di dahi sangat sulit. Tapi, untungnya, nukleus setidaknya 1800 kali lebih berat dari elektron, dan 10 lebih berat dari muon, sehingga mereka akan bergerak lebih lambat dari partikel negatif kecil. Karena ini, Anda dapat menyelesaikan masalah pada gilirannya: pertama, temukan energi gerakan yang tidak terkait dengan pergerakan nuklei, mis. $$$E_ \ mathrm {e}$ dan kemudian energi penuh. Ini terlihat seperti ini.

1. Susunan inti hidrogen relatif satu sama lain dipilih, dan ini menentukan interaksi Coulomb antara mereka dan dengan elektron / muon. Potensi Coulomb $$$V (R) = k \ frac {q_1q_2} {R}$ hanya bergantung pada muatan partikel $$$q_i$ dan jarak di antara keduanya, jadi untuk semua isotop hidrogen, nilai ini akan sama. Kemudian masalah gerakan elektron / muon di bidang inti ini diselesaikan. Ini adalah tugas satu tubuh.
2. Energi-energi ini $$$E_ \ mathrm {e}$ dihitung untuk semua kemungkinan pengaturan inti relatif terhadap satu sama lain, dan ini akan menjadi energi potensial efektif gerak inti. Dalam kasus kami, kami perlu menghitung energi pada jarak yang berbeda relatif satu sama lain, sehingga potensi untuk pasangan inti selalu satu dimensi. Nah, maka kita hanya perlu menyelesaikan masalah dua tubuh dari gerakan dua isotop hidrogen relatif satu sama lain.

Jelas, akar masalah dengan kita adalah perhitungan energi elektron / muon di bidang inti $$$E_ \ mathrm {e}$ . Sebenarnya, ini adalah ikatan kimia: potensi tertentu yang mengikat inti bersama di tempat-tempat tertentu. Dan tugas menemukan energi ikatan kimia ini adalah yang utama dalam kimia kuantum.

Sayangnya, baik muon dan elektron adalah partikel kuantum, oleh karena itu, untuk menemukan energi ini, kita harus menggunakan metode mekanika kuantum. Faktanya, masalah kita tentang gerakan elektron / muon di bidang dua inti identik diselesaikan secara eksplisit (lihat di sini ), tetapi solusi ini sangat rumit dan hasilnya tidak sejelas dalam kasus atom mirip hidrogen. Oleh karena itu, kami akan mencoba membongkar pendekatan yang berbeda, pendekatan, yang berlaku untuk sistem apa pun. Inilah yang disebut metode orbital molekul sebagai kombinasi linear orbital atom, atau MO LKAO.

Mari kita lihat lebih dekat persamaan Schrödinger untuk gerakan elektron / muon di bidang inti hidrogen:

$$

$$\ hat {H} \ psi = \ underbrace {\ left (\ overbrace {- \ frac {1} {2m} (\ frac {\ partial ^ 2} {\ partial x ^ 2} + \ frac {\ partial ^ 2} {\ partial y ^ 2} + \ frac {\ partial ^ 2} {\ partial z ^ 2})} ^ {\ hat {T}} + \ overbrace {- \ frac {1} {R_1}} ^ {\ hat {V} _1} + \ overbrace {- \ frac {1} {R_2}} ^ {\ hat {V} _2} + \ overbrace {\ frac {1} {R}} ^ {\ hat {V } _ \ mathrm {HH}} \ kanan)} _ {\ hat {H}} \ psi = E \ psi$$

Persamaan ini ditulis dalam sistem atom unit (lihat PS di bagian sebelumnya ), oleh karena itu, muatan inti hidrogen dan elektron / muon masing-masing adalah +1, --1, massa elektron adalah m = 1, dan untuk muon m ≈207.

Dan jika Anda melihat lebih dekat, Anda dapat melihat bahwa di Hamiltonian Anda dapat memilih bagian yang terhubung murni dengan gerakan partikel negatif di sekitar hanya satu inti, yang hanya Hamiltonian dari atom hidrogen, dan ini dapat dilakukan dengan 2 cara:

$$

$$\ hat {H} = (\ overbrace {\ hat {T} + \ hat {V} _1} ^ {\ hat {H} _ {1}} + \ hat {V} _2 + \ hat {V} _ \ mathrm {HH}) = (\ overbrace {\ hat {T} + \ hat {V} _2} ^ {\ hat {H} _ {2}} + \ hat {V} _1 + \ hat {V} _ \ mathrm {HH})$$

Di luar Hamiltonian atom mirip hidrogen ( $$$\ hat {H} _i, \ i = $ 1.$ ) kami selalu memiliki 2 buah: energi interaksi elektron / muon dengan nukleus lain ( $$$\ hat {V} _j$ ) dan energi tolakan nuklir ( $$$\ hat {V} _ \ mathrm {HH}$ ) Yang kedua dari mereka tidak mempengaruhi pergerakan elektron sama sekali - itu hanya pergeseran energi dengan jumlah tertentu, tetapi interaksi elektron dengan nukleus lain adalah hal yang penting.
Kita dapat membayangkan bahwa setiap saat partikel kita hanya berputar di sekitar salah satu inti, dan interaksi dengan yang kedua hanyalah koreksi. Sebagai metode rotasi di sekitar salah satu nuklei, kita dapat mengasumsikan bahwa elektron / muon berada dalam kondisi ground (1s), fungsi gelombang yang sudah diketahui oleh kita dari bagian sebelumnya:

$$

$$| 1s \ rangle = \ frac {1} {\ sqrt {\ pi}} \ exp \ kiri (- \ frac {R} {R_1} \ kanan)$$

dimana $$$R_1$ Adalah jari-jari Bohr untuk sebuah partikel. Dalam hal elektron $$$R_1 = 1$ Boron (yang merupakan jari-jari Bohr untuk elektron, sama dengan sekitar 0,5 angstrom), dan dalam kasus muon $$$R_1 = \ frac {1} {m_ \ mu} \ approx \ frac {1} {207}$ .
Untuk memperkirakan fungsi gelombang elektron / muon dalam bidang 2 inti, kita dapat mencoba mengambil representasi berikut:

$$

$$\ psi \ approx c_1 | 1s_1 \ rangle + c_2 | 1s_2 \ rangle$$

dan kemudian masalah penyelesaian persamaan diferensial parsial kompleks dengan kami direduksi menjadi mencari 2 koefisien tidak diketahui c ₁ dan c ₂ . Ini adalah orbital yang sangat molekuler yang disajikan sebagai penjumlahan dengan koefisien (kombinasi linear dari ilmiah) orbital 1s atom.

Secara alami, kita membutuhkan persamaan untuk parameter ini. Dan mendapatkannya cukup sederhana jika Anda mengganti perkiraan ini dalam persamaan Schrödinger $$$\ hat {H} \ psi = E \ psi$ :

$$

$$\ hat {H} (c_1 | 1s_1 \ rangle + c_2 | 1s_2 \ rangle) = c_1 \ hat {H} | 1s_1 \ rangle + c_2 \ hat {H} | 1s_2 \ rangle = E (c_1 | 1s_1 \ rangle + c_2 | 1s_2 \ rangle) = c_1 E | 1s_1 \ rangle + c_2 E | 1s_2 \ rangle$$

Sebenarnya, kami ingin rasio ini dipenuhi di mana-mana, jadi kami entah bagaimana dapat menghitung nilai rata-rata dari semua ini. Kami mengalikan persamaan ini di sebelah kiri oleh $$$<1s_1 |$ dan $$$<1s_2 |$ dan mengintegrasikan semua koordinat. Sebagai hasilnya, kami memperoleh sistem 2 persamaan linear, di mana perlu untuk menemukan koefisien c ₁ , c ₂ dan energi E :

$$

$$\ begin {pmatrix} \ langle 1s_1 | \ hat {H} | 1s_1 \ rangle & \ langle 1s_1 | \ hat {H} | 1s_2 \ rangle \\ \ langle 1s_2 | \ hat {H} | 1s_1 \ rangle & \ langs 1s_2 | \ hat {H} | 1s_2 \ rangle \\ \ end {pmatrix} \ begin {pmatrix} c_1 \\ c_2 \ end {pmatrix} = E \ begin {pmatrix} \ langle 1s_1 | 1s_1 \ rangle & \ langle 1s_1 | 1s_2 \ rangle \\ \ langle 1s_2 | 1s_1 \ rangle & \ langle 1s_2 | 1s_2 \ rangle \\ \ end {pmatrix} \ begin {pmatrix} c_1 \\ c_2 \ end {pmatrix}$$

Siapa pun yang telah mempelajari aljabar linier akan mengenali masalah nilai eigenvektor-eigen umum. Sebelum menyelesaikannya, kami akan menganalisis apa elemen dari 2 matriks, tuta yang ada, sama dengan (dan pada saat yang sama kami memperkenalkan penunjukan singkat mereka dengan satu huruf).

• Mari kita mulai dengan yang paling sederhana: $$$\ langle 1s_1 | 1s_1 \ rangle = \ langle 1s_2 | 1s_2 \ rangle = 1$ - ini adalah normalisasi fungsi gelombang, dan seperti yang kita ingat, probabilitas total untuk menemukan elektron / muon setidaknya 1 di suatu tempat.
• $$$\ langle 1s_1 | 1s_2 \ rangle = \ langle 1s_2 | 1s_1 \ rangle = S$ - ini yang disebut tumpang tindih integral, menunjukkan bagaimana awan elektron 1s tumpang tindih untuk masing-masing atom.
• $$$\ langle 1s_1 | \ hat {H} | 1s_1 \ rangle = \ langle 1s_2 | \ hat {H} | 1s_2 \ rangle = \ alpha$ . Integral ini terdiri dari beberapa bagian:
  

  $$

  $$\ langle 1s_1 | \ hat {H} | 1s_1 \ rangle = \ underbrace {\ langle 1s_1 | \ hat {H} _1 | 1s_1 \ rangle} _ {- \ frac {m} {2}} + \ langle 1s_1 | \ hat {V} _2 | 1s_1 \ rangle + \ frac {1} {R}$$
  
  
• $$$\ langle 1s_1 | \ hat {H} | 1s_2 \ rangle = \ langle 1s_2 | \ hat {H} | 1s_1 \ rangle = \ beta$ . Ini mirip:
  

  $$

  $$\ langle 1s_2 | \ hat {H} | 1s_1 \ rangle = \ underbrace {\ langle 1s_2 | \ overbrace {\ hat {H} _1 | 1s_1 \ rangle} ^ {- \ frac {m} {2} | 1s_1 \ rangle}} {{\ frac {m} {2} S} + \ langle 1s_2 | \ hat {V} _2 | 1s_1 \ rangle + \ frac {S} {R}$$
  
  yaitu energi atom seperti hidrogen dan tolakan internuklear, diskalakan oleh integral tumpang tindih (istilah pertama dan terakhir), dan, seolah-olah, energi elektron / muon melompat dari satu atom ke atom lain.
  

Mari kita temukan ekspresi untuk energi ion seperti hidrogen dari persamaan yang ditulis ulang sebagai

$$

$$\ begin {pmatrix} \ alpha & \ beta \\ \ beta & \ alpha \ end {pmatrix} \ begin {pmatrix} s_1 \\ c_2 \ end {pmatrix} = E \ begin {pmatrix} 1 & S \\ S & 1 \ end {pmatrix} \ begin {pmatrix} c_1 \\ c_2 \ end {pmatrix}$$

Untuk menemukan energi yang Anda butuhkan untuk menyelesaikan persamaan:

$$

$$\ det \ begin {pmatrix} \ alpha -E & \ beta -ES \\ \ beta - ES & \ alpha -E \ end {pmatrix} = (\ alpha -E) ^ 2 - (\ beta - ES) ^ 2 = 0$$

di mana "det" menunjukkan penentu (penentu matriks, dalam bahasa Rusia).

Solusi persamaan kuadratik ini berkenaan dengan E adalah:

$$

$$E_ \ pm = \ frac {\ alpha \ pm \ beta} {1 \ pm S} = - \ frac {m} {2} + \ frac {1} {R} + \ frac {\ langle 1s_1 | \ hat {V} _2 | 1s_1 \ rangle \ pm \ langle 1s_2 | \ hat {V} _2 | 1s_1 \ rangle} {1 \ pm S}$$

Bagian pertama jelas adalah energi atom, yang kedua adalah tolakan internuklear, penghalang Coulomb yang sama yang mencegah pengapian reaksi termonuklir, dan struktur kompleks terakhir harus ditangani.

Jika kita membuang tolakan internuklear, yang hanya merupakan titik referensi untuk energi elektron / muon, kita mendapatkan bahwa kita memiliki dua keadaan dengan energi

$$

$$\ epsilon_ \ pm = - \ frac {m} {2} + \ frac {\ langle 1s_1 | \ hat {V} _2 | 1s_1 \ rangle \ pm \ langle 1s_2 | \ hat {V} _2 | 1s_1 \ rangle} {1 \ pm S}$$

Karena keduanya berfungsi gelombang $$$| 1s_1 \ rangle$ dan $$$| 1s_2 \ rangle$ - positif, dan $$$\ hat {V} _i <0$ (Karena partikel negatif selalu tertarik ke positif), maka $$$\ epsilon_ + <- \ frac {m} {2}$ (energi satu atom), dan $$$\ epsilon _-> - \ frac {m} {2}$ , yaitu kami mendapatkan gambaran standar orbital molekul:



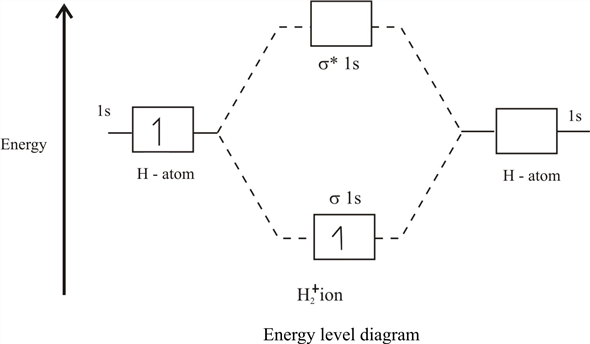
Turunkan orbital dengan energi $$$E _ +$ disebut mengikat, dan bagian atas (dengan energi $$$E _-$ ) - anti-binding, atau melonggarkan. Akibatnya, jika sebuah elektron / muon duduk di orbital molekul yang lebih rendah, maka ia mendapat manfaat dari terbang di sekitar 2 inti daripada di sekitar satu, dan dengan gerakannya ia menurunkan energi total sistem. Dan ini adalah ikatan kimia yang sangat ajaib yang menyaring tolakan internuklear, yang memungkinkan inti untuk bersebelahan selama beberapa waktu.

Dan di sini, integral ikatan kimia harus dihitung untuk memahami seberapa dekat inti hidrogen diizinkan. Faktanya, ketiga integral yang dicari dihitung secara analitis, tetapi sangat ambeien dan rumit (siapa pun yang tertarik, lihat Bab 9 dalam buku Kimia Kuantum Flary ). Oleh karena itu, kami akan pergi dengan cara yang berbeda, lebih sederhana, dan menghitung integral ini secara numerik menggunakan metode Monte Carlo.

Metode Metropolis

Saya melihatnya sebagai sangat logis dalam teks tentang energi termonuklir untuk membayar upeti kepada kakeknya: atom militer, dan lebih khusus lagi, proyek Manhattan . Dari dia lah metode Monte Carlo tumbuh, dan khususnya algoritma Metropolis , salah satu penulisnya, Edward Teller, adalah "bapak bom hidrogen" (yaitu, orang yang meluncurkan fusi termonuklir di Atol Envetok).


Secara umum, kami akan menganalisis esensi dari metode ini. Ini dimaksudkan untuk tugas mekanik statistik. Distribusi utama di dalamnya adalah distribusi Boltzmann: probabilitas mendeteksi suatu sistem dalam keadaan tertentu adalah $$$\ exp (- \ beta E)$ , $$$\ beta ^ {- 1} = k_ \ mathrm {B} T$ . Dan nilai yang diamati dari beberapa parameter A untuk sistem dalam kesetimbangan termodinamika sama dengan integral

$$

$$\ langle A \ rangle = \ frac {1} {Z} \ int A (q) \ exp (- \ beta E (q)) dq$$

di mana q adalah koordinat yang mengukur keadaan sistem (misalnya, koordinat / momen dari partikel), dan Z adalah faktor normalisasi yang disebut fungsi partisi:

$$

$$Z = \ int \ exp (- \ beta E (q)) dq$$

Jika ada begitu banyak partikel dalam sistem, maka menghitung tidak ada integral di dahi benar-benar tidak realistis. Metode Monte Carlo yang naif, di mana kita cukup memilih sekelompok koordinat q acak, juga tidak akan memberikan sesuatu yang bermakna jika benar-benar ada kemungkinan keadaan sistem yang kemungkinannya terjadi. $$$\ exp (- \ beta E)$ jelas bukan nol, sangat sedikit. Dan justru untuk kasus-kasus seperti itu kita membutuhkan sampel dengan signifikansi, di mana kita mengizinkan algoritma untuk sampel hanya tempat yang cukup mungkin di ruang keadaan.

Algoritma Metropolis terlihat sebagai berikut.

1. Saat memulai simulasi, kami memilih beberapa perkiraan awal di ruang konfigurasi $$$\ mathbf {q} ^ {(0)}$ dan beberapa vektor kenaikan maksimum yang mungkin $$$\ delta \ mathbf {q}$ . Pada titik awal, kami menghitung energi sistem $$$E ^ {(0)} = E (\ mathbf {q} ^ {(0)})$ (baca - probabilitas $$$p = \ exp (- \ beta E ^ {(0)})$ )
2. Konfigurasi baru pada langkah ke - n adalah sebagai berikut.
   
   1. Hitung energi konfigurasi percobaan $$$E_ \ mathrm {trial} = E (\ mathbf {q} _ \ mathrm {trial})$ (mis. probabilitas $$$p_ \ mathrm {trial} = \ exp (- \ beta E_ \ mathrm {trial})$ )
   2. Dan kemudian kita membandingkan probabilitas lama $$$p ^ {(n)}$ dengan persidangan $$$p_ \ mathrm {percobaan}$
      
      
      • jika konfigurasi baru memiliki probabilitas lebih besar atau sama ( $$$\ frac {p_ \ mathrm {trial}} {p ^ {(n)}} \ geq 1$ ), atau, ekuivalen, energi dari titik baru lebih rendah atau sama dengan yang lama ( $$$E_ \ mathrm {percobaan} \ leq E ^ {(n)}$ ), maka titik baru diterima dan sistem masuk ke dalamnya ( $$$q ^ {(n + 1)} = q_ \ mathrm {trial}$ ),
      • jika konfigurasi percobaan lebih tinggi dalam energi ( $$$E_ \ mathrm {percobaan}> E ^ {(n)}$ ), yang setara $$$\ frac {p_ \ mathrm {trial}} {p ^ {(n)}} <1$ , maka dalam hal ini kita menghasilkan angka acak $$$P \ in [0; 1)$ dari distribusi yang seragam, dan membandingkannya dengan rasio probabilitas, yang merupakan probabilitas transisi. Jika $$$P <\ frac {p_ \ mathrm {trial}} {p ^ {(n)}}$ , maka kami menerima poin baru, dan jika tidak ( $$$P \ geq \ frac {p_ \ mathrm {trial}} {p ^ {(n)}}$ ), lalu kami tolak, dan sistem tetap dalam konfigurasi lama ( $$$q ^ {(n + 1)} = q ^ {(n)}$ ) ...
      
      
   
   
3. Mengambil banyak langkah sesuai dengan algoritma di atas, kami mencicipi bagian penting (mis., Sangat penting) dari kemungkinan ruang konfigurasi sistem. Yang tidak terpisahkan dari minat kami dihitung dengan rumus:
   $$$\ langle A \ rangle = \ frac {1} {Z} \ int A (\ mathbf {q}) \ exp (- \ beta E (\ mathbf {q})) d \ mathbf {q} = \ frac { 1} {N} \ sum_ {n = 0} ^ {N} A (\ mathbf {q} ^ {(n)})$
   

Ini adalah cara kerja algoritma Metropolis.

Dan sekarang perlu untuk menyesuaikannya dengan perhitungan 3 integral yang menarik bagi kita. Mari kita lihat lebih detail.

• $$$S (R) = \ langle 1s_2 | 1s_1 \ rangle = \ int \ Limit _ {- \ infty} ^ {+ \ infty} \ int \ limit _ {- \ infty} ^ {+ \ infty} \ int \ limit _ {- - \ infty} ^ {+ \ infty} \ overbrace {\ underbrace {\ frac {1} {\ sqrt {\ pi}} \ exp (-m \ underbrace {| \ mathbf {r} - \ mathbf {r} _2 | } _ {R_2})} _ {1s_2}} ^ {A (\ mathbf {r})} \ cdot \ overbrace {\ underbrace {\ frac {1} {\ sqrt {\ pi}} \ exp (-m \ underbrace {| \ mathbf {r} - \ mathbf {r} _1 |} _ {R_1})} _ {1s_1}} ^ {p (\ mathbf {r})} dx dy dz$ dimana $$$\ mathbf {r} = (x, y, z) ^ \ mathbf {T}$ - koordinat elektron / muon, $$$\ mathbf {r} _i = (x_i, y_i, z_i) ^ \ mathbf {T}$ Apakah koordinat inti hidrogen, dan $$$R_i = | \ mathbf {r} - \ mathbf {r} _i | = \ sqrt {(x-x_i) ^ 2 + (y-y_i) ^ 2 + (z-z_i) ^ 2}$ - jarak antara partikel positif dan negatif,
  
• $$$\ langle 1s_1 | \ hat {V} _2 | 1s_1 \ rangle = - \ int \ limit _ {- \ infty} ^ {+ \ infty} \ int \ limit _ {- \ infty} ^ {+ \ infty} \ int \ batas _ {- \ infty} ^ {+ \ infty} \ overbrace {\ underbrace {\ frac {1} {\ sqrt {\ pi}} \ exp (-mR_1)} _ {1s_1} \ frac {1} {R_2} } ^ {A (\ mathbf {r})} \ cdot \ overbrace {\ underbrace {\ frac {1} {\ sqrt {\ pi}} \ exp (-mR_1)} _ {1s_1}} ^ {p (\ mathbf {r})} dxdydz$
• $$$\ langle 1s_2 | \ hat {V} _2 | 1s_1 \ rangle = - \ int \ limit _ {- \ infty} ^ {+ \ infty} \ int \ limit _ {- \ infty} ^ {+ \ infty} \ int \ batas _ {- \ infty} ^ {+ \ infty} \ overbrace {\ underbrace {\ frac {1} {\ sqrt {\ pi}} \ exp (-mR_2)} _ {1s_2} \ frac {1} {R_1} } ^ {A (\ mathbf {r})} \ cdot \ overbrace {\ underbrace {\ frac {1} {\ sqrt {\ pi}} \ exp (-mR_1)} _ {1s_1}} ^ {p (\ mathbf {r})} dxdydz$

Dapat dilihat bahwa, jika kita menghitung fungsi 1s dari salah satu atom untuk probabilitas p ,


maka segala sesuatu yang lain di bawah tanda integral (fungsi gelombang kedua dan dalam 2 dari 3 kasus potensi tarikan elektron / muon ke inti) akan menjadi fungsi yang nilai rata-ratanya dihitung. Satu-satunya hal yang harus dilakukan, berbeda dengan perhitungan biasa dengan metode Metropolis, adalah meluruskan normalisasi integral. Faktanya adalah normalisasi standar akan aktif

$$

$$Z = \ int \ Limit _ {- \ infty} ^ {+ \ infty} \ int \ Limit _ {- \ infty} ^ {+ \ infty} \ int \ Limit _ {- \ infty} ^ {+ \ infty} \ exp (-m R) dx dy dz = 4 \ pi \ int \ limit_ {0} ^ {+ \ infty} \ exp (-m R) R ^ 2 dR = \ frac {8 \ pi} {m ^ 3}$$

Dan kita perlu normalisasi $$$\ sqrt {\ langle 1s_1 | 1s_1 \ rangle}$ dimana

$$

$$\ langle 1s_1 | 1s_1 \ rangle = \ int \ Limit _ {- \ infty} ^ {+ \ infty} \ int \ Limit _ {- \ infty} ^ {+ \ infty} \ int \ limit _ {- \ infty} ^ {+ \ infty} \ exp (-2 m R) dx dy dz = 4 \ pi \ int \ limit_ {0} ^ {+ \ infty} \ exp (-2m R) R ^ 2 dR = \ frac {\ pi} {m ^ 3}$$

Ini berarti bahwa setiap integral yang dihitung menurut Metropolis perlu dikalikan dengan faktor

$$

$$\ frac {Z} {\ sqrt {\ langle 1s_1 | 1s_1 \ rangle}} = 8 \ sqrt {\ frac {\ pi} {m ^ 3}}$$

Ini sudah dapat diatur dalam bentuk skrip tertentu, misalnya, dengan Python (misalnya, kode di bawah).


Dengan menggunakan perhitungan seperti itu, kita akhirnya dapat membandingkan energi potensial dalam ion hidrogen $$$\ mathrm {H} _2 ^ +$ dan padanan muonnya.

$$$\ mathrm {H_2 ^ + = p ^ + e ^ - p ^ +}$ vs. $$$\ mathrm {p ^ + \ mu ^ - p ^ +}$

Jadi, dipersenjatai dengan sebuah skrip, kita dapat menghitung permukaan energi potensial dari pendekatan inti hidrogen yang terikat oleh elektron dan muon. Sebagai titik referensi energi, kita mengambil atom yang terdilusi secara tak terbatas dari satu sama lain (mis., $$$-m / 2$ yang sama dengan potensial pada jarak antara inti $$$R = + \ infty$ )

Dalam kasus elektron, potensi dekat minimum terlihat seperti ini:



Minimum terjadi pada jarak sekitar 2 Boron (mis., Kira-kira jumlah dari 2 jari-jari atom), dan energi disosiasi molekul menjadi fragmen adalah sekitar 0,06 Hartree, yang sesuai dengan pemanasan hingga sekitar 20.000 derajat Kelvin (atau Celsius, tidak masalah di sini). Untuk mengonversi energi, saya sarankan menggunakan sumber daya online, seperti ini .

Situasi serupa dengan ion hidrogen yang terikat secara muonal:



Karena jari-jari Bohr untuk hidrogen muon lebih kecil (lihat bagian sebelumnya ), inti hidrogen juga duduk sekitar 200 kali lebih dekat pada energi potensial minimum. Energi pemecahan molekul ini sudah lebih dari 10 Hartree, yang sesuai dengan suhu lebih dari tiga derajat lyam ( $$$\ approx (3.2 \ cdot 10 ^ 6) ^ \ circ$ )

Untuk penyalaan, reaksi biasanya memerlukan suhu urutan 10 ⁸ K , yaitu sekitar 320 Hartree. Mari kita lihat pada jarak apa energi yang sama dicapai dalam kasus ion divodoron biasa dan dalam kasus versi muonnya:



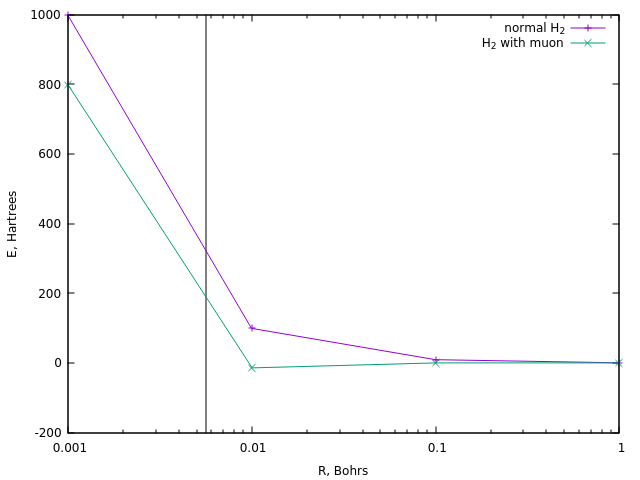
Dalam kasus yang pertama, ini sesuai dengan jarak sekitar 0,0058 Boron (garis vertikal).

Jarak yang serupa dalam hidrogen muon dicapai pada energi sekitar 190 Ha, yaitu sekitar satu setengah kali lebih sedikit. Dan ini adalah perkiraan paling sederhana dari suhu katalisis muon.

Tetapi pada kenyataannya, semuanya akan menjadi lebih dingin. Faktanya adalah jika partikel stabil terbentuk $$$\ mathrm {({} ^ mH (\ mu ^ -) {} ^ nH) ^ +}$ , maka nuklei ini, selagi muon hidup, akan berosilasi satu sama lain. Dan di sini tunneling dari keadaan "dua atom hidrogen" ke keadaan "core yang lebih berat" dapat terjadi, dan kemungkinan tunneling tergantung pada panjang tunneling yang diperlukan d kira-kira sama $$$p ^ {- d}$ , sehingga membawa dua inti lebih dekat bersama oleh muon kita akan sangat meningkatkan kemungkinan jalannya reaksi ini. Sayangnya, perkiraan efek ini tidak lagi membutuhkan kimia kuantum, tetapi fisika nuklir, sehingga bagian diskusi ini berada di luar cakupan tulisan ini. Jadi kita akan berhenti.

PS Mengapa tidak sesederhana itu?

Bahkan, untuk membentuk partikel-partikel ini tidak begitu sederhana dalam kondisi plasma. Faktanya adalah bahwa jika kita bertabrakan dua partikel, maka total energi mereka jelas melebihi energi disosiasi (atau ionisasi, dalam kasus inti + elektron / muon), jadi ketika mereka bertabrakan, mereka tidak membentuk partikel yang stabil (atom, ion, molekul), tetapi terbang dengan saling melewati. Untuk tetap bersatu, mereka perlu membuang energi surplus, dan untuk ini kita membutuhkan tambahan ketiga yang akan mengambil energi ini. Ini bisa berupa foton, atau sejenis partikel kiri yang terbang di dekatnya, tetapi yang utama adalah bahwa kondisinya harus berkontribusi pada entrainment energi berlebih ini.

PPS

Jika Anda memiliki komentar / klarifikasi / pertanyaan, tulis komentar atau di PM. Saya akan memperbaiki segalanya, saya akan menjawab dan menjelaskan semuanya.