Geekly articles weekly

Jenis infinitas dan batang otak


Artikel ini merupakan kelanjutan dari artikel tentang jumlah besar . Tetapi sekarang kita akan melangkah lebih jauh - dalam ketidakterbatasan tanpa batas.

Untuk ini kita perlu ZFC - teori himpunan Zermelo, Frenkel + Choice. Pilihan adalah aksioma pilihan, aksioma teori himpunan yang paling kontroversial. Dia layak mendapat artikel terpisah. Diasumsikan bahwa Anda tahu apa "kekuatan" himpunan itu. Jika tidak, maka google, pasti ini dinyatakan lebih baik daripada yang saya bisa. Di sini saya hanya akan mengingatkan beberapa

Fakta yang diketahui


  • Kekuatan satu set bilangan bulat dilambangkan dengan $ \ aleph_0 $ . Ini adalah kekuatan tak terbatas pertama, perangkat seperti itu disebut dapat dihitung.
  • Kekuatan setiap subset bilangan bulat tak terbatas adalah sederhana, genap, dll. - juga dapat dihitung.
  • Himpunan bilangan rasional, yaitu fraksi p / q, juga dapat dihitung, dapat dilewatkan oleh ular.
  • Untuk daya apa pun, ada operasi powerset - himpunan semua himpunan bagian yang menciptakan lebih banyak kekuatan daripada yang asli. Kadang-kadang operasi ini disebut sebagai menaikkan dua daya, yaitu $ powerset (\ aleph_0) = 2 ^ {\ aleph_0} = \ aleph_c $ . Powerset dari kekuatan dihitung adalah kekuatan kontinum.
  • Kekuatan kontinum dimiliki oleh: segmen yang terbatas dan tak terbatas, angka planar dan volumetrik, dan bahkan ruang n-dimensi secara keseluruhan
  • Untuk matematika biasa, kekuatan berikut, $ powerset (\ aleph_c) $ praktis tidak diperlukan, biasanya semua pekerjaan terjadi dengan set yang dapat dihitung dan set daya kontinum

Sekarang

Fakta yang sedikit diketahui


Di ZFC, tidak semua koleksi elemen dapat diatur. Ada koleksi yang sangat luas sehingga tidak mungkin untuk membiarkannya menjadi set, paradoks muncul. Secara khusus, " set semua set " bukan set. Namun, ada teori himpunan di mana himpunan tersebut diizinkan.

Lebih jauh Tetapkan Teori ... Objek Apa? Angka? Sebuah apel? Jeruk? Anehnya, ZFC tidak membutuhkan benda apa pun. Ambil set kosong {} dan sepakati bahwa itu berarti 0. 1 dilambangkan dengan {{}} deuce sebagai {{{}}} dan seterusnya. {5,2} adalah {{{{{{}}}}}}, {{{}}}}. Dengan menggunakan bilangan bulat, kita dapat membuat yang asli, dan koleksi yang asli dapat membuat bentuk apa saja.

Jadi teori yang ditetapkan adalah ... bagaimana mengatakannya ... teori kosong. Teori ini tentang apa-apa. Lebih tepatnya, tentang bagaimana Anda dapat bersarang (bersarang, yaitu saling menempel).

Satu-satunya operasi yang didefinisikan dalam teori himpunan adalah $ \ dalam $ - simbol kepemilikan. Tetapi bagaimana dengan unifikasi, eksklusi, kesetaraan, dll.? Ini semua adalah makro, misalnya:

$ (A = B) \ equiv \ forall x ((x \ dalam A) = (x \ dalam B)) $


Artinya, dalam terjemahan ke bahasa Rusia, dua set dianggap sama ketika, ketika menguji setiap elemen untuk menjadi milik mereka, kita akan mendapatkan hasil yang sama

Set tidak dipesan, tetapi ini bisa diperbaiki: biarkan pasangan yang dipesan (p, v) menjadi {{p}, {p, v}}. Inelegant dari sudut pandang programmer, tetapi cukup untuk seorang matematikawan. Sekarang himpunan semua pasangan param-value menetapkan suatu fungsi, yang sekarang juga disetel! Et voila! semua analisis matematis, yang bekerja pada level bahasa orde kedua , karena ia tidak berbicara tentang keberadaan angka , tetapi tentang keberadaan fungsi , runtuh menjadi bahasa orde pertama!

Dengan demikian, teori himpunan adalah teori yang buruk tanpa objek dan dengan satu ikon relasi, yang memiliki kekuatan yang benar-benar mengerikan - tanpa asumsi baru, ia menghasilkan dari aritmatika formal, bilangan real, analisis, geometri, dan banyak lagi. Ini adalah semacam matematika TOE.

Hipotesis Continuum - CH


Apakah ada kekuatan di antara keduanya? $ \ aleph_0 $ dan $ 2 ^ {\ aleph_0} $ ? Cantor tidak dapat menyelesaikan masalah ini, "raja ahli matematika" Hilbert memuji pentingnya hal ini, tetapi hanya kemudian terbukti bahwa hipotesis ini tidak dapat dibuktikan atau dibantah. Dia tidak tergantung pada ZFC.

Ini berarti Anda dapat membuat dua matematika yang berbeda: satu dengan ZFC + CH, yang lainnya dengan ZFC + (bukan CH). Bahkan, lebih dari dua. Misalkan kita menolak CH, artinya, kita akan percaya bahwa di antara $ \ aleph_0 $ dan $ 2 ^ {\ aleph_0} $ masih ada kekuatan. Ada berapa banyak? Satu dua? Godel percaya bahwa hanya satu. Tetapi, ternyata, anggapan bahwa ada 2, 17, 19393493 di antaranya tidak mengarah pada kontradiksi. Jumlah apa pun, tetapi tidak terbatas!

Ketika dalam aritmatika formal kita menemukan pernyataan yang tidak dapat dibuktikan, untuk alasan tertentu kita tahu bahwa, bagaimanapun, pernyataan ini, meskipun tidak dapat dibuktikan, sebenarnya benar atau salah. Dalam teori himpunan ini tidak bekerja, kita benar-benar mendapatkan ahli matematika yang berbeda. Bagaimana berhubungan dengan ini? Ada tiga pendekatan filosofis:

Formalisme: mengapa, pada kenyataannya, terkejut? Kami menetapkan aturan permainan simbol, aturan berbeda - hasil berbeda. Tidak perlu mencari masalah yang tidak ada

Platonisme: Tetapi bagaimana kemudian menjelaskan bahwa teori yang sama sekali berbeda, seperti ZFC dan Yayasan Baru, yang dibangun di atas prinsip yang sama sekali berbeda, hampir selalu memberikan hasil yang sama? Apakah ini berarti bahwa di balik formula adalah semacam kenyataan yang sedang kita pelajari? Pandangan ini dipegang, misalnya, oleh Godel

Multiverse: Kita dapat memiliki banyak aksioma, terkadang memberikan hasil yang sama, terkadang tidak. Kita harus memahami gambar secara keseluruhan - jika warna dikaitkan dengan sistem aksioma yang berbeda, maka pohon efek berwarna adalah matematika. Jika ada sesuatu yang benar di mana-mana - itu putih, tetapi ada juga cabang berwarna.

Lebih tinggi dan lebih tinggi.


Di masa depan, untuk kesederhanaan, kami akan menerima hipotesis kontinum, yaitu $ powerset (\ aleph_0) = \ aleph_1 = \ aleph_c $ - sangat nyaman. Bahkan, kita juga akan menerima aksioma yang lebih kuat, hipotesis kontinum umum bahwa antara x dan powerset (x) tidak pernah ada kekuatan menengah. Sekarang kita beralih ke powerset dan semuanya sederhana:

$ \ aleph_0 \ rightarrow \ aleph_1 \ rightarrow \ aleph_2 \ rightarrow ... \ rightarrow \ aleph_ {36463634} \ rightarrow $


Seberapa jauh kita bisa melangkah? Setelah jumlah iterasi yang tak terbatas, kita sampai $ \ aleph_ \ omega $ - Kekuasaan tak terbatas agar! Ngomong-ngomong, keberadaannya tidak jelas bagi Cantor. Tapi sedetik! Bagaimanapun, fungsi powerset selalu ditentukan, oleh karena itu $ \ aleph_ \ omega $ tidak bisa menjadi yang terakhir!

$ \ aleph_ \ omega \ rightarrow \ aleph _ {\ omega + 1} \ rightarrow \ aleph _ {\ omega + 2} \ rightarrow ... $


Untuk mendapatkan $ \ aleph _ {\ omega + 3} $ perlu mengulangi powerset infinity dan tiga kali lagi . Apakah Anda sudah mulai menghancurkan atap? Atau yang akan terjadi. Karena sekali lagi, setelah mengulangi pengesetan sejumlah kali tanpa batas, kita dapat melakukannya $ \ aleph _ {\ omega + \ omega} = \ aleph _ {\ omega2} $ , setelah itu, secara alami, $ \ aleph _ {\ omega2 + 1} $

Setelah mencapai jumlah tak terbatas beberapa kali , kami memperoleh indeks $ \ omega ^ 2 $ . Bagaimana Anda menyukai kekuatan ini, misalnya: $ \ aleph _ {\ omega ^ 3 + \ omega ^ 2 + \ omega4 + 48745} $ ? Sementara kami mengulangi powerset ke daftar tata cara, berikut adalah tata cara awal:

gambar

tetapi ada banyak, banyak lagi. Jadi kita akan langsung melewatinya dan melakukannya

Langkah besar segera


Perhatian! Apa yang tertulis di bawah ini mungkin berbahaya bagi otak Anda! Kita mengulangi powerset beberapa kali, tetapi tidakkah kita melambai ke kontinum ? Jujur, saya sendiri sedikit sosis dari kenyataan bahwa siklus dapat dilakukan secara kontinu kali, tetapi teori himpunan membutuhkan keberadaan

$ \ aleph _ {\ aleph_1} $


Selanjutnya kita akan pergi lebih cepat:

$ \ aleph _ {\ aleph_1} \ rightarrow \ aleph _ {\ aleph_2} ... \ rightarrow \ aleph _ {\ aleph_ \ omega} = \ aleph _ {\ aleph_ \ aleph} \ rightarrow $


Alef terakhir memiliki indeks nol, tetapi lateks lokal tidak memungkinkan untuk dimasukkan - ada terlalu banyak level. Tapi yang utama adalah bahwa Anda mengerti, tidak peduli berapa banyak kekuatan mengerikan baru yang akan kita buat, kita dapat mengatakan - ya, ini hanya pengulang , dan menempatkan seluruh konstruksi ini dalam bentuk indeks ke Aleph baru. Sekarang kapasitas tumbuh seperti bola salju, kita tidak bisa dihentikan, piramida Alephs lebih tinggi dan kita dapat menciptakan kekuatan apa pun ... Atau tidak?

Kekuatan yang tidak terjangkau


Bagaimana jika ada kekuatan yang begitu besar $ \ theta $ bahwa tidak peduli bagaimana kita berusaha mencapainya "dari bawah", membangun struktur dari Alephs, kita tidak akan mencapainya? Ternyata keberadaan kekuatan semacam itu tidak tergantung pada ZFC. Anda bisa menerima keberadaannya atau tidak.

Saya mendengar bisikan pisau Occam ... Tidak, tidak. Matematikawan berpegang pada prinsip yang berlawanan, yang disebut maximalisme ontologis - biarkan segala sesuatu yang mungkin ada. Tetapi setidaknya ada dua alasan mengapa saya ingin menerima hipotesis ini.

  • Pertama, ini bukan kekuatan tak terjangkau pertama yang kita tahu. Pertama ... ini adalah kekuatan penghitungan yang sudah dikenal. Anehnya, ia memiliki semua properti yang tidak dapat dijangkau - hanya tidak lazim menyebutnya sebagai:
  • Tidak ada cara untuk mendapatkan kekuatan tak terbatas "dari bawah" - tidak menambahkan elemen beberapa kali hingga terbatas, juga tidak mengulangi powerset () berkali-kali, menggunakan set terbatas untuk seeding, Anda tidak akan mendapatkan infinity. Untuk mendapatkan tak terbatas, Anda harus sudah memilikinya di suatu tempat.
  • Keberadaan kekuatan tanpa batas diperkenalkan oleh aksioma khusus - aksioma ketidakterbatasan. Tanpa itu, keberadaan kekuatan tak terbatas tidak dapat dibuktikan.


Kedua: jika kita menolak aksioma ketidakterbatasan, kita mendapatkan FinSet, teori himpunan mainan sederhana dengan himpunan terbatas. Mari kita tuliskan semua perangkat ini ( model teori )

{}
{{}}
{{{}}, {}}
{{{{}}}}
{{{{}}}, {{}}}
{{{{}}}, {{}}}
{{{{}}}, {{}}, {}}
...

Dan kita mendapatkan ... satu set himpunan tak terbatas ... Yaitu, model teori himpunan terbatas tak terbatas, dan memainkan peran "himpunan semua himpunan" di dalamnya. Mungkin ini akan membantu untuk memahami mengapa teori tidak dapat berbicara tentang "set semua set" - set seperti itu selalu ada sebagai model di luar teori dan memiliki sifat lain selain set di dalam. Anda tidak dapat menambahkan infinite ke teori himpunan terbatas.

Dan ya $ \ theta $ itu adalah "banyak sekali semua" teori ZFC. Dalam video ini, pada akhirnya dikatakan dengan sangat indah tentang kekuatan yang tidak dapat dicapai, tetapi kita harus melanjutkan.

Lebih jauh lagi.


Tentu saja, kita bisa melangkah lebih jauh dengan iterasi $ powerset (\ theta) $ . Setelah melalui semua langkah yang dijelaskan di atas, membangun menara repeater besar, kita kembali bertemu dengan kardinal yang tidak dapat dicapai (tapi sekarang kita tidak memerlukan aksioma baru, dengan aksioma tentang keberadaan kekuatan yang tidak dapat dicapai yang baru saja kita tambahkan, ini telah dapat dibuktikan). Dan lagi dan lagi.

$ \ theta_0 \ rightarrow \ theta_1 \ rightarrow \ theta_2 \ rightarrow ... \ rightarrow \ theta_ {36463634} \ rightarrow $

Perhatikan bahwa sekarang panah tidak masuk akal bagi kami seperti menjalankan fungsi Powerset (), tetapi GetNextInaccessible (). Kalau tidak, semuanya terlihat sangat mirip, kami memiliki:

$ \ theta _ {\ theta_1} \ rightarrow \ theta _ {\ theta_2} ... \ rightarrow \ theta _ {\ theta_ \ omega} \ rightarrow \ theta _ {\ theta_ \ theta} \ rightarrow $



Nah, sekarang kita pasti akan mencapai sesuatu ... Atau tidak?

Hierarki dengan kapasitas besar.


Ya, dengan GetNextInaccessible kami mengalami kekuatan yang sangat sulit dicapai. Keberadaannya membutuhkan satu aksioma lagi. Ada kekuatan hyper-hyper-unreachable. Dan sebagainya. Tetapi ada cara lain untuk menentukan kekuatan , tidak hanya melalui pencapaian yang tidak terjangkau:



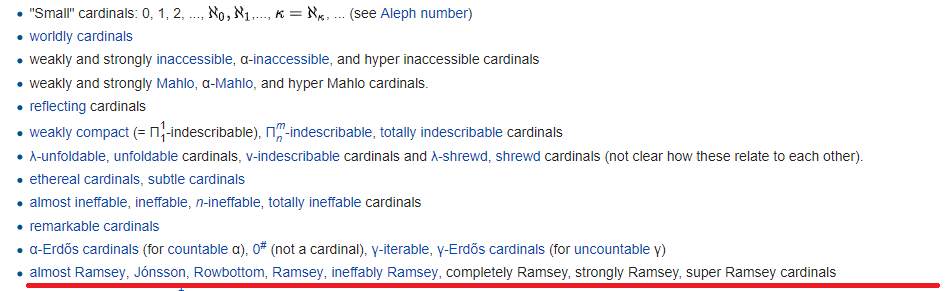
Di balik setiap tautan, sebagai suatu peraturan, seluruh hierarki tanpa akhir dengan sejumlah awalan hiper dan repeater. Namun, jumlah total formula yang menentukan kardinal yang tidak dapat dicapai tidak sebesar itu - karena jumlah formula dapat dihitung !!! Karena itu, cepat atau lambat mereka akan berakhir. Di mana mereka berakhir, garis merah ditarik. Segala sesuatu di bawah garis ini didefinisikan lebih goyah, meskipun secara formal.

Garis merah itu sendiri menandai akhir dari alam semesta Gödel (tapi jangan lupa bahwa Gödel menciptakan DUA alam semesta yang berbeda) - alam semesta set yang dibangun dari bawah menggunakan formula. Kapasitas di atas garis merah disebut hmm, "kecil", dan di bawah - besar:



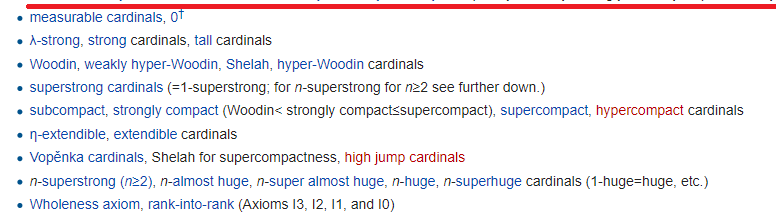
Gagasan utama di dalamnya adalah bahwa alam semesta himpunan menjadi begitu besar sehingga mulai terulang kembali dalam pengertian yang berbeda. Setiap baris, seperti biasa, memerlukan aksioma terpisah, dan beberapa. Dan yang lebih menarik, semua ini tidak berguna seperti yang Anda kira. Misalnya, aksioma terkuat (peringkat-ke-peringkat), di garis paling bawah, diperlukan untuk membuktikan fakta tentang tablet .

Di bawah ini adalah survei, pilihan terakhir didekripsi di sini .

Source: https://habr.com/ru/post/id445904/

More articles:


All Articles