Struktur Data Eksotis: Modifikasi Merkle Patricia Trie

"Setan macam apa yang harus kuingat dengan hafal semua algoritma dan struktur data sialan ini?"

Tentang ini bermuara pada komentar dari sebagian besar artikel tentang perjalanan wawancara teknis. Tesis utama, sebagai suatu peraturan, adalah bahwa segala sesuatu yang digunakan dengan satu atau lain cara telah dilaksanakan sepuluh kali dan sangat tidak mungkin bahwa programmer biasa harus berurusan dengan. Ya, sampai taraf tertentu ini benar. Tetapi, ternyata, tidak semuanya dilaksanakan, dan saya, sayangnya (atau untungnya?) Masih harus membuat Struktur Data.

Merkle Patricia Trie Yang Dimodifikasi Secara Misterius.

Karena tidak ada informasi tentang pohon ini sama sekali tentang habr, dan pada medium - sedikit lagi, saya ingin memberi tahu Anda jenis hewan apa itu dan dengan apa ia dimakan.

Apa ini

Penafian: sumber utama informasi untuk implementasi bagi saya adalah kertas Kuning , serta kode sumber parity-ethereum dan go-ethereum . Ada sedikit informasi teoretis tentang pembenaran keputusan tertentu, jadi semua kesimpulan tentang alasan pengambilan keputusan tertentu adalah milik saya. Jika saya salah dalam sesuatu - saya akan senang untuk koreksi di komentar.

Pohon adalah struktur data yang merupakan grafik asiklik yang terhubung. Semuanya sederhana di sini, semua orang akrab dengan ini.

Pohon awalan adalah pohon akar di mana pasangan kunci-nilai dapat disimpan karena fakta bahwa node dibagi menjadi dua jenis: yang berisi bagian dari jalur (awalan), dan simpul daun yang berisi nilai yang disimpan. Nilai ada di pohon jika dan hanya jika, menggunakan kunci, kita bisa pergi jauh-jauh dari akar pohon dan menemukan sebuah simpul dengan nilai di akhir.

Pohon PATRICIA adalah pohon awalan di mana awalannya adalah biner - yaitu, setiap simpul kunci menyimpan informasi tentang satu bit.

Pohon Merkle adalah pohon hash yang dibangun di atas semacam rantai data, yang menggabungkan hash yang sama ini menjadi satu (root), menyimpan informasi tentang keadaan semua blok data. Artinya, hash root adalah semacam "tanda tangan digital" dari keadaan rantai blok. Hal ini digunakan secara aktif di blockchain, dan lebih lanjut tentang hal ini dapat ditemukan di sini .

Total: Merkle Patricia Trie yang Dimodifikasi (selanjutnya disingkat MPT) adalah pohon hash yang menyimpan pasangan nilai kunci, dan kunci-kunci tersebut disajikan dalam bentuk biner. Dan apa sebenarnya "Dimodifikasi" tentang, kita akan mencari tahu nanti ketika kita membahas implementasi.

Kenapa ini?

MPT digunakan dalam proyek Ethereum untuk menyimpan data tentang akun, transaksi, hasil eksekusi dan data lain yang diperlukan untuk berfungsinya sistem.
Tidak seperti Bitcoin, di mana statusnya implisit dan dihitung oleh setiap node secara independen, saldo setiap akun (serta data yang terkait dengannya) disimpan langsung di blockchain di udara. Selain itu, lokasi dan kekekalan data harus disediakan secara kriptografis - beberapa orang akan menggunakan mata uang kripto di mana saldo akun acak dapat berubah tanpa alasan obyektif.

Masalah utama yang dihadapi oleh pengembang Ethereum adalah penciptaan struktur data yang secara efektif dapat menyimpan pasangan nilai kunci dan pada saat yang sama memberikan verifikasi data yang disimpan. Jadi MPT muncul.

Bagaimana itu?

MPT adalah pohon PATRICIA awalan di mana kunci adalah urutan byte.

Tepi di pohon ini adalah urutan gigitan (setengah byte). Dengan demikian, satu simpul dapat memiliki hingga enam belas keturunan (sesuai dengan cabang dari 0x0 hingga 0xF).

Node dibagi menjadi 3 jenis:

• Simpul cabang. Node yang digunakan untuk bercabang. Berisi hingga 1 hingga 16 tautan ke simpul anak. Mungkin juga mengandung nilai.
• Simpul ekstensi. Node bantu yang menyimpan beberapa bagian dari jalur yang umum untuk beberapa simpul anak, serta tautan ke simpul cabang, yang terletak di bawah.
• Simpul daun. Node yang berisi bagian dari jalur dan nilai yang disimpan. Itu adalah akhir dari rantai.

Seperti yang telah disebutkan, MPT dibangun di atas repositori kv lain, yang menyimpan node dalam bentuk "link" => " RLP encoded node".

Dan di sini kita datang dengan konsep baru: RLP. Singkatnya, ini adalah metode pengkodean data yang mewakili urutan daftar atau byte. Contoh: [ "cat", "dog" ] = [ 0xc8, 0x83, 'c', 'a', 't', 0x83, 'd', 'o', 'g' ] . Saya tidak akan membahas secara rinci, dan dalam implementasi saya menggunakan perpustakaan yang sudah jadi, karena cakupan topik ini juga akan mengembang artikel yang sudah agak besar. Jika Anda masih tertarik, Anda dapat membaca lebih lanjut di sini . Kami membatasi diri pada fakta bahwa kami dapat menyandikan data dalam RLP dan men-dekode kembali.

Tautan ke sebuah simpul didefinisikan sebagai berikut: jika panjang simpul yang dikodekan RLP adalah 32 atau lebih byte, maka tautan tersebut adalah keccak dari representasi RLP dari simpul tersebut. Jika panjangnya kurang dari 32 byte, maka tautannya adalah representasi RLP dari simpul itu sendiri.

Jelas, dalam kasus kedua, Anda tidak perlu menyimpan node ke database, karena itu akan disimpan sepenuhnya di dalam simpul induk.

Kombinasi tiga jenis node memungkinkan Anda untuk secara efektif menyimpan data dalam kasus ketika ada beberapa kunci (maka sebagian besar jalur akan disimpan dalam ekstensi dan simpul daun, dan akan ada beberapa simpul cabang), dan dalam kasus ketika ada banyak node (jalur tidak akan disimpan secara eksplisit, tetapi mereka akan "mengumpulkan" selama bagian melalui node cabang).

Contoh lengkap pohon menggunakan semua jenis node:

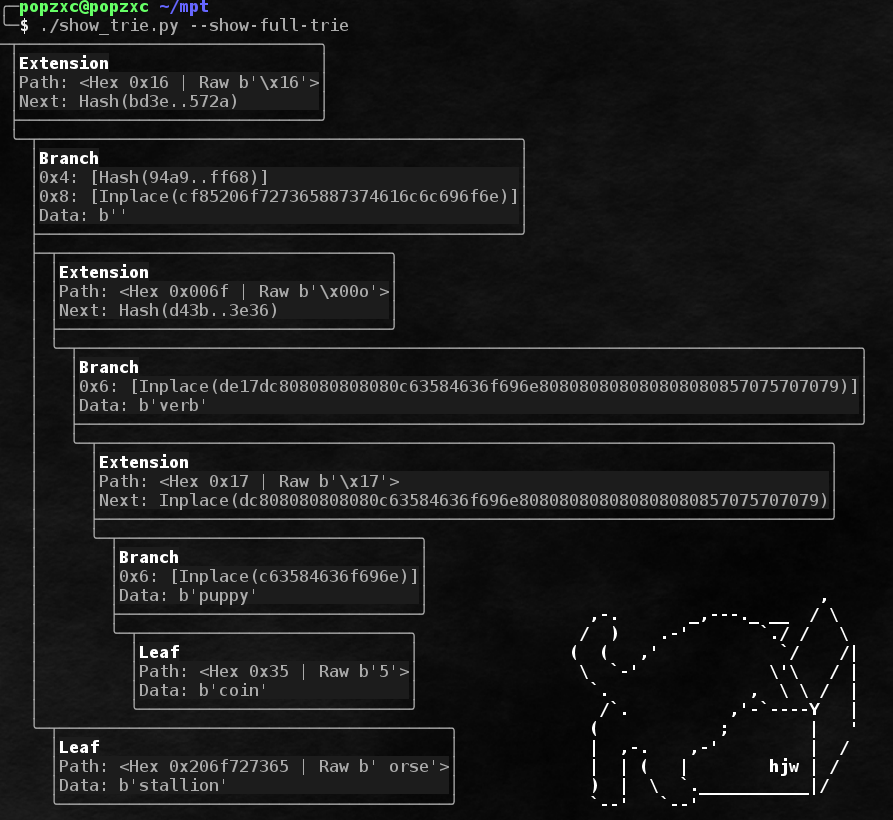
Seperti yang mungkin Anda perhatikan, bagian jalur yang disimpan memiliki awalan. Diperlukan awalan untuk beberapa tujuan:

1. Untuk membedakan node ekstensi dari node daun.
2. Untuk menyelaraskan urutan jumlah aneh camilan.

Aturan untuk membuat awalan sangat sederhana:

• Awalan membutuhkan 1 nibble. Jika panjang jalur (tidak termasuk awalan) ganjil, maka jalur dimulai segera setelah awalan. Jika panjang lintasan genap, untuk menyelaraskan setelah awalan, nibble 0x0 ditambahkan terlebih dahulu.
• Awalan awalnya 0x0.
• Jika panjang jalurnya ganjil, maka 0x1 ditambahkan ke awalan, jika genap - 0x0.
• Jika jalur mengarah ke simpul daun, maka 0x2 ditambahkan ke awalan, jika 0x0 ditambahkan ke simpul ekstensi.

Pada beatiks, saya pikir, akan lebih jelas:

 0b0000 =>  , Extension  0b0001 =>  , Extension  0b0010 =>  , Leaf  0b0011 =>  , Leaf  

Penghapusan itu bukan penghapusan

Terlepas dari kenyataan bahwa pohon memiliki operasi menghapus node, pada kenyataannya, semua yang pernah ditambahkan tetap berada di pohon selamanya.

Ini diperlukan agar tidak membuat pohon lengkap untuk setiap blok, tetapi hanya menyimpan perbedaan antara versi pohon yang lama dan yang baru.

Oleh karena itu, dengan menggunakan hash root yang berbeda sebagai titik masuk, kita bisa mendapatkan salah satu dari keadaan di mana pohon itu berada.

Ini tidak semua optimasi. Ada lebih banyak, tetapi kami tidak akan membicarakannya - dan artikelnya besar. Namun, Anda bisa membaca sendiri.

Implementasi

Teorinya sudah berakhir, mari kita beralih ke praktik. Kami akan menggunakan lingua franca dari dunia IT, yaitu python .

Karena akan ada banyak kode, dan untuk format artikel, banyak yang harus dikurangi dan dibagi, saya akan segera meninggalkan tautan ke github .
Jika perlu, di sana Anda dapat melihat seluruh gambar.

Pertama, kita mendefinisikan antarmuka pohon yang ingin kita dapatkan sebagai hasilnya:

 class MerklePatriciaTrie: def __init__(self, storage, root=None): pass def root(self): pass def get(self, encoded_key): pass def update(self, encoded_key, encoded_value): pass def delete(self, encoded_key): pass 

Antarmukanya sangat sederhana. Operasi yang tersedia adalah mendapatkan, menghapus, memasukkan dan mengubah (digabung dalam pembaruan), serta mendapatkan hash root.

Penyimpanan akan ditransfer ke metode __init__ - struktur data seperti dict di mana kita akan menyimpan node, serta root - "atas" pohon. Jika None yang dilewatkan sebagai root , kami menganggap bahwa pohon itu kosong dan bekerja dari awal.

_Remark: Anda mungkin bertanya-tanya mengapa variabel dalam metode ini dinamai encoded_key dan encoded_value , dan bukan hanya key / value . Jawabannya sederhana: sesuai dengan spesifikasi, semua kunci dan nilai harus dikodekan dalam RLP . Kami tidak akan menyusahkan diri dengan hal ini dan meninggalkan pekerjaan ini di pundak pengguna perpustakaan._

Namun, sebelum kita mulai menerapkan pohon itu sendiri, dua hal penting harus dilakukan:

1. Menerapkan kelas NibblePath , yang merupakan rantai nibbles, agar tidak menyandikannya secara manual.
2. Untuk mengimplementasikan kelas Node dalam kerangka kerja kelas ini - Extension , Leaf dan Branch .

Nibblepath

Jadi, NibblePath . Karena kita akan secara aktif bergerak di sekitar pohon, dasar dari fungsi kelas kita haruslah kemampuan untuk mengatur "offset" dari awal jalan, serta menerima menggigit tertentu. Mengetahui hal ini, kami mendefinisikan dasar kelas kami (serta beberapa konstanta yang berguna untuk bekerja dengan awalan di bawah):

 class NibblePath: ODD_FLAG = 0x10 LEAF_FLAG = 0x20 def __init__(self, data, offset=0): self._data = data # ,   . self._offset = offset #      def consume(self, amount): # "" N      . self._offset += amount return self def at(self, idx): #      idx = idx + self._offset #    ,   ,    , #   ,    -      . byte_idx = idx // 2 nibble_idx = idx % 2 #   . byte = self._data[byte_idx] #      . nibble = byte >> 4 if nibble_idx == 0 else byte & 0x0F return nibble 

Cukup sederhana, bukan?

Masih menulis fungsi hanya untuk encoding dan decoding urutan camilan.

 class NibblePath: # ... def decode_with_type(data): #   : # ,     ,    . is_odd_len = data[0] & NibblePath.ODD_FLAG == NibblePath.ODD_FLAG is_leaf = data[0] & NibblePath.LEAF_FLAG == NibblePath.LEAF_FLAG #    ,     #    . offset  , #       "" . offset = 1 if is_odd_len else 2 return NibblePath(data, offset), is_leaf def encode(self, is_leaf): output = [] #    ,       . nibbles_len = len(self._data) * 2 - self._offset is_odd = nibbles_len % 2 == 1 #  . prefix = 0x00 #    ,    . #      (self.at(0))     . #           (0x0). prefix += self.ODD_FLAG + self.at(0) if is_odd else 0x00 #  ,  Leaf node,  . prefix += self.LEAF_FLAG if is_leaf else 0x00 output.append(prefix) # ,      ,  . pos = nibbles_len % 2 #          , #     2 ,    , #     , #    . while pos < nibbles_len: byte = self.at(pos) * 16 + self.at(pos + 1) output.append(byte) pos += 2 return bytes(output) 

Pada prinsipnya, ini adalah minimum yang diperlukan untuk pekerjaan yang nyaman dengan camilan. Tentu saja, dalam implementasi saat ini ada sejumlah metode tambahan (seperti combine , menggabungkan dua jalur menjadi satu), tetapi implementasinya sangat sepele. Jika tertarik, versi lengkapnya dapat ditemukan di sini .

Node

Seperti yang sudah kita ketahui, node kita dibagi menjadi tiga jenis: Leaf, Extension dan Branch. Semuanya dapat dikodekan dan didekodekan, dan satu-satunya perbedaan adalah data yang disimpan di dalamnya. Sejujurnya, ini adalah tipe data aljabar yang diminta, dan di Rust , misalnya, saya akan menulis sesuatu dengan semangat:

 pub enum Node<'a> { Leaf(NibblesSlice<'a>, &'a [u8]), Extension(NibblesSlice<'a>, NodeReference), Branch([Option<NodeReference>; 16], Option<&'a [u8]>), } 

Namun, tidak ada ADT dalam python seperti itu, jadi kami akan mendefinisikan kelas Node , dan di dalamnya ada tiga kelas yang sesuai dengan jenis simpul. Kami menerapkan pengkodean langsung di kelas node, dan decoding di kelas Node .

Implementasinya, bagaimanapun, adalah dasar:

Daun:

 class Leaf: def __init__(self, path, data): self.path = path self.data = data def encode(self): #    --    , #   -  ,   -  . return rlp.encode([self.path.encode(True), self.data]) 

Ekstensi:

 class Extension: def __init__(self, path, next_ref): self.path = path self.next_ref = next_ref def encode(self): #    --    , #   -  ,   -    . next_ref = _prepare_reference_for_encoding(self.next_ref) return rlp.encode([self.path.encode(False), next_ref]) 

Cabang:

 class Branch: def __init__(self, branches, data=None): self.branches = branches self.data = data def encode(self): #    --    ,  #  16 -     (  ), #   -   (  ). branches = list(map(_prepare_reference_for_encoding, self.branches)) return rlp.encode(branches + [self.data]) 

Semuanya sangat sederhana. Satu-satunya hal yang dapat menimbulkan pertanyaan adalah fungsi _prepare_reference_for_encoding .

Kemudian saya akui, saya harus menggunakan tongkat kecil. Faktanya adalah bahwa pustaka rlp mendekode data secara rekursif, dan tautan ke simpul lain, seperti yang kita ketahui, dapat berupa data rlp (jika simpul yang disandikan kurang dari 32 karakter). Bekerja dengan tautan dalam dua format - byte hash dan simpul yang didekodekan - sangat merepotkan. Oleh karena itu, saya menulis dua fungsi yang, setelah mendekode simpul, mengembalikan tautan dalam format byte, dan menerjemahkannya jika perlu, sebelum menyimpan. Fungsi-fungsi ini adalah:

 def _prepare_reference_for_encoding(ref): #    ( ,   ) --  . #       :) if 0 < len(ref) < 32: return rlp.decode(ref) return ref def _prepare_reference_for_usage(ref): #     -   . #          . if isinstance(ref, list): return rlp.encode(ref) return ref 

Akhiri dengan node dengan menulis kelas Node . Hanya akan ada 2 metode di dalamnya: decode simpul dan ubah simpul menjadi tautan.

 class Node: # class Leaf(...) # class Extension(...) # class Branch(...) def decode(encoded_data): data = rlp.decode(encoded_data) # 17  -  Branch . if len(data) == 17: branches = list(map(_prepare_reference_for_usage, data[:16])) node_data = data[16] return Node.Branch(branches, node_data) #    17,   2.   - . #      ,     . path, is_leaf = NibblePath.decode_with_type(data[0]) if is_leaf: return Node.Leaf(path, data[1]) else: ref = _prepare_reference_for_usage(data[1]) return Node.Extension(path, ref) def into_reference(node): #    . #      32 , #   -   . #       . encoded_node = node.encode() if len(encoded_node) < 32: return encoded_node else: return keccak_hash(encoded_node) 

Istirahat

Fuh! Ada banyak informasi. Saya pikir sudah waktunya untuk bersantai. Ini kucing lain untuk Anda:

Milota, kan? Oke, kembali ke pohon kita.

MerklePatriciaTrie

Hore - elemen tambahan siap, kami sampaikan yang paling lezat. Untuk jaga-jaga, saya akan mengingatkan antarmuka pohon kami. Pada saat yang sama, kami menerapkan metode __init__ .

 class MerklePatriciaTrie: def __init__(self, storage, root=None): self._storage = storage self._root = root def root(self): pass def get(self, encoded_key): pass def update(self, encoded_key, encoded_value): pass def delete(self, encoded_key): pass 

Tetapi dengan metode yang tersisa kita akan berurusan satu per satu.

dapatkan

Metode get (seperti, pada prinsipnya, metode lain) akan terdiri dari dua bagian. Metode itu sendiri akan menyiapkan data dan membawa hasilnya ke bentuk yang diharapkan, sementara pekerjaan nyata akan terjadi di dalam metode tambahan.

Metode dasar sangat sederhana:

 class MerklePatriciaTrie: # ... def get(self, encoded_key): if not self._root: raise KeyError path = NibblePath(encoded_key) #       #  ,    ,    . result_node = self._get(self._root, path) if type(result_node) is Node.Extension or len(result_node.data) == 0: raise KeyError return result_node.data 

Namun, _get tidak jauh lebih rumit: untuk mencapai node yang diinginkan, kita perlu beralih dari root ke seluruh path yang disediakan. Jika pada akhirnya kami menemukan sebuah simpul dengan data (Daun atau Cabang) - hore, data diterima. Jika tidak memungkinkan untuk lulus, maka kunci yang diperlukan tidak ada di pohon.

Implementasi:

 class MerklePatriciaTrie: # ... def _get(self, node_ref, path): #      . node = self._get_node(node_ref) #    --   . #   ,      . if len(path) == 0: return node if type(node) is Node.Leaf: #     Leaf-,     , #      . if node.path == path: return node elif type(node) is Node.Extension: #    -- Extension,    . if path.starts_with(node.path): rest_path = path.consume(len(node.path)) return self._get(node.next_ref, rest_path) elif type(node) is Node.Branch: #    -- Branch,     . #   ,           #  :      . branch = node.branches[path.at(0)] if len(branch) > 0: return self._get(branch, path.consume(1)) #    ,        , #     . raise KeyError 

Nah, pada saat yang sama, kami akan menulis metode untuk menyimpan dan memuat node. Mereka sederhana:

 class MerklePatriciaTrie: # ... def _get_node(self, node_ref): raw_node = None if len(node_ref) == 32: raw_node = self._storage[node_ref] else: raw_node = node_ref return Node.decode(raw_node) def _store_node(self, node): reference = Node.into_reference(node) if len(reference) == 32: self._storage[reference] = node.encode() return reference 

pembaruan

Metode update sudah lebih menarik. Langsung saja sampai akhir dan masukkan node Leaf tidak akan selalu berhasil. Kemungkinan titik pemisahan kunci akan berada di suatu tempat di dalam simpul Leaf atau Extension yang sudah disimpan. Dalam hal ini, Anda harus memisahkannya dan membuat beberapa node baru.

Secara umum, semua logika dapat dijelaskan dengan aturan berikut:

1. Sementara path sepenuhnya bertepatan dengan node yang ada, kami secara rekursif turun pohon.
2. Jika jalur selesai dan kami berada di simpul Cabang atau Daun, itu berarti update hanya memperbarui nilai yang sesuai dengan kunci ini.
3. Jika jalur dibagi (artinya, kami tidak memperbarui nilai, tetapi menyisipkan yang baru), dan kami berada di simpul Cabang - membuat simpul Daun dan menentukan tautan ke sana di cabang cabang cabang yang sesuai.
4. Jika jalur dibagi dan kita berada di simpul Leaf atau Extension, kita perlu membuat simpul Cabang yang memisahkan jalur, dan, jika perlu, simpul Ekstensi untuk bagian umum dari jalur.

Mari secara bertahap ungkapkan ini dalam kode. Kenapa bertahap? Karena metodenya besar dan akan sulit untuk memahaminya secara massal.
Namun, saya akan meninggalkan tautan ke metode lengkap di sini .

 class MerklePatriciaTrie: # ... def update(self, encoded_key, encoded_value): path = NibblePath(encoded_key) result = self._update(self._root, path, encoded_value) self._root = result def _update(self, node_ref, path, value): #       (,   ), #       . if not node_ref: return self._store_node(Node.Leaf(path, value)) #          #    . node = self._get_node(node_ref) if type(node) == Node.Leaf: ... elif type(node) == Node.Extension: ... elif type(node) == Node.Branch: ... 

Tidak ada cukup logika umum, semua yang paling menarik adalah di dalam if s.

if type(node) == Node.Leaf

Pertama, mari kita berurusan dengan Leaf node. Hanya 2 skenario yang memungkinkan untuk itu:

1. Sisa lintasan yang kita ikuti persis sama dengan lintasan yang disimpan dalam simpul Daun. Dalam hal ini, kita hanya perlu mengubah nilainya, menyimpan simpul baru dan mengembalikan tautan ke sana.

   
   

2. Jalannya berbeda.
   Dalam hal ini, Anda perlu membuat simpul Cabang yang memisahkan dua jalur.
   Jika salah satu path kosong, maka nilainya akan ditransfer langsung ke simpul-cabang.
   Jika tidak, kita harus membuat dua node Leaf yang dipersingkat oleh panjang bagian umum dari path + 1 nibble (nibble ini akan ditunjukkan oleh indeks cabang yang sesuai dari node Branch).

   
   

Anda juga perlu memeriksa apakah ada bagian umum dari jalur untuk memahami apakah kita perlu membuat simpul ekstensi juga.

Dalam kode tersebut, akan terlihat seperti ini:

 if type(node) == Node.Leaf: if node.path == path: #  .       . node.data = value return self._store_node(node) #    . #    . common_prefix = path.common_prefix(node.path) #      . path.consume(len(common_prefix)) node.path.consume(len(common_prefix)) #  Branch . branch_reference = self._create_branch_node(path, value, node.path, node.data) # ,    Extension-. if len(common_prefix) != 0: return self._store_node(Node.Extension(common_prefix, branch_reference)) else: return branch_reference 

Prosedur _create_branch_node adalah sebagai berikut:

 def _create_branch_node(self, path_a, value_a, path_b, value_b): #    Branch-. branches = [b''] * 16 # ,     Branch- . branch_value = b'' if len(path_a) == 0: branch_value = value_a elif len(path_b) == 0: branch_value = value_b #    Leaf-,  . self._create_branch_leaf(path_a, value_a, branches) self._create_branch_leaf(path_b, value_b, branches) #  Branch-     . return self._store_node(Node.Branch(branches, branch_value)) def _create_branch_leaf(self, path, value, branches): # ,     Leaf-. if len(path) > 0: #    ( ). idx = path.at(0) #  Leaf-   ,     . leaf_ref = self._store_node(Node.Leaf(path.consume(1), value)) branches[idx] = leaf_ref 

if type(node) == Node.Extension

Dalam kasus simpul ekstensi, semuanya tampak seperti simpul daun.

1. Jika jalur dari simpul Ekstensi adalah awalan untuk jalur kami, kami cukup beralih secara rekursif.

   
   

2. Kalau tidak, kita perlu melakukan pemisahan menggunakan simpul Cabang, seperti dalam kasus yang dijelaskan di atas.

   
   

Dengan demikian, kodenya:

 elif type(node) == Node.Extension: if path.starts_with(node.path): #         . new_reference = \ self._update(node.next_ref, path.consume(len(node.path)), value) return self._store_node(Node.Extension(node.path, new_reference)) #  Extension-. #     . common_prefix = path.common_prefix(node.path) #  . path.consume(len(common_prefix)) node.path.consume(len(common_prefix)) #  Branch- ,  ,    . branches = [b''] * 16 branch_value = value if len(path) == 0 else b'' #     Leaf-  Extension- . self._create_branch_leaf(path, value, branches) self._create_branch_extension(node.path, node.next_ref, branches) branch_reference = self._store_node(Node.Branch(branches, branch_value)) # ,    Extension-. if len(common_prefix) != 0: return self._store_node(Node.Extension(common_prefix, branch_reference)) else: return branch_reference 

Prosedur _create_branch_extension secara logis setara dengan prosedur _create_branch_leaf , tetapi bekerja dengan node Extension.

if type(node) == Node.Branch

Tetapi dengan simpul Cabang, semuanya sederhana. Jika path kosong, kami cukup menyimpan nilai baru di simpul Cabang saat ini. Jika jalan tidak kosong, kita “gigit” satu gigitan dari sana dan secara rekursif turun lebih rendah.

Kode, saya pikir, tidak perlu komentar.

 elif type(node) == Node.Branch: if len(path) == 0: return self._store_node(Node.Branch(node.branches, value)) idx = path.at(0) new_reference = self._update(node.branches[idx], path.consume(1), value) node.branches[idx] = new_reference return self._store_node(node) 

hapus

Fuh! Metode terakhir tetap. Dia yang paling ceria. Kompleksitas dari penghapusan adalah bahwa kita perlu mengembalikan struktur ke keadaan seperti seharusnya jika kita telah melakukan seluruh rantai update , kecuali hanya kunci yang dihapus.

, , , , . "", , .

. , N- , N+1 . enum — DeleteAction , .

delete :

 class MerklePatriciaTrie: # ... # Enum, ,         . class _DeleteAction(Enum): #    . #     , #        (_DeleteAction, None). DELETED = 1, #    (,    ). #     ,    #    : (_DeleteAction, ___). UPDATED = 2, #    Branch-  .   -- #    : # (_DeleteAction, (___, ___)) USELESS_BRANCH = 3 def delete(self, encoded_key): if self._root is None: return path = NibblePath(encoded_key) action, info = self._delete(self._root, path) if action == MerklePatriciaTrie._DeleteAction.DELETED: #   . self._root = None elif action == MerklePatriciaTrie._DeleteAction.UPDATED: #   . new_root = info self._root = new_root elif action == MerklePatriciaTrie._DeleteAction.USELESS_BRANCH: #   . _, new_root = info self._root = new_root def _delete(self, node_ref, path): node = self._get_node(node_ref) if type(node) == Node.Leaf: pass elif type(node) == Node.Extension: pass elif type(node) == Node.Branch: pass 

, get update . . .

if type(node) == Node.Leaf

. . — , , .

:

 if type(node) == Node.Leaf: if path == node.path: return MerklePatriciaTrie._DeleteAction.DELETED, None else: raise KeyError 

, "" — . , . .

if type(node) == Node.Extension

C Extension- :

1. , Extension- . — .
2. _delete , "" .
3. . :

• . .
• . .
• Branch-. . , Branch- . , , Leaf-. — Extension-.

:

 elif type(node) == Node.Extension: if not path.starts_with(node.path): raise KeyError #   . #       . action, info = self._delete(node.next_ref, path.consume(len(node.path))) if action == MerklePatriciaTrie._DeleteAction.DELETED: return action, None elif action == MerklePatriciaTrie._DeleteAction.UPDATED: #    ,     . child_ref = info new_ref = self._store_node(Node.Extension(node.path, child_ref)) return action, new_ref elif action == MerklePatriciaTrie._DeleteAction.USELESS_BRANCH: #     Branch-. stored_path, stored_ref = info # ,     Branch-. child = self._get_node(stored_ref) new_node = None if type(child) == Node.Leaf: #  branch-  . #     Leaf-  Extension. path = NibblePath.combine(node.path, child.path) new_node = Node.Leaf(path, child.data) elif type(child) == Node.Extension: #  Branch-  Extension-. #       . path = NibblePath.combine(node.path, child.path) new_node = Node.Extension(path, child.next_ref) elif type(child) == Node.Branch: #  Branch-      Branch-. #    Extension-    . path = NibblePath.combine(node.path, stored_path) new_node = Node.Extension(path, stored_ref) new_reference = self._store_node(new_node) return MerklePatriciaTrie._DeleteAction.UPDATED, new_reference 

if type(node) == Node.Branch

.

, . Branch-, …

Mengapa Branch- Leaf- ( ) Extension- ( ).
, . , — Leaf-. — Extension-. , , 2 — Branch- .

? :

:

1. , .
2. , _delete .

:

 elif type(node) == Node.Branch: action = None idx = None info = None if len(path) == 0 and len(node.data) == 0: raise KeyError elif len(path) == 0 and len(node.data) != 0: node.data = b'' action = MerklePatriciaTrie._DeleteAction.DELETED else: #   ,    . #    . idx = path.at(0) if len(node.branches[idx]) == 0: raise KeyError action, info = self._delete(node.branches[idx], path.consume(1)) #  ,   ,  . #      -    #    . node.branches[idx] = b'' 

_DeleteAction .

1. Branch- , ( , ). .

 if action == MerklePatriciaTrie._DeleteAction.UPDATED: #   . next_ref = info node.branches[idx] = next_ref reference = self._store_node(node) return MerklePatriciaTrie._DeleteAction.UPDATED, reference elif action == MerklePatriciaTrie._DeleteAction.USELESS_BRANCH: #    . _, next_ref = info node.branches[idx] = next_ref reference = self._store_node(node) return MerklePatriciaTrie._DeleteAction.UPDATED, reference 

1. ( , ), , .

. :

• . , , , . , .
• , . Leaf- . .
• , . , , .
• , , Branch- . , _DeleteAction — UPDATED .

 if action == MerklePatriciaTrie._DeleteAction.DELETED: non_empty_count = sum(map(lambda x: 1 if len(x) > 0 else 0, node.branches)) if non_empty_count == 0 and len(node.data) == 0: # Branch- ,  . return MerklePatriciaTrie._DeleteAction.DELETED, None elif non_empty_count == 0 and len(node.data) != 0: #  ,   . path = NibblePath([]) reference = self._store_node(Node.Leaf(path, node.data)) return MerklePatriciaTrie._DeleteAction.USELESS_BRANCH, (path, reference) elif non_empty_count == 1 and len(node.data) == 0: #  ,   . return self._build_new_node_from_last_branch(node.branches) else: #  1+   ,  2+ . # Branch-  ,   - UPDATED. reference = self._store_node(node) return MerklePatriciaTrie._DeleteAction.UPDATED, reference 

_build_new_node_from_last_branch .

— Leaf Extension, , .

— Branch, Extension , , Branch.

 def _build_new_node_from_last_branch(self, branches): #    . idx = 0 for i in range(len(branches)): if len(branches[i]) > 0: idx = i break #     . prefix_nibble = NibblePath([idx], offset=1) #     child = self._get_node(branches[idx]) path = None node = None #   . if type(child) == Node.Leaf: path = NibblePath.combine(prefix_nibble, child.path) node = Node.Leaf(path, child.data) elif type(child) == Node.Extension: path = NibblePath.combine(prefix_nibble, child.path) node = Node.Extension(path, child.next_ref) elif type(child) == Node.Branch: path = prefix_nibble node = Node.Extension(path, branches[idx]) #  . reference = self._store_node(node) return MerklePatriciaTrie._DeleteAction.USELESS_BRANCH, (path, reference) 

Sisanya

. , … root .

Di sini:

 class MerklePatriciaTrie: # ... def root(self): return self._root 

, .

… . , , Ethereum . , , , . , :)

, , pip install -U eth_mpt — .

Hasil

?

, -, , - , , . — , .

-, , , — . , skip list interval tree, — , , .

-, , . , - .

-, — .

, , — !

: 1 , 2 , 3 . ! , .