💦 ⏱️ 👩🏼‍🚀 Kami memodelkan algoritma MUSIK untuk menentukan arah kedatangan gelombang elektromagnetik 👨‍👨‍👧‍👧 〰️ 🌽

aaspcats

Kata Pengantar

Saya akan mulai perkenalan saya dari jauh. Sekali waktu, di kejauhan 2016-2017, hambamu yang rendah hati berhasil mengikuti kursus pelatihan enam bulan ke kota jauh Ilmenau (Jerman), di mana ia berhasil (pada umumnya) menyelesaikan program master Komunikasi dan pemrosesan sinyal . Program itu tidak mudah, tetapi sekarang bahkan menyenangkan untuk mengingatnya. Terkadang ...

Jadi, di akhir pelatihan ini, selain ijazah, saya masih memiliki beberapa materi yang berbeda di tangan saya, yang saya pikir salah untuk tidak dibagikan.

Salah satu bahan ini ada di depan Anda.

Apa tujuan yang saya kejar saat mempersiapkan seminar :

berbicara tentang beberapa pendekatan "pintar" yang sudah mapan dalam topik susunan antena yang paling mudah diakses dan melakukannya dalam bahasa Rusia;
melakukan simulasi kecil dengan Python 3 untuk menggerakkan sesama insinyur radio untuk melihat lebih dekat bahasa pemrograman (jika Anda belum melihat dari dekat);
menyediakan tautan ke literatur berbahasa Inggris yang baik - tanpa membaca sumber asing, sekarang, sayangnya, tidak ada tempat.

Apa yang harus dipertimbangkan :

Metode MUSIK (Klasifikasi Sebagian Besar) - ini, pada kenyataannya, mengacu pada pratinjau.

Contoh pembentukan bagan dan metode MVDR dapat ditemukan di sini (jika ada pertanyaan atau saran untuk bahan tambahan, diskusi dapat dilanjutkan di Github.Gist).

Seperti yang saya katakan di atas, kita akan menggunakan Python, yaitu:

import numpy as np import matplotlib.pyplot as plt

Mengapa tidak MATLAB, salah satu kandidat paling populer dan nyaman untuk pemodelan aljabar linier, Anda bertanya? Karena, saya ingin menunjukkan bahwa pekerjaan serupa dapat dilakukan dengan Python, dan cakupan Python jauh lebih luas daripada MATLAB. Oleh karena itu, mengenal sintaksis Python adalah hal yang berguna, menurut saya.

Ayo mulai!

Rumus disiapkan melalui https://upmath.me/ . Terima kasih kepada pencipta untuk alat yang hebat!

Pernyataan masalah

Misalkan ada array antena linier yang terdiri dari sejumlah elemen yang terpisah satu sama lain $\ Delta = \ frac {\ lambda} {2}$ (langkah array antena), di mana $\ lambda$ - panjang gelombang pembawa elektromagnetik (EM).

Gelombang elektromagnetik jatuh pada susunan antena ini dari arah yang berbeda.

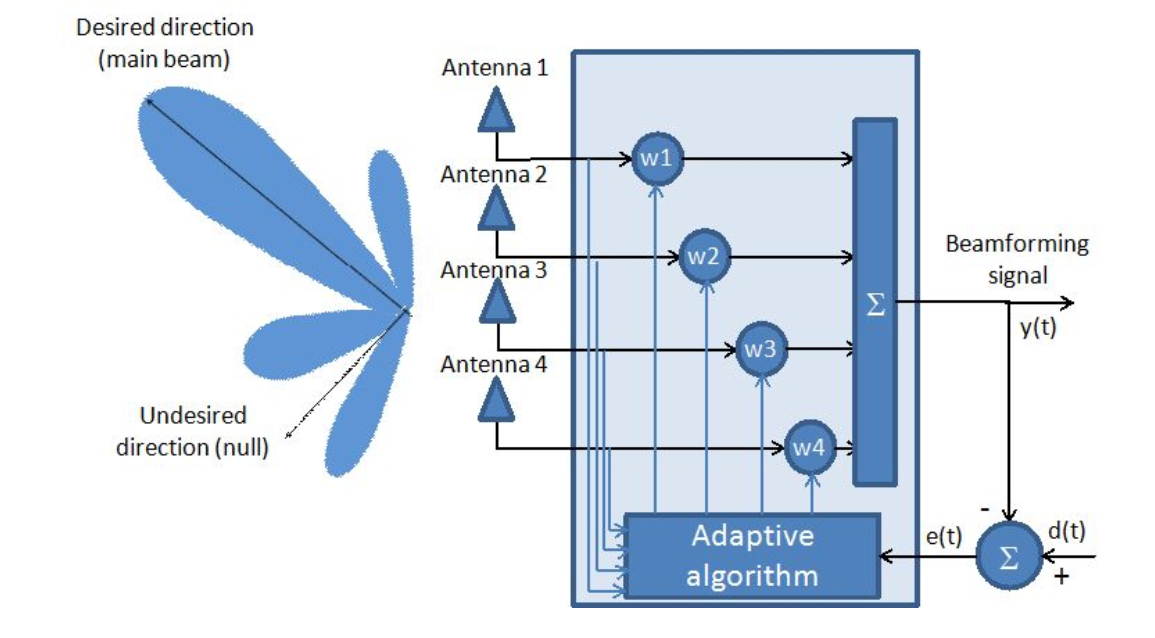
Fig. 1. Sistem antena adaptif.

Seperti dapat dilihat dari gambar, susunan antena dianggap sebagai filter adaptif.

Sebenarnya, menemukan vektor koefisien optimal ( $\ mathbf {w} _ {opt}$ ) adalah tugas utama array antena adaptif dari sudut pandang matematika.

Awalnya, kita tidak tahu dari arah mana sinyal datang dan berapa banyak dari mereka. Untuk menyelesaikan kontradiksi ini kita akan menggunakan algoritma MUSIC, sebuah algoritma untuk memperkirakan frekuensi spasial dengan resolusi tinggi.

Simulasi sinyal yang diterima

Kami dapat menyajikan model sinyal yang diterima melalui rumus:

$\ mathbf {X} = \ mathbf {A} \ mathbf {S} + \ mathbf {N}$

dimana $\ mathbf {A} = [\ mathbf {a} (\ theta_1) \ quad \ mathbf {a} (\ theta_2) \ quad ... \ quad \ mathbf {a} (\ theta_d)]$ - matriks vektor pemindaian (vektor kemudi) dari susunan antena ( $a_i = \ exp (-j \ mu m_i)$ , $m = 0, 1 ... (M-1)$ , $M.$ - jumlah elemen array antena, $d$ - jumlah sumber gelombang EM, $\ theta$ - miringkan arah kedatangan gelombang EM), $\ mathbf {S}$ - matriks karakter yang dikirimkan, dan $\ mathbf {N}$ - Matriks noise tambahan.

Fig. 2. Array antena linear omnidirectional (ULAA - array anntenna linear seragam) [1, hal. 32].

Mari kita memikirkan kembali formula ini dengan cara "sehari-hari": di grid kita, kita mendapatkan beberapa "kekacauan" dari berbagai sinyal, yang kita tandai dengan $\ mathbf {X}$ . Kami tidak secara eksplisit menerima informasi tentang jumlah sumber dan arah, namun, informasi tentang ini tetap terkandung dalam sinyal yang diterima.

Kami mulai mencari!

Untuk melakukan ini, mereka biasanya melanjutkan ke manipulasi tidak dengan matriks dari sinyal kompleks yang diamplitasikan sendiri, tetapi dengan kovarian mereka (yaitu, pada dasarnya, dengan kekuatan):

$\ mathbf {R} _ {xx} = \ mathbf {X} \ mathbf {X} ^ H = \ mathbf {A} \ mathbf {R} _ {ss} \ mathbf {A} ^ H + \ mathbf {R} _ {nn}$

Ketentuan

Kami memperkenalkan kondisi penting untuk dipertimbangkan: batas resolusi sudut Rayleigh:

$sin (\ theta_R) = \ frac {\ lambda} {D}$

dimana $D = M \ Delta$ Apakah panjang kisi linear.

Kami mendefinisikan kembali sudut kedatangan gelombang elektromagnetik melalui konsep frekuensi spasial:

$\ mu_R = \ frac {2 \ pi} {\ lambda} \ Delta dosa (\ theta_R) = \ frac {2 \ pi} {\ lambda} \ Delta \ frac {\ lambda} {\ Delta M} = \ frac { 2 \ pi} {M}$

dimana $\ mu_R$ - ada lebar standar dari lobus utama balok ( beamwidth standar ).

Untuk memeriksa seberapa efektif metode kami dan dalam kondisi apa, kami memperkenalkan beberapa nilai yang diberikan untuk pemisahan sudut:

$\ mu_1 = - \ mu_R, \ quad \ mu_2 = 0, \ quad \ mu_3 = \ mu_R \ quad$ - pembagian menjadi satu lebar balok;
$\ mu_1 = -0.5 \ mu_R, \ quad \ mu_2 = 0, \ quad \ mu_3 = 0,5 \ mu_R \ quad$ - Pembagian menjadi satu lebar balok kedua;
$\ mu_1 = -0,3 \ mu_R, \ quad \ mu_2 = 0, \ quad \ mu_3 = 0,3 \ mu_R \ quad$ - Pembagian menjadi tiga persepuluh dari lebar balok.

Tentukan parameter input:

 M = 10 #    () SNR = 10 #  - (dB) d = 3 #     N = 50 #  "" (snapshots) S = ( np.sign(np.random.randn(d,N)) + 1j * np.sign(np.random.randn(d,N)) ) / np.sqrt(2) # QPSK W = ( np.random.randn(M,N) + 1j * np.random.randn(M,N) ) / np.sqrt(2) * 10**(-SNR/20) # AWGN #  : # sqrt(N0/2)*(G1 + jG2), #  G1  G2 -   . # .. Es( )  QPSK  1 ,    (noise spectral density): # N0 = (Es/N)^(-1) = SNR^(-1) [] (   ,  SNR = Es/N0); #    : # SNR_dB = 10log10(SNR) => N0_dB = -10log10(SNR) = -SNR_dB []; #    SNR    (..  ),   : # SNR = 10^(SNR_dB/10) => sqrt(N0) = (10^(-SNR_dB/10))^(1/2) = 10^(-SNR_dB/20) mu_R = 2*np.pi / M

Sedikit teori tentang metode itu sendiri

Pertama-tama, kami mencatat bahwa leluhur dari metode MUSIK adalah metode Pisarenko (1973). Masalah yang dipertimbangkan dari metode Pisarenko adalah memperkirakan frekuensi jumlah eksponensial kompleks dalam white noise. V.F. Pisarenko menunjukkan bahwa frekuensi dapat ditemukan dari vektor eigen yang sesuai dengan nilai eigen minimum dari matriks autokorelasi. Selanjutnya, metode ini menjadi kasus khusus dari metode MUSIC. [2, hlm. 459]

Schmidt dan rekan-rekannya mengusulkan Algoritma Klasifikasi Beberapa Sinyal (MUSIK) pada tahun 1979 [4]. Pendekatan utama dari algoritma ini adalah untuk menguraikan matriks kovarians dari sinyal yang diterima menjadi nilai eigen. Karena algoritma ini memperhitungkan kebisingan yang tidak berkorelasi, matriks kovarian yang dihasilkan memiliki bentuk diagonal. Di sini, sinyal dan kebisingan subruang dihitung menggunakan aljabar linier, dan saling orthogonal. Oleh karena itu, algoritma ini menggunakan properti orthogonality untuk mengekstraksi subruang sinyal dan noise [5].

Algoritma MUSIC yang digeneralisasi dapat didefinisikan sebagai berikut:

Temukan matriks kovarians $\ mathbf {R} _ {xx}$
Temukan vektor eigen melalui EVD atau algoritma numerik lain yang sesuai:

$\ mathbf {R} _ {xx} = \ mathbf {U} \ mathbf {\ Lambda} \ mathbf {U} ^ H \ qquad (1)$

Temukan spektrum pseudo (mengapa dengan pseudo awalan, kita akan bahas di bawah) MUSIK melalui rumus berikut:

$P_ {MU} (e ^ {j \ omega}) = \ frac {1} {\ sum \ limit_ {i = d + 1} ^ {M} | \ mathbf {a} ^ H \ mathbf {u} _i | ^ 2} \ qquad (2)$

dimana $\ mathbf {a} = \ begin {bmatrix} e ^ {j0 \ omega} & e ^ {j1 \ omega} & e ^ {j2 \ omega} & ... & e ^ {j (M-1) \ omega } \ end {bmatrix} ^ T$ Apakah vektor eksponensial untuk frekuensi ω terletak pada rentang tertentu, dan $\ mathbf {u} _i$ - vektor eigen ke-i (vektor eigen) dari matriks kovarians (1) yang sesuai dengan subruang kebisingan dari matriks (1) - maka indeksasi dengan $d +1$ ( $d$ Apakah pangkat matriks (1)).

Untuk kejelasan yang lebih besar, cobalah menjalankan skrip MATLAB yang sesuai dengan referensi . Perhatikan dua poin utama:
alih-alih menghitung kuadrat dari norma kedua dalam penyebut (2), penulis menerapkan algoritma FFT ke vektor eigen, yang memfasilitasi pemodelan dengan menggunakan fungsi bawaan dan, secara umum, tidak bertentangan dengan teori dari sudut pandang matematika;
matriks kovarians dihitung melalui matriks konvolusional, pendekatan yang berbeda ditunjukkan di atas untuk memperkirakan frekuensi spasial.

Seperti yang Anda tebak dari namanya, MUSIC juga merupakan metode klasik untuk memperkirakan arah penerimaan dengan resolusi tinggi. Algoritma untuk menghitung pseudo-spektra dalam konteks ini diberikan di bawah ini:

kami menemukan matriks kovarians dari sinyal yang diterima;
temukan subruang nol $\ mathbf {U} _0$ :

$\ mathbf {U} = [\ mathbf {U} _s \ quad \ mathbf {U} _0]$

pilih beberapa rentang pencarian:

$a (\ mu) = \ begin {bmatrix} e ^ {j0 \ mu_1} & ... & e ^ {j0 \ mu_Q} \\ ... & ... & ... \\ e ^ {j ( M-1) \ mu_1} & ... & e ^ {j (M-1) \ mu_Q} \ end {bmatrix}$

dimana $\ mu = - \ frac {2 \ pi f_c} {c} \ Delta sin \ theta = - \ frac {2 \ pi} {\ lambda} \ Delta sin \ theta$

hitung spektrum pseudo:

$P_ {MU} (\ theta) = \ frac {\ mathbf {a} ^ H (\ theta) \ mathbf {a} (\ theta)} {\ mathbf {a} ^ H (\ theta) \ mathbf {U} _0 \ mathbf {U} _0 ^ H \ mathbf {a} (\ theta)}$

Hubungan antara analisis spektral dan analisis sudut kedatangan (DoA - arah kedatangan) gelombang EM dijelaskan pada tabel 1.

Tabel 1 Komunikasi antara aplikasi MUSIC : Pemrosesan array sinyal dan pencarian Harmonic [6].

Variabel	Pemrosesan Array Sinyal	Pencarian Harmonis
$M.$	Jumlah sensor	Jumlah periode waktu
$N$	Jumlah periode waktu	Jumlah percobaan
$d$	Jumlah front gelombang	Jumlah komponen kompleks
$\ mu$	Frekuensi spasial	Frekuensi yang dinormalisasi

Secara umum, proses penerimaan melalui array (grating) dapat dibandingkan dengan proses diskritisasi klasik, karena pada kenyataannya, setiap sensor, yang menerima gelombang dengan penundaan fase tertentu (yaitu, dengan penundaan waktu tertentu), melakukan fungsi pulsa delta sampel. Jumlah realisasi (percobaan) analisis spektral klasik akan sesuai dengan jumlah segmen waktu (foto). Setiap sumber akan memiliki muka gelombang sendiri, yang setara dengan jumlah sinusoid unik dari sinyal dalam kasus analisis spektral.

Dan sekarang kembali ke saat menghitung vektor eigen. Kami sudah disebutkan di atas vektor itu $a (\ theta_i) \ epsilon A$ dimana $i = 1,2, .., d$ bersifat ortogonal ke subruang kebisingan dari matriks kovarians, yaitu .:

$a (\ theta_i) ^ TU_0 = 0 ^ T$

Sebenarnya, kita melihat sistem persamaan, pemecahan yang dapat kita temukan akar - vektor eigen. Metode seperti itu, berbeda dengan algoritma numerik (yang, seperti yang kami sebutkan di atas, berlaku untuk EVD), memungkinkan seseorang untuk mendapatkan nilai eigen yang nyata daripada perkiraan. Itulah sebabnya pendekatan ini memungkinkan kita untuk mendapatkan bukan pseudospectrum, tetapi spektrum. Ide yang sama membentuk dasar dari algoritma Root MUSIC .

Pemodelan

Fuf! Akhirnya, semua formula dijelaskan dan agak dijelaskan. Kita bisa memulai pemodelan.

 cases = [[-1., 0, 1.], [-0.5, 0, 0.5], [-0.3, 0, 0.3],] for idxm, c in enumerate(cases): #   ( ): mu_1 = c[0]*mu_R mu_2 = c[1]*mu_R mu_3 = c[2]*mu_R #   a_1 = np.exp(1j*mu_1*np.arange(M)) a_2 = np.exp(1j*mu_2*np.arange(M)) a_3 = np.exp(1j*mu_3*np.arange(M)) A = (np.array([a_1, a_2, a_3])).T #    X = np.dot(A,S) + W #    R = np.dot(X,np.matrix(X).H) U, Sigma, Vh = np.linalg.svd(X, full_matrices=True) U_0 = U[:,d:] #   thetas = np.arange(-90,91)*(np.pi/180) #   mus = np.pi*np.sin(thetas) #    a = np.empty((M, len(thetas)), dtype = complex) for idx, mu in enumerate(mus): a[:,idx] = np.exp(1j*mu*np.arange(M)) # MVDR: S_MVDR = np.empty(len(thetas), dtype = complex) for idx in range(np.shape(a)[1]): a_idx = (a[:, idx]).reshape((M, 1)) S_MVDR[idx] = 1 / (np.dot(np.matrix(a_idx).H, np.dot(np.linalg.pinv(R),a_idx))) # MUSIC: S_MUSIC = np.empty(len(thetas), dtype = complex) for idx in range(np.shape(a)[1]): a_idx = (a[:, idx]).reshape((M, 1)) S_MUSIC[idx] = np.dot(np.matrix(a_idx).H,a_idx)\ / (np.dot(np.matrix(a_idx).H, np.dot(U_0,np.dot(np.matrix(U_0).H,a_idx)))) plt.subplots(figsize=(10, 5), dpi=150) plt.semilogy(thetas*(180/np.pi), np.real( (S_MVDR / max(S_MVDR))), color='green', label='MVDR') plt.semilogy(thetas*(180/np.pi), np.real((S_MUSIC/ max(S_MUSIC))), color='red', label='MUSIC') plt.grid(color='r', linestyle='-', linewidth=0.2) plt.xlabel('Azimuth angles θ (degrees)') plt.ylabel('Power (pseudo)spectrum (normalized)') plt.legend() plt.title('Case #'+str(idxm+1)) plt.show()

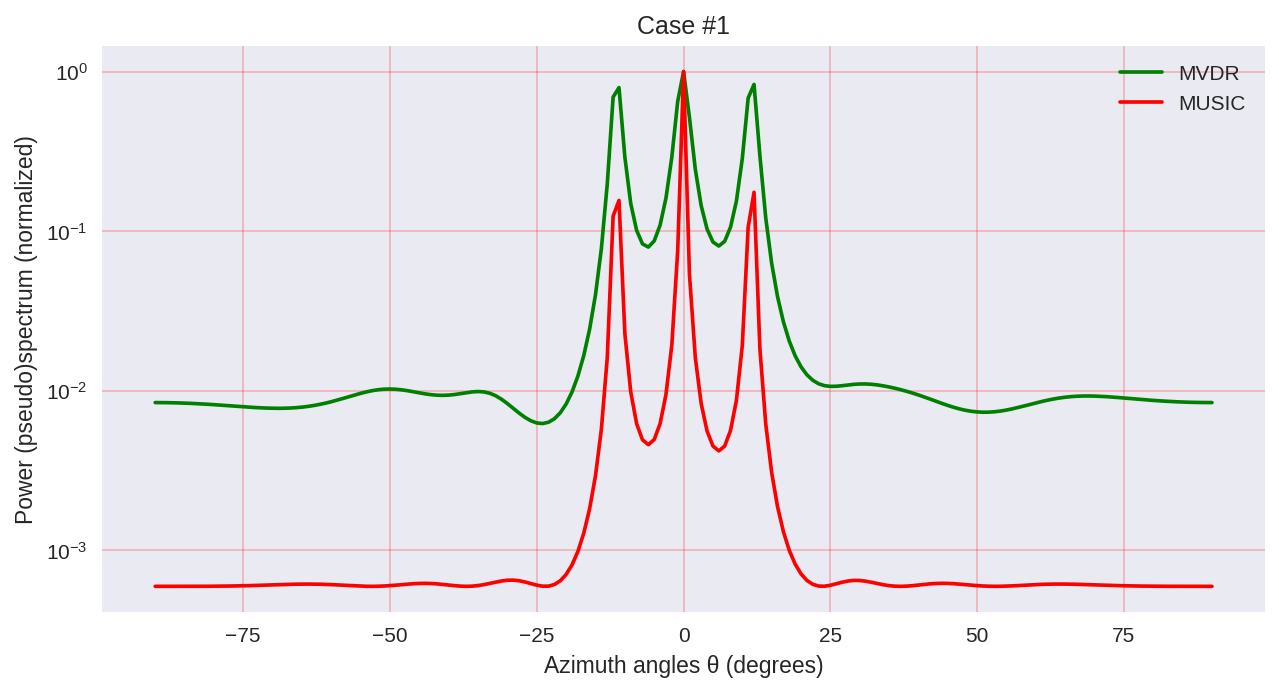
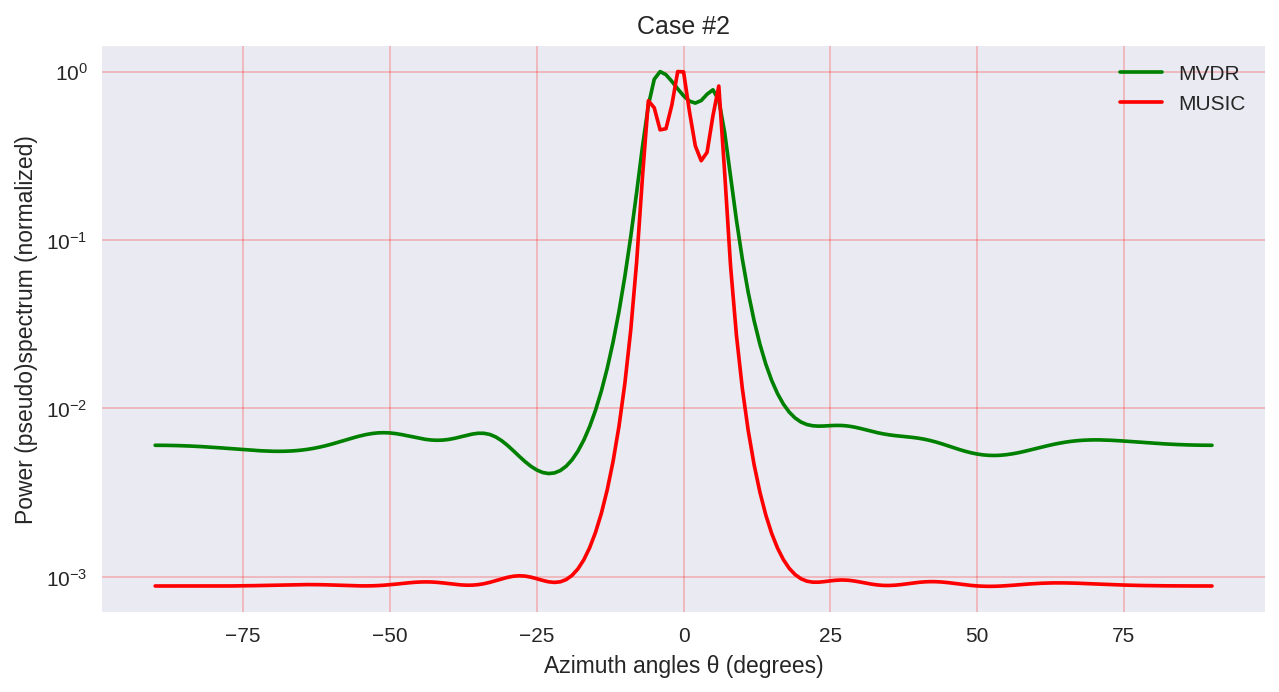
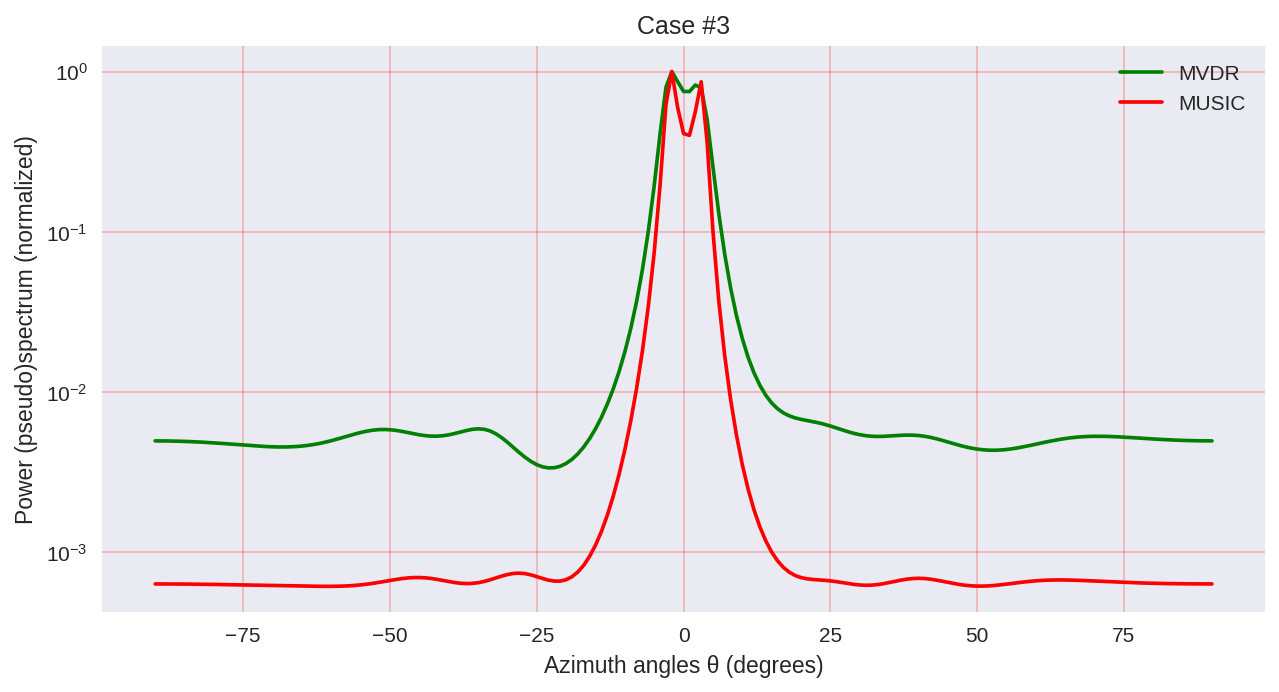
Seperti yang dapat kita lihat, MUSIC memiliki resolusi yang lebih tinggi dan memungkinkan untuk mencapai, secara umum, hasil yang lebih baik daripada, misalnya, MVDR memungkinkan - perwakilan yang sama dari metode parametrik analisis spektral.

Namun, harus diingat bahwa ketika menggunakan MUSIC kita menggunakan algoritma yang lebih mahal secara komputasi, seperti EVD atau SVD, yang harganya terjangkau untuk akurasi yang lebih tinggi.

Hal-hal seperti itu.

Daftar literatur yang digunakan:

Haykin, Simon, dan KJ Ray Liu. Buku pegangan tentang pemrosesan array dan jaringan sensor. Vol. 63. John Wiley & Sons, 2010. hlm. 102-107
Hayes MH Statistik pemrosesan sinyal digital dan pemodelan. - John Wiley & Sons, 2009.
Haykin, Simon S. Adaptive filter theory. Pearson Education India, 2008. hlm. 422-427
Richmond, Christ D. "Algoritma Capon berarti ambang batas kesalahan prediksi SNR dan probabilitas resolusi." Transaksi IEEE pada Pemrosesan Sinyal 53.8 (2005): 2748-2764.
SKP Gupta, MUSIC, dan algoritme MUSIC yang ditingkatkan untuk memperkirakan kedatangan, IEEE, 2015.
Kuliah Profesor Martin Haardt ( array array )

Kami memodelkan algoritma MUSIK untuk menentukan arah kedatangan gelombang elektromagnetik